旋转式合成孔径雷达干涉成像方法

杨 科， 廖桂生， 徐 青

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

笔者根据ROSAR系统能够快速重访同一场景的特点，并结合直升机等旋翼飞行器易于悬停的特性，建立了ROSAR 的干涉成像模型．在该模型下，成像平台首先保持在某一高度上完成场景的一次观测，然后上升至另一高度完成场景的二次观测，经过两次或者多次观测可以获得多组ROSAR数据，通过对这些数据进行干涉处理获得场景的高程信息．在实际的数据采集过程中，由于受强风、对流等天气影响，同一系统平台在不同高度上存在旋转轴偏移问题．轴偏移将会引起天线与场景之间的距离变化，而在ROSAR模式中，由于受到物理结构的限制，不同斜距对应的合成孔径大小存在差异．因此，轴偏移会导致同一场景目标的方位带宽有所变化，同时轴偏移也会引起干涉相位发生变化，使得高程信息无法正确获取．为了使不同高度的转轴位置相互重合，同时保障转轴位置和场景位置的相对关系，笔者采用转轴和场景整体平移的方法，将轴偏移等效为场景位置移动，进而分析场景位置变化对方位带宽和干涉相位的影响，获取斜距差和偏移量的关系式，最后通过构建补偿函数来消除轴偏移的影响．

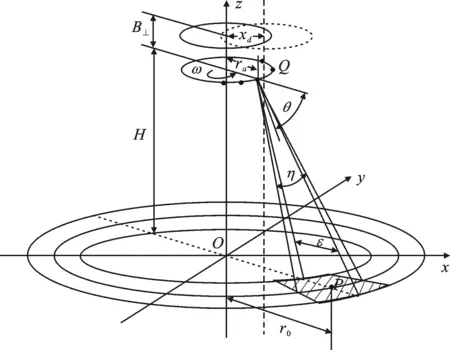
图1 ROSAR干涉模型示意图

1 ROSAR干涉模型

如图1所示，雷达平台距地面的高度为H，平台上的天线以角速度ω作匀速圆周运动，并指向背离转轴方向，对周围场景进行圆环形照射．定义天线到转轴中心的垂直距离(旋转半径)为ra，俯仰角为θ，俯仰向波束宽度为ε，方位角为0°(天线照射方向垂直于天线速度方向)，方位向波束宽度为η．考虑到天线作圆周运动，为了便于分析和计算，文中采用圆柱坐标系(r，φ，z)．不失一般性，假设天线旋转至x轴平行位置时，旋转角定义为0°．旋转至任意位置Q时，旋转角为ωta，则天线位置为(ra，ωta，H)．假设点目标P的位置为(r0，φ0，z0)，r0表示点目标的地面距离(地距)，φ0表示点目标的方位向位置，z0表示点目标的高度，则天线至点目标的斜距表达式为

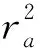
(1)

假设雷达发射线性调频脉冲信号p(t)=rect(t/Tp) exp(j2πfct+jπγt2)，Tp为发射脉冲宽度，fc为发射信号载频，γ为信号调频率．点目标回波经过基频变换，在距离快时间-方位慢时间域 (tr-ta域)可表示为

(2)

其中，λ是发射信号波长．

利用已有的二维ROSAR成像算法[2，7-8]，对原始回波数据S0进行二维匹配成像，可得单幅ROSAR图像为

(3)

其中，A1表示二维成像后的幅度，Br表示发射信号带宽，Ba表示方位向带宽，α表示天线至点目标的最短斜距，α= ((ra-r0)2+(H-z0)2)1/2．

当平台垂直上升至另一高度H+B⊥时，对场景进行第2次观测，如图1所示，可利用二维成像算法获得第二幅ROSAR图像．通过对两幅图像进行干涉处理可获得场景的高程信息，即能实现ROSAR干涉成像的目的．

初中数学学科涉及的知识范围广，难度大，平时还有许多考试，需要时间进行复习，因此，对教师的教学进度有一定要求。这使得教师的教学过程往往以提高课堂教学效率为目标，在培养学生独立思考能力方面就会流于表面，只注重形式化的过场，而没有把培养学生独立思考能力的教学活动真正落到实处，学生无法理解独立思考的本质，也就无法提高自身的独立思考能力。

2 轴偏移影响及补偿方法

在实际情况中，由于受到周围环境影响，不同高度的旋转轴中心可能存在偏移，如图1中的虚线所示，两轴之间的偏移量为xd．为了方便讨论，图中假设转轴偏移方向与x轴平行，这一假设不影响模型实质描述．要使第2次数据录取坐标与第1次的相同，需对第2个转轴中心进行 (-xd，0，0)的位置校正．由于转轴位置和场景位置是相对的，为了满足转轴与场景的位置相对不变，需同时对照射场景进行整体移动．原场景内的点目标P位置为(r0，φ0，z0)，假设移动后的点目标P′位置为(roffset，φoffset，z0)，P与P′的关系为

整理式(4)和式(5)可得新的位置参数为

在新的坐标位置下，式(3)中的斜距位置α、方位向位置φ0以及相位大小 -4πα/λ发生改变，其中，新的斜距大小α′= ((ra-roffset)2+ (H-z0)2)1/2．同时，由于ROSAR的特殊几何结构，在新的坐标中方位向带宽Ba也有相应的变化，导致干涉图像之间的相关性下降．以下具体分析转轴偏移对方位带宽和干涉相位的影响．

2.1 对方位带宽的影响

在传统的线性SAR成像系统中，多普勒调频率随斜距的增加而减少，但是合成孔径时间随斜距的增加而增加，因此，不同斜距的方位带宽是相同的[9-10]．而在ROSAR系统中，由于物理结构的限制，合成孔径时间不能随斜距的增长而线性增长，进而导致不同斜距的方位带宽不同．以下将基于ROSAR的方位向调频率和合成孔径时间的计算，对方位带宽进行推导，进而分析转轴偏移对方位带宽的影响．

利用匹配函数对原始回波数据S0进行距离向匹配，可得

(8)

其中，A2表示距离向匹配后的幅度．

对式(8)中的相位进行二次求导，可得方位向调频率为

(9)

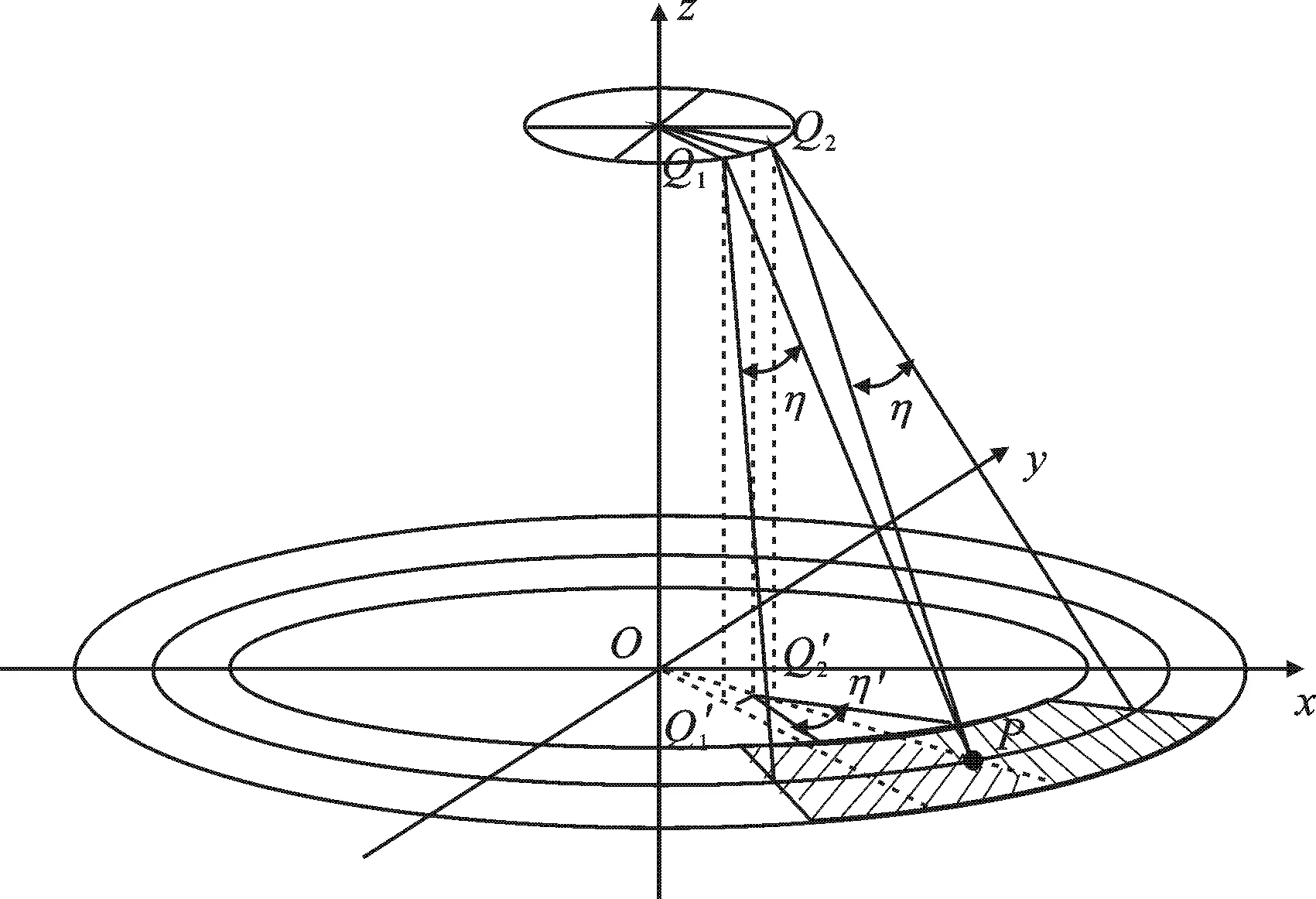
图2 ROSAR合成孔径示意图

(10)

其中，η′为方位向波束宽度η在水平面上的投影．对于高度位置为z0的点目标，假设俯仰角为θz0，根据几何关系可得 cosθz0= (r0-ra)/α，从而可得η′和η的关系表达式为

tan(η′/2)=tan(η/2)/cosθz0．

(11)

文献[11]给出了二维场景的合成孔径长度表达式，在不考虑平台高度H和点目标高度z0的情况下，笔者将三维场景简化为二维场景，令η′=η，式(10)简化为S=ηra(1-ra/r0)，此时该式与文献[11]中的表达形式相一致．

假设T为方位向有效合成孔径时间，则时间T与孔径S的关系可表示为

ωT=S/ra．

(12)

根据式(9)的方位向调频率Ka及式(10)～式(12)所得的合成时间T，可得方位向带宽为

Ba=|KaT|=2βωη′(1-ra/r0)/(λα) ．

(13)

由式(13)可知，方位带宽Ba随着r0的变化而变化，而转轴偏移可以等效于r0的变化，进而引起Ba的变化．根据文献[12-13]可知，方位带宽的差异将会导致信号去相关，进而使得干涉相位的等效噪声增加．如果转轴偏移引起的方位带宽变化较大，在预处理的过程中需要对原图像进行方位预滤波，从而保证最终的干涉成像结果．

2.2 对干涉相位的影响及补偿方法

转轴偏移对图像相位也会产生影响，即式(3)中相位 exp(-j4πα/λ) 变为 exp(-j4πα′/λ)．以下分析两者相位差 exp(-j4πΔα/λ) 与转轴偏移量xd的关系表达式，其中斜距差表示为 Δα=α′-α．

将变化后的地距roffset表示为r0+Δr0，并对斜距α′进行泰勒级数展开，可得

(14)

式(14)中二次及二次以上高次项为极小量，在只保留一次项的情况下可得斜距差Δα= (r0-ra)Δr0/α．而地距差可表示为 Δr0=roffset-r0，重新改写式(6)，并对其进行泰勒级数展开，可得

(15)

忽略式(15)中的二次及二次以上极小量，可得Δr0=-cosφ0xd．结合式(14)所得结果，以Δr0为中间变量，可得斜距差Δα与转轴偏移量xd的关系式为

Δα=[-(r0-ra)/α] cosφ0xd．

(16)

由以上分析可知，旋转中心轴的偏移导致图像增加了一个附加相位 exp(-j4πΔα/λ)，其中Δα如式(16)所示．通过干涉手段获取场景的高程信息，对干涉相位的精确性有极高的要求．为了正确恢复场景高程信息，需要对上述附加相位进行补偿．补偿函数为

(17)

对两幅ROSAR图像进行配准处理，并通过复共轭相乘获取原始干涉相位．该相位包含了轴偏移所引起的附加相位．在去平地相位之前，利用式(17)所示函数与原始相位进行相乘，可实现附加相位校正．接着通过去平地相位、相位解缠绕及高度换算等处理，最终可获得ROSAR场景高程信息．

3 仿真实验

ROSAR系统的主要仿真参数如下: 平台高度 1 000 m，旋转半径 1.5 m，地距变化范围 1 100 m～ 2 300 m，俯仰角60°，信号发射波长 0.03 m．图3给出了旋转轴偏移对方位带宽的影响．通常情况下旋转轴受环境影响存在数米到数十米的偏移量，图3考虑极大偏移情况，选取偏移量为 100 m．图3(a)以场景目标的方位位置φ0为参变量，给了轴偏移前后的方位带宽差ΔBa随地距r0的变化曲线．由图可知，轴偏移会引起方位带宽发生变化(即存在方位带宽差)，轴偏移方向上 (φ0=0°，实线所示)的目标带宽差变化较大，远离轴偏移方向 (φ0=90°，虚线所示)的目标带宽差变化较小，但是对于各方位位置上的目标来说，方位带宽变化都为较小量．图3(b)给出了某一点目标在轴偏移前后的方位带宽截面图，点目标的具体位置为方位向φ0=0°、地距向r0=1 733 m，由图可知，两者的方位带宽基本上是一致的．综上所述，轴偏移会导致方位带宽发生变化，但是该变化量较小，可忽略其影响．

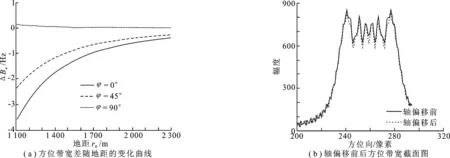
图3 方位带宽影响分析

图4给出了旋转轴偏移所引起的干涉相位影响．图4(a)为不同平台高度的两幅ROSAR图像干涉相位图，两幅图像在产生干涉相位前已经过图像配准处理，平台1高度为 1 000 m，平台2高度为 1 001 m，假设平台1的轴位置为参考位置，平台2相对平台1水平偏移 2 m，其它参数如上述所示．平台2的轴位置偏移导致干涉相位中存在一个附加相位，图4(b)给出了上述偏移所产生的附加相位图，该相位将会影响最终的高程信息获取，为此需要对这一附加相位进行补偿，补偿结果如4(c)所示．图4(c)中包含平地相位，对其进行去平地相位处理，并进行相位解缠绕及高度换算，最终可得到如图4(d)所示的场景高程图．

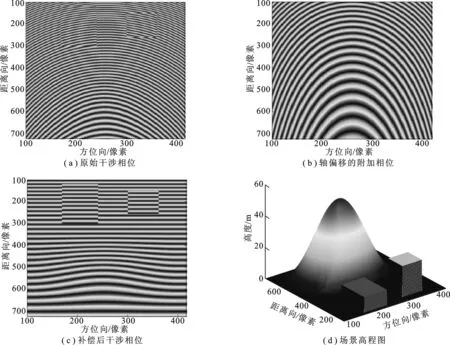
图4 干涉成像结果

4 结 束 语

笔者构建了ROSAR干涉成像模型，分析了不同高度系统平台的轴偏移问题．通过分析发现，轴偏移会影响方位带宽和干涉相位．实验仿真表明，轴偏移导致ROSAR方位带宽产生变化，但是该变化量较小，在干涉处理过程中可以忽略上述影响．轴偏移对干涉相位产生影响，使得图像有一个附加相位，该相位影响较大，仿真实验在去平地相位之前对该相位进行了校正，获得较好的补偿效果．最后，经过解缠绕及高度换算，获得场景的三维高程图．

[1] Jeon M, Kim Y S. Migration Technique for Rotor Synthetic Aperture Radar [J]. Electronics Letters, 1997, 33(7): 630-631.

[2] Lee H, Cho S J, Kim K E. A Ground-based Arc-scanning Synthetic Aperture Radar (arc-SAR) System and Focusing Algorithms [C]//IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2010: 3490-3493.

[3] Ali F, Urban A, Vossiek M. A Short Range Synthetic Aperture Imaging Radar with Rotating Antenna [J]. International Journal of Electronics and Telecommunications, 2011, 57(1): 97-102.

[4] Zhang Jun. The Static Small Object Detection Based on Ground-based Arc SAR [C]//International Conference on Microwave and Millimeter Wave Technology. Piscataway: IEEE, 2012: 1489-1492.

[5] Ghasr M T, Pommerenke D, Case J T, et al. Rapid Rotary Scanner and Portable Coherent Wideband Q-band Transceiver for High-resolution Millimeter-wave Imaging Applications [J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(1): 186-197.

[6] 廖轶, 周松, 邢孟道, 等. 一种基于级数反演的机载圆迹环扫SAR成像算法 [J]. 电子与信息学报, 2012, 34(11): 2587-2593.

Liao Yi, Zhou Song, Xing Mengdao, et al. An Imaging Algorithm for Airborne Circular Scanning SAR Bbased on the Method of Series Reversion [J]. Journal of Electronics & Information Technology, 2012, 34(11): 2587-2593.

[7] Bara M, Sagués L, Paniagua F, et al. High-speed Focusing Algorithm for Circular Synthetic Aperture Radar (C-SAR) [J]. Electronics Letters, 2000, 36(9): 828-830.

[8] 孙兵, 周荫清, 陈杰, 等. 广域观测圆轨迹环扫SAR成像模式研究 [J]. 电子与信息学报, 2008, 30(12): 2805-2808.

Sun Bing, Zhou Yinqing, Chen Jie, et al. Operation Mode of Circular Trace Scanning SAR for Wide Observation [J]. Journal of Electronics & Information Technology, 2008, 30(12): 2805-2808.

[9] 侯育星, 张磊, 徐刚, 等. 脉冲相位编码信号大测绘带合成孔径雷达成像 [J]. 西安电子科技大学学报, 2012, 39(5): 54-60.

Hou Yuxing, Zhang Lei, Xu Gang, et al. Wide Swath SAR Imaging with Pulse-phase-codes [J]. Journal of Xidian University, 2012, 39(5): 54-60.

[10] 梁毅, 王虹现, 邢孟道, 等. 同航线双基调频连续波SAR改进距离徙动算法 [J]. 西安电子科技大学学报, 2011, 38(1): 71-79.

Liang Yi, Wang Hongxian, Xing Mengdao, et al. Modified RMA for the Tandem Bistatic FMCW SAR with Frequency Non-linearity Correction [J]. Journal of Xidian University, 2011, 38(1): 71-79.

[11] Kreitmair-Steck W, Braun G. Heliradar Technology for Helicopter Allweather Operations [C]//Proceedings of SPIE-Radar Sensor Technology Ⅱ. Bellingham: SPIE, 1997: 28-38.

[12] 郭交, 李真芳, 刘艳阳, 等.一种基于相干性本质的InSAR方位向预滤波方法 [J]. 电子学报, 2012, 40(3): 417-421.

Guo Jiao, Li Zhenfang, Liu Yanyang, et al. An Improved Method for InSAR Azimuth Prefiltering Based on Coherence Principle [J]. Acta Electronica Sinica, 2012, 40(3): 417-421.

[13] Wang R, Deng Y K, Loffeld O, et al. Focusing Bistatic SAR Data in Double Sliding Spotlight Mode with TerraSAR-X and PAMIR Based on Azimuth Chirp Filtering [C]//9the European Conference on Synthetic Aperture Radar. Piscataway: IEEE, 2012: 772-775.