二维脉内扫描高信噪比高分辨大测绘带成像

张佳佳， 周 芳， 孙光才， 邢孟道， 保 铮

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

受最小天线面积的限制，星载合成孔径雷达(Synthetic Aperture Radar， SAR)成像应用中，高分辨与宽测绘带构成一对矛盾[1]．为了突破高分辨率和大测绘带之间的矛盾，近年来国内外学者对高分辨大测绘带(High-Resolution Wide-Swath， HRWS)成像模式进行了大量的研究[2-12]．文献[3]将大天线沿距离向分割获得沿距离向线阵，利用接收端数字波束形成(Digital Beam Forming， DBF)解距离模糊实现宽测绘带．文献[4-7]将大天线沿航向分割为多个子孔径，由其中1个子孔径发射宽波束，其他所有子孔径同时接收回波，以低脉冲重复频率(PRF)获得宽测绘带．它们的共同点是都采用短天线发射宽波束，天线发射面积较小，回波信噪比低．从雷达方程可知，回波的信噪比会随着测绘场景的增大和分辨率的提高而降低．信噪比不仅是衡量SAR成像效果本身的一个重要指标，还直接影响着运动目标检测性能、定位精度以及图像干涉测高的精度等性能．因此，需要研究能够改善信噪比的HRWS成像模式．

文献[8]为了提高回波信噪比，提出了利用沿航向子孔径解方位模糊实现HRWS成像，面阵俯仰维多个子孔径相干积累提高回波信噪比．然而该系统是通过单孔径发射、面阵接收，发射孔径面积小．文献[9-10]提出了在发射端采用多维波形编码并结合DBF技术，利用整个方位维阵列发射方位维窄波束，并在1个脉冲发射时间内分时进行方位维脉内扫描．该模式增加了天线发射增益，改善了信噪比，但其仅采用面阵中的某一行方位维阵列发射信号，发射通道利用率不高．文献[11]提出了一种通过俯仰维脉内扫描和低PRF获得大测绘带，采用面阵接收回波，利用两维自由度解距离和方位模糊的HRWS成像模式．该模式利用长距离阵列发射俯仰维的窄波束，提高了天线发射面积，但其仅采用某一列俯仰维阵列发射信号，发射通道利用率同样不高．

笔者提出了一种基于俯仰-方位二维脉内扫描的SAR成像模式及相应的二维解模糊算法，利用了整个面阵资源发射二维窄波束，实现了面阵全孔径发射和接收，充分提高了发射通道的利用率，有效提高了高分辨大测绘带成像系统的信噪比．

图1 二维脉内扫描SAR系统模型

1 系统工作模型

假设系统在1个脉冲发射时间内分时发射多个子脉冲，利用整个面阵天线形成俯仰-方位两维窄波束，通过相位加权技术控制波束指向，使其按照特定的顺序在不同子脉冲时间内扫描不同的俯仰-方位子测绘带，称之为二维脉内扫描．二维脉内扫描SAR工作模式如图1所示．图1中以 2×3 面阵为例，该系统共扫描两个俯仰子测绘带，每个俯仰子测绘带采用3个方位子波束分时扫描，形成3个方位子场景．图1中用数字标出了各子场景的扫描顺序．

由图1所示，二维脉内扫描SAR工作模式控制雷达波束以由远及近的顺序扫描各个俯仰子测绘带，对于每个俯仰子测绘带，都在不同子脉冲时间内以方位子波束按飞行方向从前到后的顺序对其进行扫描．文中也是以由远到近，由前到后的顺序分别对俯仰子测绘带和方位子测绘带进行编号．此时只需要采用稍大于子波束的方位带宽Binst的PRF，即可通过解模糊处理获得无模糊的方位谱，从而大大降低了系统PRF的要求，缓解了高分辨率和大场景之间的矛盾，实现了高分辨大场景成像．

2 系统性能分析

文中提出的二维脉内扫描SAR系统具有多个优点．首先，二维脉内扫描SAR系统通过全阵面发射和接收，有效利用了天线发射和接收面积，能够在其他条件一定的情况下大幅提高信噪比；或在保持一定信噪比的情况下，能显著降低对天线阵元发射功率的要求．其次，二维脉内扫描兼具俯仰和方位维脉内扫描的优点[9-12]，具有灵活的功率分配特性和多距离分辨特性，能够通过调整照射不同俯仰测绘带的发射信号的脉冲时宽和带宽，分别调整不同距离测绘带的信噪比和距离分辨率，以满足成像需要．不过，由于文中提出的二维脉内扫描系统分时发射子波束信号，信号发射总时间和接收同一测绘带的回波所需的时间都与传统SAR的不同，这会导致PRF为一定值时，该系统最大距离测绘带宽度也与传统SAR的不同．另外，虽然采用低PRF会引起积累增益的下降和信噪比的降低，但是文中提出的成像模式通过充分提高发射天线增益，不仅可以弥补这一损失，还能够显著提高信噪比．下面通过与其他HRWS系统的对比，分析二维脉内扫描SAR系统的信噪比性能和最大距离测绘带宽度．

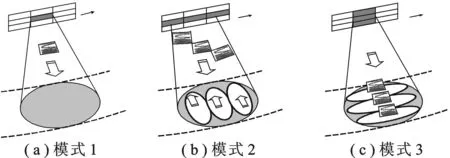
图2 各HRWS成像模式的信号发射模型

2．1 系统信噪比分析

为了说明文中模式的高信噪比特性，将文中模式和文献[8]、文献[9-10]和文献[11]提出的HRWS成像模式(分别记为模式1、模式2和模式3)的回波信噪比进行比较分析．假设系统天线面阵分为U×V个子孔径，每个子孔径面积为A，雷达基本参数一致．令四者以同样的分辨率对同一大测绘带场景进行成像．由雷达方程[11]可知，在其他条件不变的情况下，系统信噪比与发射面积、接收面积成正比．4个模式都是全面阵接收，接收天线的面积均为UVA．因此，4个模式信噪比的差别主要在于发射天线面积不同．图2为模式1～3的信号发射模型的示意图．由图2可见，模式1发射天线面积为A，并假设其信噪比为RSN1．模式2发射天线面积为VA，则其信噪比为 VRSN1．模式3发射天线面积为UA，则其信噪比为URSN1．文中提出的模式发射和接收天线面积都为UVA，因此信噪比为UVRSN1．

由上述分析可见，由于充分利用了面阵资源，提高了发射增益，在其他条件一致的情况下，文中提出的二维脉内扫描SAR成像模式的信噪比是模式1的UV倍，是模式2的U倍，是模式3的V倍，可见，其相对于其他HRWS SAR成像模式，文中模式能够显著提高系统的信噪比．

2．2 系统最大距离测绘带宽度

系统最大距离测绘带宽度是HRWS系统性能的重要指标，这里对该模式的最大距离测绘带宽度进行分析，并与3个HRWS SAR成像模式进行比较．

假设4个模式发射的信号时间宽度均为Tp，模式1可无模糊接收的最大距离测绘带宽度为Wr，其信号发射时间Ttr=Tsys+Tp，Tsys为系统发射信号过程所需要的额外时间，接收全部回波需要接收的窗长度Tre= 2Wr/c+Tp，则有Ttr+Tre= 1/PRF；模式2系统发射时间Ttr，1=Tsys+MTp，接收测绘带宽度为Wr的回波需要时间Tre，1= 2Wr/c+MTp，模式2发射和接收全部回波所需要的时间Tall，1=Ttr，1+Tre，1= 1/PRF+ 2(M-1)Tp，则系统可用作接收回波的时间相对减少了 2(M-1)Tp，即模式2可无模糊接收的最大距离测绘带宽度Wr1=Wr-c(M-1)Tp；模式3系统发射时间Ttr2=Tsys+NTp，接收全部回波需要时间Tre2= 2Wr/c+Tp- (N-1)Tp，系统可用作接收回波的时间不变．因此，模式3可无模糊接收的最大距离测绘带宽度Wr2=Wr．文中提出的系统发射时间Ttr3=Tsys+NMTp，接收全部回波需要时间Tre3= 2Wr/c+MTp- (N-1)MTp，得到该模式可无模糊接收的最大距离测绘带宽度Wr3=Wr-c(M-1)Tp．可见模式1和模式3最大距离测绘带宽度相同，而模式2的最大距离测绘带宽度和文中提出系统的相同，且小于模式1和模式3的最大距离测绘带宽度．

3 回波信号模型

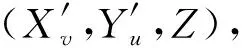
假设系统发射线性调频信号，共有N个俯仰子测绘带，用M个方位子波束扫描每个俯仰子测绘带，扫描同一个俯仰子测绘带的子波束脉冲时宽是相同的，而扫描不同俯仰子测绘带的子波束脉冲时宽可以不同．对于第n个俯仰测绘带中某一散射点Pn(xn，yn，zn)，随着雷达的运动，其在不同的方位时间范围及对应的方位角度内一共被M个不同的方位子波束依次照射．假设散射点Pn被第m个 (m=1，2，…，M)方位子波束照射的方位时间和方位角度范围分别为Tbeam，m和φbeam，m，则第u行、第v列子孔径接收的基带信号可表示为

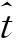
(2)

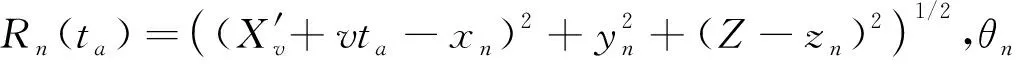
分析信号特点可知，点目标被不同方位子波束照射得到的回波对应着不同多普勒频带，不同多普勒频带之间存在距离错位，所有多普勒频带组成了点目标的完整方位频谱．由于方位采样率PRF仅稍大于子波束瞬时带宽Binst，而远小于方位总带宽MBinst，所以点目标方位频谱会发生混叠，引起M次方位多普勒模糊，方位模糊示意图如图3所示．可见，该点目标在不同方位子波束的回波中对应的方位角φ是不同的，可以从空间上进行区分．而且，虽然同一点目标的不同方位子波束对应的多普勒频带之间会由于发射时间不同发生距离错位，但是不会影响方位模糊特性．只要完成方位解模糊，就可以根据方位频带分离出相应的方位子波束对应的信号．

图3 方位模糊的示意图(以3次模糊为例) 图4 距离模糊的示意图(以2次模糊为例)

距离模糊的示意图如图4所示．图4中存在两种距离模糊，一种是由于脉内扫描不同俯仰子测绘带引起的，这种模糊来自不同的距离子带中的散射点，当分布在第1个到第N个俯仰维子测绘带内的N个散射点P1(x1，y1，z1)～PN(xN，yN，zN)的瞬时距离满足一定条件时，这些散射点的回波同时到达接收端，回波信号会发生混叠，就引起了N次距离模糊．值得注意的是，不同方位子波束信号，距离模糊条件可能不同，对于第m个子波束信号，其处于第n个距离测绘带内的模糊分量的距离满足：

另外一种距离模糊是来自于不同方位子测绘带．当同一距离子测绘带中分布在M个不同方位子测绘带中的散射点满足文献[11]中的距离模糊条件时，就会发生这种距离模糊．跟前一种距离模糊不同，如果通过方位解模糊分离出方位子波束对应的信号，这种距离模糊自然就被分离了．这时每个方位子波束信号中就只存在第1种距离模糊，然后再针对不同方位子波束信号，通过距离DBF就可以完全分离距离模糊．

4 二维解模糊算法

由以上分析可知，二维脉内扫描SAR回波存在N次距离模糊，M次方位模糊．根据阵列信号理论，距离模糊数必须小于俯仰自由度U，方位模糊数必须不大于方位自由度V，即要满足N≤U，M≤V时，才可以进行二维解模糊处理．假设系统自由度满足这个条件，首先利用方位多通道DBF解方位模糊，分离方位子波束信号，再通过俯仰多通道DBF对每个子波束信号解距离模糊得到无模糊的大场景回波信号．

对第u行、第v列的子孔径接收的回波信号进行匹配滤波后，再进行方位傅里叶变换，此时，任意方位频点fa(-PRF/2≤fa≤PRF/2) 处有M个分别来自角度φ1～φM的信号分量模糊在一起，且有φm= arcsin[(2v/λ)(fa+fdc，m)]，m=1，2，…，M，其中，λ为发射波长；fdc，m为不同方位模糊分量的方位频率中心，当M是奇数时，fdc，m= [-(M-1)/2+m-1]PRF；当M是偶数时，fdc，m= (-M/2+m)PRF．因此，含距离和方位二维模糊的信号可表示为

由前节可知，虽然不同方位子波束对应的多普勒频带在距离上存在延时，但是这并不影响方位的时频关系，因此不影响方位解模糊，可以采用类似方位一发多收的方位DBF方法对模糊分量进行分离．第u行的V个方位通道的阵列矢量为

(5)

其中，上标T为转置．构建矩阵为

A(fa)=[a1(fa)，…，am(fa)，…，aM(fa)]V×M．

(6)

则可得方位频率fa+fdc，m对应的权矢量为

wm=A+(fa)em，

(7)

其中，+表示矩阵的伪逆；向量em=[e1，…，eq，…，eM]T，eq=m=1，eq≠m=0，即在对应的方位频率和方位角位置上输出为1，而其他模糊的位置输出为0．提取第u行的V个方位通道的回波信号组成回波矩阵，即

(8)

将式(8)与wm相乘，完成方位向的解模糊处理，分离出fa+fdc，m对应的第m个方位模糊分量为

Su(fa+fdc，m)=Su(fa+fdc，m)wm．

(9)

依次得到各方位模糊分量后，根据图3中不同子波束和方位频谱的对应关系，分离各子波束对应的信号．此时，天线第u行子孔径接收的第m个方位子波束回波信号可以表示为

从式(10)可见，信号方位不再模糊，但每个方位子波束仍存在N次距离模糊．接下来可以利用U个距离自由度解N个距离模糊．对于第m个方位子波束信号，U个距离通道的阵列矢量为

(11)

构建阵列矢量矩阵为B=[β1，…，βn，…，βN]U×N．

(12)

则可得解距离模糊对应的权矢量为vn=B+hn，

(13)

其中，向量hn=[h1，…，hq，…，hN]T，hq=n=1，hq≠n=0，即在对应的下视角位置上输出为1，而其他模糊的位置输出为0．U个俯仰通道的第m个方位子波束回波信号组成的矩阵为

(14)

将式(14)与vn相乘，即可分离出第n个距离模糊分量为

(15)

完成所有方位子波束信号的距离解模糊后，对每个距离测绘带对应的信号，补偿不同方位子波束分时发射产生的距离时延，然后进行方位频带拼接，从而获得完整的方位频谱．最后，再对各距离测绘带进行距离图像的拼接，就可以得到方位和距离都不模糊的信号．此时利用相应的常规单通道SAR成像算法，就可以完成高分辨大测绘带场景的成像．

需要注意的是，距离向DBF为了使其有用信号方向增益最大，同时使零点指向邻近子脉冲回波方向，需要距离向DBF形成的窄波束宽度小于相邻子脉冲之间回波方向的夹角．由此可得天线距离向尺寸Dr需满足的条件[13]为

Dr≥2λRfartanθmax/(cΔTmin) ，

(16)

其中，Rfar为场景最远端斜距；θmax为最大下视角，即场景最远端对应的下视角；ΔTmin是属于同一方位子波束信号的不同距离测绘带回波间的最小时延．另外，这里的距离DBF解模糊方法假设地面平坦，实际上地形高度起伏也会影响距离DBF的性能，文献[10]对此进行了详细分析，这里不再赘述．

5 仿真分析

为了验证文中提出的二维脉内扫描面阵SAR模式以及解模糊算法的有效性，利用表1中的系统参数进行仿真分析．设面阵天线距离总高度为 0.26 m，天线方位总长度为 14.8 m，将面阵天线均匀分割为 2×3 的子孔径，即俯仰维划分为2个子孔径，每个子孔径含10个阵元，阵元间距为 0.13 m，方位维划分为3个子孔径，每个子孔径含380个阵元．将脉冲宽度Tp等分为6个子脉冲，每个子脉冲时宽Tpi=Tp/6．

表1 仿真系统参数

仿真中将二维脉内扫描面阵SAR的观测场景分为远近两个俯仰测绘带，每个俯仰测绘带由前、中、后3个方位子波束分时进行扫描，各得到3个方位子测绘带，如图1所示．远测绘带和近测绘带中分别设置了多个点目标，场景如图5所示．

图5 仿真场景与点目标分布

单个子孔径接收到的回波的方位频谱如图6(a)所示，由于远近测绘带中的点目标满足距离模糊等式，两个子测绘带中的场景在距离上模糊在一起，同时由于3个方位子波束分时发射，且PRF小于方位总带宽，属于3个方位子波束的多普勒频带之间在距离上错开，在方位上混叠．因此，图中显示出3块互相交叠的频谱，这时信号存在距离和方位两维模糊．首先利用文中提出的利用方位多通道DBF解方位模糊算法，一一分离出方位子波束信号，得到的子波束信号分别如图6(b)～(d)所示．此时，补偿掉不同方位子波束发射时延，然后进行方位带宽拼接，就可得到完整的方位带宽．

图6 方位解模糊前后的方位频谱

得到信号的完整方位频谱后，回波在距离上还是模糊的，此时直接进行SAR成像得到的结果如图7(a)所示．从图7(a)可知，由于场景中的点满足距离模糊等式，不同俯仰子测绘带的场景的成像结果相互叠加在一起，远近两个俯仰测绘带中的点目标不能区分，需要进一步解距离模糊．利用文中提出的俯仰DBF对距离模糊的信号进行分离之后，可以分别得到远、近两个距离测绘带的完整方位频谱，从而得到理想的二维无模糊的成像结果分别如图7(b)和图7(c)所示．从图7(b)和图7(c)中可知，远测绘带和近测绘带场景均得到了恢复，得到了无模糊的图像．

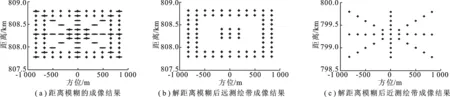
图7 距离解模糊前后的成像结果

6 结 束 语

提出了一个在单脉冲发射时间内进行脉内俯仰-方位二维扫描以实现高信噪比高分辨大测绘带的SAR成像模式．该成像模式无论在信号发射还是接收时都充分利用了面阵资源和二维自由度，提高了天线发射通道利用率，提高了回波的信噪比，同时具有俯仰维和方位维脉内扫描系统的优点，并解决了此SAR成像模式下，回波数据存在的较为复杂的方位模糊和两种距离模糊的新问题，有效解决了二维模糊，实现了高信噪比高分辨大测绘带成像．

[1] Xu Wei. Deng Yunkai, Wang R. Multichannel Synthetic Aperture Radar Systems with a Planar Antenna for Future Spaceborne Microwave Remote Sensing [J]. IEEE Aerospace & Electronic Systems Magazine, 2012, 27(12) : 26-30.

[2] Kim J H, Younis M, Prats I P, et al. First Spaceborne Demonstration of Digital Beamforming for Azimuth Ambiguity Suppression [J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1) : 579-590.

[3] Callaghan G D, Longstaff I D. Wide-swath Space-borne SAR and Range Ambiguity [C] // Proceedings of the International Radar Conference. Stevenage: IEE, 1997 : 248-252.

[4] Krieger G, Gebert N, Moreira A. Unambiguous SAR Signal Reconstruction from Nonuniform Displaced Phase Center Sampling [J]. Geoscience and Remote Sensing Letters, 2004, 1(4) : 260-264.

[5] Federica B, Marwan Y, Gerhard K. Ambiguity Suppression by Azimuth Phase Coding in Multichannel SAR Systems [J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2) : 617-629.

[6] Sun Guangcai, Xing Mengdao, Xia Xianggen, et al. Multichannel Full-Aperture Azimuth Processing for Beam Steering SAR [J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(9) : 4761-4778.

[7] Younis M, Fischer C, Wiesbeck W. Digital Beamforming in SAR Systems [J] . IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(7) : 1735-1739.

[8] Suess M, Grafmueller B, Zahn R. A Novel High Resolution Wide Swath SAR System [C] // IEEE Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2001 : 1013-1015.

[9] Krieger G, Gebert N, Moreira A. Multidimensional Waveform Encoding: A New Digital Beamforming Technique for Synthetic Aperture Radar Remote Sensing [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 31-46.

[10] 武其松, 邢孟道, 刘保昌, 等. 脉内聚束SAR方位高分辨率宽测绘带成像 [J]. 西安电子科技大学学报, 2010, 37(4) : 677-682.

Wu Qisong, Xing Mengdao, Liu Baochang, et al. High Azimuth Resolution Wide Swath Imaging Based on the Intrapulse Spotlight SAR [J]. Journal of Xidian University, 2010, 37(4) : 677-682.

[11] 武其松, 邢孟道, 刘保昌, 等. 面阵MIMO-SAR大测绘带成像 [J]. 电子学报, 2010, 38(4) : 817-824.

Wu Qisong, Xing Mengdao, Liu Baochang, et al. Wide Swath Imaging with the Plane-Array MIMO-SAR System [J]. Acta Electronica Sinica, 2010, 38(4) : 817-824.

[12] 武其松, 井伟, 邢孟道, 等. 多维波形编码信号大测绘带成像 [J]. 西安电子科技大学学报, 2009, 36(5) : 801-806.

Wu Qisong, Jing Wei, Xing Mengdao, et al. Wide Swath Imaging with Multidimensional Waveform Encoding [J]. Journal of Xidian University, 2009, 36(5) : 801-806.

[13] 齐维孔, 禹卫东, 祁海明. 星载MIMO-SAR与距离向DBF相结合系统研究[J]. 电子学报, 2010, 38(10): 2251-2257.

Qi Weikong, Yu Weidong, Qi Haiming. Study of the System Combining Spaceborne MIMO-SAR and Elevation DBF [J]. Acta Electronica Sinica, 2010, 38(10) : 2251-2257.