上证基金指数波动结构分解与短期预测:基于EEMD模型
何 凯,苏梽芳,2,何卫平
(1.华侨大学 经济与金融学院,福建 泉州 362021;2.中国社会科学院经济研究所 博士后流动站,北京 100000;3.暨南大学 经济学院,广东 广州 510000)
上证基金指数波动结构分解与短期预测:基于EEMD模型
何 凯1,苏梽芳1,2,何卫平3
(1.华侨大学 经济与金融学院,福建 泉州 362021;2.中国社会科学院经济研究所 博士后流动站,北京 100000;3.暨南大学 经济学院,广东 广州 510000)
上证基金指数反映了基金市场的整体变动情况,研究其波动结构特征对基金市场参与者具有重要作用。研究结果表明:(1)上证基金指数序列可由经济基本面决定的趋势项、重大事件带来的低频分量和短期不均衡导致的高频分量构成,而且趋势项主导上证基金指数的长期走势,低频分量在中期对该指数有较大影响,而高频分量的影响可忽略不计;(2)与直接SVM预测法相比,EEMD-SVM组合预测法有更高的预测精度,说明EEMD分解得到的各结构分量有效地刻画了上证基金指数的内在运行特征。
证券市场;集成经验模态分解;本征模态函数;支持向量机;上证基金指数
一、引言
证券投资基金作为我国最大的机构投资者,其在我国资本市场中的地位日渐凸显。从它出现至今一直受到机构和个人投资者的青睐和社会各界的广泛关注。证券投资基金不仅可以有效地改善证券市场的投资结构,而且其作为一种新型的金融工具,还拓宽了人们的投资渠道和改善了金融市场的运行。近年来,对证券投资基金的研究文献逐渐增加,主要集中于基金业绩评价、封闭式基金折价现象的分析、机构投资者持股对股市是否具有稳定作用以及基金内部治理结构等方面。然而,对于基金指数的波动性研究及基金净值预测的方法,研究角度还比较单一,而且没有深入挖掘基金运行的内在结构特征。而这恰恰对于投资者、监管者以及基金管理者更好地认识和了解我国封闭式基金市场近年来的运行情况、风险特征与市场趋势具有重要作用。
一方面,对于基金指数的波动性研究,目前主要是运用数据驱动的方法,如ARCH类、GARCH模型和ARMA模型等。郭晓亭(2006)[1]分别运用EGARCH和TGARCH模型对中信基金指数波动的非对称性和杠杆效应进行了实证研究;牛方磊和卢小广(2005)[2]运用ARCH模型族进行实证分析,得出上证基金指数收益率表现出非正态性和条件异方差的特征;杨湘豫和周屏(2006)[3]认为华安创新基金收益率存在异方差性和不对称的现象,并且EGARCH (2,2)模型能较好模拟该基金收益率的特征。虽然此类数据驱动的方法在短期上有好的研究效果,但是却不能有效地解释证券投资基金的经济含义和其波动的内在驱动力。而Huang etal.(1998)[4]提出的经验模态分解法(Empiricalmode decomposition,EMD)能有效地解决这个困境。该法能很好地处理非平稳、非线性信号,被认为是对以线性和平稳假设为基础的傅立叶分解和小波基的重大突破,具有直观、直接、后验和自适应的优点,其根本原因在于这种变换是基于数据本身的一种分解,而不是基于事先设定好的基函数。近年来,该法也开始应用于经济金融领域,如Zhang et al.(2008)[5]、王晓芳和王瑞君(2012)[6]。但EMD分解的一个重要缺陷是模态混叠,为克服该缺陷,Wu和Huang(2009)[7]提出具有有效的抗混分解能力的集成经验模态分解(Ensemble EMD,EEMD)方法。另一方面,对于基金净值和基金指数的预测主要有两类:一是统计方法,如基于AR、MA、ARMA和GARCH等模型的预测,这类方法是一种参数方法,首先要定义模型的具体形式,再根据历史数据找出最优参数,但这容易导致模型不匹配;二是人工智能法,主要是人工神经网络方法,该法是一种数据驱动的非参数法,容易避免模型不匹配问题,并有较强的泛化能力和噪声容忍能力等优点,如肖国荣(2011)[8]用BP神经网络预测了金泰基金价格,刘丽峰(2011)[9]提出采用粒子群优化与BP神经网络相结合的组合模型,用于基金净值预测研究。但神经网络存在过度学习与维度灾难的缺陷。而支持向量机(Supportvectormachine,SVM)却可以有效地避免该问题,如傅东升和曹丽娟(2007)[10],Xieetal.(2006)[11]。然而,目前对于基金指数的预测大多都是针对序列本身,而没有充分的考虑其内在的运行特征。
因此,本文基于集成经验模态分解方法,将上证基金指数分解为若干不同频率的分量以探究其波动的结构性特征,为认识上证基金指数的波动提供新思路。为提高基金指数预测精度,本文提出了基于EEMD分解得到的各个本征模态函数,根据其各自不同的特征,建立相应的SVM回归预测模型进行预测,再将各本征模态函数的预测值等权重叠加得到最终的预测值,并用MAPE、RMSE和DS等指标对该模型的预测效果进行评价。
二、经验模态分解方法
(一)经验模态分解(EMD)理论与算法
Huang etal.(1998)提出了经验模态分解方法(EMD),该分解方法具有直观、直接、后验和自适应的优点。该法是基于时间序列内在的特征,自适应地通过筛选过程(Sifting process)从序列中提取出独立的、不同频率的本征模态函数(Intrinsic mode function,IMF),每个IMF可以是线性的,也可以是非线性的,它反映了上证基金指数内在的波动特性。EMD方法假设任何信号都是由一系列包含了原信号的不同时间尺度的局部特征信号的本征模态函数(IMF)组成,这种IMF分量必须满足两个条件:即其极值点个数和过零点数相同或最多相差一个以及其上下包络关于时间轴局部对称。从而EMD方法就可以将一个多分量信号的各阶本征模态分量一一筛选出来,具体步骤如下:设时间序列为x(t)。
(1)首先计算x(t)所有的局部极大值点和局部极小值点;
(2)用三次样条插值分别连接所有局部极大值和局部极小值点,构造x(t)的上包络线xmax与下包络线xmin;
(3)根据求得的上下包络线,计算均值包络线,记为m1(t),以及x(t)与m1(t)的差值,记为h1(t),即:m1(t)=(xmax+xmin)/2,h1(t)=x(t)-m1(t);
(4)因为h1(t)一般不是一个IMF分量,为此需要对它重复上述处理过程k次,直到h1k(t)=h1(k-1)(t)-m1k(t)符合IMF的定义要求,即认为h1k(t)是一个IMF分量,记c1(t)=h1k(t),r1(t)=x(t)-c1(t),x(t)=r1(t);
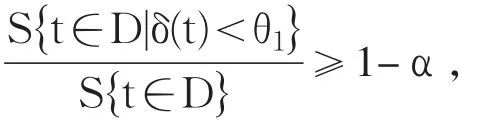
(二)集成经验模态分解(EEMD)
为克服EMD分解出现的模态混叠现象,Wu和Huang(2009)提出了Ensemble EMD方法(EEMD)。EEMD的基本思想是每一个观察数据都是白噪声与真实数据的融合,即使每个数据的搜集是单独观察到的,并且每次观测的白噪声都不同,但最后通过集成平均可消除白噪声的影响,可得到真实的序列。EEMD的分解步骤如下:第一,对目标序列增加一列白噪声;第二,在对增加白噪声后的序列进行分解;第三,重复上述步骤,但每次增加的白噪声不一样,把得到IMF的集成均值作为最后的结果。
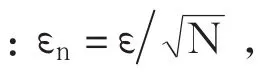
三、证券投资基金波动的结构性特征实证分析
(一)数据说明与统计描述
本文选取上证基金指数收盘价为研究对象,样本范围选取2000年5月10日至2013年4月3日的日数据,数据来源于国泰安数据库(CSMAR)。本文用matlab7.0来处理数据。样本数据的时间序列,如图1所示。
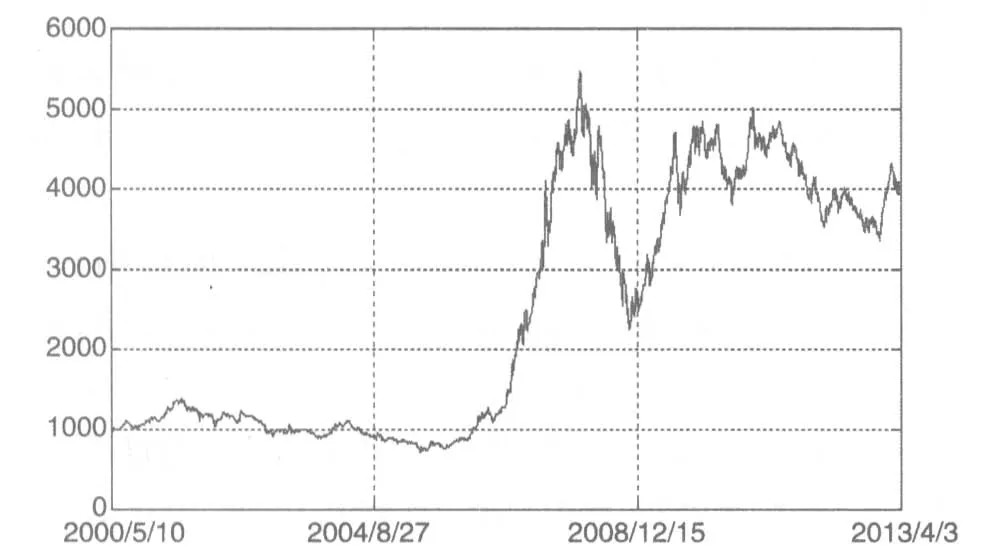
图1 上证基金指数

表1 上证基金指数统计分析
从表1可知,上证基金指数的偏度为0.293,峰度为1.34,说明上证基金指数序列为一个为右偏的宽尾分布。
(二)EEMD分解以及各IMF的统计分析
在EEMD模型中,设定加入的白噪声的标准差为0.2,集成次数为100。根据Rilling,etal.(2003)提出的终止条件,上证基金指数经分解得到8个IMF和一个余项(图2)。分解出来的所有IMF都是按频率从高到低排列,且各IMF呈现出相似的波动特征,即随本征模态函数从高频到低频移动而振幅增加;而余项即趋势项是一个单调递增的缓慢变化的时间序列。
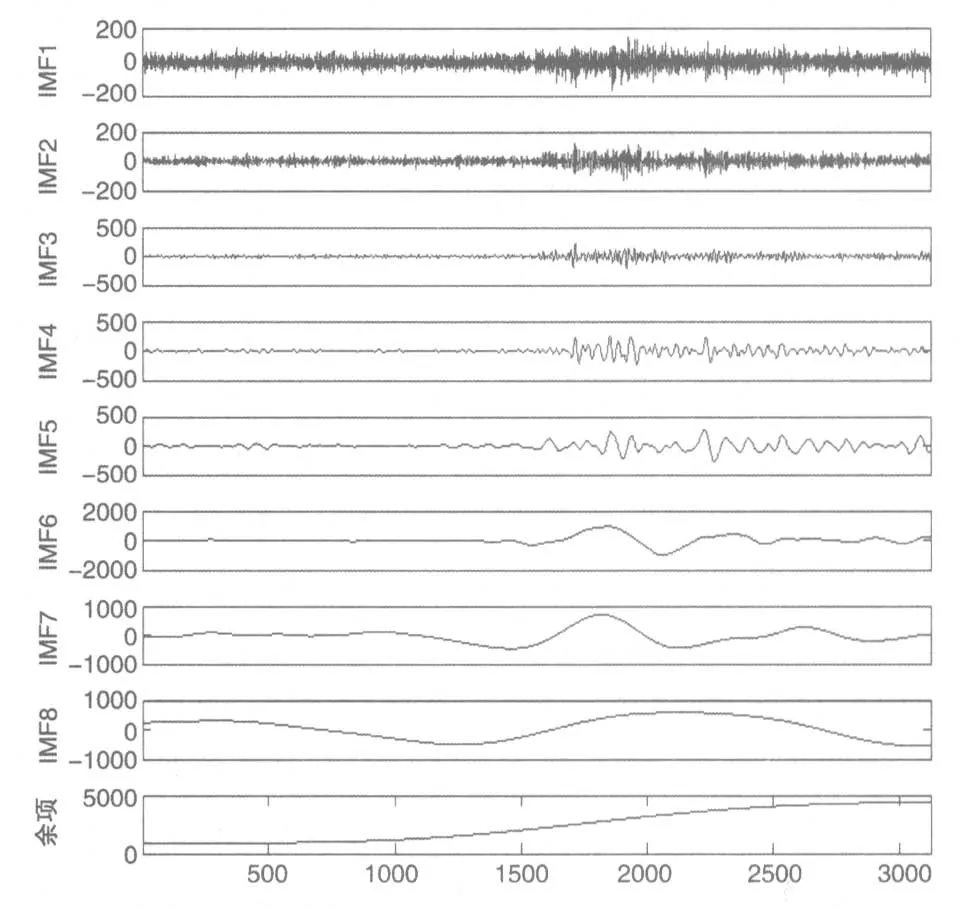
图2 上证基金指数的本征模态函数和趋势项
下面我们主要从Pearson系数大小、平均周期、占上证基金指数的方差比和占分解后各IMF和趋势项方差之和的比值这四个指标来分析各IMF、余项与原始序列的关系。Pearson相关系数用来衡量每个IMF以及余项与原始序列的相关性大小。每个IMF的平均周期等于该IMF的样本数与其所有极大值点个数的比值与所有极小值点个数的比值的平均值,用平均周期来反映每个IMF的频率变化主要是因为IMF的频率和振幅随着时间的推移发生细微变化,致使IMF的周期不是一个恒定值。另外,由于这些IMF彼此间相互独立,因此可用每个IMF的方差分别占原始序列方差的比例和占分解后各IMF和趋势项方差之和的比值来解释其对原始序列波动的贡献率。
由表2可知,各IMF的平均周期和相关系数从上到下逐渐变大。IMF1的平均周期为2.86天,Pearson系数为0.014。而IMF8的平均周期最长,即1302.9天,Pearson系数为0.36。这表明高频IMF与原始序列的相关系数较小可能是由于其周期较短、波动频繁导致;而低频IMF与原序列相关系数较小,其原因可能是低频模式函数周期比较长,趋势方向变化较缓,即当原始时间序列处于某一运行趋势时,这些IMF难以及时调整其运行方向。而IMF至IMF5的方差占原序列方差比之和与占分解后方差比之和分别都没有超过1%,低频模态函数(IMF6、IMF7和IMF8)和趋势项的方差总和占到总方差的绝大部分。不难发现高频分量对上证基金指数影响不大;在某一段时期内,由政治动乱、金融危机和宏观政策变化等重大事件影响造成的低频分量在某一段时期对上证基金指数影响可能比较大;而在长期内,作为上证基金指数内在运行轨迹的趋势项对其影响最大,这意味着一般情况下大部分本征模态函数对基金市场指数影响都较小。
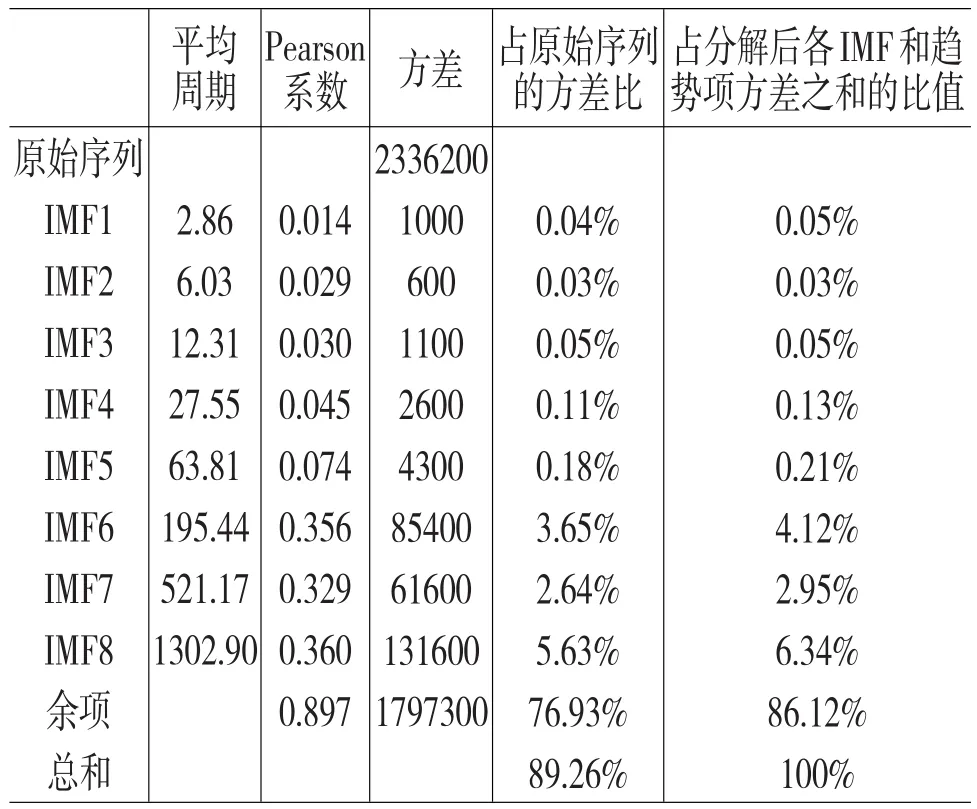
表2 基于EEMD分解的上证基金指数各IMF和余项分析
另外,趋势项轨迹与原始时间序列的运行轨迹基本吻合,而且趋势项和原始序列的相关系数最高,达到0.897,趋势项的方差占分解后各IMF和趋势项方差之和的86.12%,占到原序列方差的76.93%,说明趋势项能解释上证基金指数的波动的绝大部分,正如Huang etal.(1998)中提到,趋势项常被人们视为原始时间序列中的内在运行轨迹。
(三)上证基金指数波动结构特征分析
上证基金指数序列经EEMD分解成8个IMF和一个余项。IMF的频率各不相同,高频分量表现出随机无序性,而低频项具有很强的周期性。我们采用从高频到低频的重构算法(Fine-to-coarse Reconstruction)对各模态本征函数重构,得到上证基金指数的结构分量。重构算法步骤如下:首先,对各模态,计算从IMF1—IMF(i)的和的均值,其中i=1,2,…,8;其次,基于t检验,检验从哪一个i起,对应的均值显著偏离于零,一旦i被识别为结构转折点,则从IMF1—IMF(i-1)的重构被识别为高频分量,而其他IMF的重构被识别为低频分量。
从图3中可以看出,对各IMF的均值进行t检验,发现在IMF6处显著地偏离了零。另外,IMF1-IMF5的均值近似等于零,即基本围绕零均值线随机波动,但从IMF6开始呈现出比较规则的周期性波动。因此,将IMF1-IMF5归为高频分量,而IMF6-IMF8归为低频分量。
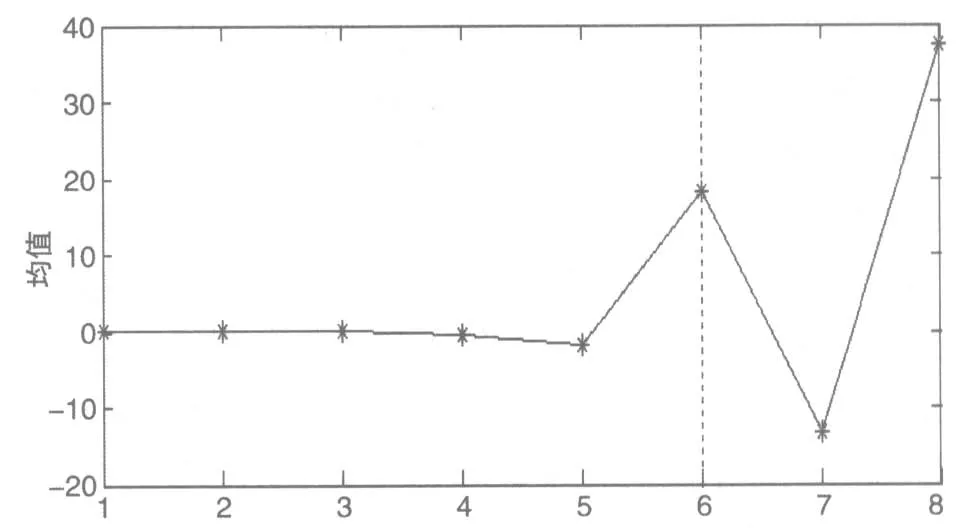
图3 高低频区分判别图
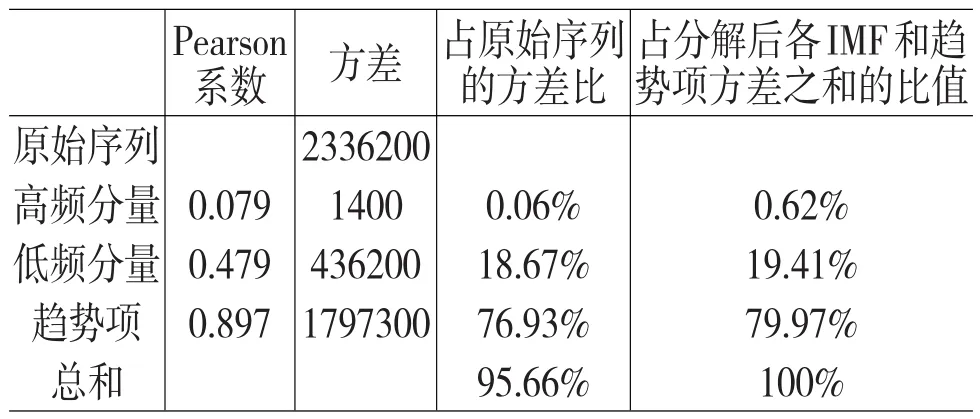
表3 上证基金指数与三部分结构分量的相关系数及方差来源分析
我们发现高低频分量和趋势项隐含着很强的经济学意义,趋势项围绕着长期均值缓慢变化,描述了上证基金指数的长期走势;低频分量的每次波动总是和一些政治动乱、宏观经济政策变化和金融危机等重大事件相关,这都反映出这些重大事件对上证基金指数基金市场的影响;高频分量振幅小、频率高,围绕零均值随机波动,可以用来揭示基金市场短期的不均衡现象,并用其振幅的大小来表征短期不均衡的程度。由于上证基金指数针对的是沪深交易的封闭式基金,反映了基金市场的综合变动情况,故高低频分量与趋势项这三个结构分量可用来揭示隐含在上证基金指数序列和其反映的基金市场的内在运行特征。
从高频分量来看,它代表了基金市场的随机波动,表现了基金市场的短期不均衡程度。由于高频分量中的各本征模态函数周期短、变化快,所以了解基金市场中高频分量的波动特征对短期投资具有一定的意义。由表3可知高频分量和原始序列相关系数为0.079,高频分量占原始序列方差的比例为0.06%,且占分解后各IMF和趋势项之和的方差比也才0.62%,说明短期不均衡造成的随机波动对基金市场的影响有限,市场投机行为不明显,而且高频分量的波动主要是供需不均衡导致,属正常的市场反应,这与我国基金市场特征是相符的。
从低频分量来看,低频分量反映了我国基金市场的中期波动。用低频曲线来表征重大事件对上证基金指数的影响,其中周期表示对指数产生影响的时间长短,振幅表示对指数冲击的大小。换句话说,周期越长,基金市场受重大事件冲击影响的时间就越长;振幅越大,基金市场受事件冲击就越大。重大事件对基金市场产生的冲击主要体现在低频分量(IMF6、IMF7和IMF8)中,这些冲击引起的指数波动幅度大,持续周期长。从图4和表3中观察到,平均周期至少在半年以上,说明上证基金指数需要在相当长的时间才能消化重大事件带来的冲击。具体来说,在重大事件的影响期内,比如2008年的全球金融危机,趋势项变化比较缓慢,而高频分量振幅又小,所以,低频分量是引起上证基金指数大幅波动最主要的原因,且基金市场短期内无法消除这些影响。
从趋势项来看,在表3中,趋势项和原始序列相关系数为0.897,趋势项占原始序列方差的比例将近76.93%,占分解后各IMF和趋势项方差之和的比值为79.97%,说明趋势项基本决定了上证基金指数的长期走势。从图4可见,基金市场总的趋势是上行的,这与我国经济发展情况是一致,因此在长期我国基金市场的运行由我国的经济基本面决定。而且,尽管基金市场常受到一些重大事件的冲击大幅波动,但是待该事件影响结束后,指数仍会返回到趋势附近围绕其小幅波动运行。
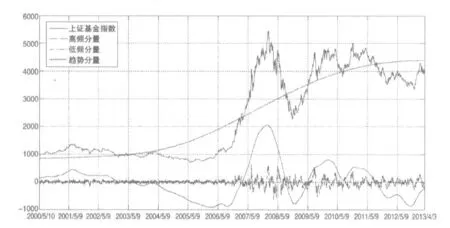
图4 上证基金指数高低频分量和趋势项分解图
四、上证基金指数短期预测
上证基金指数序列是典型的非平稳、非线性时间序列,传统的预测方法基本都是针对整个时间序列进行预测,而没有充分考虑到该序列的随机性、周期性和趋势性的特点,而这样预测的精度还有提高的空间。因此,本文首先采用EEMD分解方法,把上证基金指数序列分解为具有不同频带的分量,对各分量建立相应的支持向量机(Support vectormachine,SVM)回归预测模型进行预测,然后将各个预测结果等权重叠加作为上证基金指数的预测值(即EEMD-SVM组合预测法)。同时,为了检验本文方法的预测效果,将该方法与将上证基金指数序列直接用SVM回归预测方法(即直接SVM法)预测的效果进行比较。本文选用平均绝对百分比误差(MAPE)和均方根误差(RMSE)来度量预测误差的大小;用方向对称值(DS)来度量各模型对上证基金指数方向性走势的预测能力,显示能正确预测目标值方向的次数与预测样本容量的百分比。
Vapnik etal.(1995)[12]在统计学习的理论基础上首次提出支持向量机算法,该算法是一种全新的机器学习算法。SVM的主要思想可以概括为两点:一是可以将低维非线性问题转化为高维的线性问题,用一个核函数代替高维中的内积运算,有效克服维度灾难及局部极小值问题;二是基于结构风险最小原理在特征空间中建构最优分割超平面,使学习器得到全局最优化,故具有良好的泛化能力。由于SVM出色的性能,因而在预测方面得到广泛的运用。
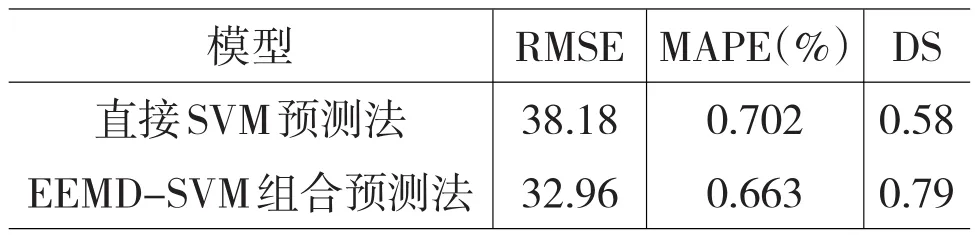
表4 预测误差比较
SVM回归预测的基本思路是对于给定样本数据{xk,yk} ,其中xk∈R为n维向量,yk∈R为相对应的输出变量,寻找一个函数f(x)来推断任意的x所对应的y值。SVM回归预测的具体步骤为:(1)将上证基金指数日收盘价序列从2000年5月10日至2013年5月10日共3147个样本数据分为两部分,其中把2000年5月10日至2013年4月3日共3127个样本数据作为训练数据,将2013年4月8日至2013年5月8日共20个交易日的数据作为测试数据,同时将上证基金指数日收盘价序列进行EEMD分解,得到8个不同频带的IMF及余项;(2)本文利用所研究时间序列的过去10天的历史值来预测未来一天的值,对各IMF及余项先处理得到各自的训练样本和训练目标,其中训练样本为一个10行3117列的矩阵,训练目标为一个1行3117列的向量,为提高收敛速度将这两类训练样本归一化为0~1之间;(3)选用径向基函数为核函数,利用交叉验证与网格搜索法选择误差值最小时的惩罚参数与核参数,建立相应的SVM回归预测模型;(4)采用移动窗口的一步向前预测法,利用相应的SVM回归预测模型预测得到不同频带未来20天的预测值,将各频带的预测值等权重叠加得到最终的预测值。本文基于Matlab7.0平台的Libsvm2.89软件包(http://www.csie.ntu.edu.tw/~cjlin/)进行预测。具体预测结果与预测误差比较如表4与图5:
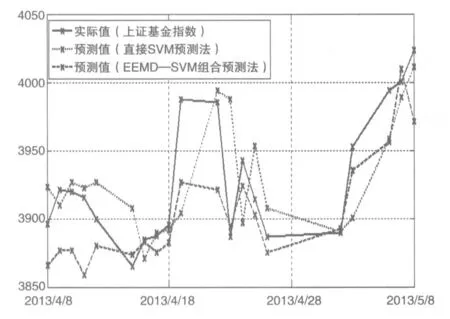
图5 预测值与实际值比较
从表4可以看出,EEMD-SVM组合预测法的RMSE和MAPE分别为32.96与0.663%,直接SVM预测法的RMSE和MAPE分别为38.18与0.702%,而且从图5可知,对于从2013年4月8日至2013年5月8日共20个交易日的预测数据,在绝大部分时点上,EEMD-SVM组合法的预测值较直接SVM法的预测值更接近于真实值,这说明EEMD-SVM组合预测法较直接SVM预测法的相对误差小,预测精度高;另外,EEMD-SVM组合预测法的DS为0.79,大于直接SVM法的0.58,说明前者更好地把握了上证基金指数的走势方向。因此,本文提出的EEMD-SVM组合预测法较直接SVM预测法有更高的预测能力。
五、结论
本文首先利用EEMD分解方法,将上证基金指数分解为8个IMF和一个趋势项,进一步将其重组为高频分量、低频分量和趋势项三个结构分量。其中,高频分量代表了上证基金指数波动的随机性特征,反映了市场的短期不均衡,而且其平均周期较短,方差占上证基金指数波动的比重较小,说明基金市场投机行为较少;低频分量代表了上证基金指数波动的周期性特征,反映了重大事件对市场上证基金指数中期波动的影响,其平均周期较长,方差占上证基金指数波动的比重较大,说明基金市场受重大事件的影响较大;而趋势项主导上证基金指数的长期走势,反映了经济基本面的影响,并且其方差能解释上证基金指数波动的绝大部分。
其次,利用经EEMD分解得到的不同本征模态函数,建立相应的SVM回归预测模型进行预测,最后将各分量的SVM预测值等权重加总得到最终的预测值。预测结果显示,EEMD-SVM组合预测法的预测效果要优于直接SVM预测法,这说明了EEMD分解充分考虑了上证基金指数的周期性、随机性和趋势特性,从而提高了预测精度。
必须指出的是,由于上证基金指数序列是一个复杂的系统,受到国内外众多因素的影响,仅从该时间序列自身出发,建立相关模型进行预测,预测精度可能还有提高的空间。因此,把影响上证基金指数的主要变量纳入到预测模型中,建立SVM时间序列预测模型进行预测是一个研究方向。
[1]郭晓亭.中国证券投资基金市场波动特征实证研究[J].中国管理科学,2006,14(1):15-20.
[2]牛方磊,卢小广.基于ARCH类模型的基金市场波动性研究[J].统计与决策,2005,(12X):109-110.
[3]杨湘豫,周屏.GARCH模型在开放式基金中的实证研究[J].系统工程,2006,24(4):73-76.
[4]Huang,Norden E,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences 454.1971 (1998):903-995.
[5]Zhang X,LaiK K,Wang SY.A New Approach for Crude Oil Price Analysis based on Empirical Mode Decomposition[J].Energy Economics,2008,30:905-918.
[6]王晓芳,王瑞君.上证综指波动特征及收益率影响因素研究——基于EEMD和VAR模型分析[J].南开经济研究,2012,(006):82-99.
[7]Wu Z H,Huang N E.Ensemble Empirical Mode Decomposition:A Noise-assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009, 1(1):1-41.
[8]肖国荣.BP神经网络在基金价格预测中的应用研究[J].计算机仿真,2011,28(3):373-376.
[9]刘丽峰.组合模型的基金净值预测研究[J].计算机仿真,2011,28(5):354-357.
[10]傅东升,曹丽娟.SVM与BP网络对基金波动的预测效果比较分析[J].世界经济情况,2007,(8):45.
[11]Xie W,Yu L,Xu S,et al.A New Method for Crude Oil Price Forecasting based on Support Vector Machines[M].Computational Science-ICCS 2006. Springer Berlin Heidelberg,2006:444-451.
[12]Cortes C,Vapnik V.Support-vector Networks [J].Machine Learning,1995,20(3):273-297.
(责任编辑:贾伟)
ract:Shanghai Securities Fund Index reflects the overall changes in fund market,so investigating its volatility structure is of the utmost importance to investors in thismarket.The results show that ShanghaiSecurities Fund Index can be composed of the trend series dominated by economic fundamentals,high frequency series created by short-term disequilibrium and low frequency series caused by big events;moreover,the trend decides the long-term trend of Shanghai Securities Fund Index,low frequency atmedian term exerts large influence upon it,buthigh frequency has little impacton it.Additionally,the forecasting results demonstrate effectiveness and attractiveness of the proposed EEMD-based SVM ensemble learning paradigm compared with single SVM,which illustrates that the EEMD decompositionmethod effectively depicts the inherent characteristics of Shanghai Securities Fund Index.
ords:stock market;ensemble empiricalmode decomposition(EEMD);intrinsicmode function (IMF);supportvectormachine(SVM);Shanghaisecurities fund index
1003-4625(2014)01-0080-06
F830.91
A
2013-10-20
本文为国家社会科学基金(11CJY104);福建省高等学校新世纪优秀人才支持计划(2012FJ-NCET-SK02);福建省高等学校杰出青年科研人才培育计划(11FJPY04)。
何凯(1988-),男,湖南沅江人,信息经济学硕士研究生,研究方向:金融市场与货币经济学;苏梽芳(1977-),男,福建惠安人,华侨大学经济与金融学院副教授,金融系主任,中国社会科学院经济所理论经济博士后,研究方向:金融计量与通货膨胀;何卫平(1988-),男,湖南邵阳人,数量经济学硕士研究生,研究方向:金融计量学。

