考虑时间均衡度的城市轨道交通乘务排班计划优化方法

丰 富，陈绍宽，杜 鹏

（北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京100044）

考虑时间均衡度的城市轨道交通乘务排班计划优化方法

丰 富，陈绍宽*，杜 鹏

（北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京100044）

乘务排班计划是城市轨道交通乘务组织的核心内容和运营管理工作的重要组成部分，其生成质量对城市轨道交通的运营效率有显著影响.本文将时间均衡度作为给定周期条件下评价乘务员值乘时间与休息时间合理程度的指标，构建了基于该均衡度的乘务排班计划优化模型.为同时考虑乘务区段的最优组合与早晚班的匹配问题，本文的求解过程由改进遗传算法和双相匹配算法两个部分构成.最后将所建模型应用于北京市某轨道交通线路的案例研究中，对优化结果与既有乘务计划进行比较分析，验证模型的有效性.对比发现，该模型的结果在较大程度上提高了乘务排班计划的时间均衡度.

城市交通;城市轨道交通；优化模型；遗传算法；乘务排班计划；时间均衡度

1 引 言

乘务排班计划是交通运输运营组织工作中的重要环节之一，其实质是在给定运行时刻表及运输工具的接续关系后，制定乘务人员的工作计划.如果将乘务人员的工作时间作为生产投入，则乘务计划可转化为一个资源配置问题，合理的乘务计划可为运输企业带来可观的经济效益[1].

近年来有关乘务计划问题的建模和求解算法方面的研究得到广泛开展.建模方面的主要研究工作主要分为三类：集划分或集覆盖形式的模型、以值乘区段或值乘交路间的接续关系为决策变量的物理模型，以及以图的结构或者其他方式描述乘务问题的模型[2-4].例如，张增勇等建立了考虑乘务作业段和工作班生成的基于惩罚费用的双层模型，并设计了Dijkstra算法和离散粒子群算法进行求解[5].李献忠与徐瑞华合作，从时间耗费和广义费用两个角度进行了乘务优化研究，获得的排班计划显著提高了乘务工作的质量和效率，相对于传统依赖经验的人工编制乘务计划表现出明显的优势[6,7].Zaepfel和Boegl在考虑值乘区段或值乘交路间的接续关系时加入与乘务员相关的因素，对乘务员的休息时间的安排进行了研究[8].

实际排班工作中，对乘务员的值乘时间、休息时间，以及两者均衡程度方面关注更多，但目前尚无较深入的研究成果.列车运行图规模较大时，由于工作环境和值乘需求，乘务员的工作量和休息时间的分配可能会出现较严重的局域倾斜现象[8].在实际的运营管理中，乘务员的人数与运营中的需求之间应基本平衡且留有余量.然而就乘务员个体来说，乘务任务和休息时间往往很难实现理想的平衡[9].

本文考虑合理分配乘务员值乘和休息时间因素，提出基于时间均衡度的优化目标函数，构建乘务排班计划模型，并设计适当的求解算法搜寻满意解，为乘务排班计划的制定与优化提供方法支撑.

2 问题描述

城市轨道交通排班计划是根据给定的列车运行图、乘务规则、动车或车底交路、乘务基地条件等，考虑一定的优化目标，对乘务员的出退乘时间与地点、值乘车次与时刻等做出具体安排，以确保列车运行计划的实现[10].编制排班计划的一般流程是：分割列车运行径路形成值乘区段；根据乘务规则和优化目标将值乘区段进行组合；如果考虑较长时间的排班计划，可进一步编制长周期乘务排班计划.

乘务排班计划编制过程中一般根据乘务基地对于资源配置和停留时间的要求，选择较大型且停留时间较长的可换乘车站作为乘务基地[11].在确定乘务基地的基础上，以其为节点对列车运行线进行分割，进而形成列车乘务员的值乘区段.乘务排班计划工作则是按照乘务规则对值乘区段进行分配，形成值乘交路，同时实现值乘时间、乘务员数量等评价指标的最优化[12].

在乘务规则方面主要有以下考虑.

（1）值乘区段的完全覆盖.每一个值乘区段都有其对应的值乘交路，值乘交路与值乘区段的归属关系方面遵从互斥原则.

（2）值乘区段的邻接关系.值乘区段序列中前后两个相邻的值乘区段必须满足一定的时间间隔.

（3）值乘时间约束.指乘务员的值乘时间具有规定的上下限.

（4）休息时间限制.指乘务员连续值乘时间达到某一阀值的时候必须安排休息时间.休息时间通常分为两种，相邻值乘区间之间的休息时间和晚班与早班之间的夜间休息时间.在城市轨道交通运营工作中，通常是指晚班值乘的乘务员继续值乘接续早班的夜间休息时间.

（5）吃饭时间约束.乘务员值乘期间的吃饭时间必须按规定进行设置.

3 模型构建

3.1 时间均衡度

时间均衡度是由排班计划的时间成本、乘务员值乘时间和夜间休息时间共同衡量，旨在兼顾排班计划的时间成本与乘务员工作时间、休息时间分配的合理程度.乘务排班计划优化模型的目标函数如下所述.

（1）乘务排班计划值乘时间成本.

乘务排班计划的时间成本是由值乘交路的值乘时间和时间价值共同确定的.具体的计算公式为

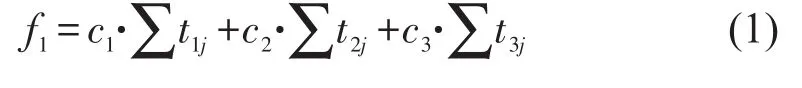
式中 t1j、t2j、t3j是早班、白班、晚班值乘交路 j的持续时间（小时）；c1、c2、c3分别是其对应的时间价值（元/小时）.

（2）值乘时间均衡程度.

值乘时间的均衡程度是指排班计划中同一班次中所有乘务人员的值乘时间的均衡程度，本文采用隶属度函数表示，隶属度越大则值乘时间均衡度越好.值乘时间均衡程度的隶属度函数式为

其中，fun1() t1j是早班值乘时间的隶属度，其解析式为

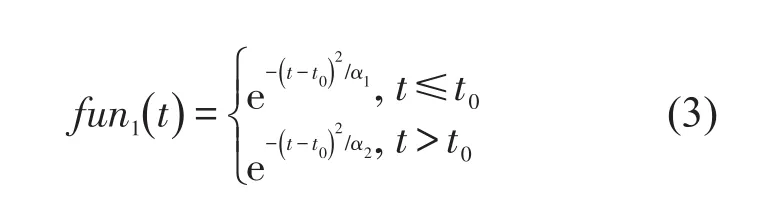
式中 参数t0、α1、α2由早班值乘时间的数据样本来确定.类似地，可确定 fun2(t2j)和 fun3(t3j).

（3）夜班时间均衡程度.

夜班时间的均衡程度主要体现为“晚-早同员”乘务员的夜间休息时间和夜班值乘时间的差异程度.夜间休息时间是指乘务员晚班下班至早班上班之间的休息时间，其差异程度越小则均衡度越好.具体的计算公式为

式中 {d ri}是“晚-早同员”乘务员的集合；D(·)是方差函数；β是权重系数；D(tn)是乘务员夜间休息时间的方差；D({ dri})是“晚-早同员”乘务员夜班值乘时间的方差.

（4）时间均衡度.

f1、f3的值增大时，时间均衡度增大；f2增大时，时间均衡度减小.因此定义时间均衡度为

式中 k为权重调整系数.

3.2 优化模型

考虑时间均衡度的乘务排班计划优化模型以时间均衡度为目标函数，以值乘区段的完全覆盖、值乘区段的邻接关系、值乘时间约束、休息时间限制和吃饭时间约束为约束条件.具体的排班计划优化模型如下.

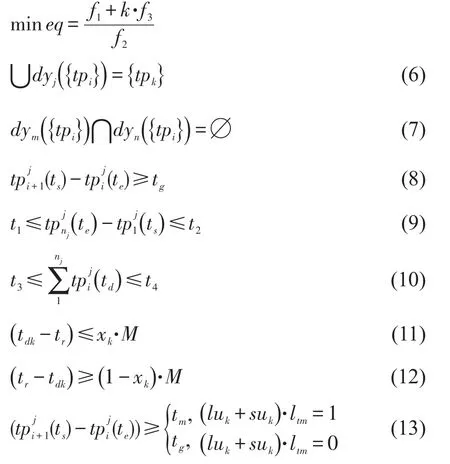
式中 tpi(i ,ts,te,td)——表示值乘区段i的信息，i是值乘区段的编号，ts是该值乘区段的开始时刻，te是该值乘区段的结束时刻，te是该值乘区段的持续时间；

dyj(j ,cj,{t pi})——表示值乘交路 j的信息，j是值乘交路的编号，cj是值乘交路 j对应的乘务员，{tpi}的是组成值乘交路 j的值乘区段的集合，tpi按时序排列；

drk(k ,tdk,luk,suk)——表示乘务员k的信息，其中k是乘务员的编号，同对应的值乘交路的编号相同，tdk是其连续的值乘时间.luk为0-1变量，取1时该乘务员需要午餐时间，取0时则不需要，suk为0-1变量，取1时该乘务员需要晚餐时间，取0时则不需要.

式(6)保证值乘交路对值乘区段的完全覆盖.

式(7)描述了值乘区段和值乘交路的唯一对应关系.

式(9)为值乘时间约束.其中,nj是属于值乘交路 j的值乘区段的数目;分别是值乘交路j中最后一个值乘区段的结束时刻、第一个值乘区段的开始时刻，即值乘交路 j的结束时刻和开始时刻.

式(11)、式(12)为夜间休息时间限制.其中，xk是0-1变量，取1表示乘务员k的连续值乘时间已经超过阀值而必须进行休息；M是一个大数.

式(13)为进餐时间约束.其中，tm是进餐间隔，实际中至少为24 min；lm是0-1变量，用来判断当前时刻是否处于进餐区间中：ltm取1时表示当前时刻处于进餐区间中，否则不处于进餐区间中.

4 求解算法

针对上述构建模型的特点，设计求解算法如下.

（1）求解思路.

模型的求解过程分为三步，首先是值乘区段组合构成值乘交路的过程，然后再使用双向匹配来完成“晚—早同员”的搭配，最终计算优化整个排班计划的时间均衡度.

根据乘务规则，对列车运行线进行分割，从而得到值乘区段集合.值乘区段按照乘务规则进行组合，形成值乘交路.值乘交路分成早班、白班和夜班三个班次，使用双向匹配来完成“晚—早同员”的搭配.

（2）遗传算法及流程.

求解上述模型采用遗传算法，染色体采用0-1编码.染色体设置为m×n的矩阵（Am×n），其中m是值乘区段的个数，n是班次的数目（排班计划包含早班、白班和晚班）.该矩阵中的元素xij为0-1决策变量，xij=1时值乘区段i被分配在班次 j中，xij=0则值乘区段i不在班次 j中.根据值乘区段的唯一完全覆盖约束，有

遗传算法的适应度函数由模型的目标函数和惩罚函数两部分组成，其公式为

式中 pi(Am×n)是第i个约束条件对应惩罚函数.

求解算法由初始种群的产生、交叉、变异、适应度函数计算和求解过程终止判断五个环节组成.交叉、变异等操作均通过改变染色体矩阵中某些行的顺序完成，算法流程如图1所示.图1中虚线框内染色体根据乘务规则确定方法分为三个班次，左侧的操作是不同班次的值乘时间和休息时间的隶属度函数的计算，右侧则是使用遗传算法获得最优的“晚—早同员”匹配.这两部分的计算结果与惩罚函数的和作为染色体的适应度函数.

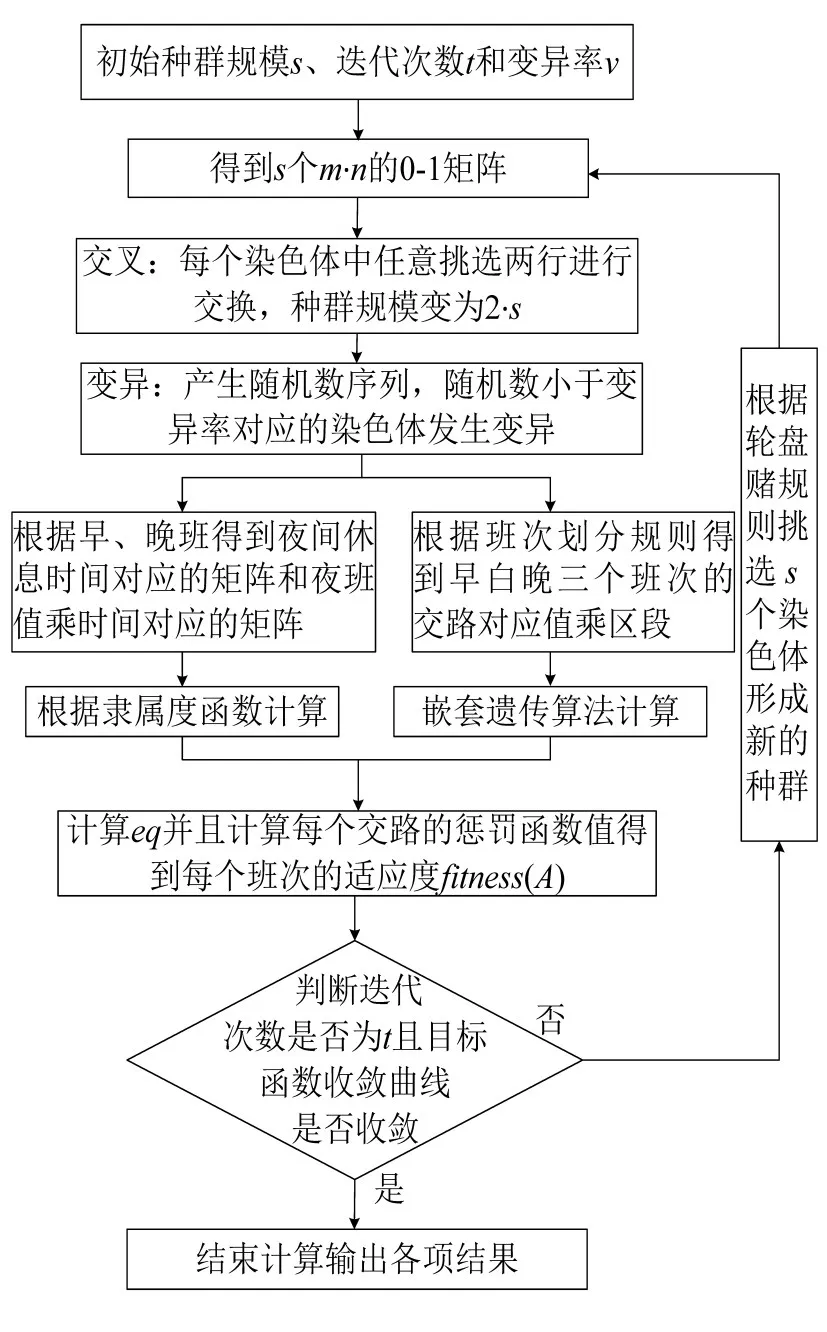
图1 算法流程图Fig 1 Flow chart of the developed algorithm

5 案例研究

本文以北京某城市轨道交通线路作为案例进行所建优化模型的验证分析.该线作为北京城市轨道交通网络东西向骨干线路的东段延长线，连接了北京中心城区及东部的新城.全长19.0 km，共设13座车站，乘务基地设置在最东端的尽头站.客流高峰时最小追踪间隔3.5 min.值乘区段平均时长1 h 6 min.既有排班计划采用人工编制，主要依赖于编制工作人员的经验.

（1）模型中参数的标定及其依据如表1所列.

为确保求解结果的稳定性，本文进行10次优化模型的求解运算.将10次求解结果取算术平均值

（2）求解结果与分析.

经过分析比较，案例求解结果在初始种群规模为100，迭代次数为2 000次的情况下得到了较好的结果.适应度收敛曲线如图2所示.

表1 案例参数取值情况Table 1 Value of parameters in the case study

图2 适应度收敛曲线Fig 2 Convergence curves of fitness function

模型优化结果与既有排班计划的对比如表2所列.

表2 模型优化结果与既有排班计划效率比较Table 2 Efficiency comparisons between the improved model and existing method

通过表2中优化结果与既有排班计划比较可知，优化模型获得的乘务排班计划值乘时间成本降低1.99%，值乘时间均衡程度和夜间休息时间均衡度的改善显著，优化率分别为11.87%和61.09%.

案例中20个乘务班次的早班值乘时间、白班值乘时间、晚班值乘时间，夜班值乘时间和夜间休息时间5项指标的既有排班计划和模型优化结果数据对比如图3（a）至（e）所示.

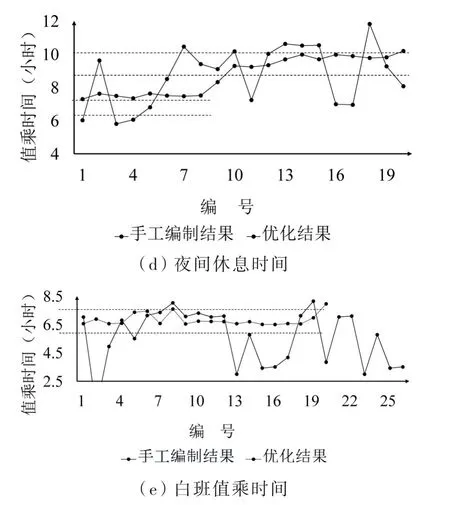
图3 既有排班计划值乘班次数据与优化结果比较Fig.3 Comparisons the detailed results from the improved model and existing method

从图3可知，优化模型得到20个乘务班次的晚班值乘时间、夜班值乘时间、夜间休息时间和白班值乘时间的均衡度与既有排班计划相比显著改善；早班值乘时间的均衡度略有下降，但并不显著，表明本文所构建模型总体上改善了乘务排班计划的各项均衡度指标.此外，既有排班计划需要安排26个班次才能完成值乘任务，通过优化模型获得的乘务排班计划则仅需20个班次就能完成相同的值乘任务，明显提高了值乘任务的安排效率.

6 研究结论

根据城市轨道交通乘务排班计划工作的实际需要，考虑了值乘区段的间隔时间、各班次的值乘时间、夜间休息时间等影响排班计划时间均衡度的因素，构建了基于时间均衡度的排班计划优化模型，采用遗传算法对模型进行了求解.以实际城市轨道交通线路的乘务排班工作为例，应用所建模型在既有运行图基础上进行排班计划优化研究，并将优化结果与既有排班计划进行了对比分析，获得以下结论.

（1）基于时间均衡度的排班计划优化模型可有效提高排班计划的时间均衡度.通过案例研究可知，排班计划时间成本降低了1.99%，值乘时间均衡度提高了11.87%，夜间休息时间均衡程度提高了61.09%，所需乘务班次数量减少6个.

（2）对不同班次（早班、晚班、白班、夜班）值乘时间的分析可知，优化模型总体上改善了乘务排班计划的效率与值乘时间均衡度，但部分班次优化效果不显著，在后续研究工作中需要进一步改善.

[1] 褚飞跃，田志强，倪少权.高速铁路单循环乘务排班计划编制模型与算法[J].铁道学报，2012,34(7):1-9. [CHU F Y,TIAN S Q,NI S Q.Model and algorithm for formulation of the single cycle crew rostering plans of high-speed railways[J].Journal of the China Railway Society,2012,34(7):1-9.]

[2] 王莹，刘军，苗建瑞.客运专线乘务交路计划编制的优化模型与算法[J].铁道学报，2009,31(1):15-19. [WANG Y,LIU J,MIAO J R.Modeling and solving the crew scheduling problem of passenger dedicated line[J]. Journal of the China Railway Society,2009,31(1):15-19.]

[3] Steinzen I,Gintner V,Suhl L,et al.A time-space network approach for the integrated vehicle-and crewscheduling problem with multiple depots[J]. Transportation Science,2010,44(3):367-382.

[4] Mesquita M,Paias A.Set partitioning∕covering-based approaches for the integrated vehicle and crew scheduling problem[J]. Computer & Operations Research,2008,35(5):1562-1575.

[5] 张增勇，毛保华，杜鹏，等.基于惩罚费用的城市轨道交通乘务排班优化模型与算法[J].交通运输系统工程与信息，2014,14(2):113-120.[ZHANG Z Y,MAO B H,DU P,et al.Urban rail transit crew scheduling model and algorithm based on punishment costs[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(2):113-120.]

[6] 李献忠，徐瑞华.基于时间耗费的城市轨道交通乘务排班优化[J].铁道学报，2007,29(1):21-25.[LI X Z, XU R H.Optimization of crew scheduling for urban rail transportation based on time costs[J].Journal of the China Railway Society,2007,29(1):21-25.]

[7] 李献忠，徐瑞华.基于乘务广义费用的城市轨道交通排班[J].同济大学学报，2007,35(6):750-754.[LI X Z, XU R H.An optimal wide crew-related costs-based scheduling for crew of urban rail transportation[J]. Journal of Tongji University(Natural Sciense),2007,35(6):750-754.]

[8] Zaepfel G,Boegl M.Multi-period vehicle routing and crew scheduling with outsourcing options[J]. International Journal of Product Economics,2008,113 (2):980-996.

[9] Jutte S,Albers M,Thonemann U W,et al.Optimizing railway crew scheduling at DB schenker[J].Interfaces, 2011,41(2):109-122.

[10] 胡思继.列车运行图编制理论[M].北京:中国铁道出版社，2007.[HU S J.Theory of train diagram[M]. Beijing:China Railway Press,2007.]

[11] 银大伟.乘务计划编制系统的研究与设计[D],西南交通大学，2008.[YIN D W.Research and design of crew scheduling system[D]. The Southwest Jiaotong University,2008.]

[12] Yunes T H,Moura A V,de Souza C C.Hybrid column generation approaches for urban transit crew management problems[J].Transportation Science,2005, 39(2):274-288.

Time Equitability-based Crew Scheduling Optimization for Urban Rail Transit

FENG Fu,CHEN Shao-kuan,DU Peng
(The MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology,Beijing Jiaotong University, Beijing 100044)

Crew scheduling of urban rail transit system,whose quality have a significant influence on the operational efficiency of urban rail transit,is an important part of urban rail transit operational management. This paper imports equilibrium as the indicator assessing the reasonability of the whole crew’s shift and rest in given period with minimum cost,on the basis of which an improved model for crew scheduling is established.Then in order to take into count the best match of shifts and the proper combination of morning and night shifts synchronously,the solution for the model is disassembled into two consistent phases that refers to the greedy algorithm and bi-direction matching method.Finally,this model is applied in the case study of the urban rail transit system in Beijing and achieves a better performance compared to the existing crew scheduling solution.As a result,the improved model upgrades effectively the time equitability of the crew scheduling.

urban traffic;urban rail transit;optimization model;genetic algorithm;crew scheduling;time equitability

2014-06-21

2014-09-11录用日期：2014-09-27

国家重点基础研究发展计划（2012CB725406）；国家自然科学基金项目（71131001）；北京市科技新星计划（Z121106002512028）.

丰富（1990-），男，湖北黄冈人，硕士生. *

shkchen@bjtu.edu.cn

1009-6744(2014)06-0164-07

U268.6

A