基于层级选址模型的区域客运枢纽布局优化研究

李婷婷，宋 瑞，何世伟，黎浩东

（北京交通大学a.城市交通复杂系统理论与技术教育部重点实验室;b.交通运输学院，北京100044）

基于层级选址模型的区域客运枢纽布局优化研究

李婷婷a，宋 瑞*b，何世伟b，黎浩东b

（北京交通大学a.城市交通复杂系统理论与技术教育部重点实验室;b.交通运输学院，北京100044）

为提高客运交通系统的运行效率，分析不同类型客运需求与各等级枢纽间的关系，考虑不同层次枢纽服务能力的约束，构建了基于层级选址模型的区域客运枢纽分层布局优化模型，使用CPLEX优化软件求解，最后设计算例验证了模型和算法的有效性.结果表明，与不分层的中位模型相比，分层模型能得到可达性更高的布局方案，考虑最大、最小服务能力约束后可达性有所下降，但更符合实际.面对客运需求的增长，枢纽规划部门应适当进行枢纽扩能和布局优化调整.

系统工程；布局优化；层级选址模型；客运枢纽；CPLEX

1 引 言

合理的客运枢纽布局，有利于构建高效的客运系统，从而更好地满足日益增长和日趋多样化的客运需求.客运枢纽布局优化问题属于分层设施选址问题，不同类型的客运需求由不同等级的客运枢纽为其服务.国外针对分层设施选址问题提出了层级选址模型，并广泛应用到医疗卫生、产品布局、教育系统、通信网络方面.Sahin等[1]对层级选址模型进行了研究综述；Galvao等[2]提出了容量限制的三层母婴医院选址基本模型，并以设施负荷平衡和需求加权距离最小为目标构建双目标模型；Teixeira等[3]提出了容量限制的嵌套型分层中位模型，并分析了单一分配、最近分配和路径分配约束的影响；Mestre等[4]考虑医院的分层和转送服务特性，提出医院重新选址模型；Chen等[5]提出了资金限制的三层避难场所规划模型.国内对区域客运枢纽布局的研究较少，刘强等[6]提出了区域综合交通枢纽布局双层规划模型；丁金学等[7]运用最大覆盖模型对中国交通枢纽进行了布局优化和分析；李代坤[8]将交通枢纽划分等级后运用中位模型分别对各等级枢纽进行布局优化.现有研究缺乏不同等级枢纽和不同客运需求关系的考虑，没有反映客运枢纽层级系统的本质特性.本文充分考虑不同等级客运枢纽和不同客运需求的关系，提出考虑能力限制的基于层级选址模型的区域客运枢纽布局优化方法，以期为区域客运枢纽布局提供决策参考.

2 区域客运枢纽等级划分

参考《综合交通网中长期发展规划》，根据城市的自然地理条件、功能定位、交通网络和客运发展情况、服务范围，将区域客运枢纽划分为全国性、区域性和地方性客运枢纽.另外，根据出行范围对客运需求进行分类，主要分为国际客流、省际客流、省域城际客流、市域客流.其中，不同类型客运需求使用的交通方式不同：国际客流主要为航空和水路；省际客流以铁路、航空、水路为主，公路为辅；省域城际客流以公路、城际轨道为主，航空、水路为辅；市域客流主要为城市公共交通.

如表1所示，各等级枢纽具有不同的服务范围、服务对象和衔接方式.全国性枢纽服务范围最广，地方性枢纽服务范围最小.全国性枢纽主要服务国际和省际客流，同时具有服务省域城际客流和市域客流的功能.区域性枢纽主要服务省域城际客流，地方性枢纽主要服务市域客流.尽管区域性枢纽具有服务省际客流的功能，地方性枢纽具有服务省际客流和省域城际客流的功能，但其相应服务能力非常小，远远不能满足本地相应类型需求，仅作为辅助功能.可见，不同客运需求对各层次客运枢纽服务能力有不同要求，服务能力的具体数值应结合城市具体情况确定.全国性枢纽要求具有较大的国际、省际客流服务能力；区域性枢纽要求具备较大的省域城际客流服务能力，同时具备少量的省际客流服务能力；地方性枢纽要求具备较大的市域客流服务能力，同时具有较少量的省际、省域城际客流服务能力.

表1 客运枢纽等级划分Table 1 Hierarchy system of passenger hub

3 区域客运枢纽分层布局优化模型

3.1 问题描述

区域客运枢纽分层布局可以描述为：对给定的区域，已知其中各城市各类型客运需求量、城市间的距离，以及各节点城市各层次服务能力最大值、最小值，同时给出若干重要交通节点城市作为枢纽备选点，从中选择最优的交通节点城市作为不同等级的枢纽，以满足区域内各城市不同类型客运需求并实现需求加权距离最小化.

3.2 模型构建

假设需求点和备选枢纽点同在城市的中心，同一需求点同一类型需求分配到同一枢纽.

集合定义如下：H表示需求点的需求类型、枢纽点的服务层次和枢纽等级的集合，H={1，2，3}；I表示需求点的集合，以i为索引；J表示所有备选枢纽点的集合，以j为索引.

参数定义如下：

k——需求点的需求类型、枢纽点的服务层次；

t——枢纽等级；

dij——需求点i和枢纽点j的距离；

uik——需求点i第k层的需求量；

cjk——若在枢纽点j设立枢纽，该枢纽点承担的第k层需求量至少达到的值（下文称为服务能力最小值）；

Cjk——枢纽点j能提供的第k层服务的最大能力（下文称为服务能力最大值）；Dk表示第k层需求的用户能接受的需求点到枢纽的最远距离.

变量定义如下：

xijk——如果需求点i第k层需求由枢纽点j服务，xijk=1，否则为0；

yjt——如果枢纽点j被选中为t级枢纽，yjt=1，否则为0；

wjk——枢纽点j承担的第k层需求量.

有能力约束的单分配区域客运枢纽分层布局模型如下（CHPM）：

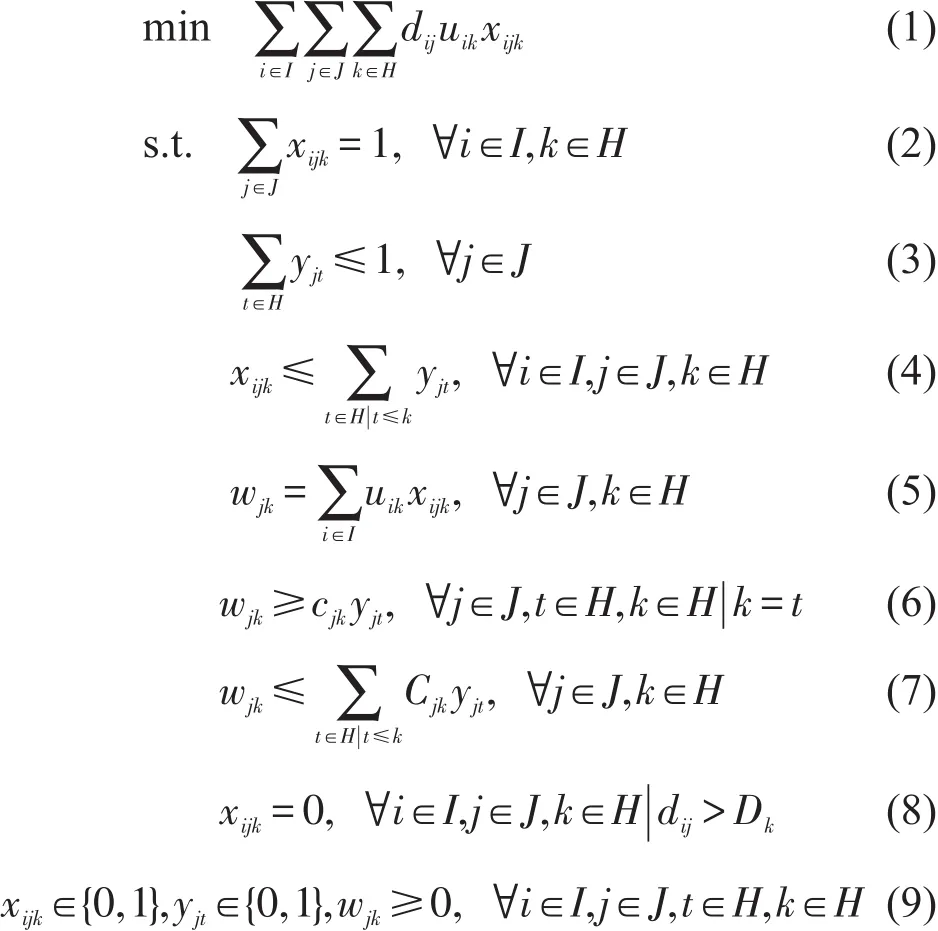
式(1)表示需求加权距离最小化，即可达性最大化.式(2)表示所有需求点的需求都得到满足.式(3)表示任何枢纽点都不允许同时设立不同等级的枢纽.式(4)表示需求点任一类型的需求必须由相同或更高等级的枢纽服务（1级为高级，3级为低级，由于低级枢纽的高层次服务功能仅为辅助功能，能力非常小而远远不能满足本地相应类型的需求，故忽略不计）.可以这样理解：当xijk=0，式(4)显然成立；当xijk=1，则时式(4)成立，表示若需求点i的第k类需求由枢纽点j服务，枢纽点j设立的枢纽中至少有一个其等级t与需求类型k相等或者更高.式(5)表示枢纽承担的任一类型的需求量等于由该枢纽点服务的所有需求点的对应类型的需求量之和.式(6)表示枢纽最高层次服务量的最小值必须小于其承担的相应类型的需求量.式(7)表示枢纽承担的任一类型的需求量必须在其对应层次服务的最大能力范围内.式(8)表示如果枢纽点离需求点的距离在可接受范围之外，需求点不由该枢纽点服务.式(9)表示变量的取值范围约束.

上述模型与有能力限制的分层中位模型[3]相比，充分考虑了区域客运枢纽布局的特点，同时对不同层次服务的能力分别进行约束，而文献[3]则对枢纽所有层次总服务能力之和进行限制.具体而言，各枢纽点任何层次服务的能力均有限，枢纽承担的各类型交通需求均应在枢纽各层次服务的最大能力范围内，而由于枢纽功能有所侧重，只要求其承担的最高层服务量超过相应值，而低层次服务量不作最小能力限制.

3.3 模型求解

上述模型为混合整数线性规划模型，可以采用CPLEX优化软件求解.

4 算例分析

4.1 算例数据

图1为研究区域，其中包含A-M城市13个，作为需求点.各城市间的距离如表2所示，城市各类型需求量及其服务能力最大值、最小值如表3所示.其中A-E作为1级枢纽备选点，而A-I作为2级枢纽备选点.由于1级枢纽为全国客流服务，覆盖范围设为500-600 km；2级枢纽主要服务区域客流，覆盖范围设为250-300 km；而3级枢纽主要服务本市客流，覆盖范围设为50-100 km.

图1 研究区域需求点分布Fig.1 Demand centers of the studied area

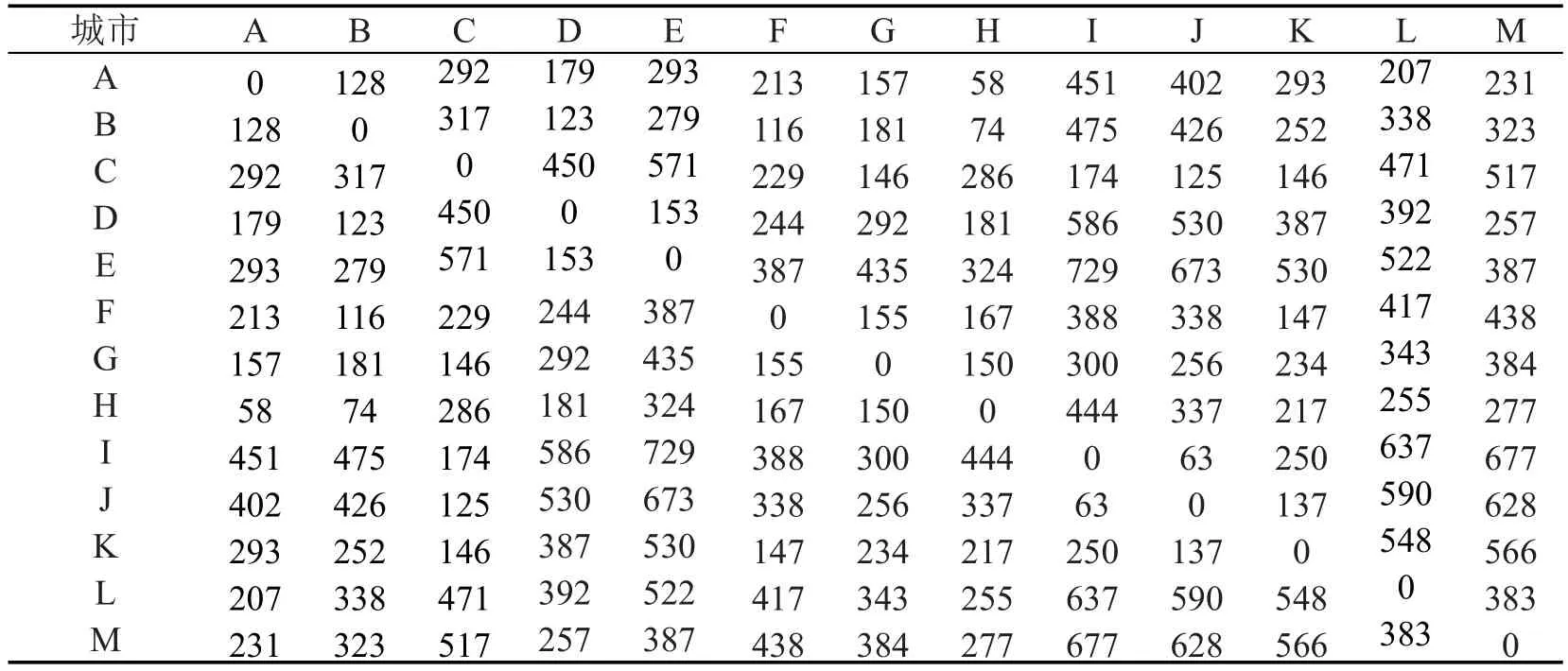
表2 各城市间的距离Table 2 Distances between cities （km）

表3 城市各类型需求量及其服务能力最大值、最小值Table 3 Demand of all types and capacity constraint parameters of all cities （万人次/年）

4.2 求解结果与比较

(1)求解结果.

在Intel Core i5-2450M CPU@2.50GHz，内存2G，操作系统Windows7环境下，使用优化软件CPLEX12.2，每次求解运行时间均少于5 s，求解得到不同枢纽覆盖范围下枢纽布局和需求分配方案，如图2所示.

1级枢纽和3级枢纽覆盖范围的变动对枢纽布局和需求分配影响不大，因为区域半径小于500 km，城市半径小于50 km.2级枢纽覆盖范围由300 km变为250 km时，G由2级枢纽变为3级枢纽，M的2级需求原来由D服务变为由A服务，因为MD间距离超过了250 km，同时G的2级需求原来由H服务变为由C服务.可见，覆盖范围影响的大小与城市之间的距离密切相关.

(2)模型比较.

如表4所示，本文模型（CHPM）与其他模型求得的布局方案均不相同，原因在于各种方法的机理不一样.模型non-HPM（即不分层的中位模型，使用中位模型分别对各级枢纽进行布局）没有对客运需求进行分类，对不同客运需求进行统一分配，且先确定高等级枢纽布局后确定下一级枢纽布局，没有同时考虑各级枢纽与客运需求之间的对应关系，其目标函数值远大于其他两种方法.模型UCHPM（即不考虑能力约束的分层中位模型）由于没有能力限制，需求点均分配到最近的枢纽点，故目标函数值比本文模型小，但实际情况中，枢纽各层次服务能力有限，此方法得到的方案中，一些枢纽承担客流量会超过枢纽的最大服务能力，与实际情况不相符，且会出现某些枢纽承担客流虽较少却仍然开通的情况，不符合规模经济的要求.本文模型（CHPM）充分考虑各级枢纽和不同需求的对应关系，反映了枢纽层级系统的本质特性，而由于最大、最小服务能力的约束，尤其在最大服务能力较小、最小服务能力较大的情况下，部分客运枢纽可能不符合最近分配，故得到的布局方案需求加权距离比UCHPM大.另外，在不同的枢纽覆盖范围下，其他模型布局方案均相同，而本文模型（CHPM）求解得到不同的布局方案，对枢纽覆盖范围敏感性更高.综上所述，本文模型比不分层的中位模型得到可达性更高的方案，而考虑能力约束后可达性有所下降但更符合实际，更能反映枢纽等级系统的特点.

图2 不同枢纽覆盖范围下的枢纽布局和需求分配Fig.2 Hub location and demand assignment at different coverage of hubs

表4 本文模型与其他模型的求解结果比较Table 4 Comparison of the results of model in this paper and other models

4.3 参数灵敏度分析

(1)服务能力最小值灵敏度.

图3为1、2、3级枢纽覆盖范围分别为500 km、300 km、100 km时，不同服务能力最小值对应的最优布局方案的需求加权距离.由于服务能力最小值取值越小，式(6)越容易满足，开通枢纽个数趋向于越多，而枢纽本身的需求由自己满足，因此需求加权距离越小.然而由于需求点各级需求只分配到单一枢纽，枢纽承担的客流量与需求点各级需求量密切相关，当服务能力最小值在承担的需求量内变化时，不会导致布局方案的改变.可见，服务能力最小值作为枢纽开通与否的重要依据，其取值对枢纽布局和分配方案有重要影响，需结合等级划分和规模经济设置，不宜过大或过小.

图3 不同服务能力最小值约束下的目标函数值Fig.3 Objective function values under various minimum capacity

(2)服务能力最大值灵敏度.

当1、2、3级枢纽覆盖范围分别为500 km、300 km、100 km时，C城市服务能力最大值从10 965降低到9 384后，K的1级需求由C服务变为由B服务（更远），目标函数值从5 773 996增加到5 994 794，枢纽布局与分配方案如图4(a)所示.C城市服务能力最大值从10 965增加到16 448后，G的1级需求由A服务变为由C服务（更近），目标函数值从5 773 996降低到5 743 614，枢纽布局与分配方案如图4(b)所示.可见，如果服务能力最大值足够大，需求点均能实现最近分配，此时对应的目标函数值更小.

图4 不同服务能力最大值约束下枢纽布局方案Fig.4 Hub location under different maximum capacity

结合服务能力最小值和最大值的灵敏度，当需求点需求增加而枢纽服务能力最小值不变时，式(6)可能会从不满足变为满足，该需求点有可能变为枢纽，或服务于该需求点的枢纽变为更高等级的枢纽.当需求增加较多而服务能力最大值不变，且最近的枢纽不能满足所有需求，则在单分配情况下，需求会被分配到更远的枢纽，导致目标函数增加.因此，需求增加会对枢纽布局产生影响，枢纽规划部门应根据客流变化，适当进行枢纽扩能和布局优化调整.

5 研究结论

本文对区域客运枢纽和客运需求进行分级和分类，分析了客运需求与枢纽的对应关系，考虑枢纽各层次服务最大、最小能力的限制，构建了基于层级选址模型的区域客运枢纽分层布局优化模型，并用CPLEX优化软件求解.通过与不分层的布局方法（即使用中位模型分别对各级枢纽进行布局）对比，该模型能反映枢纽层级系统的特性，得到可达性更高的枢纽布局方案，而考虑最大、最小能力约束则更能贴近实际，体现需求变化对枢纽布局的影响.面对客运需求的变化，枢纽规划部门应对枢纽做出适当的扩能和布局调整.设计求解大规模问题的有效算法，考虑不同需求的多分配和需求不确定性，制定更符合实际和鲁棒性强的枢纽布局方案，是有待深入研究的方向.

[1] Sahin G,Sural H.A review of hierarchical facility location models[J].Computers&Operations Research, 2007,34(8):2310-2331.

[2] Galvao R D，Espejo L GA，Boifey B，et a1．Load balancing and capacity constraints in a hierarchical location model[J]． European Journal of Operational Research，2006(2):63l-646．

[3] Teixeira J C,Antunes A P.A hierarchical location model for public facility planning[J].European Journal of Operational Research,2008,185(1):92-104.

[4] Mestre A M,OliveiraM D,Barbosa-PóvoaA. Organizing hospitals into networks:A hierarchical and multiservice model to define location,supply and referrals in planned hospital systems[J].OR Spectrum, 2012,34(2):319-348.

[5] Chen Z F,Chen X,Li Q,et al.The temporal hierarchy of shelters:A hierarchical location model for earthquakeshelter planning[J]. International Journal of Geographical Information Science,2013,27(8):1612-1630.

[6] 刘强,陆化普,王庆云.区域综合交通枢纽布局双层规划模型[J].东南大学学报(自然科学版),2010(6): 1358-1363.[LIU Q,LU H P,WANG Q Y.Bi-level programming model for regional integrated transportation hub layout[J].JournalofSoutheast University(Natural Science Edition),2010(6):1358-1363.]

[7] 丁金学,金凤君,王成金,等.中国交通枢纽空间布局的评价、优化与模拟[J].地理学报,2011(4):504-514. [DING J X,JIN F J,WANG C J,et al.Evaluation, optimization and simulation of the spatial layout of transport hubs in China[J].Acta Geographica Sinica, 2011(4):504-514.]

[8] 李代坤.综合交通枢纽城市级节点布局优化研究[D].北京:北京交通大学,2011.[LI D K.Integrated transportation hub layout[D].Beijing:Beijing Jiaotong University,2011.]

[9] Weaver J R,Churc,R L.The nested hierarchical median facility location model[J].Infor,1991(29):100-115.

Regional Passenger Hub Layout Optimization Based on Hierarchical Location Model

LI Ting-tinga，SONG Ruib，HE Shi-weib，LI Hao-dongb
(a.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology; b.School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China)

To improve the efficiency of the passenger transport system,a model for regional passenger hub layout is proposed.The relationship between different passenger hub and passenger transport demand is analyzed.A hierarchical model with capacity constraints is built and solved by CPLEX.Numerical example is given to validate the model.The results show that hierarchical model is superior to non hierarchical median model for accessibility.In addition,the minimum and maximum capacity constraints lead to accessibility decline yet make the model more realistic.Hub planning department should expand the capacity of hubs and adjust hub layout in the face of the passenger transport demand increase.

system engineering;layout optimization;hierarchical location model;passenger hub;CPLEX

2014-05-06

2014-06-30录用日期：2014-07-10

国家重点基础研究发展计划资助课题（2012CB725403）.

李婷婷（1985-），女，广东鹤山人，博士生. *

rsong@bjtu.edu.cn

1009-6744（2014）06-0036-06

U491

A