铝合金复合管连续挤压包覆成形本构方程的建立和数值模拟

闫观海，赵升吨，张德海，郭俊行，王增宝

（1．西安交通大学 机械工程学院，西安 710049；2．郑州轻工业学院 机电工程学院，郑州 450002）

铝合金复合管连续挤压包覆成形本构方程的建立和数值模拟

闫观海1，赵升吨1，张德海2，郭俊行1，王增宝1

（1．西安交通大学 机械工程学院，西安 710049；2．郑州轻工业学院 机电工程学院，郑州 450002）

基于等温热压缩实验，分别获得了AA3003铝合金在变形温度为20～300℃，AA4343铝合金在变形温度为300～450℃，应变速率为0．01～1 s－1条件下的真实应力应变曲线，建立了AA4343铝合金的本构方程．采用DEFORM－2D软件，以AA3003为芯材，AA4343为包覆材料，分析了复合变形区长度、挤压速度和坯料温度对连续挤压包覆过程的影响．结果表明：随着复合变形区长度的减小，连续挤压包覆成形稳定时芯管的径向受力随之降低，合适的复合变形区长度为2．0mm；随着挤压速度的增加，芯管出现了不同程度的变形，合适的挤压速度为0．1 mm/s；随着坯料温度的升高，芯管所受到的径向力随之减小，合适的温度范围为400～500℃．

连续挤压包覆；AA3003铝合金；AA4343铝合金；本构方程；数值模拟

随着汽车工业的发展，对汽车零部件的轻量化要求越来越高，汽车空调散热器的轻量化研究成为一个热点．铝合金复合管是空调散热器的主要组成材料，该材料目前主要依靠国外进口，国内对于铝合金复合管生产新工艺的研究尚处于空白阶段．

连续挤压包覆技术（CONCLAD）以其产品的连续性，技术稳定性和节省能源成为线缆生产工业中最具发展潜力的方法之一［1］．CONCLAD利用连续挤压原理可以实现双金属复合，并能克服前拉挤压法间歇工作的缺点．芯材穿过挤压模，挤压靴上有防止坯料泄漏的槽封块，槽封块与旋转的挤压轮凹槽组成一个动态的挤压容室，坯料由挤压轮的凹槽通过摩擦力进入挤压容室，挤压力由坯料与挤压轮凹槽之间的摩擦来形成，坯料进入模腔后与芯线复合形成复合线．

国内外学者对复合管连续挤压包覆成形技术进行了大量研究［2－4］．Etherington［5］对连续挤压过程进行了定性分析，将挤压轮凹槽内部坯料的变形区域分为挤压夹持区和初始夹持区，得到了两个区域长度的近似关系式．Maddock等人［6］基于连续挤压过程中变形的特点，假设材料的剪切应力取决于应力分布，得出剪切面之间速度出现线性减少的趋势．Tirosh等人［7］采用能量法和工程近视法对连续挤压成形过程进行了实验研究和理论推导，得出了坯料与挤压轮的接触面压力分布、载荷作用位置、靴座包角等对相关工艺参数的影响．宋宝韫等人［8］将挤压轮槽内部的变形区域分为咬合区、镦粗区、充满区和挤压区四个区域，分析了相应区域的速度场分布和应力场分布，根据屈服条件得出咬合区、镦粗区和充满区接触应力的表达式．储灿东等人［9］运用DEFORM软件，对连续挤压各个阶段任意时刻材料的内部状态进行模拟，建立连续挤压成形过程的摩擦驱动力学模型，获得如等效应力、等效应变、流动速度场、温度场分布、剪应力等．彭岳林等人［10］认为现行的连续挤压变型腔设计的不合理性导致了能量的无效损耗和金属塑性体回流，提出了一种连续挤压雏形管变形腔的模型，依据变分上限原理对此模型的上限功率进行求解．

本文在Gleeble－1500热模拟实验机上对AA3003铝合金、AA4343铝合金进行了等温压缩实验，研究了上述两种合金在不同变形温度和不同应变速率范围内的流变力学行为，建立了AA4343铝合金的本构方程．采用DEFORM－2D软件，以AA3003铝合金为芯材，AA4343铝合金为包覆材料，对铝合金复合管连续挤压包覆成形进行了数值模拟，研究了复合变形区长度、挤压速度和坯料温度对连续挤压包覆过程的影响．

1 热模拟实验

在数控动态热力学物理模拟试验机Gleeble－1500上进行AA4343和AA3003材料的等温压缩实验．AA3003选取20、120、200和300℃，AA4343选取300、350、400和450℃，选取0．01、0．1和1 s－1三种应变速率，总应变量为0．7（真应变）［11］．得到两种材料在不同条件下的真应力－真应变曲线，如图1．

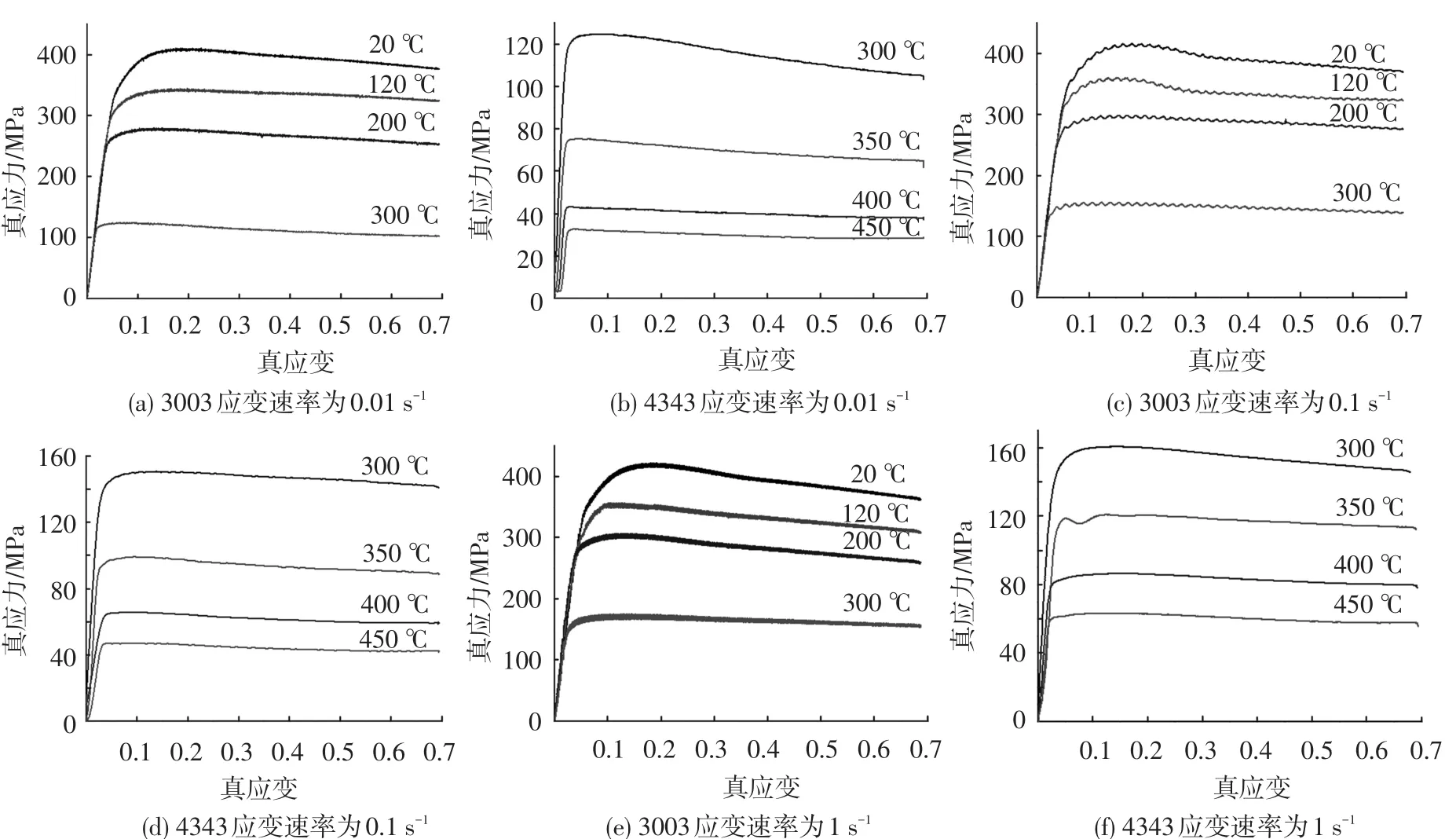
图1 AA3003和AA4343热压缩变形真应力－真应变曲线

从图1看出，AA4343的真应力先随应变的增大而迅速升高，出现一个峰值后逐渐下降至稳态值，呈现稳态流变的特征；在同一应变速率下，真应力随变形温度的升高而明显下降；在同一变形温度下，真应力水平随应变速率的增加而升高，说明AA4343在该实验条件下具有真的应变速率敏感性．AA3003的真应力也随变形温度的升高而明显下降，但对应变速率敏感性较差．

2 本构方程的构建

金属的热压缩变形可视为蠕变在大应变速率和较高应力水平的一种延伸，两者有着非常相似的变形和软化机制，从而金属的热压缩变形可用高温变形时的真应力－真应变之间的关系描述［12］．在变形过程中，金属的应变速率和温度T之间的关系可用参数Z表示，即Zener－Hollomon表示［13－14］，

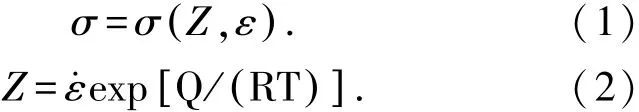
由文献［15］，Z与σ服从以下关系，

式中，A1，A2为结构因子；α为应力水平参数；n为应力指数；β为应变参数．

且α，β，n之间满足以下关系，

式（2）结合式（3）、（4）得出，低应力水平下，

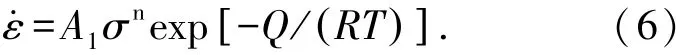
在高应力水平下，

对式（6）和（7）两边取对数可得，

Sellar和Tegar在式（6）和（7）的基础上提出了一种包括热变形激活能Q和温度T在所有应力的双曲正弦形式修正的Arrhenius关系式［16］，

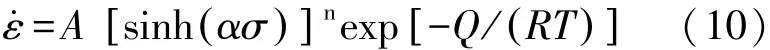
式中，A为结构因子．

对图2中的两个关系式进行线性回归处理，得到在不同温度下AA4343铝合金热压缩变形过程中的参数α，n和β的数值，见表1．在不同温度下α与不同变形条件下的峰值真应力σ相乘得到相应变形条件下的ασ值见表2．当应变速率为0．01 s－1、变形温度大于300℃时，变形属于低应力水平下的变形，符合式（8）；当应变速率为1 s－1时，变形属于高应力水平下的变形，符合式（9）．由式（8）和（9）可知，当应变速率一定时，nR/Q和βR/Q可用lnσ－1/T曲线和σ－1/T曲线的斜率表示，通过一元线性回归进行处理，可分别得到lnσ－1/T的关系曲线和σ－1/T的关系曲线，如图3．

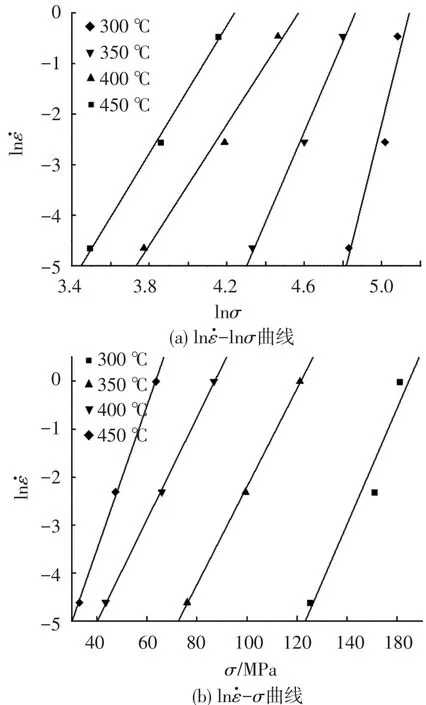
图2 AA4343铝合金热压缩变形时应变速率与流变应力关系

表1 不同温度下AA4343铝合金的热压缩变形参数

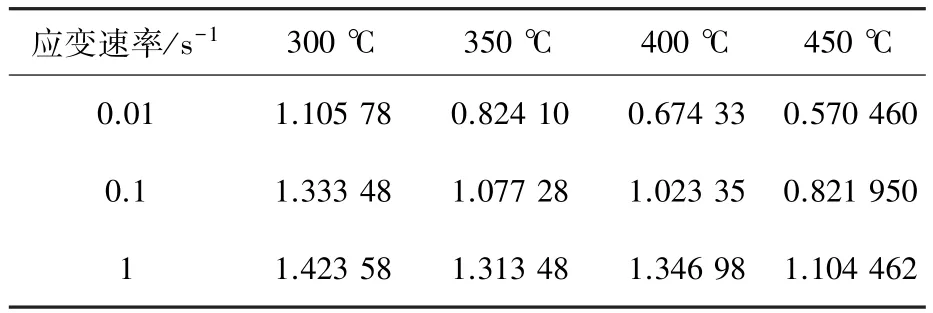
表2 不同变形条件下的ασ值

将一元线性回归得到的斜率代入式（5）得

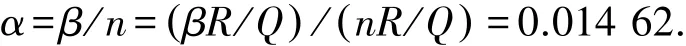
对式（9）取自然对数得

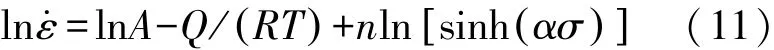
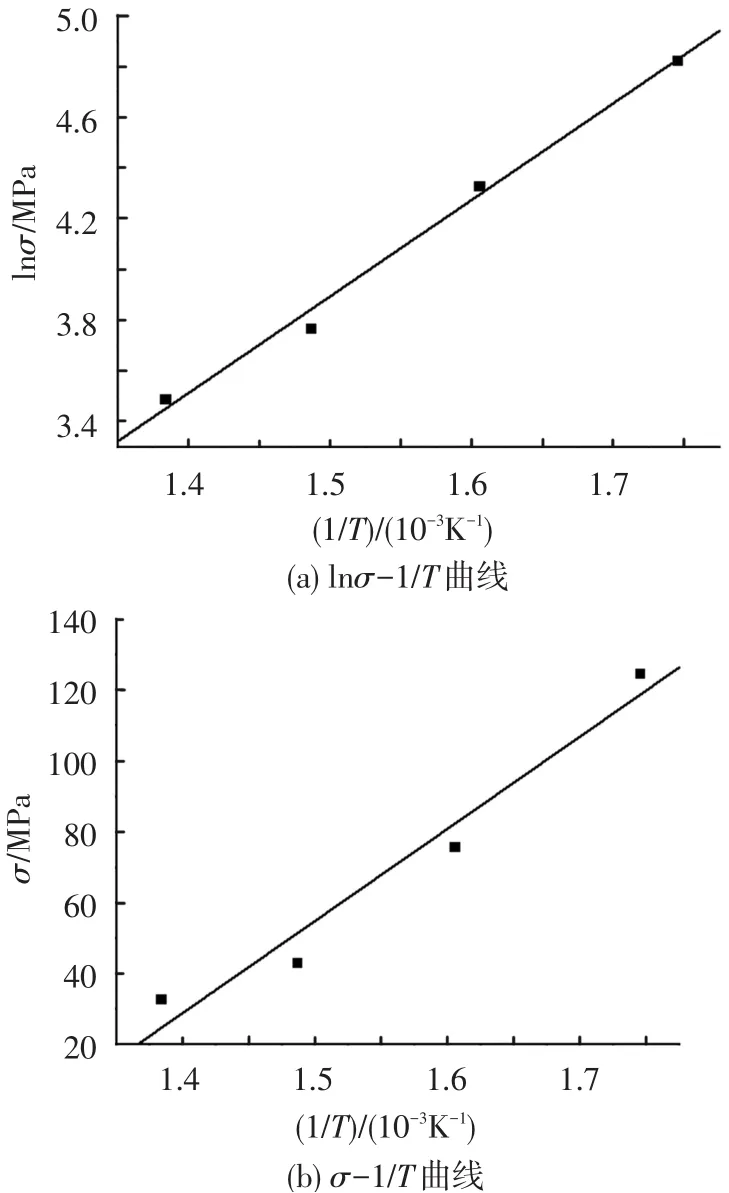
图3 AA4343铝合金压缩变形时流变应力与变形温度的关系

对式（11）微分得

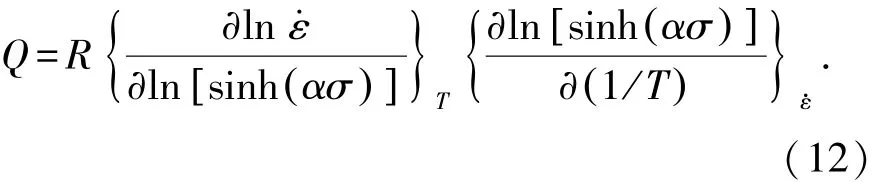
将图4中所得各直线的斜率代入式（12），得到不同变形温度下的变形激活能，取其平均值得

将式（10）代入式（2）得到

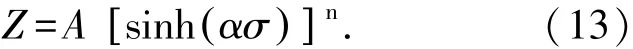
对式（13）取自然对数得

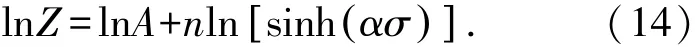
将Q＝254．574 kJ·mol－1代入式（2）得

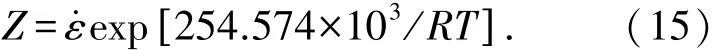
将不同变形温度下铝合金的热变形应变速率代入式（15）得到不同的Z值，再与对应的峰值真应力一起代入式（14），用最小二乘法线性回归，绘制相应的ln Z－ln[ sinh(ασ)]曲线，如图5．

由图5可知ln A和n分别为ln Z－ln[ sinh(ασ)]关系曲线中的截距和斜率，其中ln A＝42．359 3，n＝6．241 52，求得A＝2．491 21×1 018．可见AA4343铝合金流变应力双曲正弦值的自然对数和Z参数的自然对数满足线性关系，因此可以用包含Arrhenius项的Z参数描述AA4343铝合金高温压缩变形的流变行为．

将求得的参数代入式（10），可得AA4343热压缩变形的本构方程为

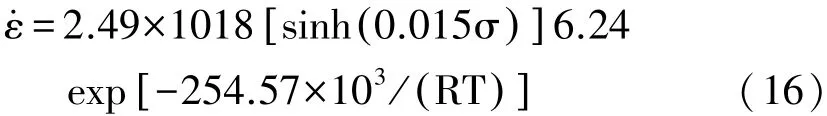
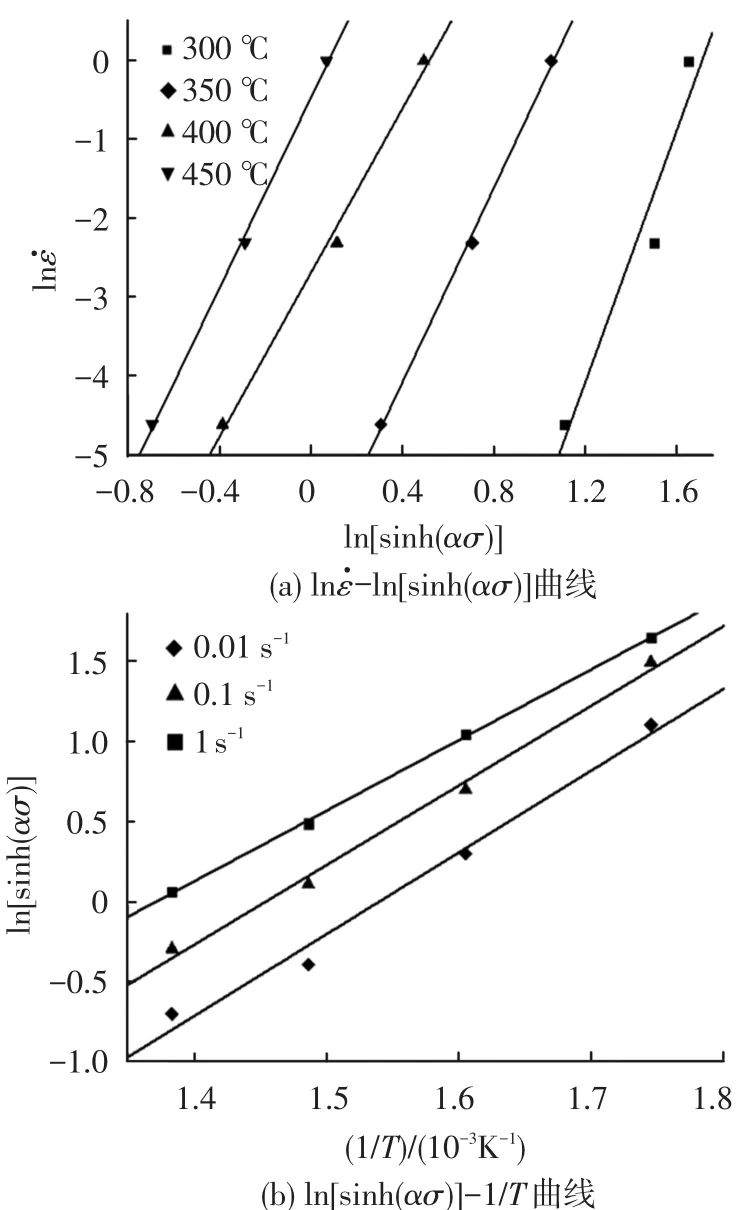
图4 AA4343热压缩应变速率与流变应力的关系

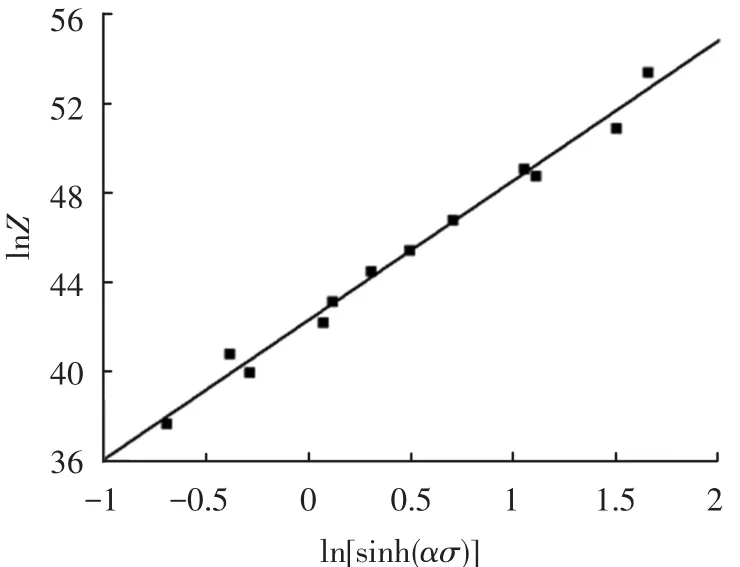
图5 流变应力与Z参数的关系

3 二维数值模拟

3．1 二维几何模型的建立与单元离散

用DEFORM－2D进行模拟，模具和挤压腔材料选择H13刚体，芯管和包覆材料用刚塑体，芯管用AA3003，包覆材料用AA4343．在DEFORM－2D软件的材料库中，有H13钢的材料特性，可以直接选取．对于AA4343和AA3003，可将热模拟实验获得的材料特性数据，输入DEFORM－2D软件的材料库，以便模拟求解时调用．

连续挤压包覆成形的模具有凸模和凹模两部分组成，简化模型如图6．

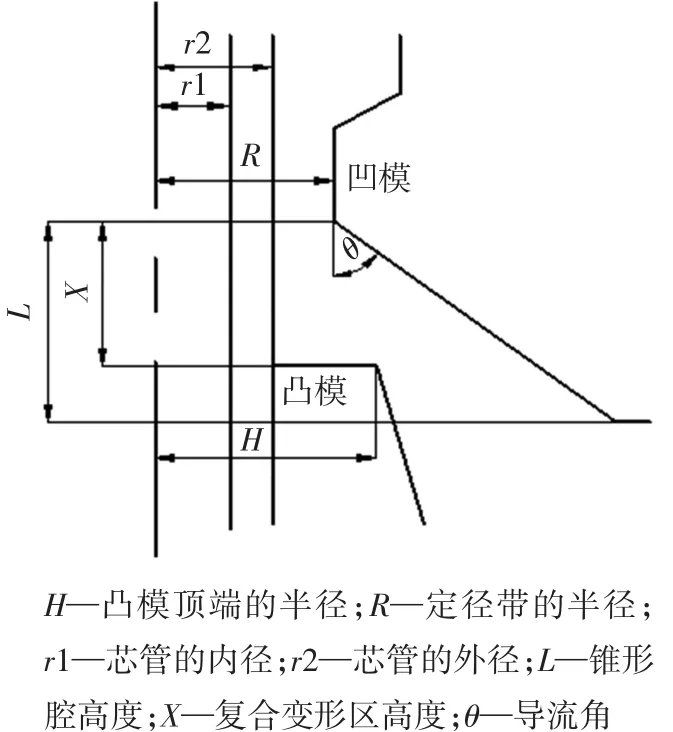
图6 模具的简化模型

3．2 复合变形区长度对连续挤压包覆过程的影响

按照表3选取了5组复合变形区长度，研究对连续挤压包覆过程的影响．其余模拟参数：θ＝60°；L＝5 mm；r1＝7．5 mm；r2＝9．5 mm；R＝10 mm；f＝0．3；V＝0．1mm/s．应用DEFORM－2D模拟得到图7．

表3 复合变形区长度模拟几何参数选取

从图7（a）看出复合变形区长度为0．8 mm时，连续挤压包覆成形达到稳定状态时，挤压腔依然没有被坯料充满；坯料进入挤压型腔时的最小截面积等于包覆层的截面积，坯料无法在挤压型腔内形成积累，不能形成足够的静水压力．当坯料在挤压过程中接触到芯管后，在二者之间的摩擦力的互相作用下，坯料会带动芯管沿成品出口方向移动，但由于这种摩擦力比较小，不能达到稳定的无相对滑动的状态，包覆管材会出现“脱骨”缺陷．从图7（b）看出，变形区长度为1．0 mm时，坯料不能在挤压包覆腔内形成积累，挤压出的成品也会出现缺陷．从图7（c）和图7（d）看出，当坯料刚进入挤压包覆腔时就快速充满挤压包覆腔，形成稳定的包覆状态，说明复合变形区长度对连续挤压包覆成形过程影响很大．

图7 复合变形区不同长度的挤压包覆成形过程

从模拟结果还可以看出，复合变形区长度对芯管破坏（变形或断裂）有一定的影响．当复合变形区的长度为0．8、1．0、1．5和2．0 mm时，没有出现芯管变形或者断裂的情况，随着长度的增加，芯管变形和断裂的几率变大；当复合变形区的长度为3．0mm时，发现连续挤压包覆成形过程中芯管发生变形（图7（e）），这种情况下的成品是不合格的产品，因此复合变形区长度对成品的质量有影响．

复合变形区长度对坯料和芯管结合强度的影响．从图7（c）和图7（d）的模拟结果对比看出，两者都可以得到合格的产品，究竟哪种情况相对更好？需要比较两种模拟结果的芯管受力．从图8知，X＝2．0 mm时连续挤压包覆成形稳定状态时芯管径向受压力约为8．66 kN，而X＝1．5 mm时芯管受力为5．24 kN，由此可见X＝2．0 mm时模拟结果在没有产生产品破坏情况的基础上要比X＝1．5 mm的模拟结果获得更好的界面结合强度．

图8 复合变形区长度为1．5 mm和2．0 mm的芯管径向受力图

3．3 挤压速度对连续挤压包覆过程的影响

按照表4分别选取了3组挤压速度，研究它对连续挤压包覆过程的影响．其余模拟参数：θ＝60°；L＝5mm；r1＝7．5 mm；r2＝9．5 mm；R＝10 mm；X＝2．0 mm；f＝0．3．

表4 模拟过程中挤压速度的选取

在研究挤压速度对包覆过程的影响时排除了一些耦合因素（如温度效应）的影响，以便更好的表现三种挤压速度对连续挤压包覆过程的影响，如图9．从挤压速度分别为0．1、0．5、1．0mm/s时连续挤压包覆过程的模拟结果看出，当速度为0．5和1．0 mm/s时在坯料充满型腔后芯管出现了不同程度的变形．随着挤压速度的增加，芯管将会出现不同程度的变形，挤压速度越大，芯管的变形越大，这是由于速度越大，芯管的径向受力就越大，从而导致芯管变形变大．因此，当挤压速度为0．1 mm/s时，对于挤压包覆比较有利，能得到较好的包覆产品．

图10为三种不同挤压速度下连续挤压包覆成形过程中的芯管径向变形分布图，从图中可以看出，随着挤压速度的增加，在复合变形区位置的芯管变形不断增大，由此可知选V＝0．1 mm/s合适．

图9 不同挤压速度对包覆成形过程的影响

图10 不同挤压速度下芯管径向变形

3．4 坯料温度对连续挤压包覆过程的影响

按表5选取6组坯料温度，研究它对连续挤压包覆过程的影响．其余模拟参数：L＝5mm；r1＝7．5mm；r2＝9．5mm；R＝10mm；X＝2．0mm；f＝0．3；θ＝60°；V＝0．1mm/s．

表5 数值模拟中温度参数的选取

坯料温度是连续挤压包覆成形技术的主要工艺参数，为此考虑了不同温度的坯料对连续挤压包覆过程的影响，图11是坯料温度分别为20、250、300、350、400和500℃时坯料对芯管变形的影响，从图中可以看出，坯料温度较低时，随着连续挤压包覆成形过程的进行，芯管由于受到坯料的挤压力很大而发生变形，但是随着坯料温度的增加，芯管变形逐渐减小，当温度达到400℃以上时，芯管几乎没有发生变形．由于温度再升高会逐渐接近坯料的熔点，从而不能形成稳定的包覆，因此把挤压温度确定在400～500℃．

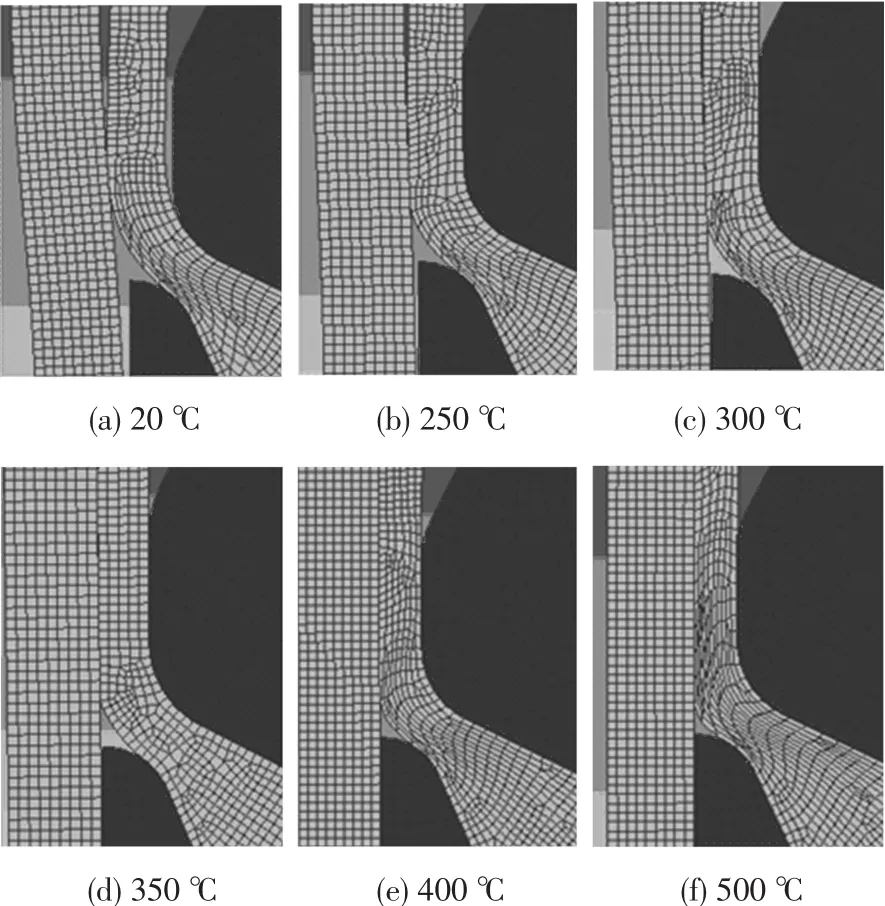
图11 不同坯料温度下的连续挤压包覆过程

4 结 论

1）基于等温热压缩实验，获得了AA4343铝合金在变形温度为300～450℃，应变速率为0．01～1 s－1条件下的真实应力应变曲线，建立了能够表征该合金热变形行为的本构方程：·ε＝2．49× 1 018[ sinh(0．015σ)]6．24exp[－254．57×103/(RT)]．

2）通过改变复合变形区的长度，分析了它对连续挤压包覆成形过程的影响，得到了连续挤压包覆成形达到稳定状态时芯管径向受力分布．通过分析可以看出随着复合变形区长度的减小，连续挤压包覆成形稳定时芯管的径向受力随之降低，合适的复合变形区长度为2．0 mm．

3）选择了三组挤压速度，研究了它对连续挤压包覆成形过程的影响，得出随着挤压速度的增加，芯管出现了不同程度的变形，合适的挤压速度为0．1 mm/s．

4）通过分析坯料温度对连续挤压包覆成形过程的影响可知，随着坯料温度的升高，材料的变形抗力会逐渐降低，因此芯管所受到的径向力也会随之减小，但温度也不宜过高，合适的温度范围为400～500℃．

［1］钟毅．连续挤压技术及其应用［M］．北京：冶金工业出版社，2004．ZHONG Yi．Continuous extrusion technology and its applicaiton［M］．Beijing：Metallurgical Industry Press，2004．

［2］李峰，林俊峰，张鑫龙，等．连续变截面直接挤压成形技术研究［J］．材料科学与工艺，2012．20（5）：55－59．LIFeng，LIN Junfeng，ZHANG Xinlong，etal．Research on continuous variable cross⁃section direct extrusion（CVCDE）［J］．Materials Science＆Technology，2012．20（5）：55－59．

［3］VASILE D C，NICOLAE S，DOINA R，et al．Micro⁃structural observations of fracture surfaces for a 6063－T1 ECAP processed aluminum alloy［J］．UPB Scien⁃tific Bulletin，Series B：Chemistry and Materials Sci⁃ence，2010，72（4）：163－172．

［4］张德海．板料成形过程回弹的三维检测与评价方法研究［J］．材料科学与工艺，2012．20（4）：128－133＋139．ZHANG Dehai．3D measuring and evaluated method of springback in sheetmetal forming［J］．Materials Sci⁃ence＆Technology，2012．20（4）：128－133＋139．

［5］ETHERINGTON C．Conform－A New Concept for the Continuous Extrusion Forming ofMetals［J］．Journalof Engineering for Industry，1974，（8）：893－900．

［6］MADDOCK B．Aluminlum［J］．1978，54（3）：207－211．

［7］TIROSH J．Theoretical and Experimental Study of the CONFORM Mertal Forming Proeess［J］．Transaction of ASME，1978．

［8］李明典，宋宝韫，杨鑫华，等．连续挤压轮槽塑性变形区应力分析及几何参数的确定［J］．塑性工程学报，1999，6（3）：25－30．LIMingdian，SONG Baoyun，YANG Xinhua，et al．Stress analysis and determination of geometry parame⁃ters in plastic zone of wheel groove for continuous ex⁃trusion［J］．Journal of Plasticity Engineering，1999，6（3）：25－30．

［9］储灿东．连续挤压过程的3D计算机仿真和光塑性仿真［D］．上海：上海交通大学，2001．CHU Candong．Three⁃dimensional computer and photo⁃plastic simulation of continuous extrusion forming process［D］．Shanghai：Shanghai Jiaotong University，2001．

［10］彭岳林，刘红卫．连续挤压变形腔的改进及其上限分析［J］．中南工业大学学报，1998，29（1）：94－96．PENG Yuelin，LIU Hongwei．The improvement of de⁃formation chamber of continuous extrusion forming and the analysis of upper bound［J］．Journal of Central South University of Technology，1998，29（1）：94－96．

［11］蔡一鸣，李慧中，梁霄鹏，等．7039铝合金高温的热变形行为［J］．中国有色金属学报，2008，18（10）：1775－1780．CAIYiming，LI Huizhong，LIANG Xiaopeng，et al．Thermal deformation behavior for 7039 aluminum alloy at elevated temperature［J］．The Chinese Journal of Nonferrous Metals，2008，18（10）：1775－1780．

［12］李俊鹏，沈健，许小静，等．7050高强铝合金高温塑性变形的流变应力研究［J］．稀有金属，2009，33（3）：318－322．LI Junpeng，SHEN Jian，XU Xiaojing，et al．Flow stress of7050 high strength aluminum alloy during high temperature plastic deformation［J］．Chinese Journal of Rare Metals，2009，33（3）：318－322．

［13］SRIVATSAN T S，KOLAR D，MAGNUSEN P．Influ⁃ence of temperature on cyclic stress response，strain resistance，and fracture behavior of aluminum alloy 2524［J］．Materials Science and Engineering A，2001，314：118－130．

［14］SPIGARELLIS，EVANGELISTA E，MCQUEEN H J．Study of hotworkability of a heat treated AA6082 alu⁃minum alloy［J］．Scripta Materialia，2003，49：179－183．

［15］RAMANATHAN S，KARTHIKEYAN R，DEEPAK K V，et al．Hot deformation behavior of 2124 aluminum alloy［J］．Mater．Sci．Technol，2006，22（5）：611－615．

［16］吴文祥，孙德勤，曹春艳，等．5083铝合金热压缩变形流变应力行为［J］．中国有色金属学报，2007，17（10）：1667－1671．WU Wenxiang，SUN Deqin，CAO Chunyan，et al．Flow stress behavior of 5083 aluminum alloy under hot compression deformation［J］．The Chinese Journal of Nonferrous Metals，2007，17（10）：1667－1671．

（编辑 张积宾）

The establishment of constitutive equation and numerical simulation of CONCLAD for alum inum alloy tube

YAN Guanhai1，ZHAO Shengdun1，ZHANG Dehai2，GUO Junhang1，WANG Zengbao1

（1．School of Mechanical Engineering，Xi′an Jiaotong University，Xi′an 710049，China；2．Mechanical and Electrical Engineering Institute，Zhengzhou University of Light Industry，Zhengzhou 450002，China）

The true stress⁃true strain curves of AA3003 and AA4343 aluminum alloy in the temperature range of 20～300℃and 300～450℃，and in the strain rates range of 0．01～1 s－1，were obtained by isothermal hot compression tests，and then the constitutive equation of AA4343 aluminum alloy was established．The influence of different processing parameters，such as length of clad forming zone，billet temperature and extrusion velocity，on the process of CONCLAD which select 3003 aluminum alloy as the core material and 4343 aluminum alloy as the claddingmaterial was investigated with DEFORM－2D．The results show that the radial force of the core tube decreases as the length of clad forming zone increases during the steady state of CONCLAD process．With the increasing of extrusion velocity，the core tube exhibits deformation to different extent．With the increasing of billet temperature，the radial force of the core tube decreases．According to the analysis above，the optimal process parameters，such as length of clad forming zone 2．0 mm，extrusion velocity 0．1 m/s and billet temperature 400～500℃，are obtained．

CONCLAD；3003 aluminum alloy；4343 aluminum alloy；Numerical simulation

TP391；TG806

A

1005－0299（2014）02－0104－08

2012－11－13．

国家自然科学基金面上项目（50975222）；高等学校博士学科点专项科研基金项目（20100201110002）；河南省重点科技攻关项目（142102110151）；河南省基础与前沿技术研究项目（132300410181）；郑州市科技攻关项目（131PPTGG411－T）；郑州轻工业学院博士科研基金资助项目．

闫观海（1974－），男，博士；

赵升吨（1962－），男，教授，博士生导师．

张德海，E⁃mail：zhangdehai0318＠163．com．