基于Radau伪谱法的制导炸弹最优滑翔弹道研究

袁宴波,张科,薛晓东

(1.西北工业大学航天学院,陕西西安 710072;2.中国空空导弹研究院第12研究所,河南洛阳 471009)

基于Radau伪谱法的制导炸弹最优滑翔弹道研究

袁宴波1,2,张科1,薛晓东2

(1.西北工业大学航天学院,陕西西安 710072;2.中国空空导弹研究院第12研究所,河南洛阳 471009)

基于Radau伪谱法求解最优控制问题的原理,研究了滑翔型制导炸弹的最大射程优化问题。对制导炸弹动力学模型进行了无量纲化处理,结合极小值原理推导了最优控制轨迹的解析解和一阶必要性条件,采用Radau伪谱法将弹道优化问题转化为非线性规划问题,基于协态映射原理给出了数值解的最优性验证方法。仿真结果表明,Radau伪谱法能够提供具有工程应用价值的最优解,与常规的最大升阻比滑翔弹道相比,优化后的弹道射程增加10%以上。

兵器科学与技术;滑翔制导炸弹;弹道优化;Radau伪谱法

0 引言

当前,相当多的制导炸弹采用了大升阻比气动外形设计,如美国的JDAM-ER、SDB,中国的LS-6等。此类滑翔型制导炸弹具有很强的滑翔能力,因此射程较远,可以实现防区外对地精确打击。由于制导炸弹本身没有动力,仅能依靠投放高度势能和投放初速度动能来实现较远的滑翔距离。采用怎样的弹道规划策略才能实现最远的滑翔距离,是一个具有现实意义的问题。最常用的弹道规划方案是将弹道划分为滑翔段和俯冲攻击段(如图1所示):在滑翔段按照最大升阻比对应的攻角来进行飞行控制,在俯冲攻击段按照比例导引的形式进行弹道控制。然而,这种弹道规划方案只是一种经验上的方法,并不是理论上的最优结果。

图1 滑翔型制导炸弹常规弹道示意图Fig.1 Conventional trajectory of glide guided bomb

实际上,制导炸弹的弹道优化问题可以归结为带有状态约束和控制约束的非线性最优控制问题,其求解方法一般分为间接法和直接法[1]。间接法基于 Pontryagin极值原理将最优控制问题转换成Hamiltonian两点边值(HBVP)问题,其优点是能够满足一阶最优性必要条件,能够精确求得协态变量和控制变量。但是由于保证HBVP问题收敛的协态变量没有物理意义,其初值很难估计,同时还存在收敛半径小,对初始值敏感等问题,HBVP的求解是非常困难的。直接法是采用参数化方法将连续空间的最优控制问题转化成非线性规划(NLP)问题,而NLP问题有很多成熟的数值解法。由于直接法对状态微分方程进行了离散化,因此由直接法求得的协态变量和控制变量精度比间接法稍差。

伪谱法是最近发展的一类求解最优控制问题的方法,该方法融合了间接法和直接法的优点:不仅能够获得最优控制问题的数值解,而且可以提供协态变量的精确信息[2]。因而伪谱法在最优控制问题的数值解法方面,特别是飞行器轨迹优化方面逐渐流行并成为研究热点。常见的伪谱方法包括:Legendre伪谱法(LPM)、Gauss伪谱法(GPM)以及Radau伪谱法(RPM)。文献[3]对上述3种方法的计算精度、计算效率等方面进行了比较研究,指出GPM和RPM精度相当,并且均略优于LPM,而在计算效率方面3种方法差别不大。文献[4]基于GPM对无人攻击机(UCAV)对地攻击武器的投放轨迹进行了优化计算;文献[5]利用GPM进行了助推-滑翔导弹的弹道优化研究。但是对于飞行器的轨迹优化问题,离散解的最优性验证在文献中还是很少见。

本文采用RPM来求解制导炸弹的最优滑翔弹道,基于极小值原理推导了问题的解析解和最优性一阶必要条件,同时基于协态映射原理[6]给出了数值解的最优性验证方法,并对数值解的最优性进行了比较全面的验证。

1 制导炸弹弹道优化模型

1.1 状态方程及其无量纲化

进行弹道优化时主要关注制导炸弹铅垂平面内的运动,不考虑地球自转的影响,并假定重力加速度g为常值,则制导炸弹的运动可用如下简化方程进行描述:

将以上各相对量(角度没有相对量形式)代入(1)式中得到无量纲化的状态方程:

下文为表述方便,省去式中的上标。在制导炸弹弹道优化问题中,仅考虑铅垂平面运动的情况下,炸弹运动轨迹的改变取决于攻角α,取控制量为攻角α.

1.2 过程约束

过程约束即炸弹在飞行过程中弹道参数必须满足的约束条件。一般地,由于弹体结构强度和操纵舵能力的限制,炸弹法向过载不能超过限制值。法向过载定义为

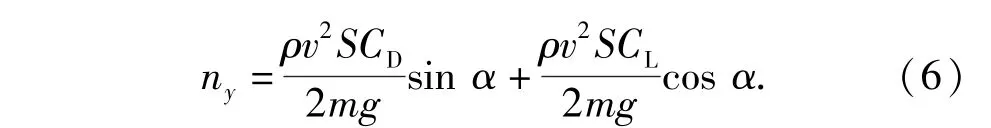
另外,炸弹飞行速度不能超出设计范围太多,因此,应满足弹道最小速度约束。同时,作为控制量的攻角必须在设计范围内变化,并且变化速率不能太快,故攻角的幅值和变化率受到上限约束。综上,过程约束如下:

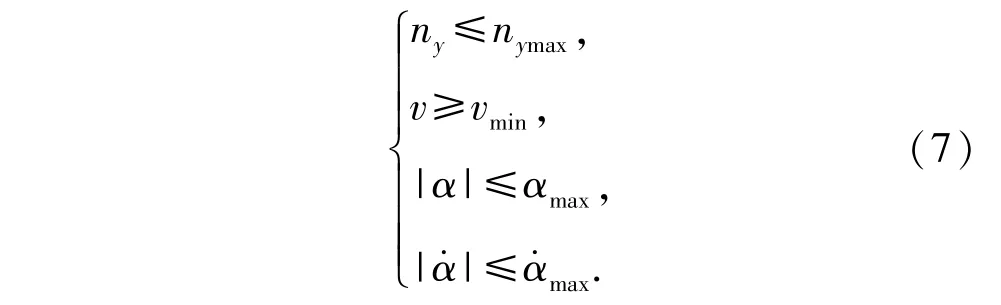
1.3 边界条件

边界条件包括初始边界条件和终端边界条件。初始边界条件即炸弹投放时刻状态变量的初值,是完全给定的,即

终端边界条件是指制导炸弹在弹道终点需满足的条件,通常有落地速度与落地弹道倾角的要求,即

1.4 性能指标

制导炸弹弹道优化的目的是增大射程,以x(tf)表示弹道终点处射程,射程取极大值等效为-x(tf)取极小值,故取性能指标为

1.5 最优控制的一阶必要条件

上述弹道优化问题对应的最优控制问题可描述为:在时间区间[t0,tf](其中tf自由)中,寻找最优控制变量α*(t),使(10)式中的性能指标J取极小值,并使状态变量[x,y,v,θ]T和控制变量α(t)满足状态微分方程(5)式、过程约束(7)式、边界条件(8)式和(9)式。

根据最优控制理论,上述最优控制问题的哈密顿函数为

本文将采用RPM求解上述最优控制问题,并验证伪谱法求得的结果满足最优性一阶必要条件。

2 RPM优化基本原理

RPM求解最优控制问题的基本原理为:将未知的状态变量和控制变量在一系列 Legendre-Gauss-Radau(LGR)点上离散化,构造全局插值多项式来逼近状态变量和控制变量,再通过对状态变量求导来代替动力学微分方程。这样,连续系统最优控制问题被转化为受一系列代数约束的NLP问题[7],可以采用数值方法求解。RPM离散最优控制问题的主要流程[8]如下。

2.1 时域变换

2.2 全局插值多项式近似状态变量和控制变量

用RPM处理连续时间最优控制问题时,需要在一系列LGR离散点上对控制变量和状态变量进行全局插值多项式逼近。控制变量在1,…,K-1个网格处用如下的Nk阶Lagrange多项式来逼近:

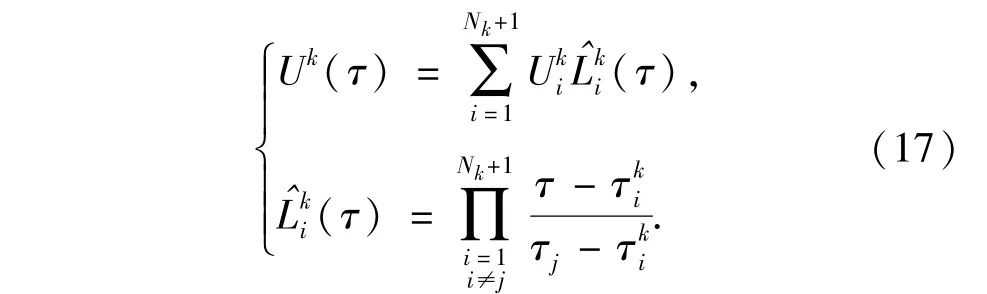
由于终端时间tf没被配置,第K个网格处的控制变量用Nk-1阶Lagrange多项式来逼近。类似地,状态变量在第k个网格处可以近似为

2.3 微分方程约束转换为代数约束

通过全局插值多项式近似状态变量后,状态变量的导数可通过对多项式求导来近似,从而将动力学微分方程转换为代数约束,即

将(19)式代入动力学微分方程,并在LGR点上进行离散,可得

2.4 离散后的性能指标及边界条件

采用LGR配置点离散化后,性能指标函数可近似表示为

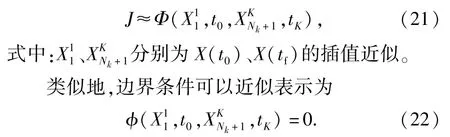
基于上述的数值近似方法,原连续最优控制问题被离散,并转换为NLP问题,转换所得的NLP问题可采用数值方法求解。其中,序列二次规划(SQP)是一种较好的选择,SQP算法较为成熟,在此不做介绍。

2.5 协态映射原理及最优性验证

对于最优控制问题,令PN为该问题经伪谱法参数化得到的NLP问题,N为用于近似的Lagrange多项式阶数。令Pλ为应用庞特里亚金极小值原理得到的边界值问题。Benson等[9]和 Huntington[10]的研究证明了PN问题的KKT(Karush-Kuhn-Tucker)条件与Pλ问题最优性条件之间的等价性,即NLP问题的KKT乘子与LGR节点上的协态变量值之间存在一一对应的关系,这就是伪谱法的协态映射原理。事实上,Fahroo等[11]指出,RPM对协态变量的估计由下式确定:

利用数值优化结果和伪谱法得到的协态变量估值,可以根据1.5节中最优控制的一阶必要条件得到最优控制轨迹的解析解,将其与全局插值多项式逼近得到的最优控制轨迹相比较,可以验证伪谱法的有效性。本文将根据实例仿真结果对此进行验证。

3 仿真验证与结果分析

3.1 仿真结果

某制导炸弹升阻比与速度和攻角的关系如图2所示。由图2可知,在各个飞行马赫数下,制导炸弹在攻角为5°时升阻比最大。因此,按照常规的弹道规划方案,要保持制导炸弹在滑翔段始终处于最大升阻比的飞行状态,只需要按照5°的攻角进行飞行控制即可。以下针对具体条件分析RPM优化算法的边界条件和约束条件,并将RPM优化结果与常规弹道进行对比。

图2 某制导炸弹升阻比与速度和攻角的关系Fig.2 Lift-to-drag ratio vs.angle of attack at different Mach numbers of a glide guided bomb

制导炸弹相关参数为:质量m=557 kg,参考面积S=0.116 m2,最大法向过载nymax为2g,弹道最小速度vmin=120 m/s;炸弹初始状态:投放高度y(t0)= 10 km,投放速度v(t0)=250 m/s;末端状态约束: y(tf)=0 m,v(tf)=270 m/s,θ(tf)=-80°;取xref= 10 km,vref=250 m/s,则RPM算法的边界条件为

按照(24)式和(25)式设定RPM优化算法边界条件及约束条件,优化后的状态变量和控制变量曲线如图3～图8所示,图中给出了与常规的最大升阻比滑翔弹道的对比情况。

图3 弹道曲线对比Fig.3 Trajectory vs.time

由图3可以看出,从炸弹投放后开始,RPM优化弹道就比常规弹道高度要高,且整体上弹道曲线更加平直,最终射程由81 km增大到92 km,增幅达13.5%.图4、图5表明在射程增大的同时,弹道飞行时间由435 s增加到513 s,并且在弹道末端两种方案均满足(24)式中的速度约束和弹道倾角约束。图6显示在弹道初始段和末段两种方案控制变量差别较大,而中段大部分时间RPM优化结果只是在常规方案附近波动,说明常规的最大升阻比方案作为一种简单易行的方案,仍具有一定的工程应用价值,但是如果追求发挥制导炸弹的射程极限,则RPM优化算法显示出优势。图7和图8表明在全弹道上(25)式的过程约束条件得到满足。

图6 攻角曲线对比Fig.6 Angle of attack vs.time

图7 法向过载曲线对比Fig.7 Normal overload vs.time

图8 攻角变化率曲线对比Fig.8 Angle of attack vs.time

3.2 最优性验证

按照(24)式和(25)式确定的边界条件及约束条件,经RPM优化算法得到的协态变量曲线如图9所示;由RPM优化算法得到的控制轨迹α(t)与通过最优性一阶必要条件得到的最优控制轨迹α*(t),如图10所示,RPM算法给出的哈密顿函数曲线如图11所示。

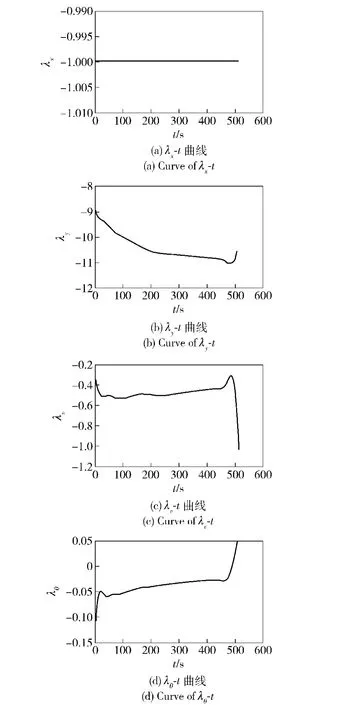
图9 RPM算法给出的协态变量曲线Fig.9 Co-states obtained from RPM optimization

由图9可以看出,横截条件(14)式得到满足;另一方面,由于经过无量纲化后各状态变量处于同一数量级,大大缩小了寻优范围,因而协态变量变化范围也不大。由图10可知,除个别地方由于控制约束限幅,RPM算法求得的控制变量轨迹与最优控制轨迹稍有差别外,二者轨迹完全重合。由前文的分析知,哈密顿函数沿最优轨线保持为0.由图11可见,哈密顿函数值在0附近波动,满足最优性一阶必要条件,充分说明了RPM算法求得的控制轨迹是最优的,算法是有效的。

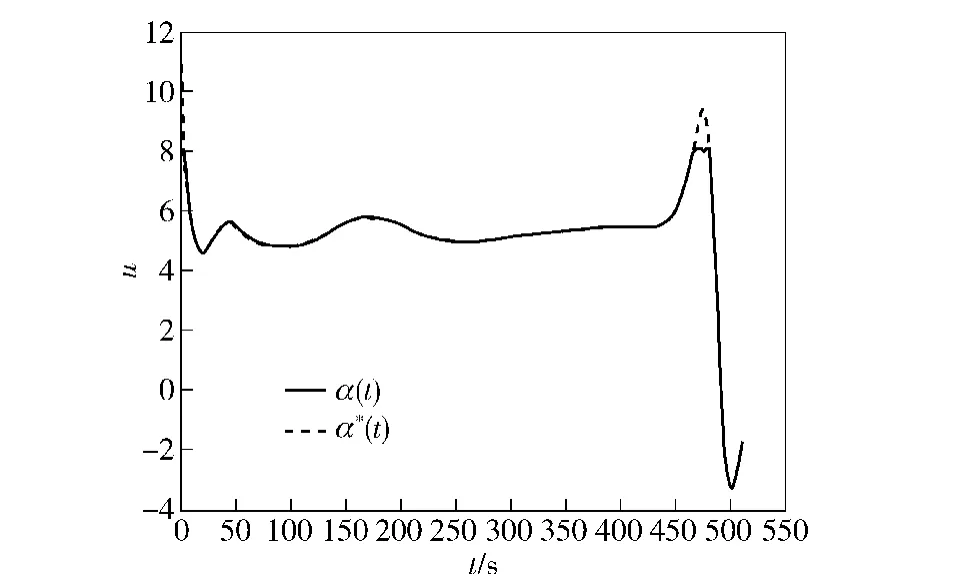
图10 RPM算法控制轨迹与一阶必要条件给出的控制轨迹对比Fig.10 Comparison of control trajectory obtained from RPM optimization and first-order necessary condition

图11 RPM算法给出的Hamilton函数曲线Fig.11 Hamiltonian function curve obtained from RPM optimization

3.3 工程应用分析

为了进一步说明RPM优化算法在增大制导炸弹射程方面的优势,分别对上述两种方案在不同初始条件下的弹道情况进行了仿真计算(末端边界条件和约束条件与(24)式和(25)式相同),仿真结果如表1所示。

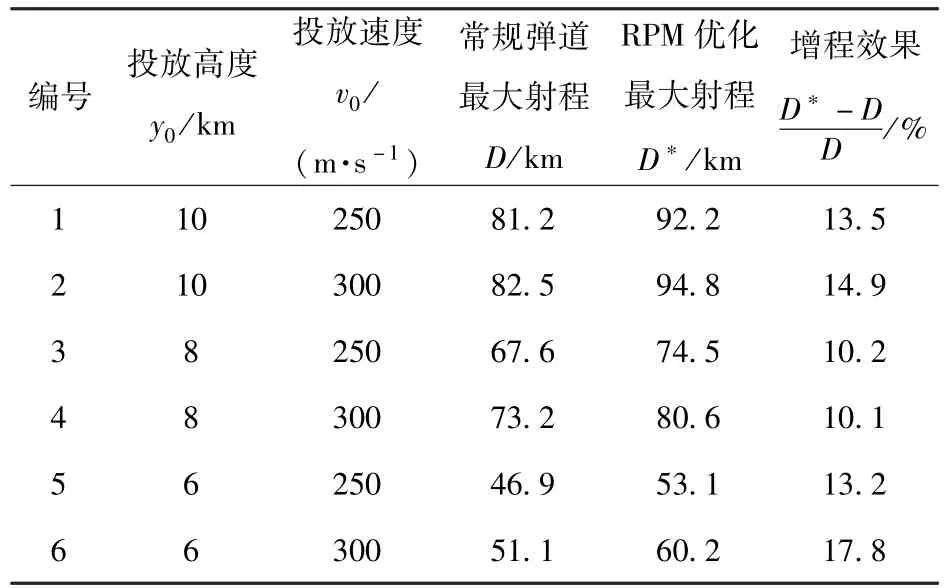
表1 不同初始条件下RPM优化算法增程情况Tab.1 The extended ranges obtained from RPM optimization under different initial conditions

从表1可以看出,与常规方案相比,在各种初始条件下,经RPM优化后制导炸弹最大射程均能得到显著增加,增程效果均在 10%以上,最高达到17.8%.另一方面,从工程实现的角度来讲,由于弹道优化工作可以事先离线完成,因此,可以将最优控制变量(即攻角)根据不同的飞行速度和高度进行拟合,然后将拟合后的参数表装定到弹上,炸弹投放后,由飞控计算机根据飞行条件实时插值得到最优飞行攻角,进而可以根据最优飞行攻角进行弹道飞行控制。与常规的最大升阻比方案相比,只是增加了最优参数表的装定和二维插值计算,占用弹载计算机资源不多,工程上完全可以实现。

4 结论

本文利用RPM对滑翔型制导炸弹的最优滑翔弹道进行了研究。对制导炸弹动力学模型进行了无量纲化处理,结合极小值原理推导了最优控制轨迹的解析解和一阶必要性条件。采用RPM将弹道优化问题转化为NLP问题,基于协态映射原理给出了数值解的最优性验证方法。仿真和分析结果表明:

1)无量纲化处理使各状态变量处于同一数量级,大大缩小了寻优范围;

2)采用RPM可以求得满足最优性一阶必要条件的数值解,并且能够准确地给出协态变量的估值;

3)与常规的最大升阻比滑翔弹道相比,采用RPM优化后的弹道增程效果超过10%.

本文的研究结果,对制导炸弹的增程设计具有工程应用价值,同时,对滑翔型制导炸弹的弹道规划及制导律设计也具有一定的参考价值。

References)

[1] John B T.Survey of numerical methods for trajectory optimization [J].Journal of Guidance,Control and Dynamics,1998,21(2): 193-206.

[2] Rao A V,Clarke K A.Performance optimization of a maneuvering reentry vehicle using a Legendre pseudospectral method[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit.California:AIAA,2002:1-13.

[3] Huntington G T,Benson D,Rao A V.A comparison of accuracy and computational efficiency of three pseudospectral methods[C]∥AIAA Guidance,Navigation and Control Conference and Exhibit. South Carolina:AIAA,2007:1-22.

[4] 张煜,张万鹏,陈璟,等.基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划[J].航空学报,2011,32(7):1240-1251.

ZHANG Yu,ZHANG Wan-peng,CHEN Jing,et al.Air-toground weapon delivery trajectory planning for UCAVs using Gauss pseudospectral method[J].Acta Aeronautica et Astronautica Sinica,2011,32(7):1240-1251.(in Chinese)

[5] 刘欣,杨涛,张青斌.助推-滑翔导弹弹道优化与总体参数分析[J].弹道学报,2012,24(3):43-48.

LIU Xin,YANG Tao,ZHANG Qing-bin.Trajectory optimization and parameter analysis for boost-glide missile[J].Journal of Ballistics,2012,24(3):43-48.(in Chinese)

[6] Garg D,Patterson M A,Darby C L,et al.Directtrajectory optimization and costate estimation of general optimal control problems using a Radau pseudospectral method[C]∥AIAA Guidance,Navigation and Control Conference.Chicago,Illinois:AIAA,2009: 1-29.

[7] Darby C L,Hager W W,Rao A V.Direct trajectory optimization using a variable low-order adaptive pseudospectral method[J]. Journal of Spacecraft and Rockets,2011,48(3):433-445.

[8] 王铀,赵辉,惠百斌,等.利用Radau伪谱法求解UCAV对地攻击轨迹研究[J].电光与控制,2012,19(10):50-53.

WANG You,ZHAO Hui,HUI Bai-bin,et al.Air-to-ground trajectory planning for UCAVs using a Radau pesudosprctral method [J].Electronics Optics&Control,2012,19(10):50-53.(in Chinese)

[9] Benson D A,Huntington G T,Thorvaldsen T P.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006, 29(6):1435-1440.

[10] Huntington G T. Advancementand analysisofa Gauss pseudospectral transcription for optimal control problems[D]. Massachusetts,US: MassachusettsInstituteofTechnology, 2007:51-57,115-143.

[11] FahrooF, Ross IM. Costateestimation by a Legendre pseudospectral method[J].Journal of Guidance,Control and Dynamics,2001,24(2):270-277.

Optimization of Glide Trajectory of Guided Bombs Using a Radau Pseudo-spectral Method

YUAN Yan-bo1,2,ZHANG Ke1,XUE Xiao-dong2
(1.School of Astronautics,Northwestern Polytechnical University,Xi'an 710072,Shaanxi,China; 2.No.12 Institute,China Airborne Missile Academy,Luoyang 471009,Henan,China)

The problem of optimizing the maximum range of a glide guided bomb is studied based on the principle of solving optimal control problems using the Radau pseudo-spectral method.The dynamic model of the guided bomb is nondimensionalized.Combining with the Pontryagin minimum principle,the analytic solution of the optimal control and the first-order necessary condition are derived.The trajectory optimization problem is translated to a nonlinear programming via the Radau pseudo-spectral method.Based on covector mapping principle,an optimality verification method is presented for the numerical solution. Simulation results show that the Radau pseudo-spectral method can provide a highly valuable optimal solution for engineering application.Compared with the conventional maximum lift-to-drag ratio gliding trajectory,the trajectory after optimization can be extended by more than 10%.

ordnance science and technology;glide guided bomb;trajectory optimization;Radau pseudo-spectral method

TJ765.5

:A

:1000-1093(2014)08-1179-08

10.3969/j.issn.1000-1093.2014.08.007

2013-09-10

袁宴波(1981—),男,博士研究生。E-mail:runble@163.com;张科(1968—),男,教授,博士生导师。E-mail:zhangke@mail.nwpu.edu.cn