弹丸卡膛规律影响因素分析

李淼,钱林方,陈龙淼,徐亚栋

(南京理工大学机械工程学院,江苏南京 210094)

弹丸卡膛规律影响因素分析

李淼,钱林方,陈龙淼,徐亚栋

(南京理工大学机械工程学院,江苏南京 210094)

为了研究弹丸卡膛参数对弹丸膛内运动初始条件的影响,对中大口径火炮弹丸卡膛过程进行分析。利用显式动力学有限元数值模拟方法对新型155 mm火炮弹带惯性卡膛过程进行了分析研究,综合考虑不同的卡膛速度、摩擦系数、身管仰角、初始卡膛姿态角、弹炮间隙对卡膛深度、卡膛力以及卡膛姿态的影响,得到了各个因素对卡膛结果的影响规律,其中卡膛速度、摩擦系数对卡膛深度和卡膛力有较大影响,而身管仰角和初始卡膛姿态角对卡膛姿态起到了较大的作用,弹炮间隙则对3个卡膛结果都有明显的影响,这些结论为弹药装填机的设计和揭示弹丸膛内运动规律提供参数依据。

兵器科学与技术;卡膛;有限元方法;卡膛结果

0 引言

弹丸卡膛是一个复杂的动力学过程。一定质量的弹丸,在卡膛速度的作用下与身管坡膛发生碰撞,在动量的作用下,弹带发生塑性变形,在弹带与坡膛之间形成残余塑性接触力和摩擦力,弹丸在这些力共同作用下可靠停留在坡膛(膛内)。其中弹带与身管坡膛接触瞬间的速度,称为卡膛速度。可靠的卡膛结果应能确保在任意仰角条件下,一组弹丸卡膛的轴向位置保持一致以及卡膛姿态保持相近,卡膛后在一定的外界干扰下弹丸不发生从坡膛上掉落和晃动等现象。

弹丸卡膛结果是弹丸装填的重要参数,决定了弹丸膛内运动最起始的状态,不同的卡膛结果会导致整个膛内运动过程的不一致。文献[1]认为卡膛速度不同对射击精度有较大的影响;文献[2]认为卡膛速度以及弹带身管之间的摩擦系数对弹丸最终的卡膛深度有着显著的影响;文献[3]认为弹丸在输弹过程中弹带会产生碰撞,这也会导致弹丸卡膛姿态不一致;文献[4]认为卡膛速度和卡膛力是供输弹系统设计的重要指标;文献[5]最早采用二维位置敏感探测器(PSD)技术对卡膛姿态进行了测量。

本文建立了弹丸卡膛的三维有限元模型,综合考虑卡膛速度、摩擦系数、身管仰角、初始卡膛姿态角以及弹炮间隙的影响,对卡膛过程进行了计算,在此基础上对卡膛结果的变化规律进行了研究。

1 卡膛过程弹塑性建模

1.1 基本假设

以某155 mm/52倍口径车载炮为例进行卡膛分析,在进行卡膛分析时,作如下基本假设:

1)坡膛为刚体,弹带与坡膛弹塑性碰撞过程中,坡膛不发生任何变形。

2)考虑弹带与坡膛间的摩擦,动摩擦系数为固定值μd.

3)弹丸本体为刚体,弹带与弹丸本体的结合为非完全的,碰撞过程中,结合面上可能会发生分离现象。

某155 mm榴弹弹带具体结构如图1所示。身管坡膛角为α,弹丸前定心部与身管阳线的半径差为弹炮间隙εg.

1.2 有限元模型的建立

弹带在身管坡膛处的卡膛有限元模型如图2所示,结构用三维实体等参元进行离散。弹带单元采用八节点六面体减缩积分单元,弹带外表面与身管产生滑动接触,故其划分比较细密;弹带内表面与弹丸本体接触,用接触单元来描述。身管为炮钢材料,其硬度远高于弹带材料的硬度,可以认为在卡膛过程中不变形,可用刚体单元进行离散简化。弹丸本体也采用刚体单元进行离散简化。对身管添加全约束,且分别在弹带与身管、弹带与弹丸本体、身管与弹丸之间添加接触。通过施加一与弹丸重力相等的固定作用力来模拟弹丸重力对碰撞过程的影响。当卡膛结束后,由于弹带发生塑性变形,在弹带与坡膛之间存在法向残余接触力和切向摩擦力,法向残余接触力和切向摩擦力在轴向的投影即卡膛力F.

弹带材料的等效屈服应力可采用经典的Johnson-Cook模型:

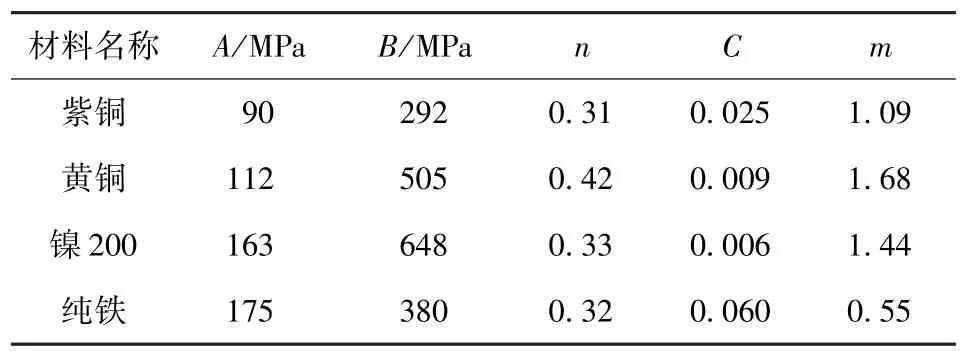
表1 4种弹带材料特性Tab.1 Material characteristics of several kinds of band

1.3 卡膛结果分析

弹带弹塑性卡膛原理可以表征为质量为m的弹丸,在卡膛速度u和动量mu作用下,弹丸以初始卡膛姿态角Φ1,通过弹带与身管坡膛发生弹塑性碰撞的动力学问题,其最终求解结果为弹丸的卡膛深度L、稳定卡膛姿态角Φ2和卡膛力F.卡膛深度L是指弹带与坡膛碰撞开始至碰撞结束过程中弹丸沿身管轴向的位移。弹体坐标系OCξηζ由弹丸质心平动坐标系OCx0y0z0按照3-2-1顺序旋转φ1、-φ2、γ 3个欧拉角得到。其中,弹丸姿态角可以表示为Φ=φ1+iφ2,如图3.Φ1、Φ2分别为卡膛过程中 Φ的初值和终值,Φ1=φ11+iφ12,Φ2=φ21+iφ22.

图3 弹丸姿态角示意图Fig.3 Sketch of projectile posture

图4为卡膛结束后弹丸与身管坡膛之间的接触受力图,图中Nf、Nr分别为坡膛对前、后弹带的法向作用力,卡膛力可以表示为下面形式:

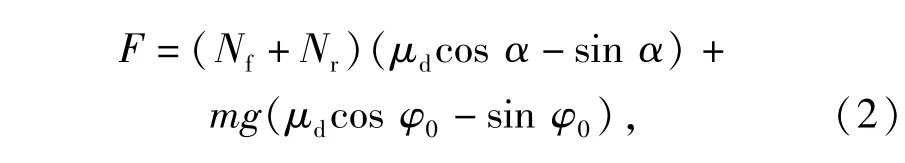
式中:φ0为身管仰角。

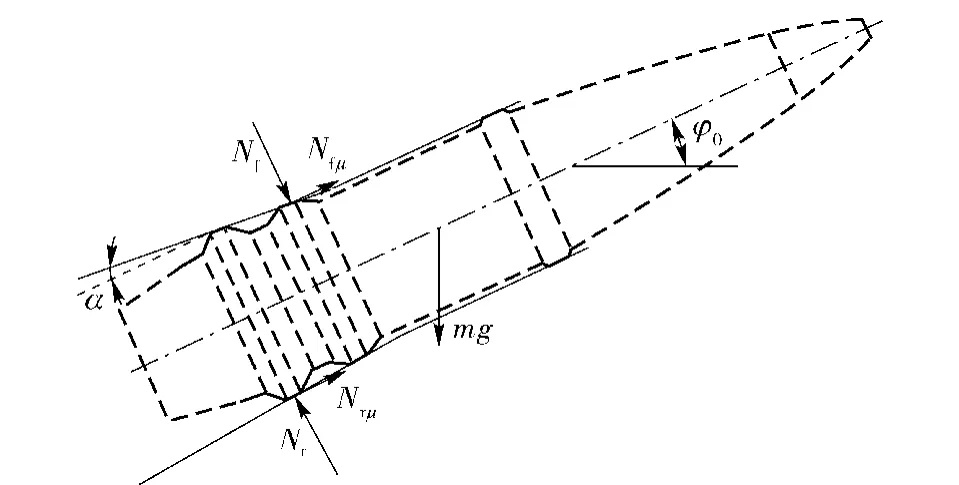
图4 弹丸卡膛力示意图Fig.4 Sketch of band-barrel reaction forces

某155 mm榴弹在仰角φ0=50°的身管上进行输弹,其卡膛速度u=3 m/s、弹带与身管间的动摩擦系数μd=0.2、正卡膛(Φ1=0°),以此进行弹丸卡膛过程弹带弹塑性仿真计算,得到了作用在弹带上沿坡膛法向作用力随时间的变化曲线,见图5.由图5可见,在卡膛过程中,前弹带先于后弹带约0.40 ms与坡膛发生接触碰撞,随后接触力迅速上升,且前弹带的接触力远远大于后弹带的接触力,在发生碰撞约1.4 ms后,前后弹带接触力开始趋于稳定,最终前弹带接触力Nf=4.63×105N,后弹带接触力Nr= 1.91×105N,根据(2)式计算得到的卡膛力F= 93 800 N.

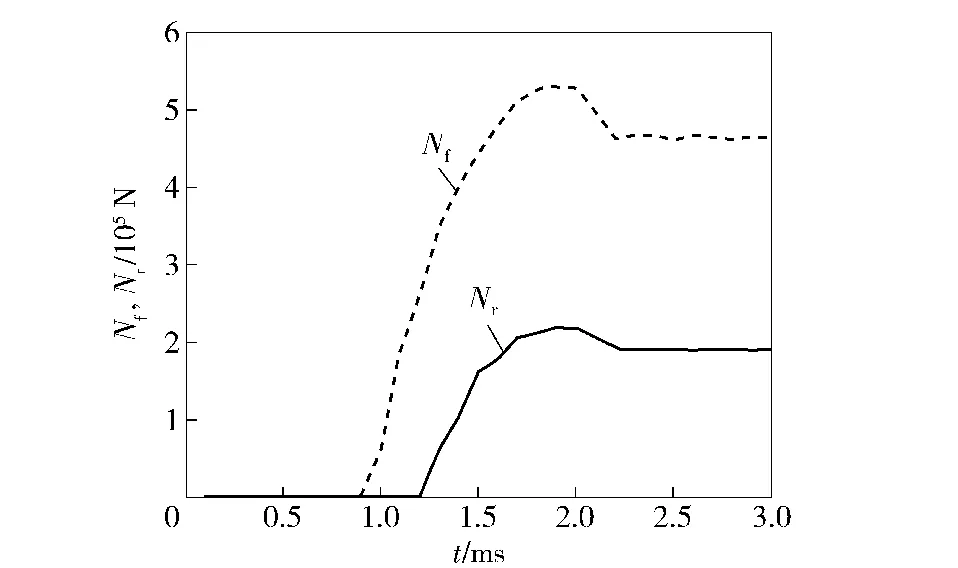
图5 弹带上坡膛法向力随时间变化规律Fig.5 Forces acting on the band in the normal direction of the forcing cone

2 正卡膛过程弹塑性分析

正卡膛是一种理想的状况,是指卡膛开始瞬间弹带与身管轴线同轴,即Φ1=0°的卡膛过程,也是相对简单的一种卡膛过程,对揭示弹丸卡膛过程中的各种物理现象具有重要的指示性意义。

2.1 卡膛速度的影响

若卡膛速度u过大,卡膛深度L会过深,导致药室容积增大,装填密度下降,初速降低,同时也会导致卡膛力F过大;若卡膛速度u过小,卡膛深度L会不足,卡膛力F过小不能保证稳定卡膛,弹丸可能会从坡膛滑落,击发点火后会使弹丸与身管产生强烈的冲击,导致身管内膛产生异常磨损和破坏。表2给出了在φ0=50°、μd=0.2、Φ1=0°的情况下,不同u与L、F、Φ2的关系。由表2可见:弹丸卡膛速度u与卡膛深度L之间存在线性关系,这可以理解为不同卡膛速度时应变率强化和温度软化效果基本一致,而卡膛力只是应变(位移)的函数;φ21随着卡膛速度u的增加而略有减小,φ22的量级很小,其原因可以这样来理解,高卡膛速度可以保证弹带在身管坡膛处快速对中,因而φ21减小;卡膛力F也随卡膛速度u的增加而增大,其原因是当卡膛过程的时间确定后,卡膛力与卡膛动量呈正比。由表2还可以看出,卡膛速度u散布导致卡膛深度L、卡膛力F的散布比摆角Φ2的散布大。

表2 不同卡膛速度u下的卡膛规律Tab.2 Laws of projectile band bayonet-chamber process with different projectile velocities

2.2 身管仰角的影响

以u=3 m/s,μd=0.2,Φ1=0°为计算条件,计算仰角φ0分别为0°、30°、50°、60°情况下卡膛结果L、Φ2、F的变化,计算结果见表3.由表3可见,在任意仰角条件下,只要卡膛速度u始终保持3 m/s的速度,重力对L、F基本无影响,对Φ2有一定影响,这是因为仰角越大,重力在身管径向方向上的分量mgcos φ0越大,卡膛力与重力之间形成的翻转力矩就越大。

2.3 摩擦系数的影响

随着射弹发数的增加,身管内壁受到高温高压火药气体的冲刷和弹丸的摩擦作用后,坡膛表面状态会发生变化[6],致使坡膛表面与弹带间的摩擦系数μd会发生变化。为此,以u=3 m/s,φ0=50°,Φ1=0°为计算条件,计算得到了当 μd分别为 0.30、0.25、0.20、0.15、0.10时弹丸的L、F、Φ2,结果见表4.结果显示,摩擦系数越大,卡膛深度越小,但卡膛力增大,稳定卡膛姿态角略有减小。

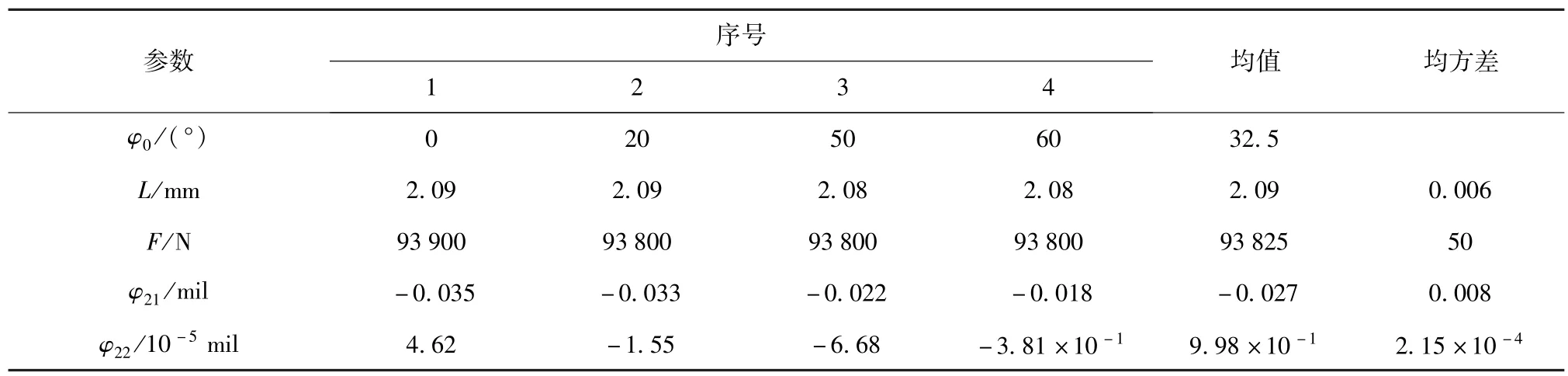
表3 不同身管仰角下的卡膛规律Tab.3 Laws of band bayonet-process with different quadrant angles

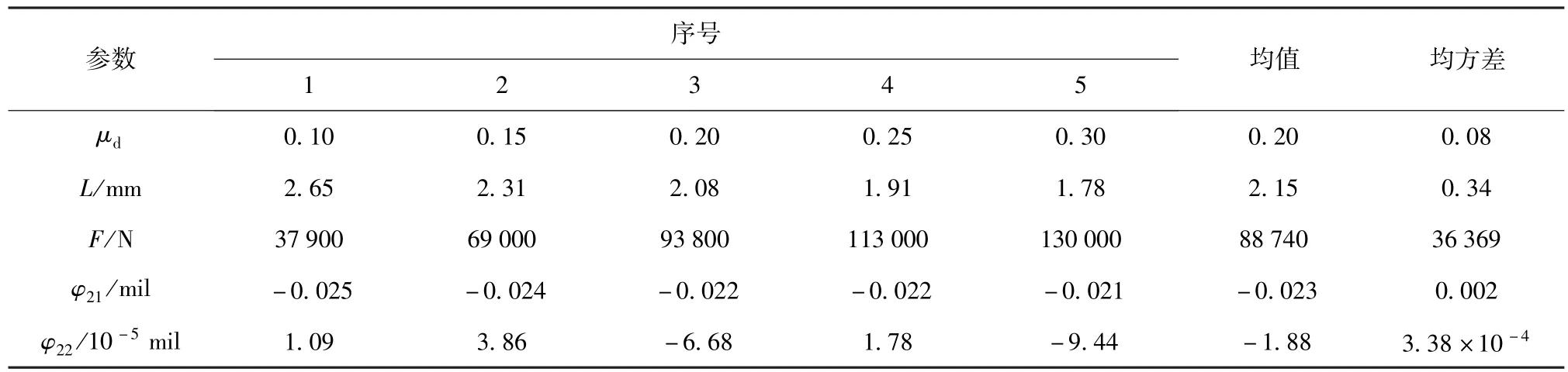
表4 不同摩擦系数下的卡膛规律Tab.4 Laws of projectile band bayonet-chamber process with different frictional coefficients

3 斜卡膛过程弹塑性分析

3.1 斜卡膛机理分析

由于不同因素的影响,弹丸的实际初始卡膛姿态处于非理想状态,即Φ1≠0°,此工况称为斜卡膛,导致斜卡膛的主要因素包括以下3项:

1)输弹过程中弹丸重力的作用;

2)输弹过程中弹丸与身管内膛的碰撞;

3)火药气体烧蚀导致弹炮间隙εg的变化。

在同一仰角φ0、卡膛速度u和摩擦系数μd条件下,影响L、F和Φ2的因素有εg、Φ1(φ11、φ12)等。这3个因素综合后对L、F和Φ2的影响可采用3因素5水平的均匀设计表U5(53)[7]来研究。计算时假定u=3 m/s、μd=0.2、φ0=50°,3个因素的选取范围:εg∈[0.05 mm,0.80 mm]、φ11∈[-2.0 mil, 2.0 mil],φ12∈[-2.0 mil,2.0 mil].

假定任一下界为p01、上界为p02的因素p,当j= 1,2,…,n时其插值pj为

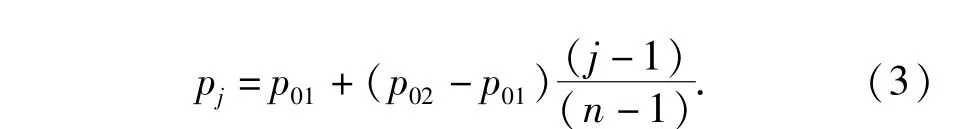
由此计算得到5个方案的卡膛结果,见表5.

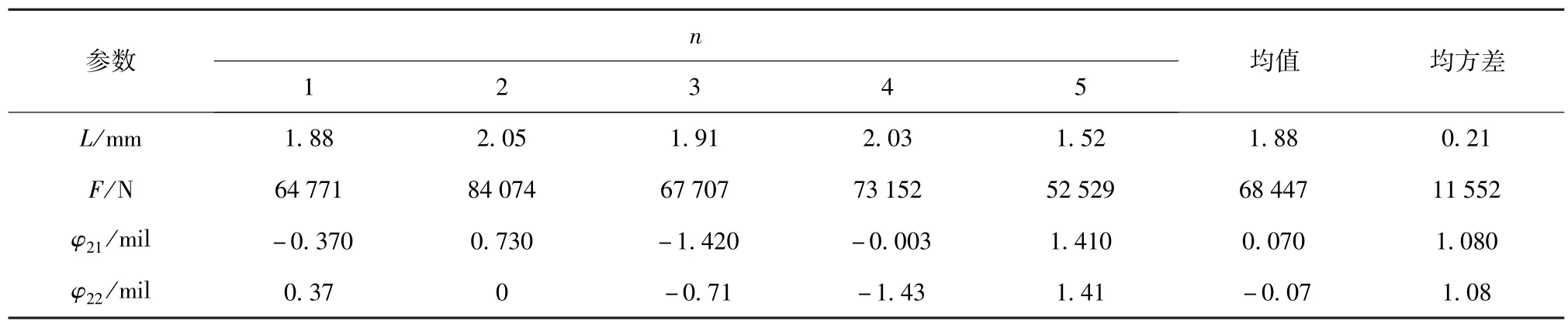
表5 不同卡膛姿态初始值对卡膛结果的影响Tab.5 Laws of band bayonet-process with some different initial values

由该表中的数据,可导出如下回归方程:

由表5及(4)式中给出的均值和方程数据还可以看出,弹炮间隙εg、初始卡膛姿态角Φ1散布导致卡膛深度L、卡膛力F、稳定卡膛姿态角Φ2的散布比较大。εg是影响L以及F的主要因素。

3.2 各因素综合的影响

通过前面的分析可以看出,在同一仰角φ0条件下,u、μd、εg、Φ1(φ11、φ12)共5个因素会影响L、F和Φ2.这5个因素综合后对L、F和Φ2的影响可采用5因素9水平的均匀设计表U9(95)来研究。

计算时假定φ0=50°,5个因素的选取范围为: u∈[2.0 m/s,3.5 m/s]、μd∈[0.1,0.3]、εg∈[0.05 mm,0.80 mm]、φ11∈[-2.0 mil,2.0 mil], φ12∈[-2.0 mil,2.0 mil].任意因素p的插值计算式pj采用(3)式。由此计算得到9个方案的卡膛结果,见表6.

表6 不同卡膛姿态初始值对卡膛结果的影响Tab.6 Laws of band bayonet-process with consideration to the changes in all the parameters

由该表中的数据,可导出如下回归方程:

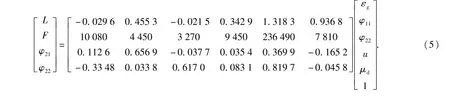
由(5)式中给出的均值和方程数据还可以看出,εg、Φ1、u、μd散布导致L、F以及Φ2的散布比较大,u是影响L和F的主要因素,而初始卡膛姿态角对稳定卡膛姿态角的影响是最显著的。另外,弹炮间隙对稳定卡膛姿态角也有较大影响。

4 结论

本文综合考虑不同的影响因素对卡膛结果的影响,得到了各个因素对卡膛结果的影响规律,具体结论如下:

1)弹丸卡膛过程中卡膛速度和摩擦系数对卡膛力和卡膛深度有较大的影响,卡膛速度的减小和摩擦系数的变大都会导致卡膛深度变小,身管仰角对卡膛深度的影响不大,但是对稳定卡膛姿态角有一定的影响。

2)弹炮间隙对3个卡膛结果均有较大影响,在身管使用过程中,随着身管内膛烧蚀磨损,该作用会逐渐体现,即随着身管使用,卡膛初始误差会增大。

3)初始卡膛姿态角对稳定卡膛姿态角有较大影响,在输弹过程中应该尽量减少磕碰,并合理安排输弹机位置以减少卡膛前弹丸与身管的碰撞。

4)经过计算得到了表征卡膛稳定性的卡膛力,但是究竟多大的卡膛力可以保证稳定卡膛仍有待进一步确定。

References)

[1] 赵森,钱勇.自行火炮半自动装填机构输弹问题研究[J].兵工学报,2005,26(5):592-594.

ZHAO Sen,QIAN Yong.Ammunition interior ballistics of atillery[J]. Acta Armamentarii,2005,26(5):592-594.(in Chinese)

[2] 李伟,马吉胜,孙河洋,等.弹丸惯性卡膛冲击问题动力学研究[J].振动与冲击,2011,30(5):161～163.

LI Wei,MA Ji-sheng,SUN He-yang,et al.Dynamic analysis for inertial bayonet-chamber process of a projectile[J].Journal of Vibration and Shock,2011,30(5):161-163.(in Chinese)

[3] 丁宏民,翟少波,杨晨晖.某大口径火炮装填过程弹带磕碰问题[J].火炮发射与控制学报,2007,12(4):17-19.

DING Hong-min,QU Shao-bo,YANG Chen-hui.Research on rotating band impact problem in the course of large caliber gun projectile loading[J].Journal of Gun Launch&Control,2007,12(4): 17-19.(in Chinese)

[4] 王宝元,衡刚,周发明,等.火炮测试技术进展[M].北京:国防工业出版社,2011:105-110.

WANG Bao-yuan,HENG Gang,ZHOU Fa-ming,et al.Progresses of measurement technology of gun[M].Beijing:National Defense Industry Press,2011:105-110.(in Chinese)

[5] 武丁二,王志兴,贺安之.采用二维PSD测量弹丸卡膛姿态的研究[J].华北工学院学报,1997,18(2):186-188.

WU Ding-er,WANG Zhi-xing,HE An-zhi.Study on measuring shell bayonet-chamber posture by plane PSD[J].Journal of North China Institute of Technology,1997,18(2):186-188.(in Chinese)

[6] 李怀学,陈光南,张坤,等.身管内膛复合镀铬层的组织退化特征[J].材料热处理学报,2007,28(4):111-115.

LI Huai-xue,CHEN Guang-nan,ZHANG Kun,et al.Degradation of microstructure of duplex electroplated chromium layers in gun barrels[J].Transactions of Materials and Heat Treatment,2007, 28(4):111-115.(in Chinese)

[7] 方开泰.均匀设计与均匀设计表[M].北京:科学出版社, 1994.

FANG Kai-tai.Uniform design and uniform design table[M]. Beijing:Science Press,1994.(in Chinese)

Analysis of Influence Factors of Projectile Band Bayonet-Chamber Process

LI Miao,QIAN Lin-fang,CHEN Long-miao,XU Ya-dong
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

The process of projectile band bayonet-chamber of a new type 155mm howitzer is analyzed to investigate the effect of band bayonet-process parameters on the initial conditions of motion of projectile in bore,and the effects of changes in various parameters of band bayonet-process are presented,such as projectile velocity,frictional coefficient,quadrant angle,initial deflection and barrel-projectile gap.The results are obtained based on the dynamic explicit finite element method.Thus,the factors that influence the bayonet-chamber depth,band-barrel reaction force and bayonet-chamber posture are shown.Among them,the projectile velocity and frictional coefficient have significant influence on the bayonet-chamber depth and the band-barrel reaction force,the quadrant angle and initial deflection have major impact on the bayonet-chamber posture,meanwhile,the barrel-projectile gap playes an important role in all the three results.The results provide a parameter basis to the ammunition rammer design and the motion law of projectile in bore.

ordnance science and technology;bayonet-chamber;finite element method;result of band bayonet-chamber process

TJ303

:A

:1000-1093(2014)08-1152-06

10.3969/j.issn.1000-1093.2014.08.003

2013-11-01

国家自然科学基金项目(51205207)

李淼(1988—),男,博士研究生。E-mail:limitmiao@163.com;钱林方(1961—),男,教授,博士生导师。E-mail:lfqian@vip.163.com