负三项分布的性质研究

王 慧，卓泽朋

（淮北师范大学 数学科学学院，安徽 淮北 235000）

概率论与数理统计是高等院校理工科各专业的一门专业基础课程，是研究随机现象统计规律性的数学学科，其蕴含的数学思想和方法已经广泛地渗透到计算机科学、经济、金融、生物、医学等多个领域.伯努利试验是一种非常重要的概率模型，它是“在同样条件下进行重复试验”的一种数学模型.历史上，伯努利概型是概率论中最早研究的模型之一，不仅在理论上具有重要意义，而且在实际生活中的应用也非常广泛.在一般的概率统计教材中均可见一些重要的基于伯努利试验的概率分布模型，如几何分布，二项分布，负二项分布等［1］.其中负二项分布又称巴斯卡分布，是近年来的研究热点之一，取得了丰富的研究成果：具体内容涉及负二项分布的统计性质及其应用［2-3］、数字特征［4-5］、概率的最大值点［6］、参数估计问题［7-8］、近似分布［9］等.文献［10］在负二项分布的基础上进行推广，提出负三项分布，并讨论负三项分布的概率分布和数字特征.但围绕负三项分布的研究还不够完善，本文将对其若干性质作进一步地探讨，首先从其特征函数出发，计算出其数字期望、方差及可加性，最后分析其概率的最大值点.

1 预备知识

文献［10］提出负三项分布的定义，并得出其概率分布.

定义1设在独立重复试验中，每次试验可能有3 种结果：A1,A2,A3，且P(Aj)=pj，j=1,2,3，p1+p2+p3=1，以Xj(j=1,2,3)表示Aj在独立重复试验中出现的次数，以X表示在独立重复试验中Aj出现rj(j=1,2)次时的试验次数，则称X服从负三项分布，记为X～NM(r1,r2;p1,p2).

设随机变量X～NM(r1,r2;p1,p2)，则X的可能取值为r1+r2，r1+r2+1，…，r1+r2+l，…，（rj≥1,j=1,2），其分布列为

下面给出特征函数的相关概念和性质［1］.

定义2设X是一个实值随机变量，其分布函数为F(x)，则称eitX的数学期望E(eitX)为随机变量X或其分布函数F(x)的特征函数，记为φX(x)或φ(x)，即

如果X是离散型随机变量，其分布列为

则

性质1如果随机变量X有n阶（原点）矩，则它的特征函数可微分n次，并且有

成立.

性质2如果随机变量X1,X2,…,Xm相互独立，则

2 负三项分布的性质

2.1 特征函数

引理1［10］设随机变量X服从负三项分布，即X～NM(r1,r2;p1,p2)，其中rj≥1，0＜pj＜1(j=1,2)，则

定理1设随机变量X服从负三项分布，即X～NM(r1,r2;p1,p2)，其中rj≥1，0＜pj＜1(j=1,2)，则X的特征函数为

证明已知负指数二项展开式

特征函数在概率论中是一个极其重要的分析工具，利用其定义和性质可以简化概率论中的许多定理证明过程，下面通过特征函数来研究负三项分布的数字特征和可加性.

2.2 数学期望

定理2设随机变量X服从负三项分布，即X～NM(r1,r2;p1,p2)，其中rj≥1，0＜pj＜1(j=1,2)，则X的数学期望为

证明记r1+r2=r0，p1+p2=p0，1-p0=q0，由（7）式得

2.3 方差

定理3设随机变量X服从负三项分布，即X～NM(r1,r2;p1,p2)，其中rj≥1，0＜pj＜1(j=1,2)，则X的方差为

证明先求φ″(t)，记号r0，p0，q0同上，则

即（9）式成立.

注将定理2和定理3的证明过程与文献［10］中的证明过程相比，结果表明，使用特征函数证明负三项分布的数学期望和方差，计算量大大减少，过程更加简洁.

2.4 可加性

所谓可加性，是指有限个相互独立的、服从统一分布的随机变量，其和也服从该分布，且该分布中的参数是相应参数之和.例如，二项分布、泊松分布、正态分布等均具有可加性［1］，本文接下来给出负三项分布在同参数p1,p2下也具有可加性.

引理2（唯一性定理）［1］分布函数F1(x)与F2(x)相等的充要条件是它们的特征函数φ1(x)与φ2(x)相等.

定理5设随机变量X1,X2,…,Xm相互独立，且均服从负三项分布，即X1～NM(s11,s21;p1,p2)，X2～NM(s12,s22;p1,p2)，…，Xm～NM(s1m,s2m;p1,p2)，其中shj≥1,h=1,2;j=1,…,m，则也服从负三项分布，即X～NM(r1,r2;p1,p2)，其中r1=s11+s12+…+s1m,r2=s21+s22+…+s2m.

证明用数学归纳法.

当m=2 时，若X1～NM(s11,s21;p1,p2)，X2～NM(s12,s22;p1,p2)，且相互独立，X=X1+X2，记p1+p2=p0，1-p0=q0，s11+s12=s01，s21+s22=s02，则，由（5）式得

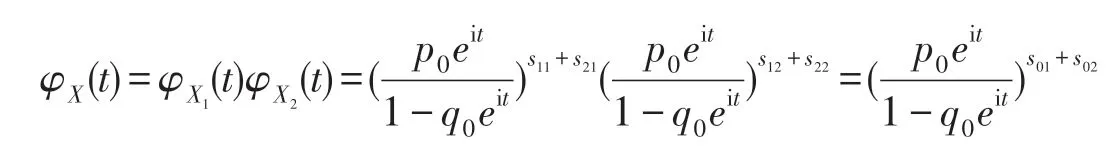
由引理2知，X～NM(s01,s02;p1,p2)，即X～NM(s11+s12,s21+s22;p1,p2).

假设m=k时成立，此时，Xj～NM(s1j,s2j;p1,p2)，j=1,2,…,k，则

且其特征函数为

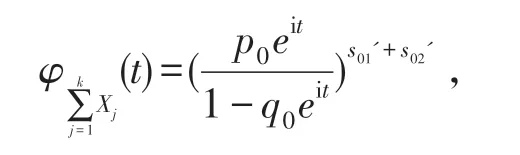
其中s11+s12+…+s1k=s01'，s21+s22+…+s2k=s02'.

当m=k+1时，独立，则

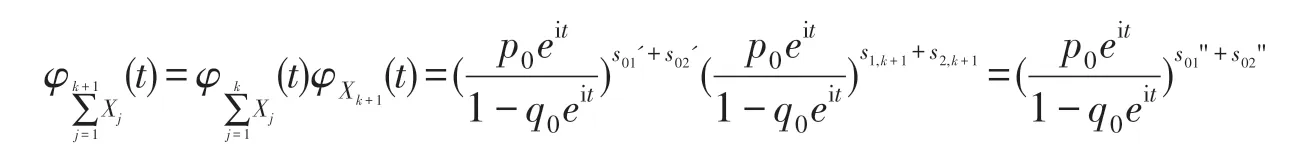
其中s11+s12+…+s1k+s1,k+1=s01"，s21+s22+…+s2k+s2,k+1=s02".即

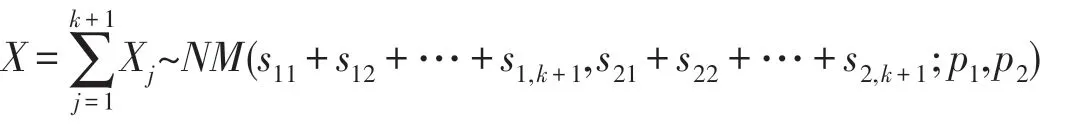
由归纳法证得，对一切正整数m，负三项分布具有可加性.

2.5 概率的最大值点

针对“负三项分布的概率何时取得最大值”这一问题进行分析，得到以下结论.

定理6负三项分布的概率分布如（1）式所示，则

证明由于

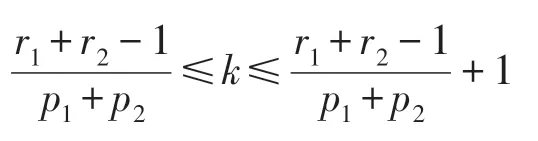
由于k∈Ζ+，因而当不是整数时时的概率取得最大，当为整数时，k在两处概率同时取得最大值.

3 结束语

伯努利试验是概率论中重要的随机试验，对基于伯努利试验的概率模型——负三项分布的理论研究是一项有意义的工作，本文主要讨论了负三项分布的特征函数、数学期望、方差、可加性等方面的性质，以特征函数为工具改进了文献［10］中的定理证明过程.同时，还给出了该分布的概率最大值点，为实际应用中使用负三项分布的概率最大值或最大值点时提供了方便.

［1］安徽师范大学数学系.概率论与数理统计［M］.上海：上海科学技术出版社，1988.

［2］孟生旺.负二项分布的优良特性及其在风险管理中的应用［J］.数理统计与管理，1998，17（2）：9-12.

［3］孙道德.负二项分布的性质及其应用［J］.阜阳师范学院学报：自然科学版，2000，17（2）：10-12.

［4］吴雪芹.负二项分布的数字特征及条件概率的封闭性的研究［J］.鄂州大学学报，2006，13（3）：56-57.

［5］韩非.计算二项分布与负二项分布期望与方差的新思路［J］.新乡学院学报：自然科学版，2008，25（2）：9-11.

［6］何春.负二项分布概率的最大值点［J］.生物数学学报，2011，26（1）：160-162.

［7］汤胜道，汪凤泉.负二项分布下参数的方差一致最小无偏估计及贝叶斯估计［J］.安庆师范学院学报：自然科学版，2003，9（1）：69-71.

［8］程维虎，王莉丽.负二项分布两种参数估计及其比较［J］.数理统计与管理，2004，23（5）：52-56.

［9］生志荣.负二项分布的两种近似分布及其比较［J］.统计与信息论坛，2011，26（1）：20-22.

［10］黄伟，刘瑞元.负三项分布［J］.高师理科学刊，2007，27（5）：16-19.