新的无证书的门限代理签名方案

马陵勇，廉玉忠

（东莞理工学院 城市学院计算机与信息科学系，广东 东莞 523106）

代理签名的概念首先是由Mambo等［1-2］提出的，在原始签名人与代理签名人之间形成的某种授权协议下，代理签名人可以行使原始签名人的签名权对文件进行有效签名.当代理签名的接收者验证一个代理签名时，需要同时验证签名和原始签名者的授权协议.代理签名的实用性较强，目前仍是数字签名领域研究的热点课题之一.

传统的代理签名大多是基于证书的公钥密码系统（PKI）［3］和基于身份的公钥密码系统（ID-PKC）.在基于证书的公钥密码系统中，由于需要验证用户公钥的真实性和有效性，使得基于证书的公钥密码系统的效率不高，为了克服这个缺点，Shamir［4］提出基于身份的公钥密码体制的概念.在该体制中，用户的公钥就是用户的身份信息，因此不必保存公钥证书列表，也不必使用在线的第三方.但是在这种体制中，用户的私钥完全由可信中心（PKG）产生，这就使得该签名体制不可避免地有一个致命的缺陷，就是密钥托管问题.基于这个问题，Al-Riyami和Paterson［5］于 2003年提出无证书的公钥密码系统，该系统同样要用到一个第三方KGC，与基于身份的密码系统不同，基于证书的密码系统中的 KGC 并不是生成用户的完整私钥，而只是生成用户的部分私钥，用户的完整私钥由用户和KGC通过一定合作产生，因此，无证书密码体制并不是简单的基于身份的密码体制.无证书密码体制一经提出就受到广泛关注，把无证书密码体制的概念加入到代理签名中可以提出非常有效的无证书代理签名方案［6-9］.

数字签名的安全性取决于签名所使用的密钥，门限技术可以将签名密钥以门限方式分散给多人管理，由此可以部分解决密钥管理中的密钥泄露和密钥遗失问题.将门限签名引入到代理签名制中，就形成门限代理签名，在一个（t，n）门限代理签名中，原始签名人给n个代理人进行授权，而在签名阶段，只有不少于t个人同意合作，才能生成有效的代理签名，这就实现了对代理签名权力的分配和对代理密钥的分散保管，提高了系统安全性，文献［10-11］分别提出一个高效安全的门限代理签名方案，但都是基于证书的.

本文在文献［9］中利用拉格朗日插值公式引入门限思想，提出一个新的高效安全的无证书门限代理签名方案.

1 预备知识

定义1双线性对

设G1是一个阶为素数q的加法循环群，P是它的一个生成元；G2是一个阶为q的乘法循环群.映射e:G1×G2→G2满足

（1）双线性性：对于任意U,V∈G1,a,b∈Z*q，e(aU,bV)=e(U,V)ab；

（2）非退化性：存在U,V∈G1，使得e(U,V)≠1G2；

（3）可计算性：对于任意的U,V∈G1，存在已给高效的算法来计算e(U,V)的值.

则称这个映射为双线性对.

定义2离散对数问题

给定一个阶为q的循环群G，它的一个生成元g以及h∈G，找到一个值

定义3计算Difiie-Hellman问题

给定一个阶为q的循环群G，它的一个生成元P以及aP,bP∈G且值未知），计算abP∈G.

2 新的无证书的门限代理签名方案

2.1 系统参数生成

设(G1,+)和(G2,·)均是阶为q的循环群，e:G1×G2→G2是双线性映射，H1,H2：是5个安全的密码学哈希函数.密钥生成中心（KGC）随机选择作为系统主密钥并保密，P是G1的一个生成元，系统公钥为PPub=tP，设g=e(P,P)，公开参数

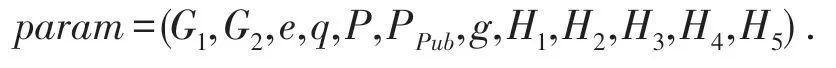
2.2 代理产生

设原始签名者的身份为ID0，秘密值x0,公钥P0,委托证书mw，部分私钥为D0,其中P0=x0P，Q0=H1(ID0‖P),D0=tQ0，私钥为S0=D0+x0T0=D0+x0H2(ID0‖P0).

代理产生阶段，原始签名者计算

（1）随机选择r0∈，计算y0=gr0；

（2）计算h0=H3(mw‖y0‖ID0‖P0)，K0=r0P-h0S0；

（3）签名w和mw,σw=(y0,K0)).

2.3 代理生成验证

代理群管理员DC（是由安全中心选择的可信赖的群组管理员）收到原始签名者的签名w=(mw,σw=(y0,K0))后验证签名的正确性

（1）计算：T0=H2(ID0‖P0)，Q0=H1(ID0‖P)；

（2）验证等式y0=e(K0,P)e(P0,h0T0)e(PPub,h0Q0)是否成立，若成立，则接收签名，否则拒绝.

2.4 代理私钥生成

设代理签名者为{B1,B2,…,Bn} ,Bi的身份为IDi，秘密值为xi，公钥为Pi，部分私钥Di，其中Pi=xiP，Qi=H1(IDi‖P)，Di=tQi，管理员DC计算

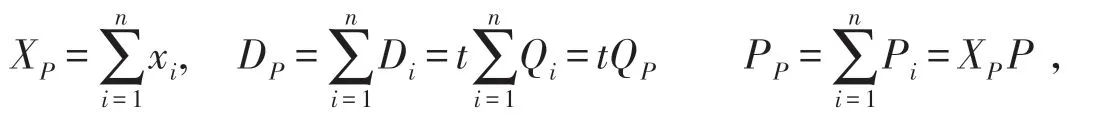
则代理私钥为KP=K0+DP+XPH1(ID0‖P).

2.5 代理分享阶段

群管理员DC随机选择(t-1)个数ai，构造安全多项式，计算yi=f(i)作为代理私钥，计算ui=e(IDi,yi)为代理公钥，并发送给代理签名者Bi，其中i=1,2,…,n.

2.6 代理签名阶段

设参与签名的代理者为t人，其中t≤n,对消息m进行代理签名，每个参与者各自计算KPi=yiLi，并发送给管理员DC.

DC计算

（2）随机选择rp∈,计算RP=rPP；

（3）计算hP=H4(m‖mw‖y0‖Rp‖u)，gP=H5(m‖mw‖y0‖RP‖PP)；

（4）计算VP=K0+gPDP+(rP+hPXP)QP；

（5）代理签名wP=(m,mw,δ=(y0,RP,VP)).

2.7 代理签名验证

收到代理签名者的签名后验证签名的正确性.

（1）消息m是否在委托证书mw的范围内，若不是，则拒绝签名；否则，执行（2）.

（2）计算Q0=H1(ID0‖P),T0=H2(ID0‖P0)

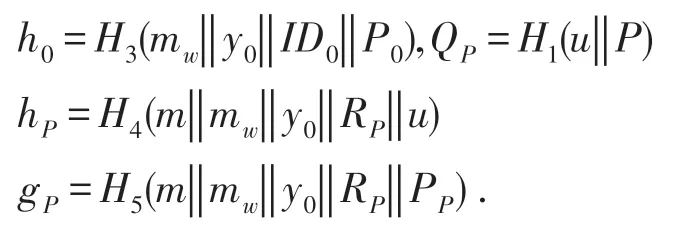
（3）验证等式

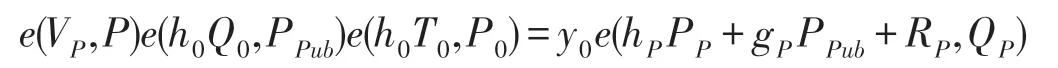
是否成立，当且仅当等式成立，则验证人接受签名；否则，拒绝签名.

3 正确性

3.1 代理生成的验证

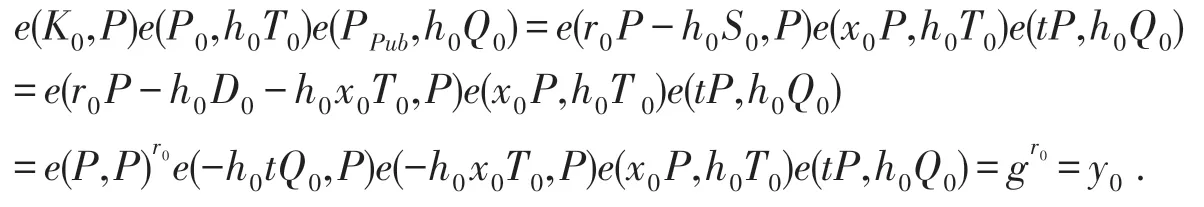
3.2 代理签名阶段的验证

因为

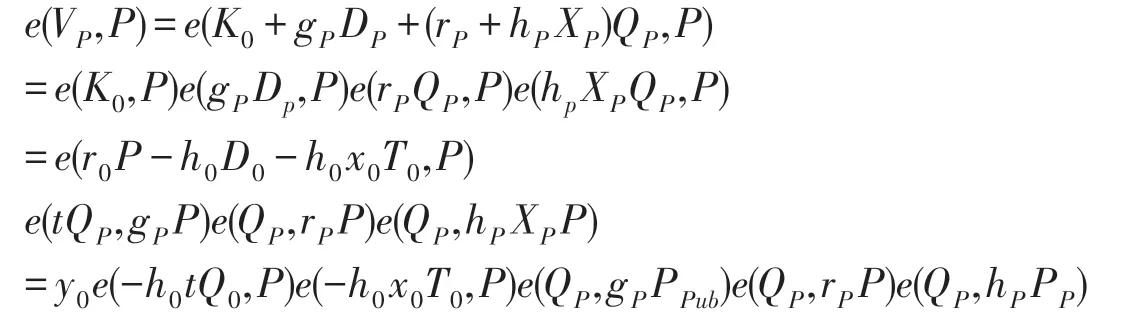
所以

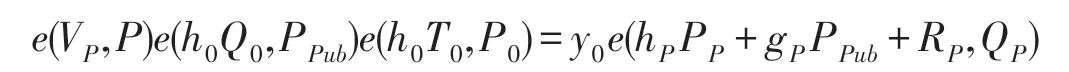
4 性能分析

（1）安全性：该门限代理签名方案的安全性可以由文献［9］证明，它是一个可证明安全的、不可抵赖的无证书门限签名方案.

（2）门限性：加入了门限思想，可由多个代理签名者共享代理密钥，仅需要t个成员就可以实现签名，这就解决代理签名者如部分成员脱机或有事不能参与时，签名无法顺利完成，增强方案的实用性和灵活性.

（3）高效性：该方案利用拉格朗日插值公式实现门限性的共享性，并没有降低方案的高效性，仍具有方案［9］的高效性.

5 结论

在文献［9］提出的无证书代理签名方案中引入门限思想，提出一个新的无证书门限代理签名方案，新方案具有门限性、安全性和高效性.在该方案中是通过拉格朗日插值公式实现门限方法的，如何把其他实现门限的方法和代理签名方案结合是今后需要研究的一个方向.

［1］MAMBO M，USUDA K，OKAMOO E.Proxy signature：delegation of the power to sign message［J］.IEICE Transactions on Fundamentals，1996，E79-A：1338-1354.

［2］MAMBO M，USUDA K，OKAMOO E.Proxy signature for delgating signing operation［C］//Proc of the 3rdACM Confer⁃ence on Computer and Communications Security.ACM Press，1996.

［3］KIM S J，PARK S J，WON D H.Proxy signatures［C］//Revisited.ICICS’97，LNCS1334［S.L.］：Springer-Verlag，1997：223-232.

［4］SHAMIR A.Identity based cryptosystems and signature schemes［C］//BLAKELY G R，CHAUM D.Proceedings of Cryp⁃to 1984，California，USA，1984，196：47-53.

［5］AL-RIYAMI S，PATERSON K.Certificateless public key cryptography［C］//LAIH C S.Proceedings of the Asiacrypt 2003，Taipei，Taiwan，2003，2894：312-323.

［6］LI X，CHEN K，SUN L.Certificateless signature and proxy signature schemes from bilinear pairings［J］.Lithuanian Mathematical Journal，2005，45：76-83.

［7］CHOI K，LEE D.Certificateless proxy signature schemes［C］//Proceedings of the 3rdInternational Conference on Multi⁃media，Information Technology and its Applications-MITA2007，Manila，Philippines，2007：437-440.

［8］杜红珍，温巧燕，李文敏，等.高效的无证书强代理签名方案［J］.北京邮电大学学报，2008，31（6）：18-21.

［9］宋万干，陈虎，张福泰.新的无证书代理签名方案［J］.计算机工程与应用，2011，47（4）：97-101.

［10］LEE N Y.Treshold proxy signature［J］.IEEE Trans，on Computer and Digital Techniques，1999，146（5）：259-263.

［11］ZHANG K.Threshold proxy signature schemes［C］//Information Security Workshop，Japan,1997：191-197.