CRH3动车组轮缘润滑系统可靠性分析
谈立成,李永华,高磊,田雪艳,兆文忠
(1.中国北车集团 唐山轨道客车有限责任公司 产品技术研究中心,河北 唐山063035;2.大连交通大学 交通运输工程学院,辽宁 大连 116028)*
0 引言
随着机车速度的不断加大,改善轮轨之间的润滑性能,对提高动车组的功率运用具有重要意义.所以CRH3动车组转向架采用轮缘润滑系统,改善了轮轨之间的润滑性能.轮缘润滑系统用于头车的第一个动力轮对上,该系统的作用是防止车轮轮缘贴靠钢轨时引起的轮轨磨耗[1].
轮缘润滑系统的可靠性是指该系统在规定的条件下,规定的时间内,安全、可靠地完成润滑的能力.为了有效地延长轮缘修磨的间隔时间,大幅提高轨道的使用寿命,减少列车脱轨的危险,有必要进行CRH3动车组轮缘润滑系统可靠性分析.
常见的系统可靠性分析方法主要有解析法、Monte Carlo法、Bayesian 法和混合法四种[2],其中解析法主要有网络图法、FTA法、FMEA法、状态空间法和GO法.网络图法主要应用于两状态元件组成的系统,不能模拟共因失效等多状态元件系统[3-4].FTA法是一种倒树状的逻辑因果关系图,其缺点是复杂产品的定量分析难度很大[5].FMEA是一种归纳性的方法,是系统地分析产品各组成单元所有可能的故障模式、故障原因及后果,以便发现设计中潜在的薄弱环节,提出可能采取的预防改进措施,以提高产品可靠性的一种设计分析方法.它常有相对固定的表格格式,只能进行定性分析[6].状态空间法以马尔可夫模型为数学理论基础,在元件的故障率和修复率都是常数的情况下可以求解得到系统状态的概率等指标.但当系统较为复杂时其状态空间图的结构会非常复杂,不太实用[3].而GO法是一种以成功为导向的系统概率分析技术[7-10],通过部件的GO操作码直接把原理图翻译成GO模型图,并用GO法程序计算所分析系统各种状态的发生概率,进而计算系统的可靠度.对于有多状态、有时序系统的可靠性和安全性分析更为合适[8].
有关GO法在动车组轮缘润滑系统可靠性分析中的应用研究相对较少,本文结合CRH3动车组轮缘润滑系统的工作原理,基于GO法的运算规则及GO法状态概率公式,按照GO法的具体分析步骤,采用信号流和操作符建立GO图模型,并进行精确的定量分析.
1 轮缘润滑系统工作原理
轮缘润滑系统的组成结构如图1所示.在单向运行的车辆上,轮缘润滑系统[1]包括:油箱、气动泵、油气混合块、电磁阀、Turbolub油气分配器、喷嘴、电控箱、管路和润滑剂等.其工作原理[1]是:通过一个气动柱塞泵将润滑剂打入油气混合块中,同时润滑剂和压缩空气在油气混合块中混合.借助于压缩空气的作用,润滑剂沿着管道内壁输送并经TURBOLUB分配器分配后送到喷嘴、喷射到轮缘上.
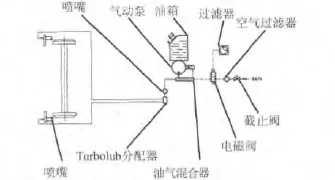
图1 轮缘润滑系统的组成结构图
2 建立轮缘润滑系统GO图模型
基于GO法的系统可靠性分析和运算以成功为准则[7].对于轮缘润滑系统,其成功准则就是轮缘润滑时各元件工作正常,保证润滑剂喷射到轮缘上.根据轮缘润滑系统的结构原理建立轮缘润滑系统的GO图模型,如图2所示.
由轮缘润滑系统的工作过程,确定系统的范围从压缩空气和油箱开始,直到润滑剂喷射到轮缘上.首先按照组成元部件的功能选择对应类型的操作符来代表各个元部件.系统的初始输入为压缩空气和油箱,以及电磁阀和气动泵的控制信号,因此用类型5输入操作符来表示这些输入;电磁阀和气动泵不仅需要主信号,还需要控制信号才能导通,因此用类型6有条件信号而导通的操作符代表;润滑剂和压缩空气要在油气混合块中混合,两者都导通才能实现在油气混合块中混合,因此用类型10与门的操作符表示;其他部件如空气过滤器、油气混合块、过滤器、Turbolub油气分配器、喷嘴等都是有成功和故障两状态,用类型1两状态单元操作符代表.操作符按照GO法的建模规则确定后,即可由系统图直接生成轮缘润滑系统的GO图.
轮缘润滑系统是一个简单的两状态系统,各部件只有成功和故障两个状态,没有提前状态,信号流也只有成功和故障两个状态,用状态值1和2表示.轮缘润滑系统有4个输入操作符,8个功能操作符和一个与门操作符,其成功和故障状态概率数据列于表1.

图2 轮缘润滑系统GO图
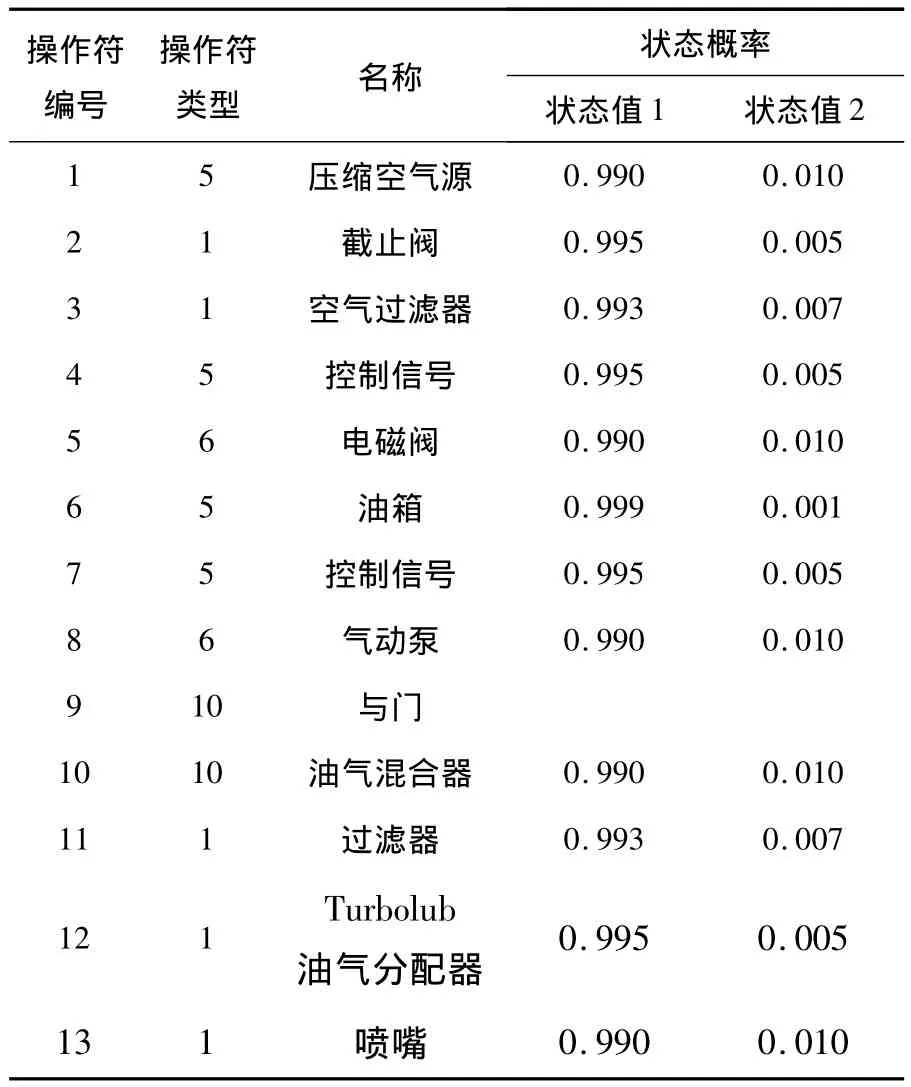
表1 轮缘润滑系统操作符数据
3 轮缘润滑系统GO法定量分析
轮缘润滑系统GO图模型是简单的两状态系统,故N=2,没有提前状态.因此信号流的状态概率P(0)=0.0,P(1)为成功状态概率,P(2)为故障状态概率.信号流的状态累积概率为:
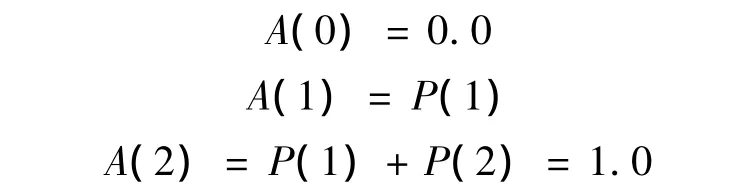
轮缘润滑系统中,输入信号操作符1、4、6和7的状态概率直接由输入操作符数据给出,然后按照GO图中信号流序列,对操作符逐个进行定量计算即得到所有信号流的状态概率.
轮缘润滑系统的定量计算过程如下:
(1)输入操作符定量计算,输入操作符1、4、6和7的输出信号状态概率就等于操作符的状态概率,因此直接可得到信号1、4、6和7的状态概率,见表2.
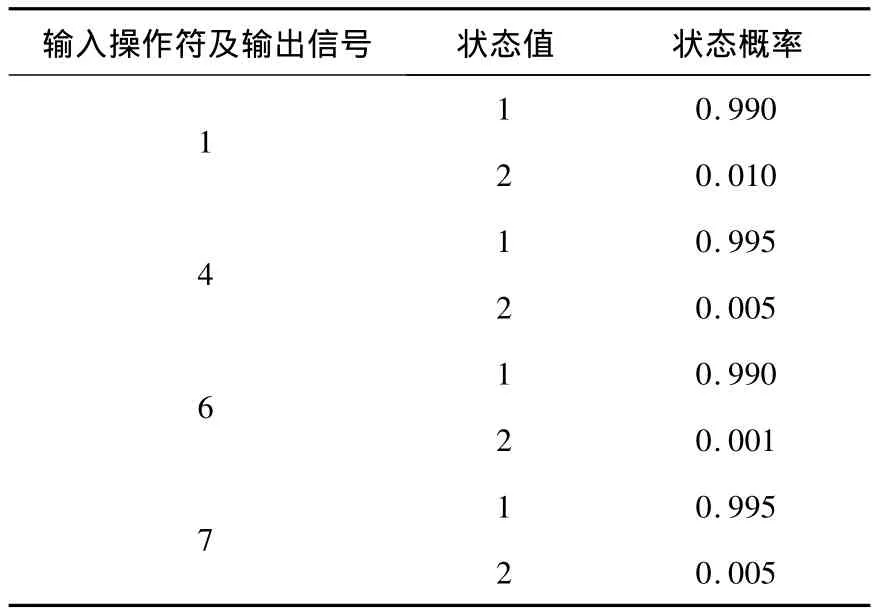
表2 输入操作符1、4、6和7的状态概率计算
(2)操作符2是类型1操作符,由其输入信号和操作符2的状态概率直接计算输出信号2的状态概率,计算表达式为:
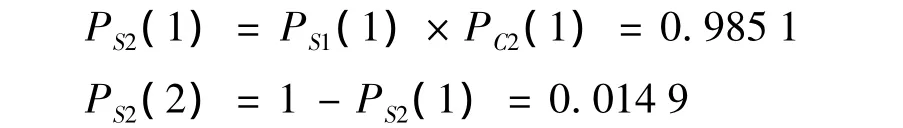
计算结果列于表3.
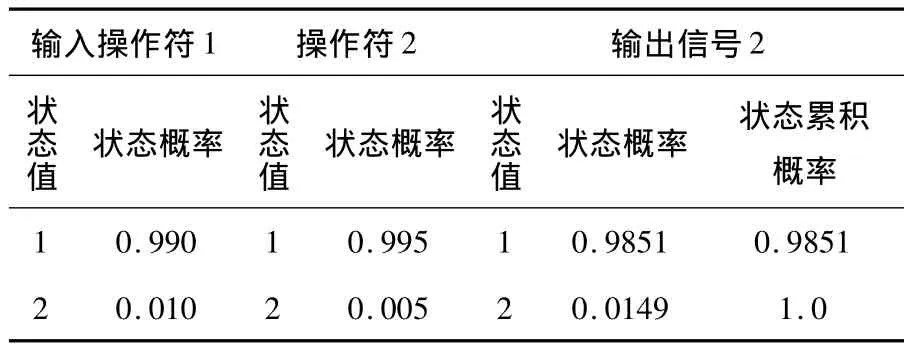
表3 操作符2的状态概率计算
(3)操作符3和操作符2,其输出信号3的状态概率计算结果列于表4,计算表达式为:
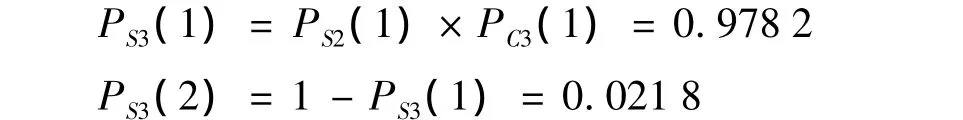
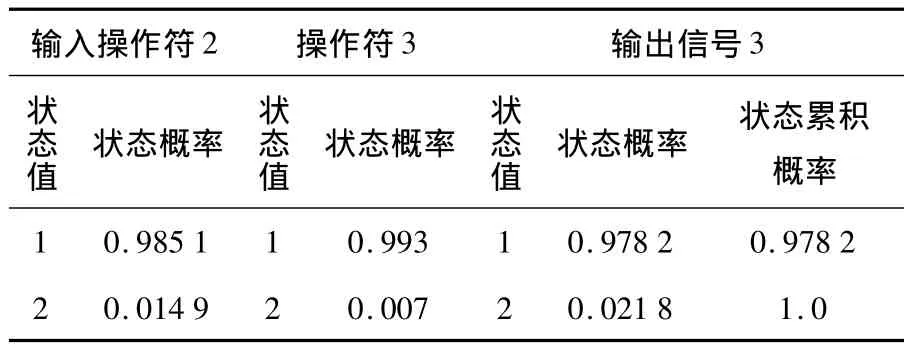
表4 操作符3的状态概率计算
(4)操作符5是类型6操作符,主输入信号3,次输入信号4,由类型6操作符状态累积概率公式计算,计算表达式为:
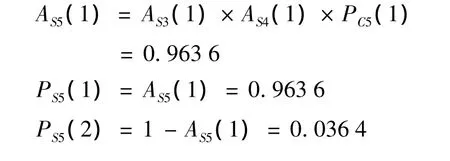
计算结果列于表5.
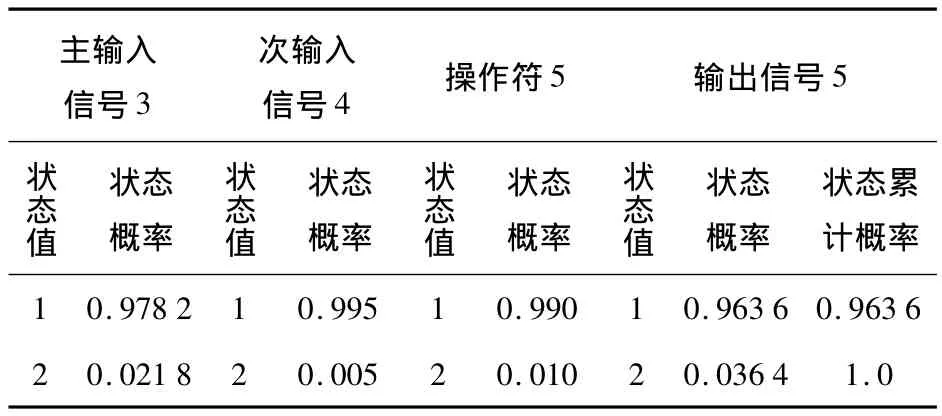
表5 操作符5的状态概率计算
(5)操作符8和操作符5,其输出信号8的状态概率计算结果列于表6,计算表达式为:
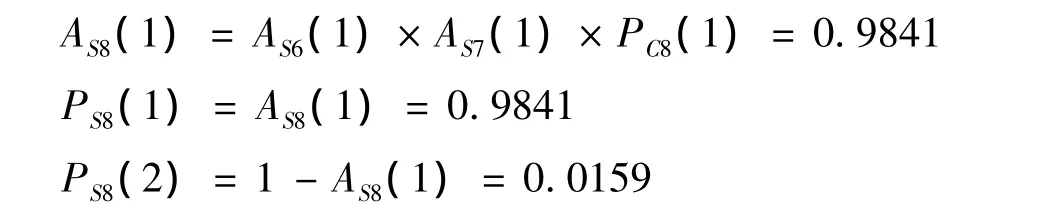
计算结果列于表6.
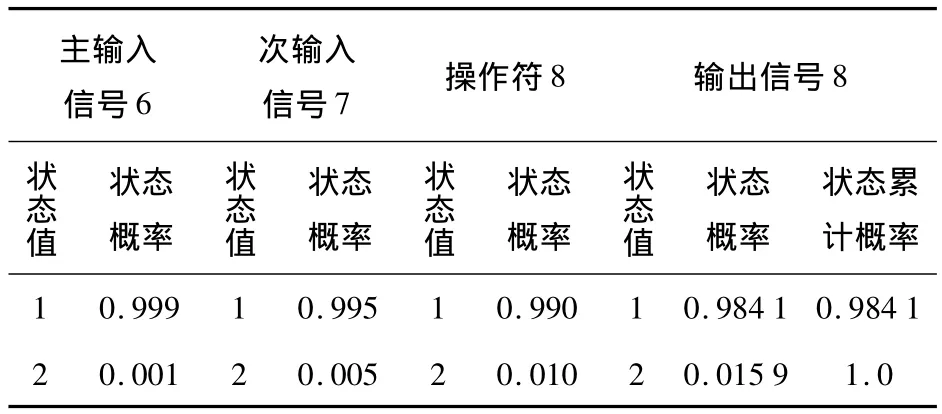
表6 操作符8的状态概率计算
(6)操作符9的状态概率计算,操作符9是类型10与门操作符,按与门的概率计算公式,得到输出信号9的状态概率,计算表达式为:

计算结果列于表7.
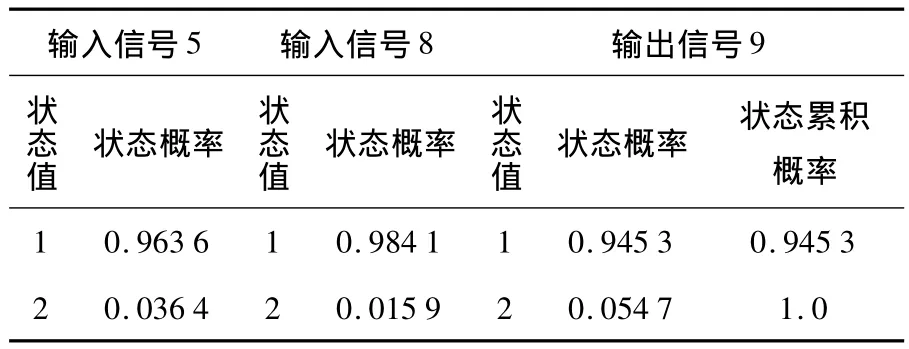
表7 操作符9的状态概率计算
(7)操作符10和操作符2,其输出信号10的状态概率计算结果列于表8,计算表达式为:
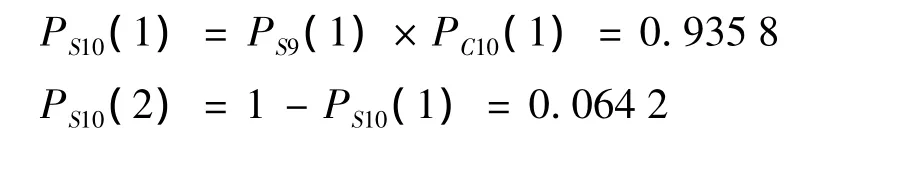
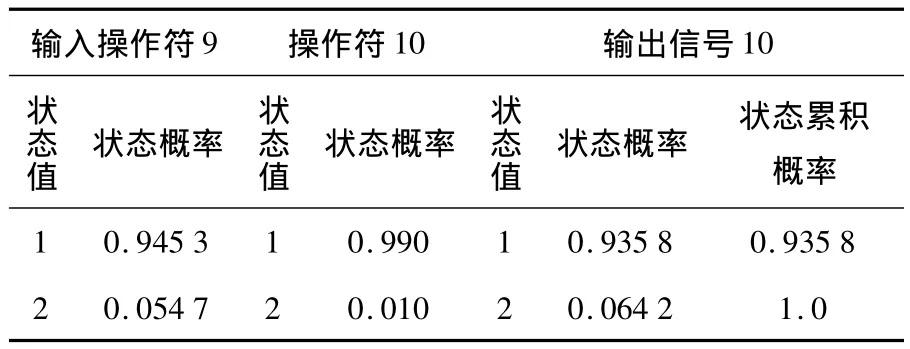
表8 操作符10的状态概率计算
(8)操作符11和操作符2,其输出信号11的状态概率计算结果列于表9,计算表达式为:
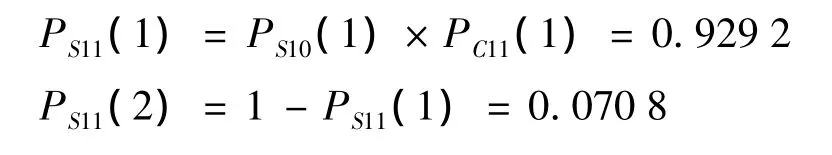
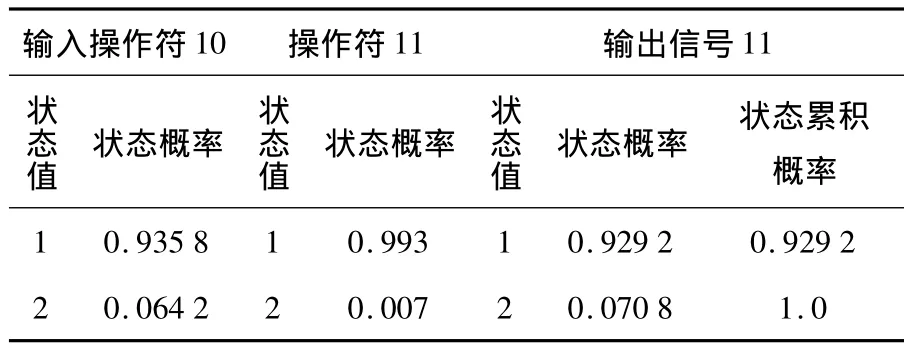
表9 操作符11的状态概率计算
(9)操作符12和操作符2,其输出信号12的状态概率计算结果列于表10,计算表达式为:


表10 操作符12的状态概率计算
(10)操作符13和操作符2,其输出信号13的状态概率计算结果列于表11,计算表达式为:
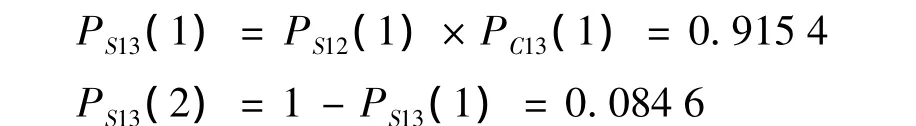
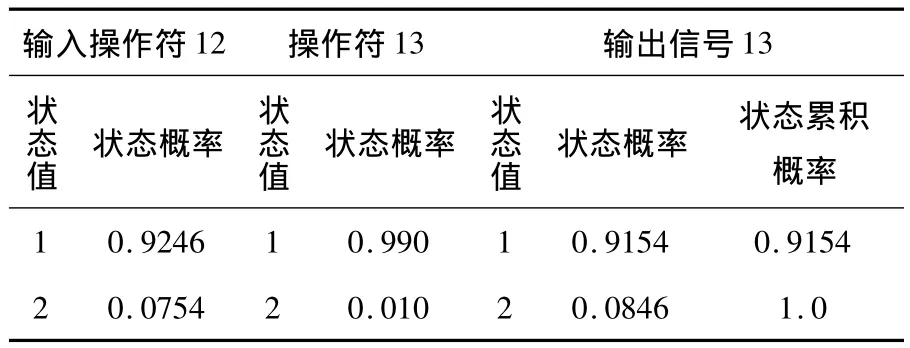
表11 操作符13的状态概率计算
综上所述,得到系统全部信号流的状态概率P和状态累计概率A,见表12.

表12 系统信号流状态概率和状态累计概率表
输出信号13代表系统,故系统的状态概率如表13.

表13 系统状态概率
由表13可以看出,轮缘润滑系统正常工作的概率为0.9154,其可靠性不高,有必要采取措施提高其可靠性水平.利用GO法得到的运算结果和采用FTA法得到的系统正常工作的可靠度值也基本相同,但与故障树分析法相比GO法可以减少工作量和降低建模差错.
4 结论
基于CRH3动车组轮缘润滑系统模型,将GO法引进到轨道设备领域.本文对CRH3动车组轮缘润滑系统建立对应的GO图,采用状态概率公式算法,进行了定量分析计算,得到了该系统的状态概率,对CRH3动车组轮缘润滑系统的可靠性分析和评价提供了科学的量化根据,进而论证了利用GO法分析轮缘润滑系统可靠性是可行的.
由以上分析可知,GO法能够较好的体现系统功能关系,操作符与元件几乎是一一对应,GO法的操作码和信号流可以准确地表示系统的多个状态,以及模拟有序列过程的状态系统.GO法思路清晰明了,易于理解.较好地解决了传统可靠性分析方法模型的复杂性、计算量大等问题,因此更适用于规模较大得系统可靠性分析计算.
采用GO法对CRH3动车组轮缘润滑系统进行可靠性分析是实际可行.在轨道列车系统设备可靠性分析中,发展GO法的应用有着十分重要的现实意义.
[1]张曙光.CRH3型动车组[M].北京:中国铁道出版社,2007.
[2]曹景雷.基于GO法的地铁牵引供电系统可靠性研究[D].成都:西南交通大学,2012.
[3]游专,何仁.基于GO法的汽车EPS系统可靠性分析[J].实验室研究与探索,2013,32(1):220-224.
[4]NABIL S,HAMID D.Reliability analysis of discrete event dynamic systems with Petri nets[J].Reliability Engineering and System Safety,2009,9(11):1848-1861.
[5]BERESH R,CIUFO J,ANDERS G.Basic fault tree analysis for use in protection reliability[J].International Journal of Reliability and Safety,2008,2(1-2):64-78.
[6]ARABIAN H,ORAEEA H,TAVNERB P J.Failure Modes and Effects Analysis(FMEA)for wind turbines[J].International Journal of Electrical Power& Energy Systems,2010,32(7):817-824.
[7]沈祖培,高佳.GO法原理和改进的定量分析方法[J].清华大学学报(自然科学版),1999,39(6):15-19.
[8]沈祖培,黄样瑞.GO法原理及应用[M].北京:淸华大学出版社,2004.
[9]MATSUOKA T,KOBAYASHI M.The GO-FLOW reliability analysis methodology-analysis of common cause failures with uncertainty[J].Nuclear Engineering and Design,1997,175(3):205-214.
[10]高振清,孙厚芳,吴琼.基于GO法的制造系统可靠性分析[J].机械科学与技术,2007,26(3):320-323.

