城市轨道交通站间距优化研究

左忠义，赵汉鲲

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

0 引言

随着我国现代化、城市化步伐的深入，城市交通问题突显.城市轨道交通系统作为一种能够有效改善城市交通拥挤现状的公共交通运输方式，它的运行是否更加高效、快捷，是否能够充分发挥城市轨道交通系统在改善城市交通状况中的作用，现在正受到越来越多的关注.而站间距作为影响轨道交通工程建设和运营效率的一个重要指标，也逐步显现出了它的重要性.目前国内在城市轨道站间距优化方面已经有了不少的成果:王芳在考虑了城市轨道交通与常规公交相协调的情况下，根据出行时间对站间距进行了优化［1］;姚新虎在比较了城市轨道交通与常规公交的出行耗时随出行距离的变化关系后，依据出行时间构建了模型对站间距进行了优化［2］;王怡璇在总出行时间与站间距的关系模型的基础上求解分析了模型中各参数对站间距的影响，最终根据平均运行速度的变化程度来判断最优站间距［3］;李鹏提出了从出行时间、车票收入、工程运营费用等方面建立站间距优化模型，但并未给出数据进行实际测算分析，没能得到实际结论［4］;左大杰、王慈光以轨道交通乘客总出行时间最少为目标建立了总出行时间与站间距的函数关系模型，并进行了计算［5］;魏金丽等人分析了城市轨道站间距设定的诸多影响因素，最终根据乘客出行时间和列车运行的实际参数指标对站间距进行了优化［6］.从目前城市轨道交通站间距优化方面的研究成果来看，很多研究仍以或者说最终仍回到乘客出行时间的计算上并没有实际引入其他经济影响因素，而仅仅是根据停战时间、车辆最高行驶速度、车辆加速度等相关参数对站间距的变化进行限定，最终确定最优平均站间距.而本文希望从真正意义上引入其他经济指标连同出行时间建立模型，并根据实际数据做出计算得到结论.因此，在本文中引入了车票收入，并将乘客出行时间量化为与车票收入同样的经济指标来建立城市轨道效益模型，并根据实际数据实施计算，得到优化后的平均站间距.

1 站间距相关影响因素分析

1.1 客流分布特征

客流分布对站间距优化模型的建立有着重要影响.首先我们需要获得近期轨道交通预测客流:通过分析所涉及区域的人口、就业及土地使用情况的变化，依此进行出行产生量预测;然后根据居民出行调查建立居民出行分布模型，预测近期居民全方式出行OD，在此基础上进行交通方式划分，得到公共交通近期预测OD，最终结合现有公共交通客流集散点，在公交网上进行常规公交和轨道交通的客流分配，最终得到轨道交通近期OD客流预测.

在轨道交通近期客流预测的基础上，我们根据轨道交通线路总长度，假定各交通客流集散点之间距离是相等的，通过对预测数据的分析整理，近似得到近期预测客流随居民乘轨道交通出行距离分布关系.根据某市地铁客流预测 OD［7］分析得到的该市地铁客流随出行距离的近似分布，之后对其进行拟合，最终得到图1为地铁客流随乘客出行距离的分布关系，以及客流与出行距离变化方程:

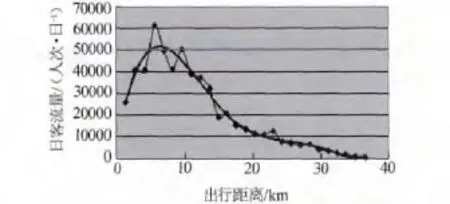
图1 地铁客流随出行距离变化图

客流随距离变化方程:

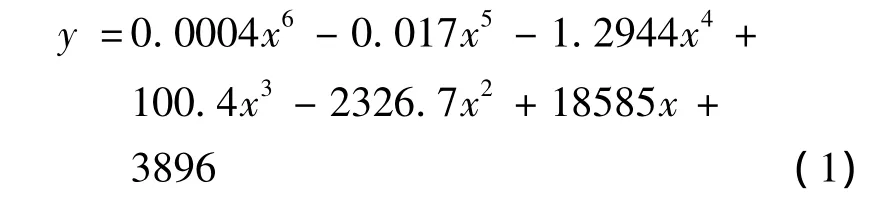
式中，y为地铁某一出行距离的近期预测全日客流量(人次 /日);x为乘客乘地铁出行距离(km).

1.2 乘客出行时间

乘客出行时间包括:乘客到离轨道站点时间、列车中间停站时间、列车加速急减速运行时间、列车稳定高速运行时间.

(1)乘客到离轨道交通站点时间

乘客到达或离开轨道交通站点时，必然会存在一定的步行时间，实际生活中，一般情况下不论是从家直接步行至轨道交通车站，亦或乘坐出租车、小汽车以及常规公交转乘轨道交通的乘客，在到达或离开轨道车站时都会采用步行的方式(也有可能采用自行车方式，但从我国实际情况考虑，最终都假定采取步行方式).而这一步行方式的走行距离的限定，其应该小于常规公交的平均站间距，因为与轨道交通换乘的其他交通方式中，乘客出行距离与费用性价比最高的即为常规公交，因此若步行走行距离超过一个常规公交站间距，乘客会选择乘坐常规公交而并非步行.因此这段步行距离应小于常规公交平均站间距，约为450 m.式(1)为乘客到离轨道站点总时间的计算公式:

式中，t0为乘客到离轨道站点总时间(s);s0为乘客到站和离站走行距离之和(m);v0为乘客到站离站平均速度(m/s).

(2)列车停站时间:

首先，停站时间必须满足乘客上下车的时间需求;其次，停站时间的降低会提高轨道交通的运行效率，减少乘客的出行时间.结合各地轨道交通的中间停站时间分析，本文中停站时间t1取30 s为宜.

(3)列车加速及减速运行时间:

即列车的启动加速过程中以及制动减速过程中所用的时间，其计算公式如下:

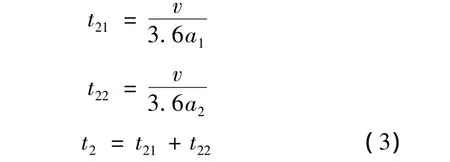
式中，t2为列车加速和减速运行时间和(s);t21为列车加速运行时间(s);t22为列车减速运行时间(s);v为列车稳定运行速度(km/h);a1为列车启动加速度(m/s2);a2为列车制动加速度(m/s2).

(4)列车稳定高速运行时间:

列车稳定高速运行时间指列车启动加速到平稳运行速度后一直到到达下一车站制动加速之前，在平稳匀速状态下的运行时间.计算公式如下:

式中，d为平均站间距(km);t3为列车稳定高速运行时间(s).

假设乘客到达车站时完整经历了起始站的停站时间，最终得到乘客出行时间的公式:

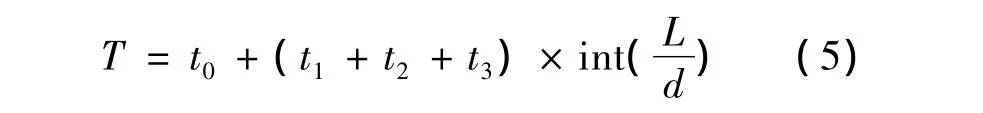
式中，T为乘客出行总时间(s);L为线路总长度(km).

2 站间距优化模型的建立和计算

2.1 车票收入的计算

(1)车票收费标准:

经过对国内外多地轨道交通车票收费标准分析，得到轨道交通收费标准大致分为:单一票价制、计程票价制、区段票价制以及分区票价制四种方式见表 1［7］.

表1 轨道交通收费标准分类

某市的地铁收费按计程票价制收费的标准，如图2.

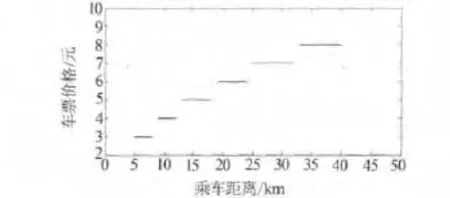
图2 某市地铁收费标准

继而根据表1得到某市地铁票价方程为:

式中，f(x)为为该市地铁票价(元);x为乘客乘坐地铁出行距离(km).

同时，发现乘客乘坐地铁出行的最小距离应该为一个站间距(d)，同时某市该段地铁线路总长为36.5 km.则近期预测全日车票收入计算公式如下:

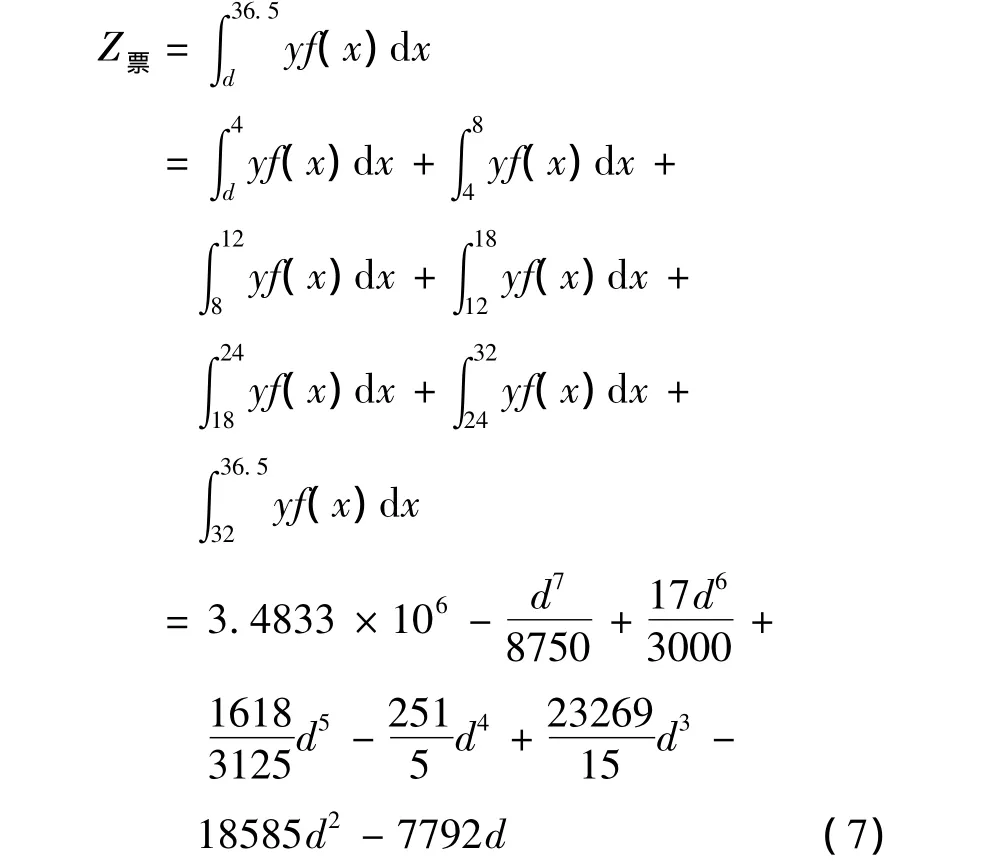
同时，本文用matlab软件以d取0.5～4，以0.1为间隔对车票收入方程进行取点计算，并绘图，得到图3为车票收入随站间距的变化曲线.

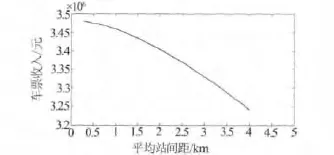
图3 车票收入随站间距的变化

2.2 乘客出行时间成本费用

在这一部分里将之前所分析的乘客出行时间转换成等值的经济效益，之后才能使其与其他因素之间进行定量计算.首先，从出行量上这里把工作和学习作为产生经济效益的即有产值的活动，而通过相关文献的查阅分析，可以得到出行中因工作和学习出行所占的的比率约为50%.而从出行时间上，人们将他们可支配的时间的30%用于工作和学习［10］.由此得到近期预测全日乘客出行时间成本转化的经济成本值的计算公式为:

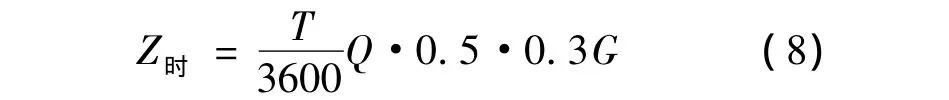
式中，Z时为期预测全日乘客出行时间成本转化的经济成本值(元);Q为某市地铁近期全日总客流预测值(人次);G为单位时间人均国民生产总值(元).某市的具体情况如表2.

表2 某市地铁具体参数

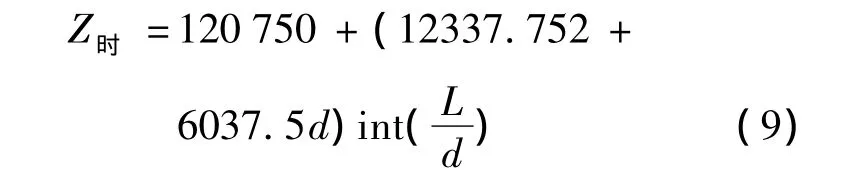
用matlab取d从0.3～4 km区间精度为0.1 km，对Z时进行计算并绘图，得到了图4.

根据表2中的数据求的Z时关于d的变化关系:

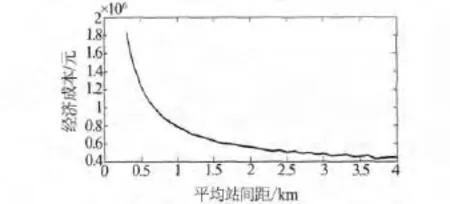
图4 乘客出行时间的经济成本随站间距的变化

2.3 建立站间距优化模型

确定d的取值范围，为了防止和常规公交发生冲突，同时提高城市公共交通整体利用率，减少交通资源的浪费，轨道交通平均站间距应大于常规公交平均站间距，而常规公交的站间距为300～500之间，而根据某市的实际数据v=40 km/h，a1=0.83 m/s2，a2=1 m/s2，站间距还应该满足列车的平稳高速运行距离大于列车加减速过程中所行距离的总和，由此算的站间距应大于270 m.而由该市的票价制定指标，再结合地区地铁站间距的经验，我们认为，平均站间距不应大于4 km.

因此得到总效益最大站间距优化模型为:

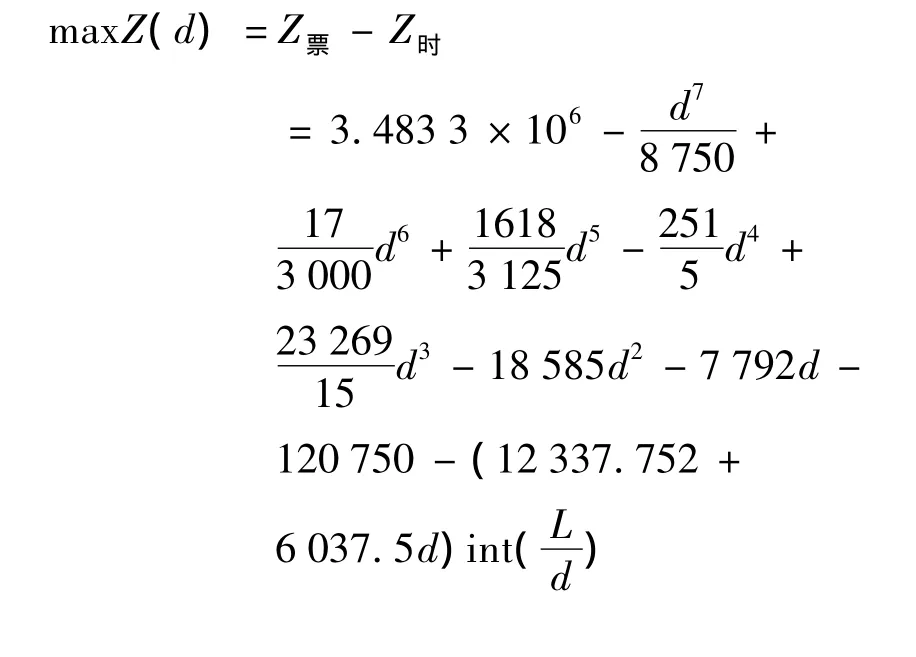
其中，

用matlab软件在d为0.3～4的区间以0.1位精度对总效益进行计算，模型中总效益与平均站间距关系如图5所示，同时得到:

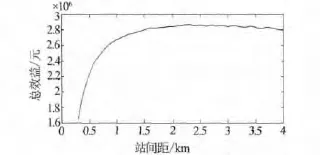
图5 模型中总效益与平均站间距的关系

3 结论

通过引入某城市的实际数据，主要从车票收入和乘客出行时间成本两方面考虑，建立了城市轨道佳通站间距优化模型，并最终应用matlab软件计算出了最大费用为287.05万元，最优平均站间距为2.3 km.从计算结果中可以看到，站间距在1.5 km以下时，效益随站间距变化的幅度很大，而站间距大于1.5 km时，效益变化的敏感度显著降低，这说明实际站间距取值的浮动范围应避免小于1.5 km.同时，随着今后研究的逐步深入、可获得数据的更加充实，相信将来还可以将诸如建设费用、运营费用以及社会效益等量化并加入到模型中来，是优化的合理性更高.

［1］王芳.基于出行方式选择的轨道交通站间距确定［J］.大连交通大学学报，2011，32(6):36-40.

［2］姚新虎.基于出行距离的快轨交通站间距的确定方法［J］.都市快轨交通，2008，21(1):48-50.

［3］王怡璇.基于出行时间的轨道交通站间距探讨［J］.甘肃科学学报，2012，24(4):127-130.

［4］李鹏.基于效益成本理论的城市轨道交通合理站间距研究［J］.铁道勘测与设计，2011(1):66-68.

［5］左大杰，王慈光.基于总出行时间最少的城市轨道交通站间距探讨［J］.铁道运输与经济，2002，25(2):23-25.

［6］魏金丽.城市轨道交通站点布局优化研究［J］.青岛理工大学学报，2008，29(4):88-93.

［7］李锋.城市轨道交通车站分布方法研究［D］.长沙:长沙理工大学，2008.

［8］张雪.城市轨道交通社会效益研究［D］.哈尔滨:哈尔滨工业大学，2011.