轮对等效锥度与车辆动态特性关系分析

张剑，王辉，王玉艳，金学松

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028;2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)*

0 引言

轮对等效锥度作为轮轨关系中的重要参数之一，对车辆临界速度和曲线通过能力都有重要的意义［1-2］.轮轨接触状态及车辆动态特性关系到车辆运行平稳性及经济性，一直受到学者的广泛关注.王开云等［3］基于轮轨耦合动力学理论，对车辆在弹性轨道上非线性临界速度进行分析，发现轨道结构振动对车辆稳定性是有影响的.温泽峰等［4］数值分析了磨耗型踏面和锥形踏面的接触蠕滑率和蠕滑力，结果表明2者差异较大.李龙［5］利用多体动力学软件建立车辆仿真模型，分析了轮轨参数对车辆临界速度的影响.孙善超等［6］分析了轮对内侧距变化对高速客车车辆动力学的影响，结果表明增大轮对内侧距可以改善舒适性、减小磨耗、提高临界速度.张剑等［7］基于CRH5型高速动车组车辆动力学参数，以欧洲标准 BSEN13715定义的锥度2.5%车轮型面为基础，通过设计不同锥度的锥形车轮踏面的动力学分析表明，踏面的锥度并不是越小越好，踏面锥度为2.0%时轮对动态横移量随速度提高而增大，并发生轮缘接触，作者认为可能是因为轮对锥度过低，恢复对中的能力不足所致.Shevtsov等［8］为了解决直线区段车辆平稳性与轮对恢复对中能力的矛盾，结合以轮对滚动圆半径差为设计目标的车轮型面优化设计方法进行了研究，结果表明等效锥度较低时轮对所需要恢复对中时间较长.黄运华等［9］利用 Simpack动力学软件分析了德国DIN5573(即S1002，并被S1002替代)和LM车轮型面对地铁车辆动力学性能的影响，认为由于踏面形状不同导致轮轨几何接触特点存在差异，尽管DIN5573踏面的车辆稳定性好于LM型踏面，但前者曲线通过性能并不理想，其中一个重要原因就是DIN5573型踏面的等效锥度较小所致［9］.

可以看出，上述文献大多以既有踏面或纯锥形踏面进行匹配研究，并不能很好地反映出轮对等效锥度对车辆动态特性的影响.本文利用改善轮轨接触状态的车轮型面几何设计方法［10］，通过设计一系列等效锥度不同的车轮踏面，和文献［7］设计的锥形车轮踏面，分析包括车辆临界速度和曲线通过性能在内的车辆动态特性.

1 等效锥度对临界速度的影响

利用Simpack/rail动力学软件，以某高速动车组车辆动力学参数［11-12］建立车辆动力学模型，对文献［7］设计的锥度0.010～0.090的锥形车轮踏面和根据文献［10］设计方法设计的等效锥度为0.030～0.090的磨耗型踏面利用时域响应法［13］计算车辆临界速度.计算时，轨距1 435 mm、轮对内侧距1 353 mm、轨底坡1/40，车轮半径430 mm.

锥形踏面车辆临界速度随锥度变化情况如图1，当设计锥度在0.010～0.025范围内时，临界速度随锥度的减小而迅速降低，锥度为0.025时临界速度约为730 km/h.注意到，当锥度小于0.025时，对临界速度影响很大，是因为轮对等效锥度过小使轮对恢复对中能力变差所致［7］.另外，对于锥形踏面来说，在轮轨接触点达到轮缘根部之前，轮对的等效锥度几乎不变，导致即使轮对发生很大横移也无法产生足够大的轮对滚动圆半径差，轮对蛇行运动失稳.

锥度在 0.025～0.065区间内，如图 1，临界速度维持在很高值且变化不大.当锥度在0.065～0.10范围内时，临界速度先是缓慢下降，在锥度为0.075处降低到约709 km/h，之后又有所回升，在0.085 处约为 729 km/h.这与文献［14］的线性临界速度与等效锥度的平方根成反比的结论出入较大.

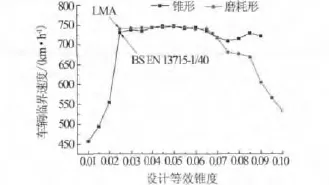
图1 轮对等效锥度对车辆临界速度影响

对于设计的磨耗型踏面，临界速度随设计等效锥度变化曲线如图2，当设计锥度大于0.070时车辆临界速度与轮对等效锥度的平方根大致成反比关系，这与文献［14］的结论基本吻合，这一规律也与文献［15］基本一致.

设计等效锥度小于0.070时，如图1，车辆临界速度与锥形踏面的结果基本相同.当设计锥度大于0.070时，临界速度则呈单调下降的趋势，与锥形踏面的结果差别越来越大.例如，当设计锥度为0.085时，锥形踏面EN4035的临界速度约为729 km/h，而设计磨耗型踏面Z121的临界速度约为669 km/h.

为分析原因，这里对EN4085和Z121进行轮轨接触分析，两种踏面的轮对等效锥度如图3.可以看出，EN4085轮对等效锥度在横移小于约6.5 mm时基本不变，而Z121轮对在横移小于约7.0 mm也变化不大，并略低于前者.也就是说虽然Z121轮对等效锥度略低于EN4085，但其临界速度反而降低了.这还需要分析它们的轮轨接触情况.

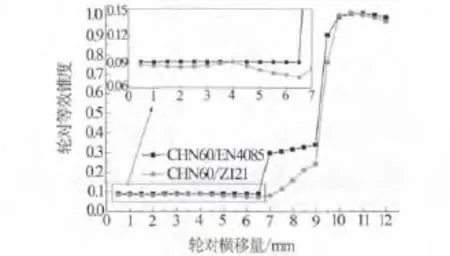
图3 轮对等效锥度比较

对于EN4085型踏面，如图4(a)，在轮对横移量小于6.5 mm时，车轮以锥形部分与CHN60钢轨型面R80圆弧右端接触.而对于CHN60/Z121，如图4(b)，轮对横移小于约4.0 mm时与钢轨顶部R300圆弧接触，横移约4.0～8.5 mm时与钢轨内侧R80圆弧右端接触.这是因为，Z121以与构成CHN60型面相似的圆弧接触，设计等效锥度越大车轮踏面与钢轨相似程度越高，亦即轮轨型面的共形程度也越高，相同横移时轮轨接触点分布较锥形踏面非常明显地分散分布.

根据文献［7］对CHN60/LMA的动力学分析，即便是在直线运行，当车辆以高速运行时，轮缘根部也会与钢轨内侧的R13圆弧部位发生动态作用.因此，在轨道不平顺的作用下，设计踏面Z121的轮缘根部比锥形踏面EN4085更容易与钢轨发生接触，形成过大的动态轮对滚动圆半径差，导致车辆发生蛇行运动，临界速度降低.

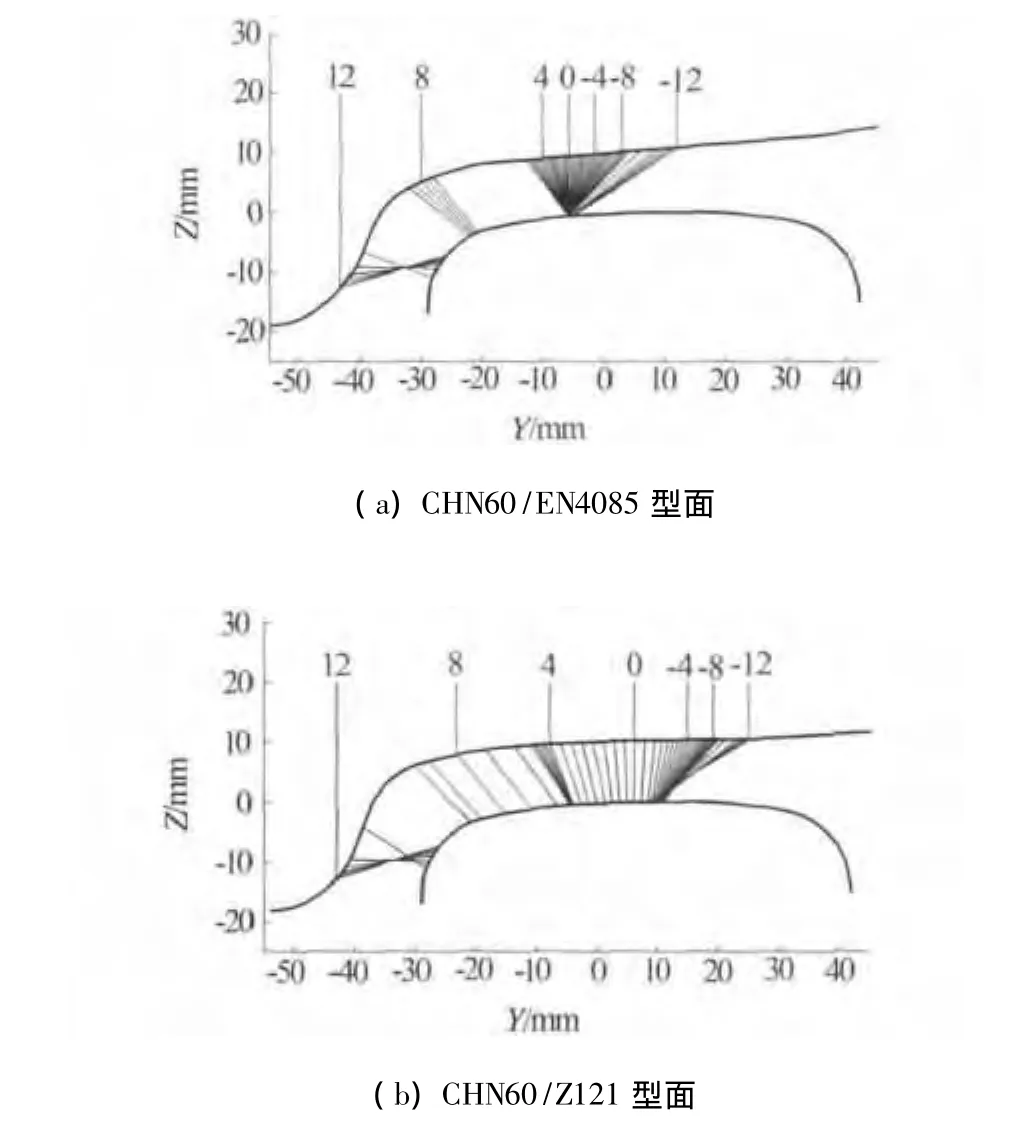
图4 轮轨型面接触点对

因此，对于磨耗型车轮踏面，随着设计轮对等效锥度提高，轮轨型面的共形程度提高，当轮对等效锥度提高到一定程度时，将导致轮轨型面共形程度过高，轮缘根部与钢轨动态作用加剧，使车辆临界速度降低.

2 等效锥度对曲线通过性能的影响

合理的轮轨匹配不仅可以使车辆具有较高的临界速度，也应该具有良好的曲线通过性能.为了进一步分析通过曲线时轮对等效锥度应具备的特点，选择临界速度较高的3个车轮踏面进行典型分析，锥度为0.035的EN035锥形踏面，设计等效锥度分别为 0.035、0.065 的 Z020、Z080.并与既有的LMA型踏面进行比对.

上述4种匹配的等效锥度随横移量变化如图5所示.注意到，在横移量小于约 7.5 mm时EN4035轮对等效锥度基本不变，在横移量约2.5～7.5 mm范围内为4者最小，当横移量达到8.0 mm时等效锥度急剧增大到约 0.257，并在 8.0 ～9.5 mm缓慢增加.Z020等效锥度在横移小于约2.5 mm时与EN4035基本相等，在2.0 ～6.5 mm范围内逐渐增大，与LMA较为相似，并略大于LMA，在横移约7.0 mm处与LMA相等.Z080轮对等效锥度明显高于其它3者，横移量小于约4.0 mm时等效锥度基不变，在约4.5 mm等效锥度增大到约0.094，随后等效锥度略高于LMA.从Z080轮对等效锥度曲线可以看出，在小横移量时等效锥度比较大，随着横移量增大等效锥度增大较快，对于车辆曲线通过比较有利.

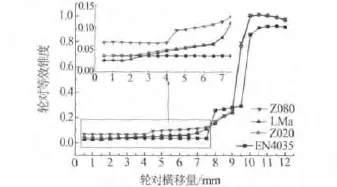
图5 轮对等效锥度曲线

2.1 通过理想曲线

影响曲线通过性能的因素很多，除轮轨型面外还包括车辆过曲线速度、曲线半径、外轨超高、缓和曲线长度等.这里考虑车辆以均衡速度通过3种半径的曲线，车辆通过曲线时的速度及曲线参数如表1.

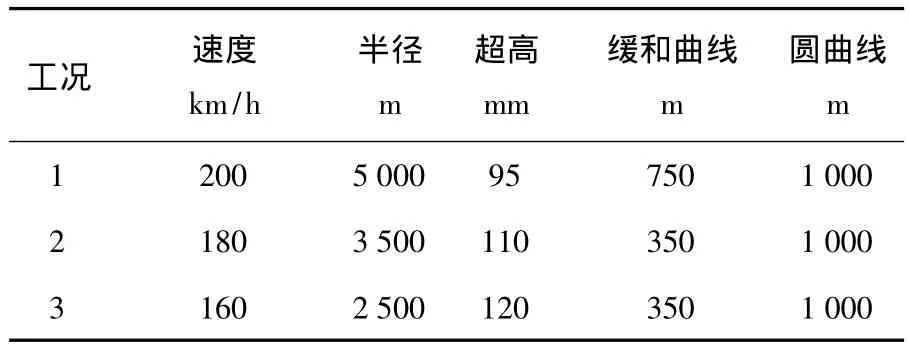
表1 曲线设置参数设置

不考虑轨道不平顺的作用时，轮对最大横移量如表2，这里轮对1为前导轮对，其它轮对从前向后依次编号.可以看出，除EN4035在工况1轮对横移量幅值从大到小依次为1、2、3、4位轮对以外，其它各情况轮对横移量最大从大到小依次均为1、3、2、4 轮对.

在3种工况下，EN4035轮对横移幅值为4者最大，Z020轮对横移量明显小于 EN4035，Z080轮对横移量又小于Z020，即曲线通过性能依次增强.与它们在轮对横移较大时等效锥度大小关系一致，如图5，等效锥度较大者轮对横移量较小曲线通过性能较好.

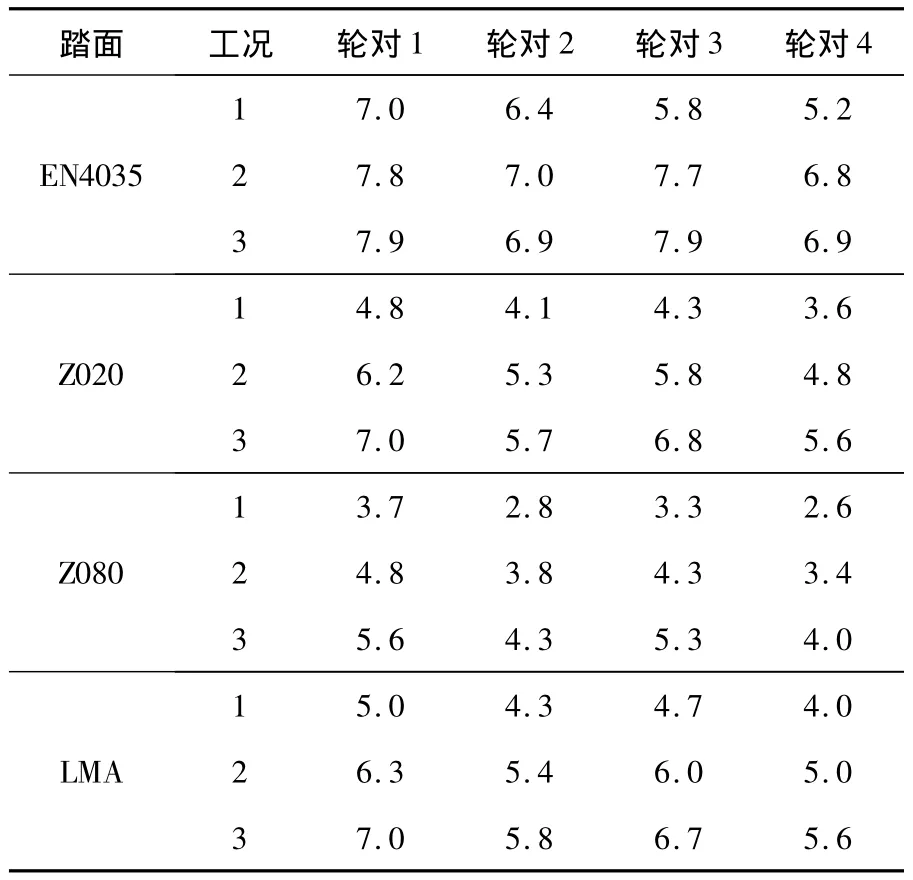
表2 轮对通过理想曲线的最大横移量 mm

2.2 考虑轨道不平顺作用时曲线通过性能

车辆通过曲线速度及曲线参数同样如表1.鉴于车辆通过曲线时车辆前导轮对工作条件最恶劣，故这里取1位轮对在圆曲线区段动态横移量进行分析，4种踏面轮对的统计结果如表3.需要说明的是，各种轮对动态横移量在圆曲线未发生正负号改变情况，即轮对向曲线外侧横移.另外，由图5可以看出4种踏面轮对的轮轨间隙并不相同，EN4035轮轨间隙约为9.5 mm，其余3者约为9.0 mm，故在分析轮缘接触情况时考虑了轮轨间隙的差异.

总体看来，对4种踏面轮对动态横移量统计结果相同的地方在于，以均衡速度通过曲线时，随着曲线半径的减小轮对横移量最小值、平均值和最大值呈逐渐增大趋势，发生轮缘接触的次数相应地明显增大，而统计方差则大致呈减小趋势.统计方差表征轮对动态横移量与平均值的偏差，方差越大说明横移量变化越大，轮轨接触不平稳.

由于EN4035是纯锥形踏面，如图5，轮对横移小于约7.5 mm时等效锥度不变，且在横移量较大时小于其它3者，故3种工况均发生了轮缘接触.Z020等效锥度在轮对横移小于约2.5 mm时与EN4035基本相等，但横移大于2.5 mm时等效锥度大于后者，故轮对动态横移量也明显小于后者，并且在通过大半径曲线时避免了轮缘接触，在通过其它2种小半径曲线轮缘接触次数较EN4035明显减少.同时注意到，Z020踏面轮对横移最小值、平均值及最大值均大体上略小于LMA，工况1、2的轮缘接触次数也低于LMA，也是由于前者在轮对横移约小于7.0 mm时轮对等效锥度略微大于LMA所致.对于Z080踏面，其轮对动态横移的最小值、平均值和最大值均小于其它3者对应工况的结果，是由其轮对等效锥度较明显地大于其它3者所决定.

值得注意的是，Z080踏面轮对除在工况3发生频次很低的轮缘接触外，前两个工况均未发生轮缘接触现象，这与其轮对横移大于约4.0 mm时等效锥度提高密不可分.另外，尽管Z020、LMA在轮对横移较小时等效锥度较小，但轮缘根部等效锥度随轮对横移而逐步增大，使得2者曲线通过性能较锥形踏面EN4035明显提高，轮缘钢轨间动力作用也明显得到缓解.

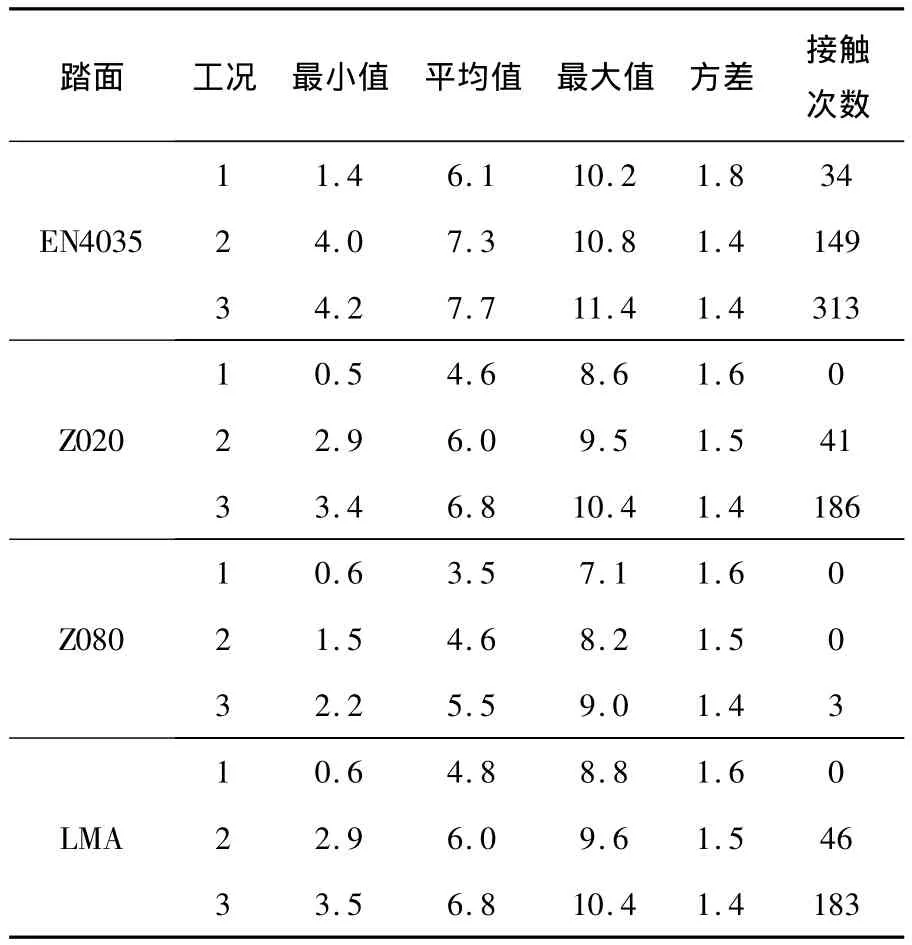
表3 前导轮对动态横移统计 mm

3 结论

通过上述设计不同等效锥度的车轮踏面分析表明，轮对等效锥度对车辆特性影响很明显，并可得到如下结论.

(1)锥形踏面分析表明，踏面锥度较小时可以获得足够高的车辆临界速度，但踏面锥度太小会使轮对恢复对中能力不足导致车辆临界速度迅速降低;

(2)车辆临界速度并不严格地与轮对等效锥度平方根成反比关系，而是存在一个小锥度范围，等效锥度在该范围内变化时临界速度变化不大，并且在该范围内磨耗型踏面与锥形踏面临界速度基本相同.等效锥度取值较大时，车辆临界速度方与轮对等效锥度平方根成反比;

(3)轮对等效锥度随轮对横移量的增大而持续增大可以提高其曲线通过性能，并有利于避免轮缘接触、缓解轮缘磨耗.

［1］严隽耄.车辆工程［M］.北京:中国铁道出版社，2009.

［2］金学松，沈志云.轮轨滚动接触疲劳问题研究的最新进展［J］.铁道学报，2001，23(2):92-108.

［3］王开云，翟婉明，蔡成标.车辆在弹性轨道结构上的横向稳定性分析［J］.铁道车辆，2001，39(7):1-4.

［4］温泽峰，金学松，刘兴齐.两种型面轮轨滚动接触蠕滑率和摩擦功［J］.摩擦学学报，2001，21(4):288-292.

［5］李龙.高速车辆运动稳定性的研究［D］.成都:西南交通大学，2008.

［6］孙善超，王成国，李海涛，等.轮轨接触几何参数对高速客车动力学性能的影响［J］.中国铁道科学，2006，27(5):93-98.

［7］张剑，金学松，孙丽萍，等.基于CRH5高速动车组车辆的轮对动态特性与等效锥度关系初探［J］.铁道学报，2010，32(3):20-27.

［8］SHEVTSOV I Y，MARKINE V L，ESVELD C.Design of railway wheel profile taking into account rolling contact fatigue and wear［J］.Wear ，2008，265(9-10):1273-1282.

［9］黄运华，李芾，傅茂海，等.踏面形状对地铁车辆动力学性能的影响［J］.机车电传动，2007，10(1):39-41.

［10］张剑，王玉艳，金学松，等.改善轮轨接触状态的车轮型面几何设计方法［J］.交通运输工程学报，2011，11(1):36-42.

［11］REN Z，SUN S，XIE G.A method to determine the two-point contact zone and transfer of wheel-rail forces in a turnout［J］.Vehicle system dynamics，2010，48(10):1115-1133.

［12］张曙光.高速列车设计方法研究［M］.北京:中国铁道出版社，2009:77-94.

［13］翟婉明.车辆/轨道耦合动力学［M］.3版，北京:科学出版社，2007:337-350.

［14］王福天.车辆系统动力学［M］.北京:中国铁道出版社，1994:24-58.

［15］CUI DABIN，LI LI，JIN XUESONG，et al.DING JUNJUN.Influence of vehicle parameters on critical hunting speed based on ruzicka model［J］.Chinese Journal of Mechanical Engineering，2012，25(3):536-542.