自动螺丝锁付机器人控制系统研究及路径优化

王德会，王喜顺，方海涛，罗昌杰，王书付

(1.华南理工大学 机械与汽车工程学院，广州 510642;2.中国科学院 深圳先进技术研究院，广东深圳 518055)

0 引言

自动螺丝锁付机器人由于其可实现自动组装，生产效率高，生产成本低等优点被广泛的使用于汽车零部件生产、电脑、显示屏、手机等领域。目前的自动螺丝锁付机器人对夹具定位工件精度要求高，不能自行校正螺丝孔位偏差，而且没有进行螺丝锁付路径优化，对于规则，种类单一的工件，该类设备能够做到稳定可靠地工作［1-2］;但对于形状不规则、种类较多，夹具无法做到精确定位的工件，目前的设备还不能高效准确稳定的实现锁付。所以为了提高锁付的准确度和效率，本文结合HexSight 图像处理软件，提出基于视觉定位的偏差补偿算法，自行校正螺丝孔位偏差，并分析了传统遗传算法的优势及缺陷，提出了改进遗传算法对螺丝锁付路径进行优化，并给出两种算法路径优化图，这种方法还可以应用到其他路径优化问题。

1 螺丝锁付机器人的工艺流程

自动螺丝锁付机器人工作流程一般分为两个系统:送料系统和螺丝锁付系统。先将螺丝倒入自动螺丝排列机中，排序后的螺丝将由压缩空气高速吹至螺丝刀头，最后由电批锁入产品中。

螺丝锁付工件如图1 所示。

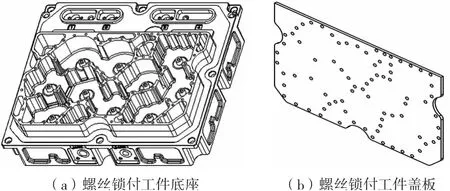
图1 螺丝锁付工件模型图

2 控制系统硬件设计

本控制系统采用“PC 机+泓格PIO-D96 数字量输入输出卡+CCD 摄像机”开放式运动控制方法，PC 机为控制系统的中心部分，CCD 摄像机用于对螺丝锁付孔位置精确反馈，PIO-D96 负责整个运动控制系统的完成。控制系统结构如图2 所示。

图2 控制系统结构图

3 工件位置偏差补偿算法

在工作中由于夹具无法对工件精确定位或电批旋转扭力的作用引起工件的位置发生偏转，从而造成锁付不准确，需要人工二次锁付，有的甚至损坏工件，大大降低工作效率，增加生产成本，所以锁付过程中自行校准孔位偏差对整个系统运行的稳定性及准确性是至关重要的。

3.1 视觉识别系统软件设计

为了满足自动螺丝锁付机器人对锁付螺纹孔高精度定位要求，在机器视觉部分，对CCD 摄像机采集图像采用基于美国Adept 公司高性能机器视觉软件开发包HexSight 在Microsoft Visual studio 2008 中的二次开发进行分析处理。通过引入HexSight 提供的具有丰富图像处理资源的ActiveX 控件，对CCD 摄像机进行标定，建立待识别对象模式库，配置所需的子模块及各种定位功能子模块，完成对象轮廓几何特征的搜索和提取［3-5］。如图3 所示，为视觉系统在工件某个位置的图像识别效果。

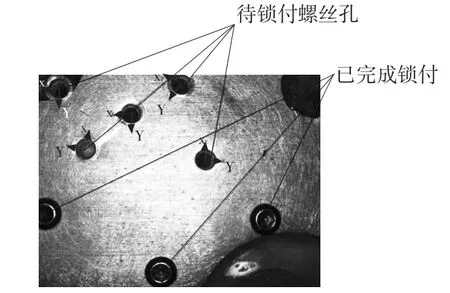
图3 视觉识别测试图像

从图3 可以看到，无论待锁付螺纹孔及锁付完毕螺纹孔位置相对关系如何，该视觉识别系统都能准确识别出待锁付螺纹孔位置(待锁付螺丝孔中心显示蓝色坐标)，且不会出现误识别情况。由此可以得出本文所建立的识别对象模式及相关参数配置准确可靠。

3.2 位置偏差补偿算法

工件位置偏差主要由平移偏差和旋转偏差组成，工件平移偏差可以通过视觉识别采集点坐标值，然后计算理论值与真实值之间的偏差得到平移偏差补偿值。旋转偏差的计算以平移偏差补偿为基础，即工件的实际坐标原点值与理论坐标原点值重合。图4 显示了工件向左及向右旋转两种情况。

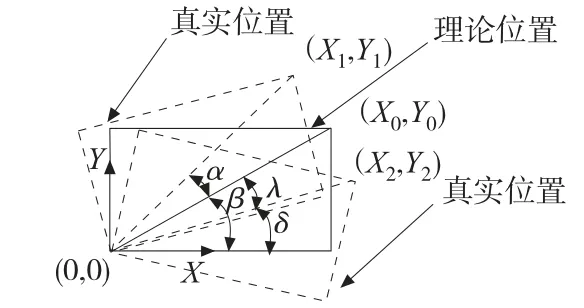
图4 工件左右旋转偏差示意图

向左旋转时，工件右上角坐标值由(X0，Y0)变为(X1，Y1)，根据对应几何关系及对所得式化简，得到下式:

式中，α 为工件相对坐标原点旋转角度。

在自动螺丝锁付机器人工作过程中，由视觉识别系统采集准确的坐标值(X1，Y1)，根据已知坐标值(X0，Y0)，结合式(1)(2)及对应关系可得到:

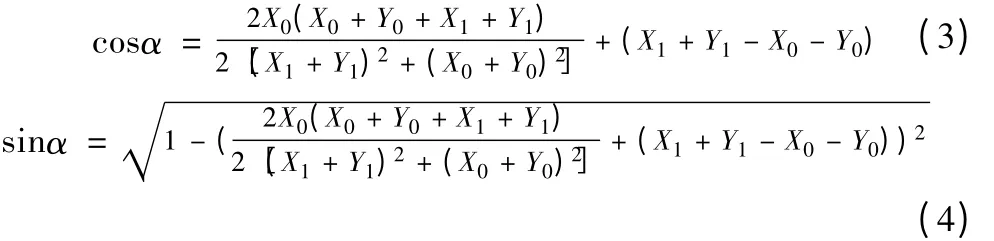
式(3)、(4)计算出工件旋转的偏差量，那么根据已知的理论坐标值和计算出来的偏差量，代入公式(1)、(2)就可以得到工件任意螺纹孔i的实际坐标值(X1，Y1)系统可根据实际坐标值对工件坐标纠正更新，同时在工作过程中定期读取螺纹孔坐标信息，对有偏差的坐标及时进行更新补偿。

而向右旋转时，则可简化为由点(X2，Y2)向左旋转λ 至(X0，Y0)，利用向左旋转情况联合(1)、(2)、(3)、(4)式计算出工件上所有螺纹孔向右偏转的实际坐标值。

基于视觉识别的位置偏差补偿算法有效的校正了工件锁付过程中产生的位置偏差，使得锁付过程准确无误，而且夹具对工件不需要高精度的定位，提高了效率。

4 螺丝锁付路径优化

为了提高螺丝锁付效率，就要对螺丝锁付路径进行分析优化。螺丝锁付路径优化问题可以转化为典型的TSP 问题，遗传算法是求解该问题比较有效的方法之一［6］，它克服了传统优化算法容易陷入局部极小值的缺点，是一种全新的优化算法。遗传算法有许多优点，但它存在收敛速度慢、早熟等缺陷［7］。为了改进遗传算法的效果，许多研究者提出了不同的改进方法，文献［8］提出了贪婪随机自适应搜索过程产生初始群体，这样初始群体有较好的质量;文献［9-10］提出通过改变遗传算法的交叉或变异算子来改善遗传算法的优化结果。

基于传统遗传算法所具有的优势及不足，提出一种改进的遗传算法来解决螺丝锁付点路径优化问题，结果表明，改进后的遗传算法优化结果比标准的遗传算法优化结果有了一定的改进，其结果更接近理想值。

4.1 遗传算法的改进

(1)初始群体的产生

标准遗传算法中，初始群体是随机产生的，而初始种群的质量会影响到群体演化过程的效率和解的结果，所以本文使用贪婪随机自适应搜索过程来产生初始群体，这样既能保证初始群体的多样性，又能保证初始群体有着较好的质量。

(2)自适应调整交叉概率和变异概率

传统的遗传算法使用的是固定的交叉概率和变异概率，不变的交叉概率和变异概率严重影响算法的收敛效果，所以本文根据个体的具体情况，自适应地改变Pc、Pm的大小。自适应参数调整方案如下［10］:

式中，fmax为某代中最优个体适应度;为此代平均适应度。

本文设计的适应度函数为

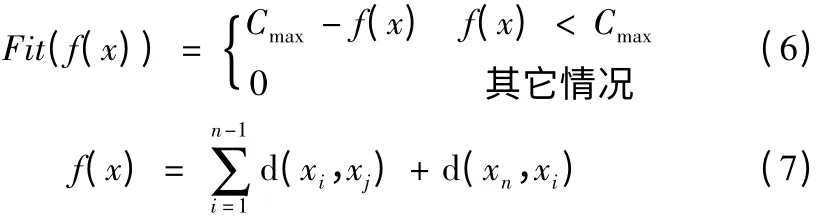
式中，d(xi，xj)是两点间的距离，系数Cmax是一个适当的相对比较大的数，是f(x)的最大值估计，可以是一个适当的输入值。

(3)适应度值标定

在初始群体中，可能会出现某些个体适应度值很大，为了防止结果收敛于局部最优解，就要限制它们的繁殖;在计算接近结束时，群体中的个体适应度值很接近，很难继续优化，解会在最优解附近摇摆，这时候就要放大个体适应度值，提高选择能力。适应度值标定的计算公式如下［10］:

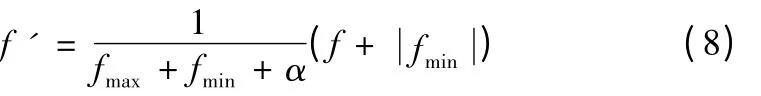
式中，f为原适应度值，fmax、fmin分别为适应度值的上下界，α 为开区间(0，1)内的一个正实数。

(4)贪婪两点互插入变异算子

在最优路线中，大部分点都是与其比较近的点相邻的，所以可以根据这一实验结果采用贪婪两点互插入变异算子。也就是说，在所有的个体中随机选择一个点c，在点c的左右两边分别插入与c最近的点c1 和c2。具体操作如下:如果在个体c左右两边的点都与c1，c2 不同，则将c1 与c左边的点调换，c2 与c右边的点调换;如果有相同的点就改变不同的，这样得到的新个体的适应度若小于原个体的适应度，就用新个体替代原个体。

(5)动态顺序插入交叉算子

大量实践发现，一个好的交叉算子能够使群体快速地达到最优解，反之，效果就不是很理想。本文使用动态顺序插入交叉(DO IC)算子:将两个待交叉的染色体一个当作基本染色体，另一个作为参考染色体，根据参考染色体中点与点之间的邻接顺序，采用三角距离差函数作为评价标准，运用贪婪策略思想，随机动态地调整交叉步长，改变染色体的编码顺序，以此提高子代染色体的适应度。

4.2 螺丝锁付点路径优化模拟

现有79 个螺丝孔需要锁付，为了提高锁付效率，分别使用传统遗传算法和改进遗传算法对它的路径进行优化，如图5、图6 所示。

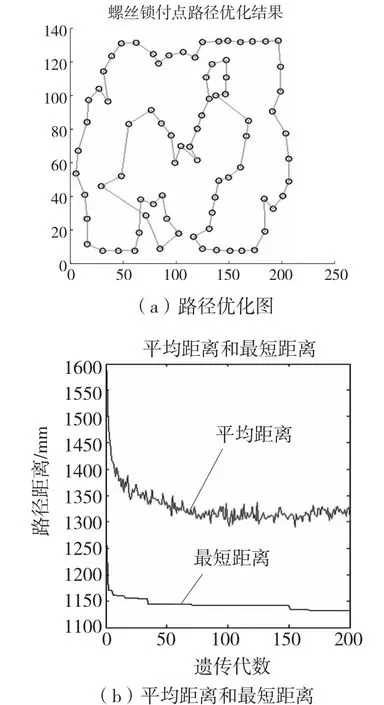
图5 标准遗传算法路径图

图6 改进遗传算法路径图

如图5 所示，使用标准遗传算法对螺丝锁付路径进行优化，其最短距离为1139mm，但路径图有交叉的地方，同时优化结果有早熟的趋向。而采用改进型遗传算法如图6 所示，得到路径最优解为1103mm，其优化计算后得到的优化路径为:53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 70 71 32 31 30 29 28 27 69 26 25 24 23 22 21 20 19 18 17 16 14 15 13 12 11 10 9 8 7 79 78 77 76 75 74 73 72 33 34 35 36 37 38 39 40 41 42 43 46 45 47 48 49 6 5 44 4 3 2 1 50 51 52。

使用改进遗传算法得到的优化结果比标准遗传算法得到的结果理想很多. 改进之后其路径已经没有交叉部分，其最短距离也缩小了36mm，更接近最优结果。同时改进之后优化结果早熟的趋向得到了一定的改善。所以经过改进遗传算法优化之后螺丝锁付路径已经非常接近最优解了，这个优化路径对实际应用有很大的指导意义。

5 结论

采用改进遗产算法优化螺丝锁付路径，结果表明，改进后的遗传算法优化结果比标准的遗传算法优化结果有了一定的改进，其结果更接近理想值，早熟问题也得到改善。经过优化后螺丝锁付路径达到了理想的状态，螺丝孔锁付效率更高。基于视觉识别的自动螺丝锁付机器人对需要螺丝锁付工件偏差能够进行自行纠正补偿，显著提高了螺丝锁付准确性和稳定性。

［1］姚文钦，谈士力 高速自动拧螺丝系统研究［J］.机电一体化2009，15(11):1 -4.

［2］蔡军爽.螺丝机控制系统研究与开发［D］. 沈阳:东北大学.2008

［3］ Adept Technology Inc.，" Hexsight Reference Manual，v3.3，"2009，279 -382.

［4］吴文琪，孙增圻.机器视觉中的摄像机标定方法综述［J］.计算机应用研究，2004，21(2):1 -3.

［5］贾云得.机械视觉［M］.北京:科学出版社，2000.

［6］Jean-Yves Potvin. Genetic algorithms for the traveling salesman problem［J］. Annals of Operations Research，1996(63):339 -383.

［7］雷英杰，张善文，李续武，等.MATLAB 遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2009.

［8］YANNIS MARINAKIS，ATHANASIOS MIGDALAS，PANOS M. PARDALOS. A Hybrid Genetic—GRASP Algorithm Using Lagrangean Relaxation for the Traveling Salesman Problem［J］. Journal of Combinatorial Optimization，2005(10):311 -326.

［9］Masafumi Kuroda ，Kunihito Yamamori etal. Development of a novel crossover of hybrid genetic algorithms for large-scale traveling salesman problems［J］. Artif Life Robotics，2010(15):547 -550.

［10］Fang-Geng Zhao，Jiang-Sheng Sun，Su-Jian Li etal. A Hybrid Genetic Algorithm for the Traveling Salesman Problem with Pickup and Delivery［J］. International Journal of Automation and Computing，2009，6(1):97 -102.