几种单因素实验设计在体育科学中的应用研究 *

游永豪 温爱玲



几种单因素实验设计在体育科学中的应用研究*

游永豪1温爱玲2

(1.合肥师范学院体育科学系，安徽 合肥 230601；2.淮南师范学院体育系，安徽 淮南 232038)

单因素实验设计方法目前在体育科学实验研究中经常使用。探讨了单组设计、完全随机设计、随机区组设计、拉丁方设计、交叉设计等几种单因素实验设计的统计分析方法，并对其统计分析特点进行了分析。

实验设计；统计分析

通过查阅2000年至2012年《体育科学》、《北京体育大学学报》、《体育与科学》三种体育类、人文社会科学类核心期刊中728篇运动人体科学方面的实验研究性论文，发现78.6%的论文采用的是单因素实验设计。然而，单因素实验设计中统计分析方法应用合理的只占28.2%。由此可见，体育科学研究中，统计分析方法使用技术严重缺乏，如何应用合理的统计分析方法发现数据变化的规律性是目前众多体育科研人员亟待解决的问题之一。本研究旨在探讨单因素实验设计的统计分析方法。

1 单组设计

1.1 单组设计因素的安排

单组设计是最简单的实验设计方法，其因素只有一个——重测因素。单组设计中，一般研究者关心的是实验因素随重测因素（如时间、对称部位等）的变化规律。如表1所示。

表1 单组设计方案

受试对象重测因素 t1t2……tk 1t11t21……tk1 2t12t22……tk2 …………… nt1nt2n……tkn

表1为n个研究对象（同一组）进行k次重复测量的因素安排方案。t1、t2、……、tk分别为重测因素的k个水平。

（1）没有设计对照组使实验实施起来更加容易，受试对象更容易控制。但是，却不能排除与自变量同时出现的附加变量的影响。例如实验周期比较长时，研究对象本身的自然变化（如身高、体重的变化；女性生理周期等）、偶然因素（天气、疾病等偶然因素）等附加因素会和实验因素一起作用于研究对象，由于没有设立对照组，这些自然因素、偶然因素与实验因素的效应便无法区分。（2）重测时间间隔相同或测量部位对称，很好的控制了成熟因素对内部效度的影响。但是，由于不易充分控制测验与实验处理的交互作用，会降低实验外部效度。（3）多次重复测量可以很好的控制测验因素的干扰，但是多次进行同样的测试往往也会降低或增加研究对象对实验处理的敏感性，从而影响到实验结果[1]。由此可见，单组设计的优点与缺点共存，互相制约。

1.3 单组设计的统计分析方法

如果各次测量值服从正态分布，重测次数k=2时，一般采用配对t检验；k≥3时，采用重复测量的方差分析或Hotelling T2检验。如果各次测量值不服从正态分布，重测次数k=2时，一般采用Wilcoxon符号秩检验；k≥3时，采用Friedman检验（Friedman 双向评秩方差分析）。

2 完全随机设计

2.1 完全随机设计因素的安排

完全随机设计又称为成组设计，是采用随机化分组的方法将同质的实验对象分配到各处理组，各组分别接受不同的处理。各组样本含量相等时，称平衡设计；不等时，称非平衡设计。平衡设计时检验效率较高。设计方案如图1。

图1 完全随机设计方案图

可见，对照组可以不止一个，同时可设置空白对照、阴性对照、阳性对照等等。各处理组应达到均衡一致，且同期平衡进行。

2.2 完全随机设计的特点

完全随机设计的特点是：设计方法简单，易于实施应用，处理组数和各样本含量都不受限制，统计方法也相对简单，实验对象发生意外时，信息量损失小于其他设计；但是本设计单纯依靠随机分组的方法对非处理因素进行平衡，缺乏有效的控制，特别是小样本时，可能均衡性均较差，引起抽样误差较大[2]。所以完全随机设计对个体间的同质性、实验的同时性等要求较高。

2.3 完全随机设计的统计分析方法

对完全随机设计资料进行统计分析时，需根据数据的分布特征选择方法。对于正态分布且方差齐性资料，处理因素只有两个水平时采用独立样本t检验，处理因素多于两个时采用单因素方差分析；对于非正态分布和方差不齐的资料，可对变量进正态行变换后再进行上述参数检验或采用非参数Mann-whitney U检验的Kruskal-Wills H检验。

3 随机区组设计

3.1 随机区组设计的特点

随机区组设计又称为随机单位组设计或配伍组设计，通常是现将实验对象按性质（如性别、体重、身高等非处理因素）相同或相近者组成区组，再分别将各组内的实验对象随机分配到个处理或对照组。设计时应遵循“单位组间差别越大越好，单位组内差别越小越好”的原则。随机区组设计方案如图2。

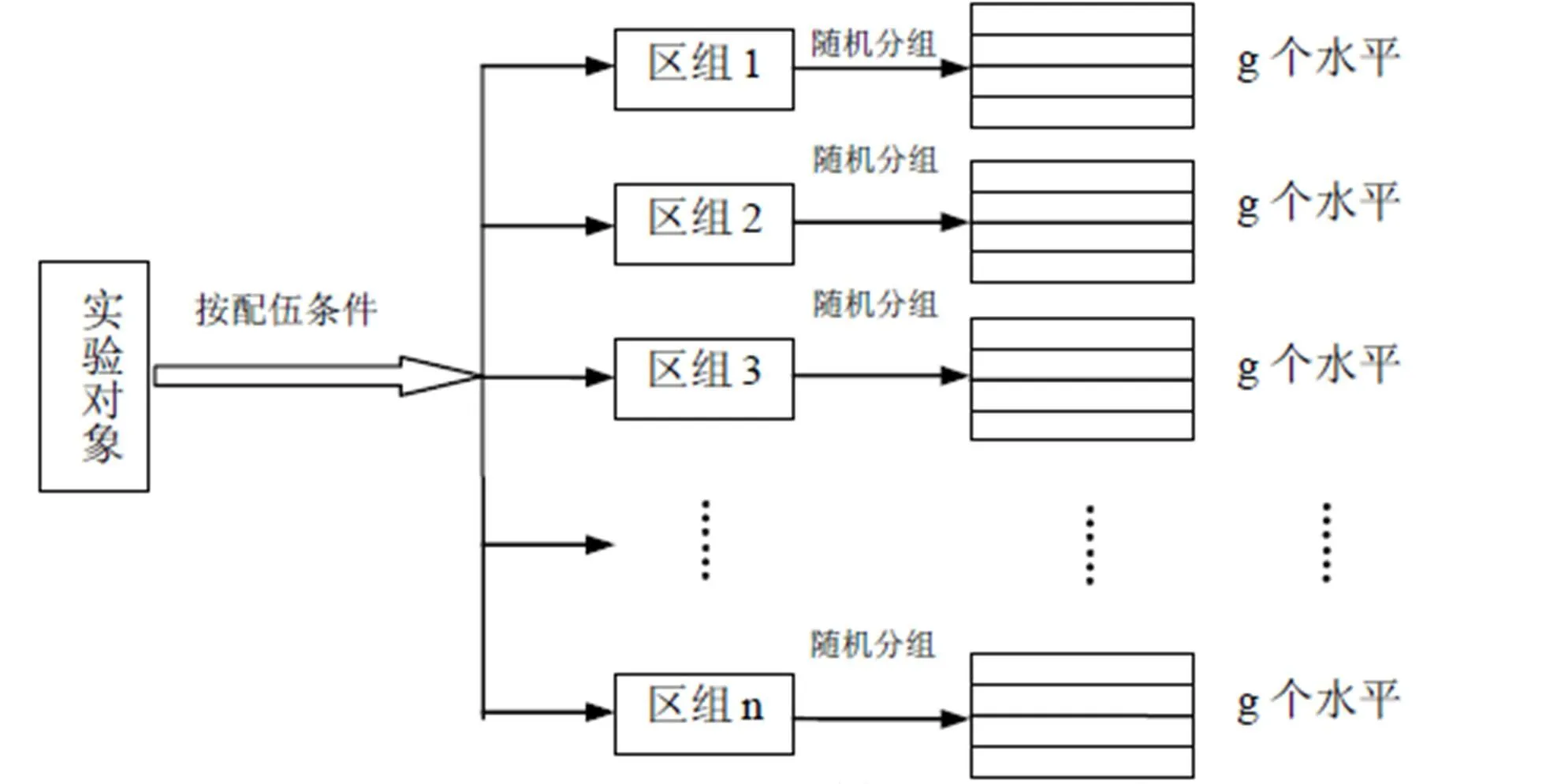
图2 随机区组设计方案图

可见，随机区组设计是单向区组化技术，随机分配的次数要重复多次，每次随机分配都对同一区组内的实验对象进行，且各处理组实验单位数量相同，区组内均衡。

3.2 随机区组设计的特点

随机区组设计的特点是：区组处理使各处理组受试对象不仅数量相同，而且提高了处理组间的均衡性，统计处理时将区组变异从组内变异中分离出来，减少了误差均方，从而使处理组间的P值更容易出现显著，提高了检验效能[3]；但是如果区组因素选择不当，由于区组因素占用了n-1个自由度，反而会增大误差均方，从而降低处理组的检验效能，并且，实验过程中若造成一个数据缺失，该区组的其他数据也就无法使用，缺失后的信息将无法弥补。

3.3随机区组设计的统计分析方法

对随机区组设计资料进行统计分析时，对于正态分布且方差齐性资料，只有两个区组时采用配对t检验，区组数多于两个时采用两因素方差分析；对于非正态分布和方差不齐资料，可对变量进正态行变换后再进行上述参数检验或采用非参数的Wilcoxon检验或Friedman M检验等。若将区组作为另一处理因素的不同水平，随机区组设计等同于无重复的两因素设计。需要注意的是，在实际科研当中，无法考查随机区组设计的正态性和方差齐性，因为随机区组设计中，每个单元格只有一个元素，但是要根据专业知识和经验对正态性和方差齐性进行判断。

4 拉丁方设计

4.1 拉丁方设计的特点

用g个拉丁字母排成g行g列的方阵，使每行、每列中每个字母都只出现一次，这样的方阵称g阶拉丁方或g×g拉丁方（Latin square）。拉丁方设计（Latin square design）是按拉丁方的行、列、拉丁字母分别安排3个因素，每个因素有g个水平。一般将g个字母分别表示处理的g个不同水平，g行表示g个不同区组（行区组），而g列表示另一个区组因素的g个水平（列区组）。因此，拉丁方设计是单向的区组化技术[4]。控制了两个非研究因素的变异。以4×4拉丁方设计的步骤和随机分配表见表2和表3。

可见拉丁方设计要求是：必须是三个实验因素，且三个因素的水平数相等；行间、列间、处理间均无交互作用；各行、列、处理的方差齐性。

4.2 拉丁方设计的特点

拉丁方设计的特点是：它控制了两个非处理因素，进一步缩小了实验误差，可以得到比随机区组设计更多一个因素的均衡，因而误差更小，效率更高，而且可以大大减少实验次数，尤其适合动物实验和实验室研究；但是要求处理数必须等于拉丁方的行（列）数，一般实验很难满足此条件，而且数据缺失会浪费大量信息，也会增加统计分析的困难。

表2 4×4拉丁方行变换、列变换

4.3 拉丁方设计的统计分析方法

对符合拉丁方设计要求的资料进行统计分析时，应采用三因素方差分析，总变异分解为处理组变异、行区组变异、列区组变异和误差变异，不能分析各因素间的交互作用[5]。分析行、列区组变异目的是使处理组变异更容易出现显著性。

表3 拉丁方随机分配表

拉丁字母ABCD 随机数27092486 秩次3124 分配结果丙甲乙丁

注：分配结果：A代表丙，B代表甲，C代表乙，D代表丁。

5 交叉设计

5.1 交叉设计的特点

交叉设计是按事先设计好的实验次序，在各个时期对研究对象先后实施各种处理，以比较各处理组间的差异。交叉设计的受试对象可以采用完全随机设计或随机区组设计方法来安排。交叉设计最简单的形式是完全随机分组的二阶段交叉设计——2×2交叉设计。设有A和B两种处理，首先把受试对象完全随机分为两组，第一组在第Ⅰ阶段接受A处理，在第Ⅱ阶段接受B处理，实验顺序为AB；第二组则相反，在第Ⅰ阶段接受B处理，在第Ⅱ阶段接受A处理，实验顺序为BA。交叉设计方案如表4。

表4 2×2交叉设计方案

受试对象准备期 阶段Ⅰ 洗脱期 阶段Ⅱ 第一组(n1)自然状态→处理A→无处理→处理B 第二组(n2)自然状态→处理B→无处理→处理A

其中准备期指实验对象经过一段时间不加任何处理的观察，确认已进入自然状态，可以进行实验；处理期（阶段Ⅰ和阶段Ⅱ）是按照设计好的实验顺序，在各个时期同时施加相应的处理；洗脱期是阶段Ⅰ后，停一段时间等处理效应消失，实验对象又回到自然状态，保证后一时期的处理结果不受前一时期处理的影响，即没有延滞作用。

当然，还有复杂一些的三阶段（3×3）、四阶段（4×4）交叉实验设计。随机分组的组数、阶段数要与处理数相同。表5是以拉丁字母代表不同的处理，以行代表不同的组别，以列代表不同的阶段描述2×2、3×3、4×4交叉设计方案。

不难看出，交叉设计实际上是拉丁方设计的重复观察，是成组设计和自身配对设计的综合应用。不过，它不需要行变换（组别随机化），只需要列变换（实验顺序的随机化），变换后第一列为阶段Ⅰ，第二阶段为阶段Ⅱ，依次类推。同时，交叉设计的应用条件也得到了严格限制，首先，交叉设计中各处理方法不能相互影响，并列两次处理之间必须有适当的间隔——洗脱阶段；其次，交叉设计实验应采用双盲法观察；最后，不宜用于自愈倾向或病程较短的疾病研究，一般适用于目前尚无特殊治疗而病情缓慢的慢性病患者的对症治疗研究。

表5 2×2、3×3、4×4交叉设计方案

5.2 交叉设计的特点

交叉设计的特点：一是节约样本含量；二是能够控制个体差异和时间对处理因素的影响，提高了检验效能；三是每个受试对象先后都接受了同样多的处理，均等地考虑了受试对象的利益。但是处理时间不能太长，而且受试对象缺失时，后一阶段的处理没法进行，会造成数据信息缺失，增加统计分析的难度。

5.3 交叉设计的统计分析

对符合交叉设计要求的资料进行统计分析时，和拉丁方设计类似，应采用三因素方差分析，总变异分解为处理间变异、阶段间变异、个体间变异和误差变异，不能分析各因素间的交互作用[6]。阶段间变异、个体间变异都是从组间变异分离出来，使处理组间变异更容易达到显著性。

6 讨论

单组设计是最简单的实验设计方法，不需设立对照组，多用于研究对象稀缺的实验研究。如某项目优秀运动员、优秀教练员等。实验设计中要注意控制附加变量的影响。统计分析时不可用多个配对t检验代替重复测量方差分析或Hotelling T2检验，以免导致Ⅰ型错误（假阳性错误）增多。

完全随机设计可以设立一个或多个对照组，但是，由于其单纯依靠随机分组的方法对非处理因素进行平衡，很容易导致随机误差过大的现象。所以一般样本量太小时不宜使用此实验设计方法。统计分析时要根据正态性、方差齐性来选择不同的统计分析方法。

随机区组设计、拉丁方设计、交叉设计都是对非实验因素进行设计和统计控制的实验设计方法。不像完全随机设计一样，只用“随机分组”的方法控制非实验因素。它们用不同的设计手段使非实验因素在各处理组间达到高度均衡，统计分析时又分离出非实验因素变异，使处理组间变异更容易出现显著性。

[1] 张力为.体育科学研究方法[M].北京：高等教育出版社，2002.

[2] 孙振球.医学统计学[M].人民卫生出版社.2008.

[3] 颜虹.医学统计学[M].人民卫生出版社.2006.

[4] 罗达勇,汪海燕,祁国鹰.体育统计方法系列讲座十三统计设计在体育科研中的应用[J].北京体育大学学报.2001,24(1).

[5] 仲晓波.拉丁方实验设计涉及的统计学原理以及使用中的几个问题[J].社会学理论及方法学研究[J].南开大学法政学院学术论丛.2002（s2）:127-130.

[6] 张文彤.SPSS统计分析高级教程[M].高等教育出版社,2006.

Research on Applying Several Single-factor Experiment Design in Sports Science

YOU Yong-hao,etal.

（PE Department of Hefei Normal University, Hefei 230601, Anhui China）

This paper discussed several statistical analysis methods of single-factor experimental design such as single-group design, completely randomized design, randomized block design, Latin square design, crossover design, and analyzes the characteristics of the statistical analysis.

experimental design; statistical analyze

2013年高校省级自然科学研究一般项目，项目编号：KJ2013B218；2013年合肥师范学院产学研重点项目，编号：2013cxyzd08。

游永豪（1982-），男，河南开封人，助教，研究方向：体育统计方法研究与实践。