一种基于改进型混合遗传算法的地-井TEM多参数反演方法

杨 毅 ， 邓晓红 ， 张 杰 ， 武军杰 ， 王兴春

(中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000)

0 引言

遗传算法是一种不依赖于问题具体领域的求解非线性、多模型、多目标等复杂系统优化问题的通用框架，多年来已经广泛应用于函数优化、自动控制、图像处理、模式识别、地球物理反演、神经网络等技术领域，并且取得了巨大成功。最早由Botelho[1]、Malcolm[2]将遗传算法应用于地震数据处理，之后陶春辉等[3]、张厚柱等[4]、F. Boschetti等[5]也做了遗传算法应用于地震波速反演的尝试， W.G. Wilson 等[6]将遗传算法用于地震剩余静校正，Fabio等[7]做了地震折射数据的反演，王兴泰等[8]、罗润林等[9]做了电测深数据的反演，师学明等[10]将遗传算法应用于大地电磁反演，谭永基等[11]对多电极电阻率测井、二维大地电磁、地下水含水层渗透系数等地球物理问题进行了反演，何伟兵等[12]讨论了小生境遗传算法及其在地球物理反演中的应用，谢维等[13]研究了混合遗传算法在大地电磁一维反演中的应用。

前人在遗传算法应用于地球物理反演上做了很多工作，取得了很好的反演效果。作者将此种算法应用于地-井TEM三分量数据处理解释，依据C. T. Barnett[14]、Fullagar[15]提出的等效电流环来描述井中TEM响应的反演方法，简化地-井TEM响应模型为自由空间中的电流环，通过对电流环的反演，确定异常的空间坐标、空间尺度和延伸方向等参数，达到地-井TEM快速、定量反演的目的。

1 等价模型描述

图1 薄板感应电流Fig．1 Induction current of plate

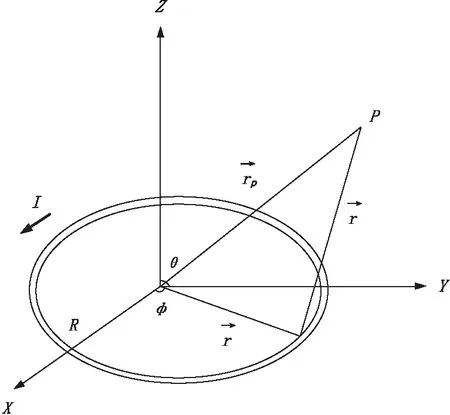
图2 载流环在空间任意一点产生的场Fig．2 Electromagnetic field of current ring in free space

以简单和实用的自由空间中导电薄板为例，依据一次场关端后薄板的感应原理(图1)，不同延时的瞬变电磁响应，可以用不同强度和半径的电流环来表示，于是某一时刻的响应，可等价为具有空间角度、半径、电流强度的圆形电流环[14-16](图2)，其三分量数学表达式如下：

(1)

(2)

(3)

其中：Bx、By、Bz为x、y、z方向上的磁场响应；R为电流环半径；I为电流强度；μ为自由空间磁导率；r为计算点至电流环中心的距离，电流环和空间计算点的角度关系r又是计算点空间坐标、电流环中心、电流环空间角度的函数，可表示为：

r=f(x,y,z,x0,y0,z0,θ1,θ2)

(4)

其中：x0、y0、z0为电流环中心坐标；θ1、θ2为表征电流环空间形态的两个空间角度。

从磁场分量表达式可以看出，用等效电流环描述的模型需要反演七个参数才能表征板体的状态，且不同参数对于场值的贡献差异巨大，使用传统的最小二乘法，偏导数矩阵严重奇异，不能很好求解，而使用遗传算法，则可以避免这个问题，同时因为遗传算法是全空间搜索方法，使用遗传算法可以解决反演初始模型偏离真值较大而导致反演不收敛的问题。

2 遗传算法改进方案

虽然遗传算法相对于传统反演方法优势在于无需求取偏导数，是全局优化方法，但是传统的遗传算法，也存在一些问题，最突出的表现就是算法在多次迭代之后，易陷于局部收敛而早熟，这个问题在多元多峰值函数求极值问题中尤其突出，作者依据简化的地-井TEM模型所建数学模型表达式即属于这类多元多峰函数求极值问题，因此必须在传统算法的基础上改进才能避免早熟，作者通过实际试算比较，最终选择逐步缩小搜索范围和多重小生境算法相结合的混合遗传算法对电流环七参数进行反演，取得良好效果。

2.1 逐步缩小搜索范围反演的方法

根据作者反复试算发现，在传统遗传算法下，多参数反演的结果不能收敛到真值，而是以真值为中心，左右波动，于是作者有了这样的考虑，以上一次搜索所得值为中心，给定更小的搜索范围，再次反演，依此进行，直到反演达到所设精度。但是，怎样来逐次设定搜索范围呢？是否每个参数都一样？针对本文的模型，通过正演计算发现，各个参数对于反演灵敏度差异较大，总的来说，电流环强度与响应值是正比关系，因此对响应影响较大，对反演影响最大，其他参数影响较小，通过总结给定如下公式：

(5)

(6)

2.2 小生境技术

小生境技术的基本思想是将生物学中的小生境概念应用于进化计算中，将进化计算中的每一代个体划分为若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群，再在种群中以及不同种群中之间杂交、变异产生新一代个体群，同时采用某种机制(预选择或排挤或分享)完成任务。

作者选择了比较两个个体之间海明距离的方法来完成相近模型的排挤，保持种群的活力，见公式(7)。在每次计算之后，将适应度值较大的前N/k(k为排挤因子)个个体保存下来，与下一次计算得到的N个个体进行比较，对于海明距离小于设定值L的个体，根据适应度，施以一个较小的适应度值作为惩罚，增大它在下一次进化中淘汰的概率。通过使用小生境技术，可以预防个体过早陷于局部收敛，在某一范围内震荡的问题。

(7)

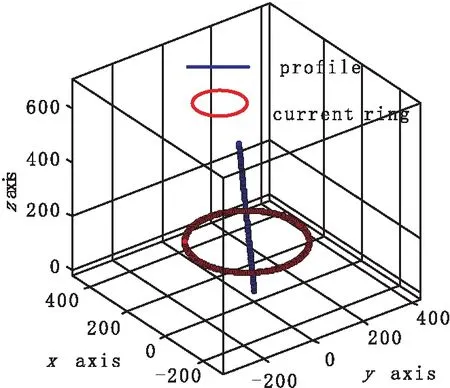
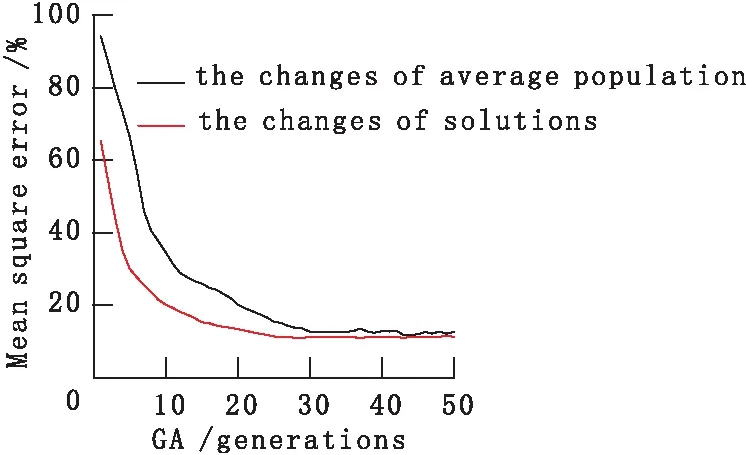
其中：i=1、2、3…M；j=(i+1，M-1)。当|ai-aj|

Fmin(ai,aj)=Fenalty

(8)

这样适应度小的个体，在下一轮进化中，淘汰的几率大大增加，通过多次循环，在局部范围内，适应度小的个体就被排除在外，有效避免了局部收敛问题。

在运用缩小收缩范围和小生境技术的同时，有条件地将最佳值复制到群体中，以解决“早熟、局部收敛”，以及“搜索迟钝”等问题。每代进化中，比较当前最佳值与上一代最佳值，若当前最佳值差，应将上一代最佳值复制到群体中，若当前最佳值好，不复制当前值，以防止未成熟收敛。

3 实验及结果展示

确定了使用缩小收缩范围和小生境相结合的改进型遗传算法之后，编制了基于等效涡流正反演程序，下面分别对井孔位于电流环外和电流环内两种情况下的空间响应(对应于地-井TEM的井中和井旁异常两种情况)进行反演试算并与传统遗传算法进行比较。反演结果使用相对均方误差进行衡量，其公式为：

(9)

其中：i=1、2、3…N,N为测点个数；Oi为第i个观测场值；Ti为第i个计算场值；P为方差。设定场值拟合均方误差小于等于1‰即达到计算精度要求，计算完毕。

1)模型1电流环半径为200 m，电流强度为0.3 A，电流环倾角为15°，旋转角为15°，电流环中心坐标为(350，400，150)，测线不通过电流环。其测线与电流环的空间位置如图3所示。

图3 测线与电流环的相对位置(环外)Fig．3 Opposite position of profile and current ring(off hole)

2)模型2。电流环半径为200 m，电流强度为0.3 A，电流环倾角为15°，旋转角为15°，为不失一般性，电流环中心坐标选为(35，90，150)，测线通过电流环。其测线与电流环的空间位置如图4所示。

图4 测线与电流环的相对位置(环内)Fig．4 Opposite position of profile and current ring(in hole)

反演初始模型如下：种群规模：4 000，种群参数为7，初始参数的范围如表1所示。

表1 遗传算法初始参数表

从图5、图7可以看出，对于传统遗传算法，遗传代数在25代左右解基本稳定，算法很快陷于局部收敛， 不能跳出，均方误差在10%以上；而对于改进型遗传算法(图6、图8)，解一直往最小值(最优方向)靠近，与传统遗传算法相比，遗传代数为25代左右时，均方误差已经小于5%，遗传50代时，遗传算法已经达到最优解(设定均方误差为1‰)。从图5至图8比较可以看出，改进型遗传算法能有效改善传统遗传算法易于陷入局部收敛的缺陷。

从表2、表3可以看出，使用传统的遗传算法，反演模型与理论模型误差巨大，这是因为在很宽泛的搜索空间中，存在无数个局部极值点，计算一旦陷入其中即进入死胡同无法跳出，得到的局部最优解与真解相差甚远。而使用了基于缩小收缩空间和小生境技术相结合的改进型遗传算法在经过少数几次搜索之后就能锁定最佳模型参数，获得精度很高的解，井孔位于电流环外时反演模型平均误差均为3.58‰，井孔位于电流环内时反演模型平均误差更是小到0.05‰。

图5 传统遗传算法种群均值和解的变化(环外)Fig．5 Variations of average population and solution by tradition GA(off hole)

图6 改进型传统遗传算法种群均值和解的变化(环外)Fig．6 Variations of average population and solution by improvement GA(off hole)

图7 传统遗传算法种群均值和解的变化(环内)Fig．7 Variations of average population and solution by tradition GA(in hole)

图8 改进型传统遗传算法种群均值和解的变化(环内)Fig．8 Variations of average population and solution by improvement GA(in hole)

4 结论

经过理论模型验证可以看出，使用基于缩小搜索空间和小生境相结合的混合遗传算法对简化为电流环的地-井TEM理论模型数据试算效果良好，反演模型差很小，这种混合遗传算法能够很好地抑制多参数多极值函数的早熟和局部收敛问题，使我们能够在有效搜索空间内获得较满意的解。

参考文献：

[1] BOTELHO, MARCO A B, PAUL L. STOFFA. Finite-difference reverse time migration of multi-configuration marine seismic data, 2nd international congress of the SBGf, salvador[J]. Brazil, Expanded Abstracts, 1991(11)：953-959.

[2] MALCOLM SAM BRIDGE. Genetic algorithms in seismic waveform inversion[J]. Geophysics , 1992,44 ：323-342.

[3] 陶春辉, 何樵登, 王晓春.用遗传算法反演层状弹性介质[J]. 石油地球物理勘探,1994，29(2)：156-165.

[4] 张厚柱, 杨慧珠, 徐秉业.用遗传算法反演层速度[J]. 石油地球物理勘探,1995，30(5)：633-644.

[5] BOSCHETTI F, DENTITH M, LIST R.Inversion of seismic refraction data using Genetic Algorithms[J]. Geophysics, 1996,(17):1715-1727.

[6] WILSON W G, LAIDLAW W G. VASUDEVAN K. Residual statics estimation using the genetic algorithm[J]. Geophysics, 1994, 59: 766-774.

[7] FABIO BOSCHETTI, RON D. L. Inversion of seismic refraction data using genetic algorithms[J]. Geophysics, November-december,1996,61(6): 1715-1727.

[8] 王兴泰, 李晓芹, 孙仁国.电测深曲线的遗传算法反演[J]. 地球物理学报,1996 (02): 342-352.

[9] 罗润林, 张小路.电阻率测深数据的遗传算法和最小二乘法反演[J]. 桂林工学院学报.19898，24(2)：152-254.

[10] 师学明, 王家映, 张胜业, 等. 多尺度逐次逼近遗传算法反演大地电磁资料[J].地球物理学报，2000(1)：122-130.

[11] 谭永基, 王金莲. 用遗传算法计算几个地球物理反问题[J]. 工程数学学报, 2005(3)：22-27.

[12] 谢维,柳建新. 混合遗传算法在大地电磁一维反演中的应用[J]. 物探化探计算技术,2009,31(6):156-159.

[13] 何伟兵, 刘江平, 杨明, 等. 小生境遗传算法及其在地球物理反演中的应用研究[J]. 工程地球物理学报, 2007,4(1):15-20.

[14] BARNETT C T. Simple inversion of time-domain electromagnetic data[J].Geophysics, 1984,49:925-933.

[15] FULLAGAR P K.Inversion of Down-hole TEM data using circular current filaments[J]. Exploration Geophysics,1987, 18:872-888.

[16] NABIGHIAN M N.Quasi-static transient response of a conducting half-space- An approximate representation[J], Geophysics,1979, 44:1700-1705.

[17] KEATING P B,CROSSLEY D J. The inversion of time-domain airborne electromagnetic data using the plate model [J], Geophysics, 1990，55:705-711.

[18] 米萨克 N. 纳比吉安. 勘查地球物理电磁法第一卷理论[M].赵经祥译,北京：地质出版社，1992.