地-井瞬变电磁井旁板状导体异常响应特征分析

张 杰，王兴春，邓晓红，吕国印，武军杰，杨 毅

(中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000)

0 引言

地-井瞬变电磁法(TEM)测量是将发射回线布置在井孔上方或附近地表，用接收探头在钻孔中测量地下介质产生的感应二次场，方法原理如图1所示[1-2]。在不接地回线中供以双极性脉冲电流，产生激发电磁场，在一次电磁场的激励下，地下介质受感应产生涡旋电流，当发射的脉冲电流从峰值跃变到零，激发场立即消失，而地下介质中的感应涡流并不立即消失，只是有一个衰变过程，这个过程的特征与地下电性结构分布有关。通过研究井中感应二次场在空间和时间上的变化特征，可以达到研究钻孔周围电性分布结构的目的，从而可以发现井旁、井底盲矿，或推断已见矿体的空间分布与延伸方向。

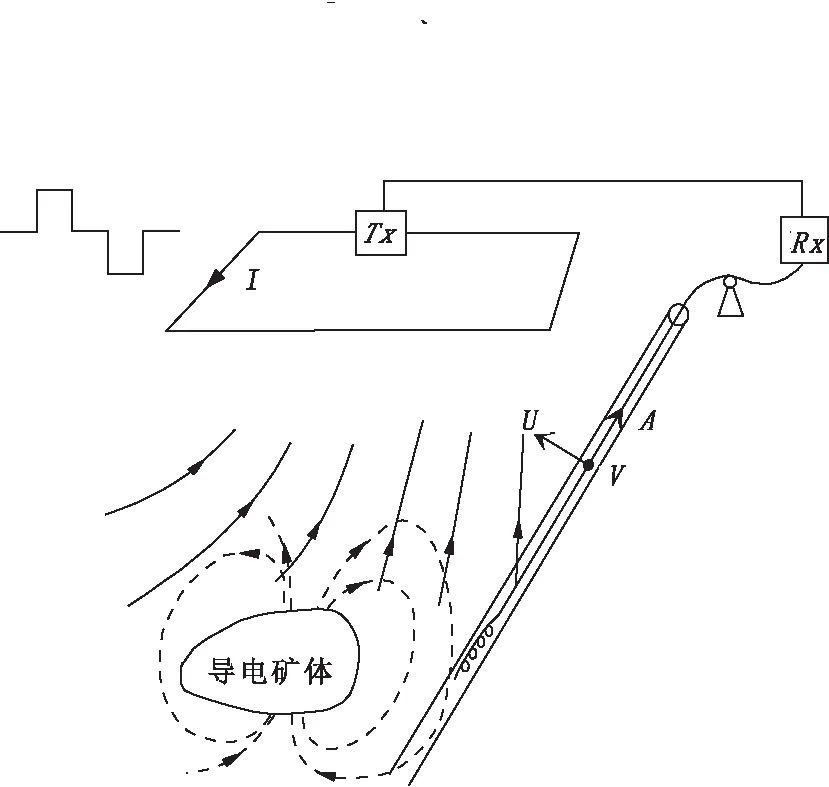
图1 地-井TEM法工作原理示意图Fig．1 Schematic diagram for surface to borehole TEM

空间中的一次、二次场都是矢量场，分析、研究地-井TEM响应曲线时必须先明确坐标系。按照加拿大CORNE公司地-井TEM系统的坐标系规定如下[3]：井轴分量A沿指向上为正，井经分量U、V按右手定则规定正方向，当钻孔为直孔时，即为笛卡尔右手坐标系，如图2所示，并规定发射电流方向以保证发射回线中心的一次场Z分量向上为前准。

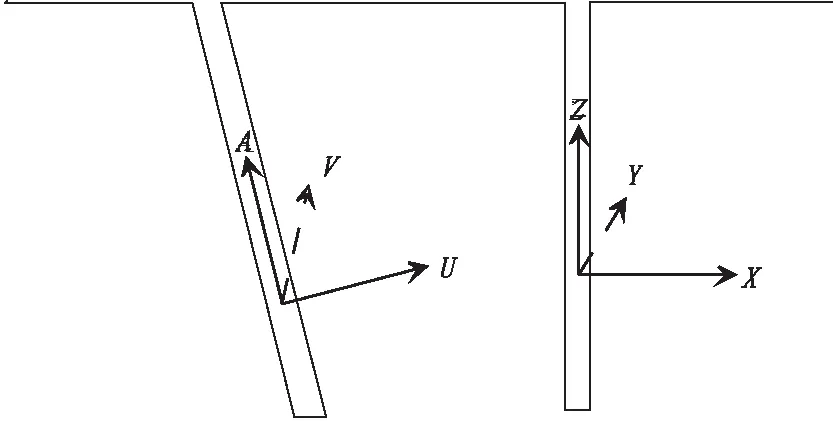
图2 地-井TEM坐标系Fig．2 Surface to borehole TEM coordinate system

地-井瞬变电磁法观测的异常响应值不仅与矿体的导电性和几何形态有关，还与发射回线、导体、接收探头之间的位置关系密切相关，且感应二次场属于矢量场，响应曲线的形态特征非常复杂，了解和认识典型异常响应曲线是地-井瞬变电磁资料解释的基础。作者利用商业化的EMVISION软件对井旁板状导体模型进行了数值模拟，获取了典型响应曲线，分析研究了井旁导电薄板响应曲线特征，总结了异常规律，为井旁盲矿异常的定性定量解释提供了依据。

1 地-井瞬变电磁典型异常特征

1.1 静态特征

静态特征指响应幅值随着接收探头位置(深度)的变化特征，图3展示了发射回线位于导体正上方时的四种Z分量响应典型特征，其中钻孔A穿过导体中部，为正异常特征；钻孔B穿过导体边部，异常特征为在正异常中出现反向异常；钻孔C穿过导电矿体外部附近，为强而陡的负异常特征；钻孔D穿过导电矿体远处，异常特征为弱而缓的负异常。

图3 地-井TEM响应静态特征曲线[2]Fig．3 Surface to borehole TEM's static characteristic curve

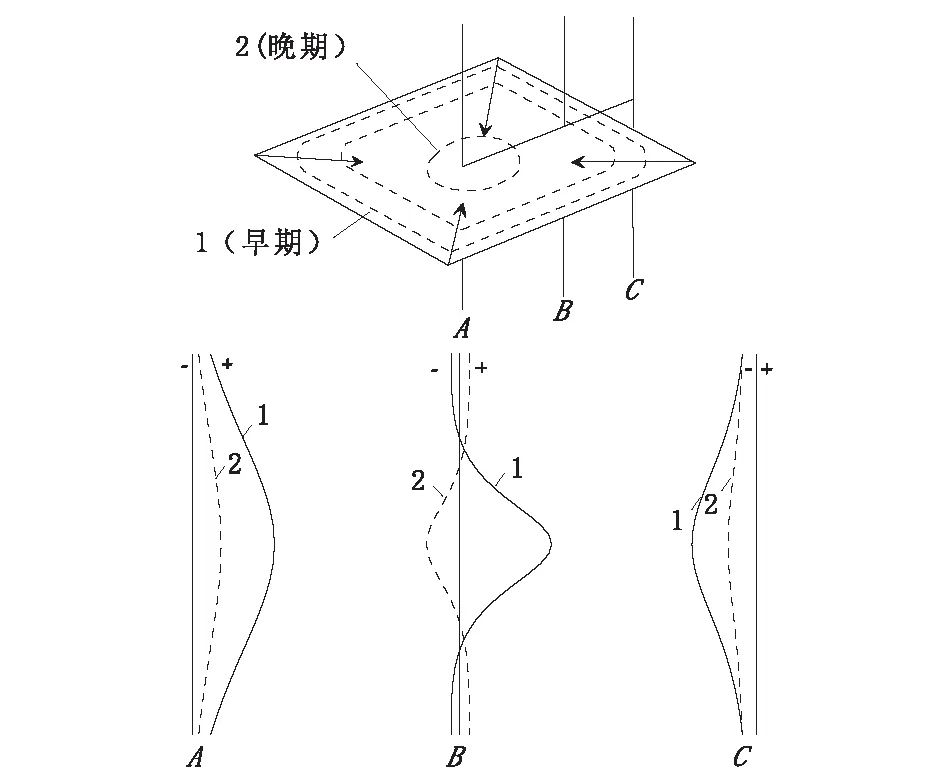
图4 地-井TEM响应动态特征曲线[2]Fig．4 Surface to borehole TEM's dynamic characteristic curve

1.2 动态特征

动态特征(或称时间特征)是指响应曲线的形状及特征点(如极值、过零点等)随采样延时的变化特征[4]，反映导体中感应涡流随时间的衰变及扩散规律，通常分为早、中、晚期，如图4所示，在穿过矿体中部的A孔中，观测到始终为正的响应值；在穿过矿体边缘的B孔中，将观测到中心由正变负、而两侧由负变正的响应值；位于矿体外侧的C孔中，将观测到始终为负的响应。

1.3 等效水平电流环响应特征

Dyck等[5]、Eadie等[6]描述了导体内感应涡流的建立与消失过程，导体内的电流分布可以用等效电流环表示。设边长为30 m×30 m的水平等效电流环，在不同位置设置取样钻孔，绘制剖面曲线(Z分量向上为正，X分量向右为正)。由于主剖面上Y分量响应幅值为零，且X与Y分量特征具有相似性，所以只需讨论X与Z分量。

A、B两孔穿过电流环内部，距电流环中心10 m，X、Z分量曲线如图5所示。两孔Z分量曲线完全一致，均为单峰正异常，极大值点与电流环深度对应。两孔X分量曲线形态完全相反，A孔位于电流环中心右侧，曲线显示为反“S”型，在电流环上部，幅值先由弱变强，达到极大值后又逐渐变弱，在电流环深度位置(Z=0)处出现“过零点”；在下部，幅值变为负值，且有一极小值。B孔位于电流环中心左侧，曲线为典型的“S”型。

图5 电流环内X、Z分量剖面曲线图Fig．5 X and Z components profile curve inside current-carrying loop

C钻孔、D钻孔、E钻孔、F钻孔都位于电流环外部，在x轴上的坐标位置分别为-50 m、-80 m、-110 m和-140 m，曲线如图6所示。由图6可见，在不同位置的X及Z分量曲线形态相似，幅值不同，X分量曲线显示为“S”型，Z分量曲线显示为单峰负异常。由图可见，Z分量极小值点位置与电流环深度一致，曲线都有“过零点”，且“过零点”均位于同一直线上(图6中绿线)，该直线与水平夹角约为θ=37.72°。利用θ角为一常数特征可以获取异常体的定量信息，以D孔为例，曲线“过零点”M与极值点N的距离|MN|可以从对应孔深上获得，钻孔与导体中心距离|NO|是需要推断的未知参数，由图6可见，|MN|/|NO|=tg(θ)≈0.8 为一常数，所以|NO|≈1.25|MN|，由于O点位于导体内部，则|NO|大于钻孔与导体边缘之间的距离r，因此，可以近似地推断r≈|MN|，即钻孔与导体之间的距离约为Z分量异常宽度的一半。

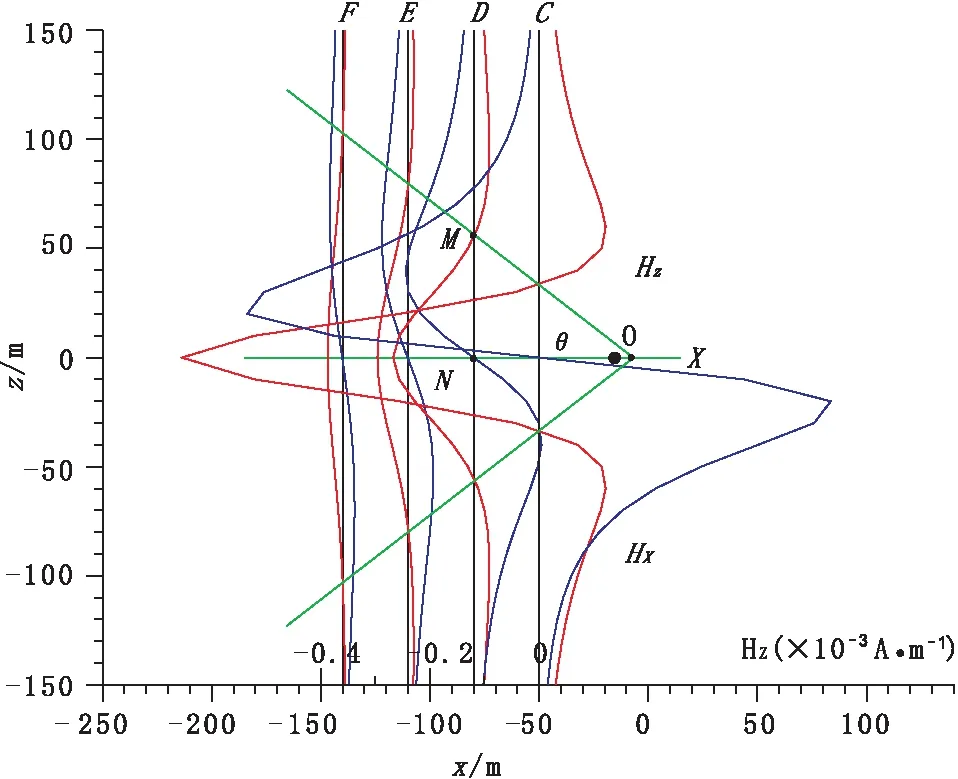
图6 电流环外X、Z分量剖面曲线图Fig．6 X and Z components profile curve outside current-carrying loop

2 井旁板状导体异常响应特征

2.1 板体与钻孔位置关系变化的曲线特征

Dyck等[5]在物理和数值模拟结果的基础上，对利用地-井瞬变电磁三分量测量解决目标体位置、产状和埋深等问题的可能性进行了探讨，指出同时在井中观测三个正交分量将有助于解决解释中的多解性问题。

为了研究钻孔与导体之间位置关系对响应曲线的影响规律，采用EMVISION软件进行数值模拟，设计模型为：自由空间内嵌入一个200 m×200 m的水平薄板，电导率为50 S，深度为200 m。在与板体中心重合的300 m×300 m正方形四边均匀地设置A—P十六个垂直钻孔，孔深400 m。发射回线位于板体正上方，边长400 m×400 m，发射电流为1 A，接受线圈等效面积1 000 m2，采样延迟时间见表1。模型示意图及数值模拟得到各个钻孔的三分量响应曲线如图7所示。

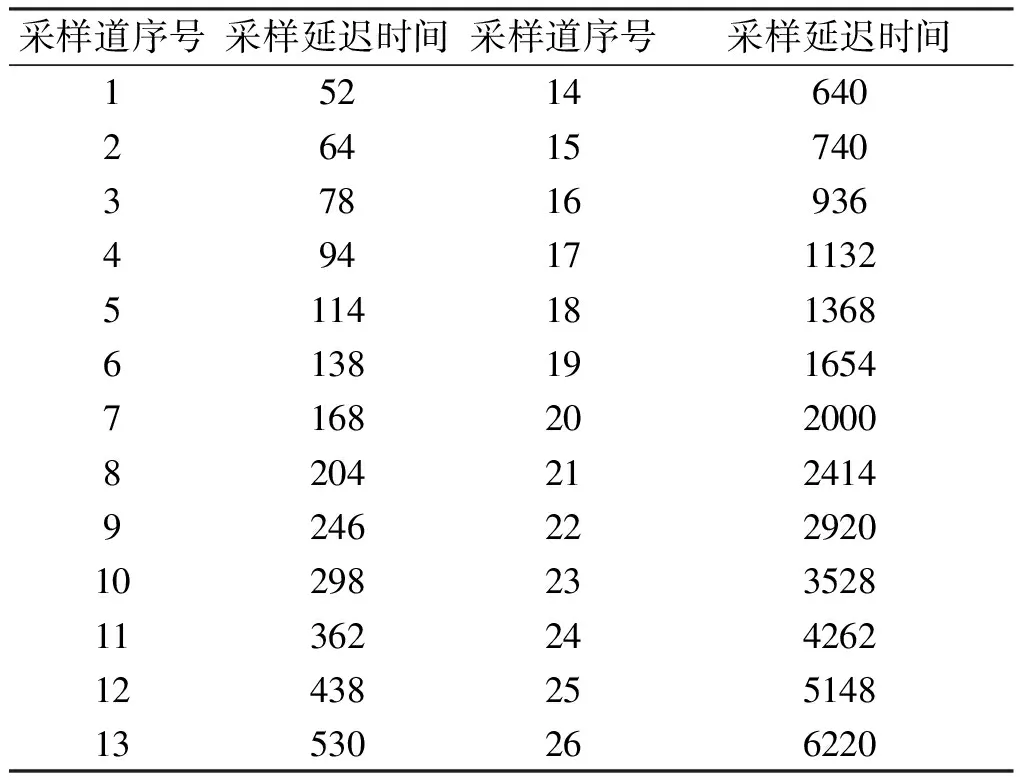
表1 取样延迟时间表Tab.1 Sampling schedule 单位：μs

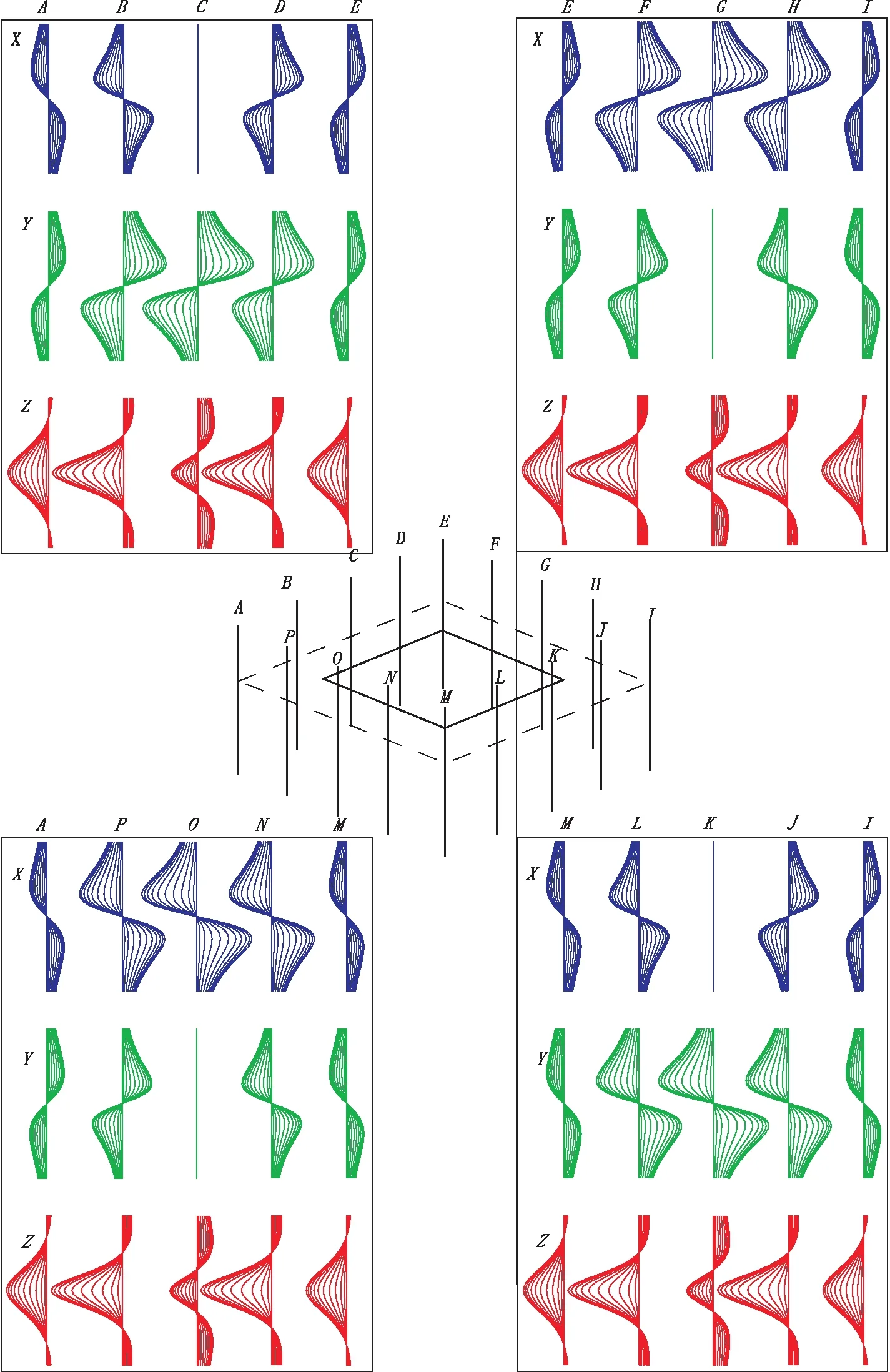
图7 板体与钻孔不同位置关系响应剖面曲线图Fig．7 Profile for plate and borehole's relative position

由响应曲线可见，Z分量响应曲线特征完全一致，均为单峰负异常，而且在与板体中心相对称的钻孔中，响应幅值均相同，如A、E、I和M孔相同；B、D、F、H、J、L、N和P孔相同，所以通过Z分量曲线只能确定板体的深度而不能确定其方位。由图7可见，16个钻孔的三分量曲线没有完全相同的，A孔X曲线为“S”型、Y曲线为反“S”型；E孔X、Y曲线均为反“S”型；I孔X曲线为反“S”型、Y曲线为“S”型；M孔X、Y曲线均为“S”型。经过分析可以总结出如下特征规律：以钻孔为坐标原点，若板体中心位于某水平方向(X或Y)的正方向一侧，则观测到该水平方向分量的响应曲线为“S”型；反之，则响应曲线为反“S”型。

所以通过分析水平分量响应曲线，可以推断异常中心的大致方位，方法总结如下：以钻孔为原点，X、Y轴将水平面划分为四个象限，若X、Y分量曲线为“S”型，则导体中心位于第一象限(L、M、N)；若X分量为反“S”型，Y分量为“S”型，则导体中心位于第二象限(H、I、J)；若X、Y分量曲线为反“S”型，则导体中心位于第三象限(D、E、F)；若X分量为“S”型，Y分量为反“S”型，则导体中心位于第四象限(A、B、P)，如图8所示。而且通过对比X与Y分量响应幅值可以判断导体中心的偏向，若Y分量幅值较大，则导体中心离Y轴较近，当导体中心正位于Y轴时，Y分量响应幅值达到最大而X分量响应为零，如C、K孔；若X分量幅值较大，则导体中心离X轴较近，当导体中心正位于X轴时，X分量幅值达到最大而Y分量响应为零，如O、G孔。

2.2 板体倾角变化的响应特征

数值模拟条件为：回线边长400 m×400 m，钻孔位于回线中心，孔深为600 m，，发射电流为1 A，下降沿0.2 ms，接收线圈等效面积为1 000 m2，取样延迟时间见表1。模型参数为：自由空间内嵌入一个200 m×200 m的薄板，电导率为20 S，顶边埋深为300 m、距钻孔为250 m；板体中心点在水平面上的投影位于X轴上(图9)。板体与水平面的夹角为板体的倾角dip(下倾为正，上倾为负)，分别计算不同倾角情况下井中TEM响应。

由图10可见，虽然发射回线与钻孔的位置不变，但板体倾角改变除了使其中心产生位移，还使穿过板体的磁力线发生变化。由于板体上感应涡流的磁矩总是垂直于板面，所以不同倾角板体上感应涡流的磁矩方向，与板体倾角及一次场穿过板体方向有关。

图11、图12是数值模拟的剖面曲线，由于板体中心位于X轴，且板体为X轴对称的规则体，Y分量响应均为“0”值，因而只需绘制X和Z分量响应曲线。

图11是下倾板体的剖面曲线图，倾角分别为0°、15°、30°、45°、60°和90°。当板体水平时，Z分量曲线为单峰负异常，极小值点深度就是板体中心深度；X分量曲线显示为反“S”型，曲线过零点深度为板体中心深度。当下倾15°时，板体中心向下移动，Z分量曲线的极下值点向下移动，响应幅值变化不明显，异常宽度(上下过零点的距离)明显加大，曲线远端的正响应有明显的变化，上端增强而下端减弱；X分量曲线的过零点也向下位移，上端的正异常响应增强，下端的负异常响应减弱。当倾角逐渐增大，上述曲线变化的规律进一步明显，尤其当倾角增至45°时，Z分量下端正响应曲线全部变为负值，使曲线形态由单峰向反“S”型过渡；同样，X分量曲线形态也由反“S”型向单峰转变。当倾角增大至90°时，Z分量曲线为反“S”型，曲线过零点深度就是板体中心深度，X分量曲线为单峰正异常，极大值点的位置就是板体中心深度。

图8 X、Y分量曲线特征与异常中心位置分布关系图

图9 板体倾角为0°时平面投影图Fig．9 Plane projection for plate (dip=0°)

图10 不同倾角板体及一次场分布图Fig．10 Plate with different dip and primary field distribution

图11 下倾板体响应剖面曲线图Fig．11 Profile for descend plate

图12 上倾板体响应剖面曲线图Fig．12 Profile for updip plate

图12是上倾板体的剖面曲线图，倾角分别为0°、-15°、-30°、-45°、-60°和-90°。当上倾-15°时，板体中心向上移动，Z分量的极小值点向上移动，异常宽度增大，曲线上端正响应减弱下端增强；X分量曲线的过零点向上位移，曲线上端正响应减弱，下端负响应增强。当倾角逐渐增大，曲线变化的规律进一步明显。当上倾-45°时，X、Z分量响应幅值已减弱至最小，且Z分量曲线变为“S”型，X分量曲线变为单峰形态。当倾角增大至-60°时，X、Z分量曲线均出现了“反转”现象，即与上倾-45°时相比，相同位置的响应值产生了变号，Z分量曲线由“S”型变为反“S”型，X分量曲线由单峰负异常变为单峰正异常。通过分析图10可以较容易理解曲线反转现象，由图10可见，板体倾角在-45°～90°范围内，一次场磁力线均由板体底部进入顶部穿出，而在倾角为-60°～-90°时，穿过板体的一次场磁力线由顶部进入而由底部穿出，所以板体内二次感应涡流的磁矩方向发生“反转”，二次场反向。

2.3 板体埋深变化的曲线特征

数值模拟条件为：回线边长400 m×400 m，钻孔位于回线中心，孔深为600 m，发射电流为1 A，下降沿0.2 ms，接收线圈等效面积为1 000 m2。模型参数为：自由空间内嵌入一个 200 m×200 m的薄板，电导率为20 S，倾角为45°，板体中心在水平面上的投影位于(200，0，0)，板体中心埋深ho分别设为100 m、150 m、200 m、250 m、300 m和400 m六种情况，图13为不同埋深板体与一次场分布断面图。

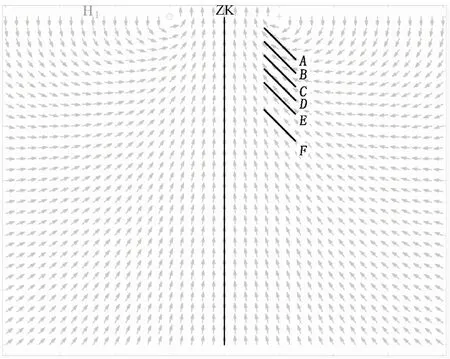
图13 不同埋深板体及一次场分布图Fig．13 Plate with different depth and primary field distribution

图14是数值模拟得到的井中TEM响应剖面曲线，由于板体关于X轴对称，Y分量的响应值均为“0”，因此，图中只绘制了X、Z分量响应曲线。由图13可以直观地看出，当板体埋深较浅(50 m)时，板体中心附近一次场以较大交角从上向下穿过板体，X分量曲线显示为较强的单峰负异常，Z分量曲线显示为板顶深度位置为正响应，板尾深度位置为负响应。当埋深增大时，响应曲线的特征点随板体中心向下位移，且响应幅值也逐渐减弱，当增大至200 m时，由图13可见，在此位置附近一次场近乎与板面平行，对板体的激发处于较差状态，响应曲线在同一比例尺下已变的很弱。埋深继续增大为250 m、300 m和400 m时，一次场穿过板体的方向变为由下向上，得到的TEM响应曲线随之“反转”，如图14所示。

图14 不同埋深板体地-井TEM响应剖面曲线图Fig．14 Surface-borehole TEM profile for plate with different depth

2.4 板体与钻孔距离变化的曲线特征

数值模拟条件为：回线边长400 m×400 m，钻孔位于回线中心，孔深为600 m，发射电流为1 A，下降沿0.2 ms，接收线圈等效面积为1 000 m2。模型参数为：自由空间内嵌入一个200 m×200 m的薄板，电导率为20 S，倾角为45°，板体中心埋深为300 m，设计了六种板体与钻孔不同距离的情况，如图15所示，数值模拟曲线如图16所示。

图15 不同水平位置板体及一次场分布图Fig．15 Plate with different horizontal position and primary field distribution

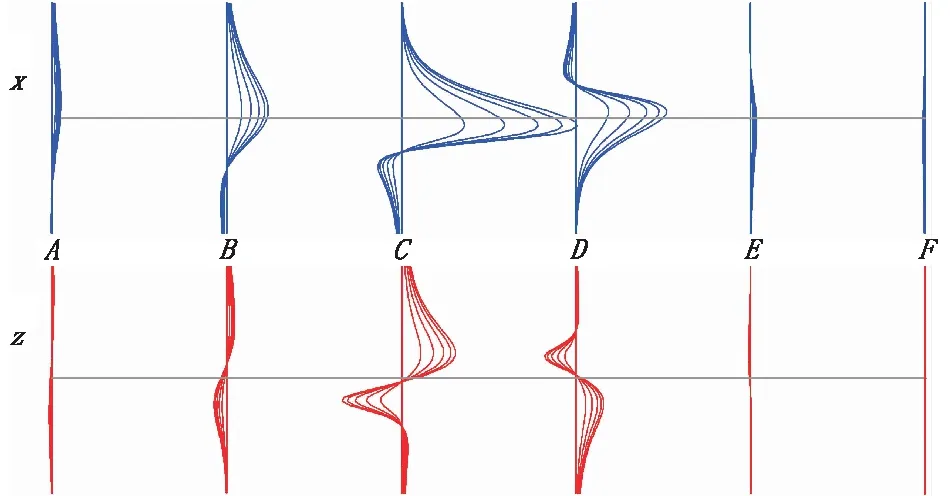
图16 不同埋深板体地-井TEM响应剖面曲线图Fig．16 Surface-borehole TEM profile for plate with different depth

由图15、图16可见，A→B→C位置板体中心与钻孔的距离逐渐减小，由下向上穿过板体的一次场方向与板面交角增大，响应曲线幅值增强、异常范围变窄、形态特征不变。当板体位于D位置时，虽然板体中心离钻孔距离与C处相同，但由于板体倾斜，使其与一次场的耦合关系没有C位置有利，所以响应幅值比C处弱，且Z分量响应曲线“反转”。当板体位于E时，一次场方向与板面交角进一步减小，响应曲线幅值在同一比例尺下已接近零轴。当板体位于F时，由图15可见一次场穿过板体的方向变为由上部向下穿过，响应值的符号再次“反转”，由于响应强度较弱，使图16中(E)→(F)曲线的符号变化无法分辨，只要将横坐标比例尺增大就可以清晰地看出曲线的符号变化。

3 结论

地-井瞬变电磁响应特征与多种因素相关，曲线形态变化复杂，我们通过等效电流环和数值模拟，讨论了简单条件下井旁板状导体的曲线特征，并总结了一些规律和方法，取得了主要认识和结论：

1)地-井瞬变电磁场属于矢量场，研究表明：在相同的发射、接收条件下，地-井TEM三分量异常响应特征与异常体位置关系具有一一对应的高度相关性，在实际工作中同时观测三个分量将有助于井旁异常位置的推断解释。

2)通过分析水平分量异常响应曲线的特征和幅值，可以推断异常中心的大致方位，若曲线为“S”型，则异常中心位于该分量的正方向一侧；若曲线为反“S”型，则位于该分量的负方向一侧。

3)垂直分量异常响应曲线能反映异常中心与钻孔之间的距离，钻孔穿过异常中部，垂直分量异常曲线为正异常；穿过异常体边缘，早期道反映为正异常，中晚期道变为负异常；井旁异常曲线为负异常特征，且异常半宽度约等于异常体与钻孔的距离。

4)地-井瞬变电磁响应特征非常复杂，通过分析一次场与导体之间的耦合关系能够清晰地了解响应特征变化的根源，所以利用一次场分布图有助于对复杂模型的推断解释。

参考文献：

[1] 蒋邦远. 实用近区磁源瞬变电磁法勘探[M].北京：地质出版社，1998.

[2] 牛之琏. 时间域电磁法原理[M].长沙：中南大学出版社，2007.

[3] CRONE． Geophysics &Exploration Ltd[M]. R.A.D Tool Operation, 2003.

[4] MICHAEL W.Asten Alan King and Johnn Peacock, Sign Changes in DHEM Surveys for Cindered Coal in the Sydney Basin[J]. Exploration Geophysics, 1987(18)：319-323.

[5] DYCK A V,WEST G F.The role of simple computer models in interpretation of wide-band, drill-hole electromagnetic surveys in mineral exploration[J]. Geophysics, 1984,49：957-980.

[6] EADIE T，STALTARI G. Introduction to Downhole Electromagnetic Methods[J].Exploration Geophysics,1987(18)：247-254.