超空泡航行体纵向平面动力学行为的CFD分析

于开平，张 广，邹 望，李振旺

（哈尔滨工业大学 航天学院，哈尔滨 150001）

超空泡航行体纵向平面动力学行为的CFD分析

于开平，张 广，邹 望，李振旺

（哈尔滨工业大学 航天学院，哈尔滨 150001）

超空泡航行体稳定性及弹道特性的仿真研究是设计超空泡航行体控制和制导系统的基础。文章基于多相流URANS（Unsteady Reynolds Averaged Navier-Stokes）方程和刚体纵向平面运动学方程，建立了三维超空泡航行体动力学仿真模型，对纵向平面内超空泡航行体巡航状态的动力学行为进行了仿真研究。仿真结果表明，超空泡航行体在无控条件下仍具有一定的稳定性；尾部控制面可以有效缩短航行体达到稳定所需要的时间，并且能使航行体稳定于空泡中心构成理想的稳定模式。

流体力学；超空泡航行体；动力学行为；CFD

1 引 言

超空泡技术为大幅提高水下航行体速度带来了光明的前景，但是由于超空泡航行体系统本身的复杂性，使得该项技术在实际的应用中面临着诸多挑战，其中超空泡航行体的稳定性和控制问题尤为突出[1-2]。

近些年来，国内外学者基于表征空泡形态的数学模型[3-4]，通过相应模型的简化和假设，构建了系列超空泡航行体的动力学模型并探讨了相关控制方法。所研究的问题涉及单自由度模型，三自由度模型和六自由度模型。Kirschner[5]和Kulkarni[6]基于简单的单自由度模型，研究了无控超空泡射弹的动力学行为，得到了航行体水平航行的一些典型特征参数。

文献[7-8]考虑了空泡的记忆效应以及航行体尾部滑行的非线性作用，建立了超空泡航行体非线性动力学模型。Goel[9]对一个有固定空泡外形的六自由度航行体进行了研究，对模型进行了基于小扰动的线性化后分析了稳定性，得到了纵向和横向无控运动的稳定性结论。从以上的研究工作来看，在超空泡航行体动力学建模过程中，空泡形态和相应的流体动力项主要采用经典的势流理论经验公式构建，对模型进行了不同程度的线性化处理，这样导致的结果是难以精确预测航行体与空泡之间复杂的相互作用，影响数值计算精度。

随着计算机水平的不断提高，计算流体动力学（CFD）方法已经成为预测和揭示一些复杂流动现象的有效手段。本文在文献[10-12]工作的基础上，通过对商用CFD软件CFX进行二次开发，耦合多相流URANS方程和刚体纵向平面运动学方程，结合动网格技术，建立了三维超空泡航行体纵向平面数值计算模型。数值模型综合考虑了航行体和航行体控制面与空泡表面复杂的非线性力作用，空泡形态的三维瞬态特性及湍流影响，对超空泡航行体巡航阶段的动力学行为及弹道特性进行数值研究。

2 数值计算模型

2.1 基本控制方程

本文研究自然空泡流动问题，采用均质平衡流模型，假设汽水两相具有相同的速度场和压力场，两相之间不存在相对速度。

连续性方程：

动量方程：

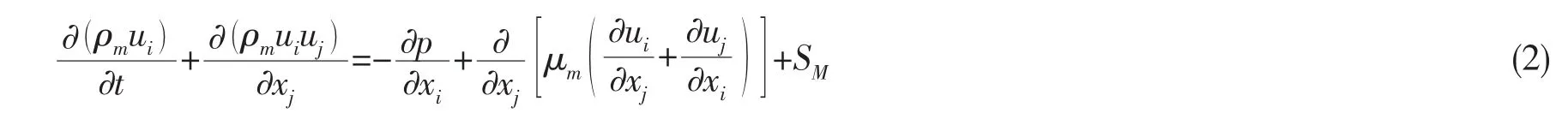
其中：ρm，μm分别为按体积分数确定的混合物的密度和动力粘度，u为速度，SM为源项。

2.2 湍流模型［10］

针对本文所涉及的问题，在稳态数值仿真中使用SST（Shear Stress Transport）湍流模型，而非稳态仿真采用能够精确预测湍流影响的LES模型，分别简要介绍如下：

基于Baseline（BSL）k-ω模型的SST湍流模型解决了湍流剪切应力的传输问题，同时又对逆压梯度下产生的分离流具有较高精度的预测，基本方程如下：

其中：ρ为密度、U为速度矢量、Pk表示湍流的生产率，其它参量的具体表达式本文不再赘述。

LES（Large Eddy Simulations）模型的基本思想是认为湍流流场是由不同尺度的涡旋组成，通过滤波函数把流场瞬时变量分为大尺度涡运动和小尺度涡运动。大尺度涡通过直接求解瞬态N-S方程模拟，不直接模拟小尺度涡，小尺度涡对大尺度涡的影响采用亚格子模型（Subgrid-scale model）进行模拟。

大涡的运动基本方程：

在LES方法中通过使用滤波函数，对于任意流场变量φ可以划分为两个部分，即滤波后的大尺度平均分量和通过亚格子模型表示的小尺度分量φ′，滤波后的变量可以通过下式得到：

其中：V表示流动区域，x为滤波后大尺度空间上的空间坐标，y为实际流动区域中的空间坐标，G(x,y ）为滤波器函数且满足：

假设滤波过程和求导过程可以交换，用滤波函数处理瞬时N-S方程和连续方程得到：

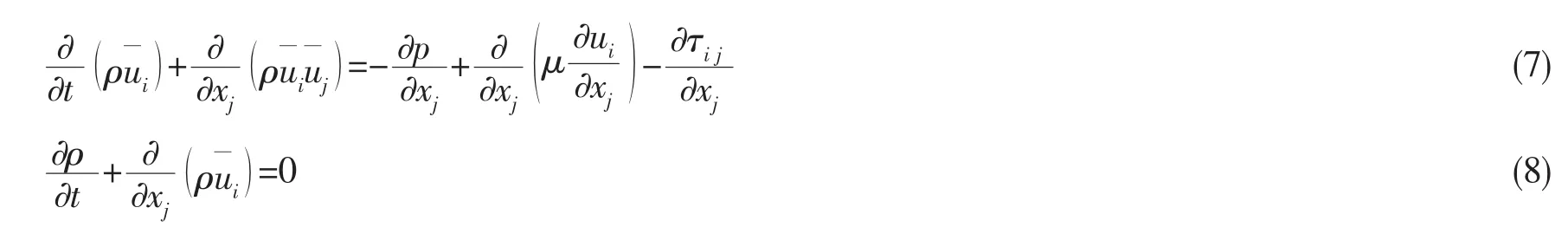
2.3 空化模型[10]

忽略热传输和非平衡相变效应，空化流动中蒸汽相体积分数输运方程为：

本文采用Rayleigh-Plesset气泡动力学方程来描述液体中气泡的生长和溃灭过程，上式源项可分别表示为：

式中：pv为气泡内压力，p 为环境压力，αv是蒸汽的体积分数，rnuc是成核点体积分数，RB=1×10-6m，rnuc=5×10-4，Fe=50，Fc=0.01。

2.4 纵向平面刚体运动学方程

选取地面坐标系OXYZ并建立原点位于航行体质心的弹体坐标系oxyz来描述超空泡航行体运动规律，如图1所示。本文假定航行体为质量恒定的刚体，建立在航行体质心的纵向平面运动学方程组如下：

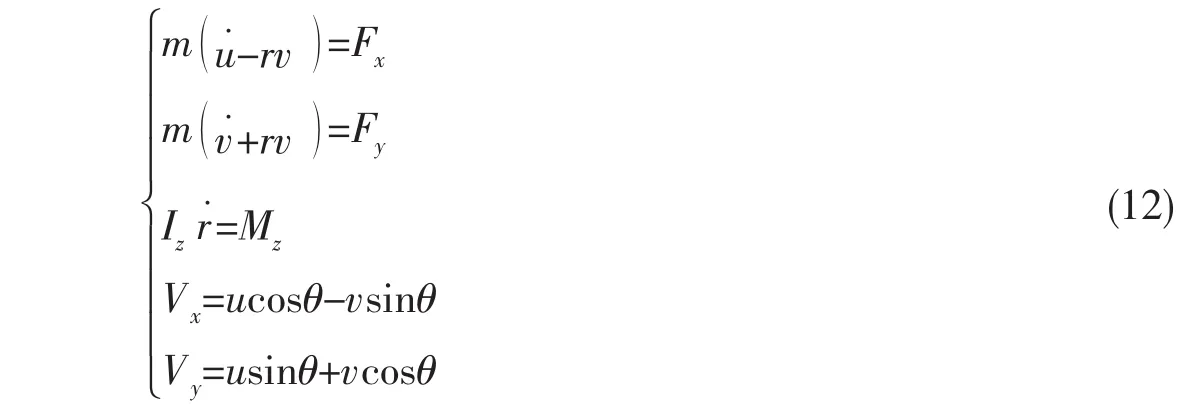
图1 坐标系示意图Fig.1 The sketch map of reference frame

式中：m为航行体质量，u，v为航行体速度在体坐标系x，y方向上的分量，r为航行体系绕z轴的角速度，Fx，Fy为航行体所受合外力在体坐标系x，y方向上的分量，Iz，Mz分别为航行体相对z轴的转动惯量和合外力力矩，Vx，Vy为航行体在地面坐标系下的速度分量，θ为航行体俯仰角。为了研究巡航段航行体运动规律，进一步假定航行体推力能够保证航行体维持x方向速度恒定。以上运动方程经过时间离散化后利用CFX内部的CEL语言嵌入数值计算模型。

3 仿真模型及边界条件设置

数值模拟采用两种超空泡航行体模型，模型布局参考文献[13]，如图2所示。航行体主要由头部圆盘空化器、锥柱段弹身、楔形尾翼和尾喷管组成。尾翼的作用类似于常规水下航行体的十字形舵控制面，尾翼穿透空泡与流体相互作用而产生用于平衡航行体重力的升力及转动力矩。两种模型的基本参数详见表1。计算域及边界条件设置如图3所示，整个计算域均采用六面体结构化网格离散，网格单元总数为1 121 500，如图4所示。

图2 计算模型Fig.2 Computation models

图3 计算域及边界条件Fig.3 Computational region and boundary conditions

表1 航行体模型基本参数Tab.1 Vehicle model parameters

计算域的进口和出口分别定义为速度入口和压力出口，外边界采用速度入口条件。本文建立的数值模型将相对运动原理和非惯性坐标系动力学方程相互结合。针对航行体纵向平面的两个平动自由度采用相对运动原理进行处理，平动速度及加速度的变化通过运动学方程计算后施加到相应进口边界。而对与航行体姿态的变化则完全采用动量矩方程控制动网格运动求解，通过这样的设置可以大大缩减完全使用动网格进行数值求解的计算量。

图4 航行体模型计算网格Fig.4 Computational grids around vehicle model

图5 稳态仿真计算结果Fig.5 Steady-state simulation results

4 计算结果与讨论

首先，通过调整流场参数得到能够覆盖整个航行体的超空泡稳态解，将其作为纵向平面弹道模拟的初始解。图4给出了水深H=5 m、航行体水平速度V0=100 m/s，自然空化数σv=0.024条件下的稳态初始解。这里自然空化数定义为：σv=2（ P∞- Pv）/ρV20，其中P∞为环境压力、Pv=3 170 Pa为25℃水的饱和蒸汽压力、ρ为水的密度。

图6给出了超空泡航行体模型1各项参数的无控弹道仿真结果，仿真时间为T=1 s，时间步长 Δt=0.001 s。 图 6（a），图 6（b）分别为航行体垂向速度和深度的变化曲线。由于超空泡航行体被气相介质包络基本丧失浮力作用，初始阶段在重力的作用产生了垂直向下的速度分量，航行体小幅下沉，但持续时间较短。航行体下沉导致其尾部表面与空泡下表面发生碰撞，产生沾湿区，在来流的高速冲击作用下，沾湿区域产生“滑行力”的作用。在初始阶段尾部滑行力随着垂向速度的减小迅速增大，在垂向速度达到最小值的同时滑行力也达到峰值，如图6（d）所示，可见航行体垂向速度对空泡尾部滑行力即沾湿区域的变化影响显著。

受尾部滑行力的作用航行体垂向速度方向迅速改变并进一步增加，最后逐渐稳定在Vy=4 ms。整个仿真过程中航行体向上爬升约3.5 m。图6（c）给出航行体俯仰角的变化曲线，可以看到航行体姿态不断变化，俯仰角在仿真过程前期持续增大而后逐渐稳定于θ≈3.44°。各项仿真参数变化在t=0.6 s左右均趋于稳定，航行体最后处于稳定滑行状态如图7所示。这同文献[14]所指出的超空泡尾部滑行稳定状态相同，可见无尾翼的超空泡航行体在无控条件下依然可以保持一定的稳定性。

图8给出了带尾翼超空泡航行体模型2的无控弹道仿真结果。可以明显发现模型2的仿真结果与模型1呈现较大差异，尾翼对超空泡航行体的弹道特性产生显著影响。由于航行体自身重力、尾部控制面升力及俯仰力矩的作用，航行体从一开始便逐渐下沉且垂向速度不断减小，航行体的姿态由初始的水平直航状态逐渐过渡到以俯仰角θ≈-2.86°的下潜状态。模型2仿真的最终结果如图9所示，航行体完全位于空泡内部中心位置，没有出现类似于模型1的尾部滑行状态。可见由于航行体尾部控制面所产生的升力代替了模型1中的滑行力作用从而构成了超空泡航行体比较理想的稳定航行方式。

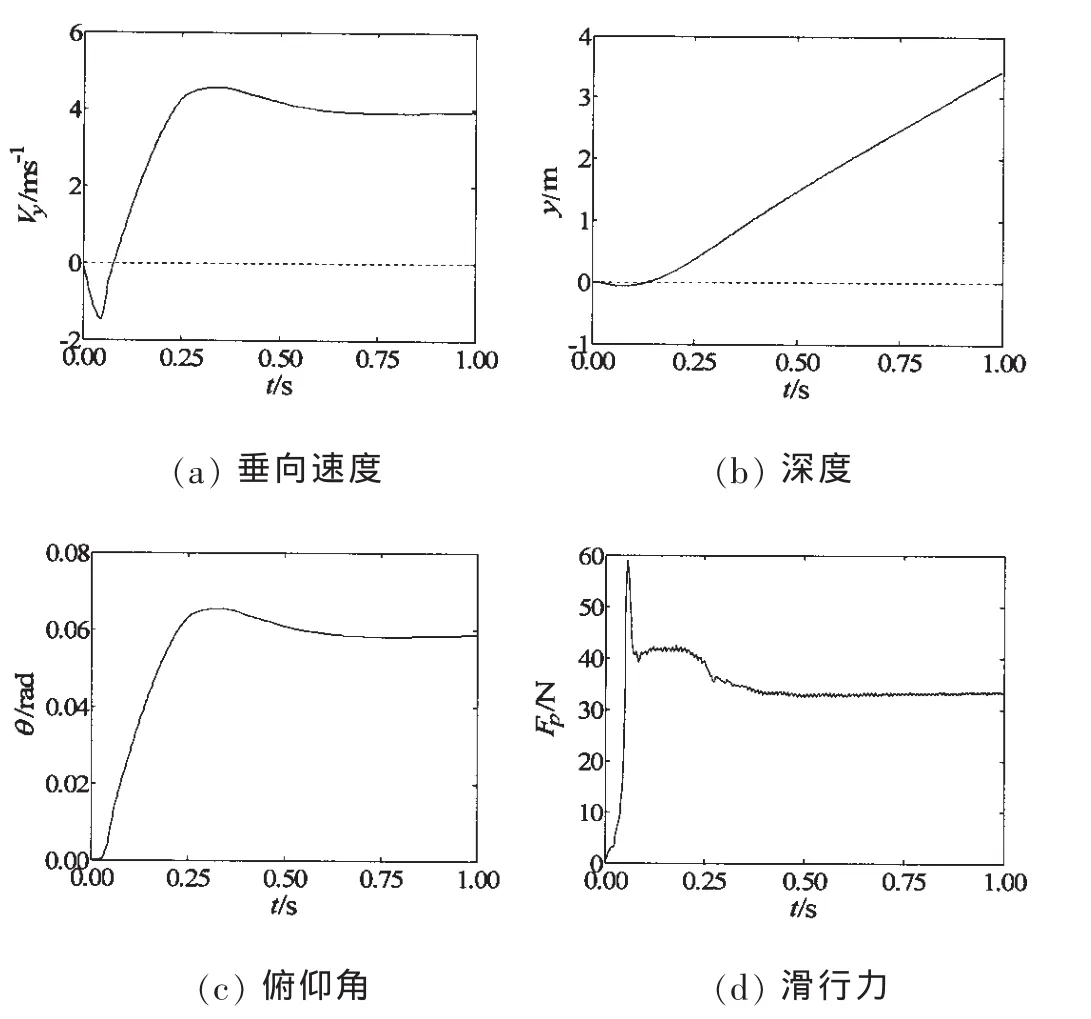
图6 航行体模1无控弹道仿真结果Fig.6 The simulation results of uncontrolled trajectory of model 1

图7 航行体模型1尾部滑行模式Fig.7 Planing model of vehicle model-1

图8 模型2无控弹道仿真结果及模型阻力变化曲线Fig.8 The simulation results of uncontrolled trajectory of model 2 and resistance curves

对比图6和图8，航行体从初始状态到稳定状态各项参数变化的历程可以发现，具有尾部控制面的航行体能够更平稳、更快地达到稳定航行状态。所不足的是尾翼的存在大大增加了航行体的流动阻力，从图8（d）可见模型2的阻力约为模型1阻力的1.52倍，这就意味着需要消耗更多的推进能量来维持带有尾翼控制面航行体的稳定巡航状态。

图9 航行体模型2的稳定状态Fig.9 Steady state of model 2

5 结 论

本文耦合计算了多相流体URANS方程和刚体运动学方程，结合动网格技术建立了三维超空泡航行体纵向平面无控弹道数值模型。针对两种不同的航行体模型进行了无控弹道仿真，分析了超空泡航行体纵向平面的动力学行为，得到的主要结论如下：

（1）垂直于航行体轴向的速度分量导会致空泡尾部偏移变形进而对尾部滑行力产生显著影响。

（2）在无控条件下超空泡航行体仍具有一定的运动稳定性，本文通过CFD仿真得到了Savchenko所提出的超空泡航行体尾部滑行稳定运动方式。

（3）尾部控制面可以有效缩短航行体达到稳定所需要的时间，并且能使航行体稳定于空泡中心构成理想的稳定模式。

本文建立的数值模型为纵向平面超空泡航行体弹道仿真提供了相应的数值研究手段，据此可进一步开展大量的数值模拟研究，系统的研究超空泡航行体弹道变化规律及各种外在因素对弹道特性的影响。

[1]David R Stinebring,Robert B Cook,John E Dzielski,Robert F Kunz.High-speed supercavitating vehicles[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Colorado,August 2006.

[2]Kirschner I N,Kring D C,Stokes A W,Fine N E,Uhlman J S.Control strategies for supercavitating vehicles[J].Journal of Vibration and Control,2002,8(2):219-242.

[3]Reichardt H.The laws of cavitation bubbles as axially symmetrical bodies in a flow[R].Ministry of Aircraft Productuin(Great Britian),Reports and Translations,1946(766):322-326.

[4]Vasin A D.The principle of independence of the cavity sections expansionas the basis for investigation on cavitation flows[Z].VKI Special Course on Supercavitating Flows,Brussels:RTO-AVT and VKI,2001:RTO-EN-010(8).

[5]Kulkarni S,Pratap R.Studies on dynamics of a supercavitating projectile[J].Applied Mathematical Modeling,2000,24(2):113-129.

[6]Kirschner I N,Ulman J S.Simplified dynamical system analysis of supercavitating high-speed bodies[C]//In Fifth International Symposium on Cavitation(CAV2003).Osaka,Japan,2003.

[7]Geol A.Robust control of supercavitating vehicles in the presence of dynamic and uncertain cavity[D].Florida:University Of Florida,2005.

[8]王京华,魏英杰,于开平,王 聪,黄文虎,吕 瑞.基于空泡记忆效应的水下超空泡航行体建模与控制[J].振动与冲击,2010,29(8):160-163.

[9]Vanek B,Bokor J,Balas G J,Arndt R E.Longitudinal motion control of a high-speed supercavitation vehicle[J].Journal of Vibration and Control,2007,13(2):159-184.

[10]周景军,于开平.空化器倾斜角对超空泡流影响的三维数值仿真研究[J].船舶力学,2011,15(1):74-80.

Zhou Jingjun,Yu Kaiping.Three dimensional numerical simulation on the influence of cavitator inclination angle to supercavity flow[J].Journal of Ship Mechanics,2011,15(1):74-80.

[11]Yu Kaiping,Zhou Jingjun,Min Jingxin,Zhang Guang.A contribution to study on the lift of ventilated supercavitating vehicle with low Froude number[J].Journal of Fluids Engineering,2010,132:111303-1～111303-7.

[12]Zhou Jingjun,Yu Kaiping,Zhang Guang.Research on the process of supercavity development and the evaluation on two methods of studying the planing state[J].Journal of Ship Mechanics,2011,15(3):200-206.

[13]Pan Zhancheng,Lu Chuanjing,Chen Ying,Hu Shiliang.Numerical study of periodically forced-pitching of a supercavitating vehicle[C]//9th International Conference on Hydrodynamics.Shanghai,China,2010:856-861.

[14]Savchenko Y N.Control of supercavitating flow and stability of supercavitating motion of bodies[R].RTO AVT lecture series on supercavitating flows,Von Karman Institute,Brussels Belgium,2001:12-16.

CFD analysis of the dynamic behavior of supercavitating vehicle in the longitudinal plane

YU Kai-ping,ZHANG Guang,ZOU Wang,LI Zhen-wang

(School of Astronautics,Harbin Institute of Technology,Harbin 150001,China)

Numerical simulation research on the stability of supercavitating vehicle and trajectory is the basis of designing control and guidance system of supercavitating vehicle.In this paper,based on the multiphase flow URANS(Unsteady Reynolds Averaged Navier-Stokes)equations and the kinematical equation of the rigid body in the longitudinal plane,the three-dimensional dynamics simulation model of supercavitating vehicle is established.On this basis,the dynamic behavior of supercavitating vehicle is simulated in the cruising state.The results show that the supercavitating vehicle without control may still be stable to some extent,and fins can effectively decrease the time which the vehicles take to be stable and make the vehicle locate in supercavity as a stable motion mode.

hydromechanics;supercavitating vehicle;dynamic behavior;CFD

U661.2+2 TV131.2

A

10.3969/j.issn.1007-7294.2014.04.003

1007-7294（2014）04-0370-07

2013-11-10

国家自然科学基金重点项目（10832007）

于开平（1968-），男，哈尔滨工业大学航天学院教授，博士生导师；

张 广（1983-），男，哈尔滨工业大学航天学院博士研究生，Email:zhangguang925@163.com。