内倾船型的瘫船倾覆特性研究

王田华，顾 民，鲁 江，张进丰

（中国船舶科学研究中心 水动力学重点实验室，江苏 无锡214082）

内倾船型的瘫船倾覆特性研究

王田华，顾 民，鲁 江，张进丰

（中国船舶科学研究中心 水动力学重点实验室，江苏 无锡214082）

文章采用非线性时域方法进行内倾船型在横浪中横摇运动的数值预报，并在计算中考虑了船体瞬时湿表面变化对水动力的影响。在此基础上，通过对波浪时域历程下船舶的整个倾覆过程进行模拟计算，建立了船舶在瘫船状态下的倾覆概率计算方法。在耐波性水池进行了内倾船型在瘫船状态下的大幅极限运动模型试验，采用模型测试数据对计算结果进行了验证。对内倾船型在波浪中的倾覆特性进行了研究，得到不同海况下的倾覆概率和倾覆前的平均时间，并给出了内倾船型GM的建议取值。

瘫船稳性；内倾船型；横浪；倾覆概率

1 引 言

近年来，内倾船型由于其良好隐身性能而被各国广泛关注，其船型特点为低干舷、折角线以上内倾设计和穿浪型舰艏[1-2]，这些非传统船型特点使得其稳性性能和常规船型差别很大，其内倾设计导致船体倾斜时恢复力矩较常规船型明显减少，尤其是大倾角时的恢复力矩，而且内倾船型甲板上浪严重，有时整个艏部会埋入波浪中，引起较大的稳性损失[3]。因此，在高海况条件下，内倾船型的倾覆危险会明显大于常规船型，稳性问题已成为制约内倾船型在水面舰船上应用的关键。此外，国际海事组织（IMO）目前正在制定关于瘫船稳性的薄弱性衡准，作为非传统船型的内倾船因船型特点可能会导致其在波浪中稳性失效而倾覆，受到IMO薄弱性衡准研究的关注。对于内倾船型，采用常规的稳性计算方法已无法对其在波浪中的稳性进行有效的计算和评估[4]，采用先进的力学理论和概率方法对其在波浪中的倾覆特性进行计算与研究已成为其稳性研究和评估的一个主要技术手段[5]。

船舶在随机海浪上的倾覆过程是一个极其复杂的力学问题，到目前为止，人们仍然对倾覆现象缺乏完整的数学描述和准确的数值模拟手段。时域仿真是分析船舶在随机海浪中的稳性原理的一个简明的方法，可以灵活地处理复杂的非线性水动力问题。本文针对内倾船型的水动力特点和横摇倾覆特性，采用基于切片理论的非线性时域计算方法，考虑瞬时湿表面变化对恢复力和入射力的影响，辐射力和绕射力用平均吃水作计算，对内倾船型在横浪规则波和不规则波中的横摇运动，尤其是大幅横摇运动，进行了数值计算，并通过模型试验进行了验证。在此基础上，通过对波浪时域历程下船舶的整个倾覆过程进行模拟计算，建立了船舶在瘫船状态下的倾覆概率计算方法。对内倾船型在波浪中瘫船状态下的倾覆特性进行了研究，重点研究不同海况和GM值对内倾船型的影响规律。

目前，处理船舶大幅度运动的非线性因素主要是基于切片理论的时域修正方法，在一定程度上计入非线性影响，具体做法是入射力和恢复力考虑瞬时湿表面积变化，而辐射力和绕射力用平均吃水作简化计算，这在常规直壁船舶预报上有一定的效果[6]，但对于内倾船型的适用性还有待研究。本文对内倾船型在横浪规则波和不规则波中的横摇运动，尤其是大幅横摇运动，进行了数值计算和试验研究，数值计算中采用了非线性时域方法，并考虑了瞬时湿表面的变化，通过数值计算结果和试验数据的对比分析，研究了内倾船型大幅横摇运动的非线性特点和在横浪中的倾覆特性。

2 船舶倾覆概率数值预报技术

2.1 船舶大幅极限运动模拟

为了在计算横摇运动时可以考虑其它运动模式的影响，采用船舶在波浪中的六自由度运动时域[7]方程：

其中： j=1,2,…,6 分别表示纵荡、横荡、升沉、横摇、纵摇和首摇，ηk表示位移或转动角度，η˙k表示速度，η¨k表示角速度，mjk是船舶本身惯性力系数；Cjk是静水恢复力系数矩阵，波浪力Fj（）t为入射力与绕射力之和，Ajk和Bjk分别是附加质量和阻尼系数矩阵。

船舶横摇阻尼是准确预报横摇运动的关键，具体地，船舶横摇阻尼系数为：

其中：ajk和bjk为采用切片理论求得的剖面附加质量和阻尼系数，U为航速；可以采用经验公式计算粘性横摇阻尼，较常用的是Ikeda基于模型试验提出的半经验公式，把非线性横摇阻尼写成等效线性化的形式。为了提高计算精度，在条件具备的情况下，可以采用模型试验得到的阻尼系数。

在进行非线性水动力修正时，由于恢复力和入射力是水动力的主要部分，要考虑瞬时湿表面积变化做精确计算：

其中：FS+FK为恢复力和傅汝德—克雷洛夫力之和；SB（）t为船舶瞬时湿表面，具体计算时，采用入射波对应的瞬时湿表面，不考虑绕射波和辐射波影响；ps和pFK分别为静水压力和入射波压力，由于入射波对应的瞬时波高在剖面上有正有负，也就是入射波波面有时在静水面上，有时在静水面下，故静水压力计算至入射波波面 τ，即 ps=-ρgz，-∞＜z＜τ；而入射波压力为：

其中：z≤0 时，z1=z，而 z＞0，z1=0。

在船舶运动计算时，考虑到瞬时边值问题求解的复杂性，本文采用下述方法作处理，预先在频域里计算一系列有初始横倾、纵倾和升沉状态的水动力系数（包括附加质量和阻尼、入射力、绕射力），建立水动力系数关于初始横倾、纵倾和升沉状态的数据库文件；时域计算中，根据每一时刻船舶的横倾、纵倾和升沉，在数据库中线性插值求得船舶当前姿态的水动力系数；最后根据当前船舶姿态的水动力系数，代入运动方程（1），给定初值，即可计算出船舶运动时历。

2.2 船舶倾覆概率计算原理

船舶在运动过程中，倾覆是一个非常小的概率事件[8]，倾覆概率可通过在数值计算中遭遇倾覆的频率来计算，即蒙特—卡洛方法：

其中：NC是Nr个记录中出现倾覆的数量，假定每个记录都是相同时长Tr（本文数值预报时长为半小时），当样本容量足够大时，其置信区间为（假定服从正态分布）：

其中：半宽Kβ可以通过标准差表示，对于概率为95%时的可接受的置信度，Kβ=1.959 96；同样，倾覆前的平均时间Tc也可以通过倾覆概率和其置信区间的边界值Tcu,cl来计算：

置信区间的上下边界为：

3 瘫船稳性及倾覆试验研究

通过对内倾船瘫船状态下在横浪规则波和不规则波中的极限运动模型试验，得到其在横浪中的横摇运动响应，验证船舶运动计算方法对模拟内倾船横摇运动计算的有效性。

试验模型主要尺度见表1，图1为模型的船体型线图。模型试验在中国船舶科学研究中心耐波性水池中进行，采取定点试验模式，模型首尾两端通过四根弹簧绳约束，见图2，进行零航速横浪试验。通过静水中的船模自由横摇衰减试验，得到模型横摇固有周期Tm=1.468 s。对于规则波试验，波高一定时，取12～15个波长的规则波进行试验，其波长与船长比0.5～4，即波长约为1.5～15 m。为了研究大幅横摇运动规律，选取共振波长，即波浪周期等于横摇固有周期，波高选取不同的值。不规则波模型试验时，采用ITTC双参数波谱：

表1 内倾船模型参数Tab.1 Tumblehome form model characteristics

图1 内倾船船体型线图Fig.1 Body plan of tumblehome hull form model

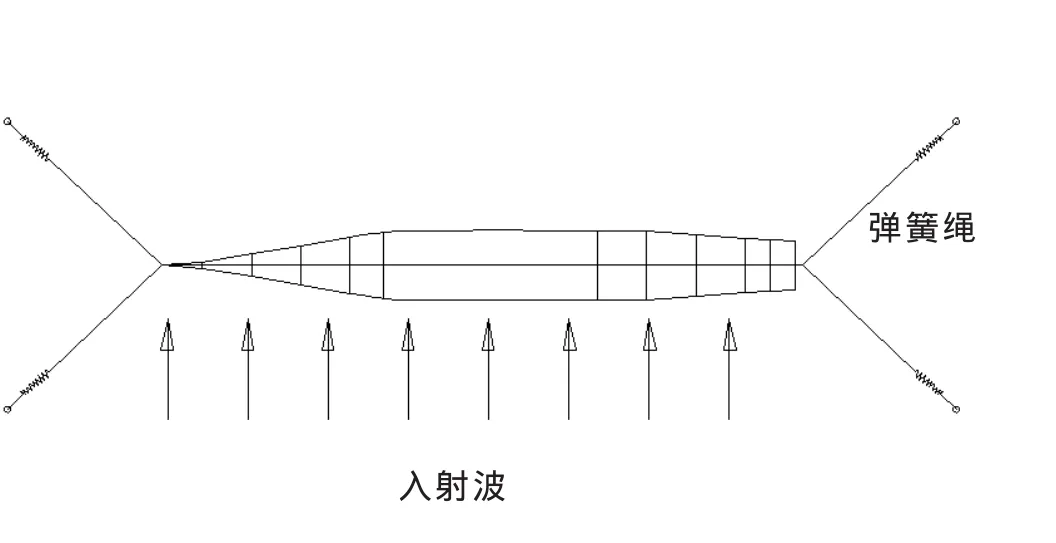
图2 模型试验约束模式Fig.2 Wire system with springs for test

4 船舶极限运动数值预报结果

4.1 极限运动与倾覆数值预报技术的验证

为了验证数值方法对内倾船型横摇运动计算的适用性，在自由漂浮状态，对内倾船型在横浪规则波和不规则波中的运动进行了横摇运动计算，下面将计算结果和模型试验结果进行了对比分析。

图3 横摇运动幅值函数与试验对比Fig.3 Comparison for the calculated roll responses and test data

图4 规则波中横摇幅值计算结果和试验对比Fig.4 Comparison for the calculated roll amplitudes and test data in regular waves

图3为非线性时域方法计算的横摇响应与试验的对比，图中横轴为波浪圆频率，纵轴为无因次横摇响应，可以看出，计算结果与试验值吻合良好，说明本文所采用的数值计算模型计算稳定，结果可靠。图4为波浪周期等于横摇固有周期即Tw=Tφ时，规则波中的横摇幅值与试验结果的对比，从图中可以看出，二者吻合较好，随着波高的增加曲线斜率逐渐减小，横摇运动和波高成非线性关系。

图5为采用非线性时域方法计算得到的不规则横浪中的波浪和横摇运动时历，表2为不规则横浪中数值计算的横摇振幅的有义值和最大值及其试验值，通过比较可以看出，采用时域理论计算的横摇振幅的有义值和最大值略大于试验值，误差在可接受范围之内，可认为该数值预报方法对内倾船型是有效的。

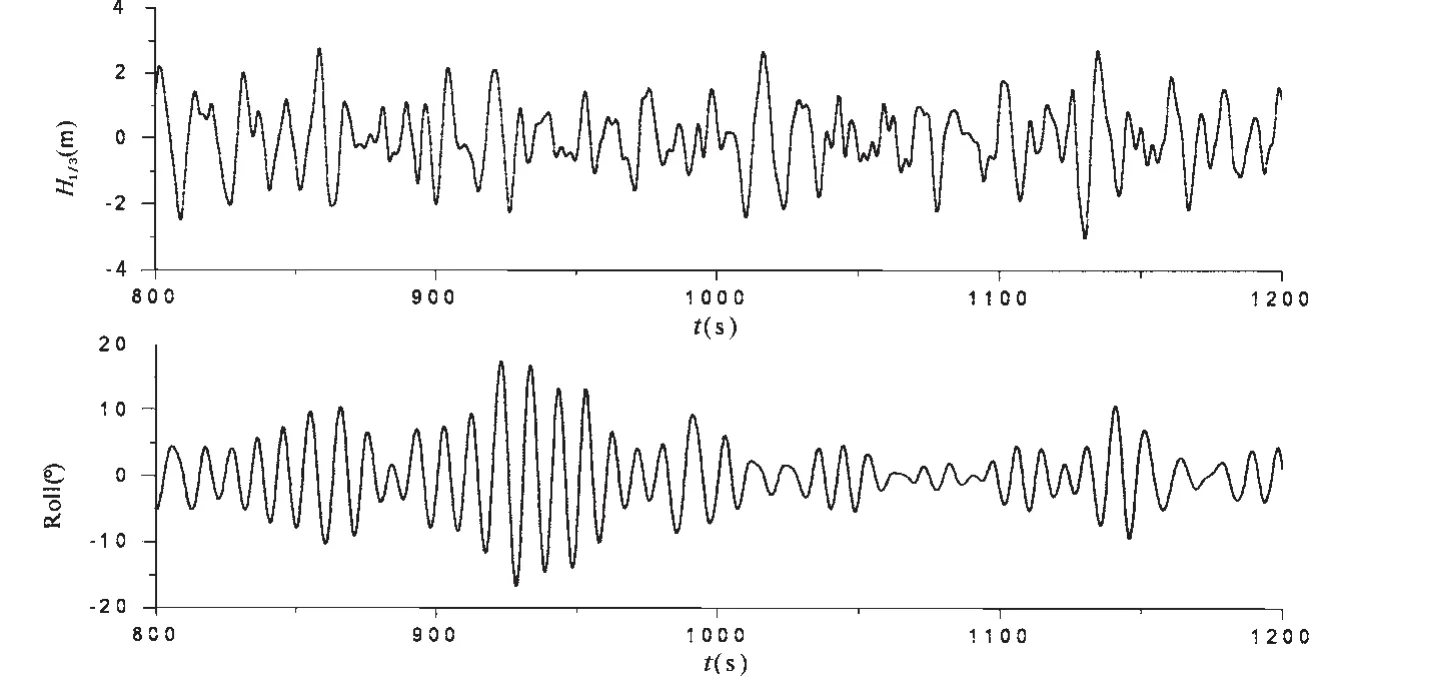
图5 不规则波横浪和横摇运动时历计算结果（H1/3=4.32 m，T01=8.31 s）Fig.5 Time histories of wave and roll motions in irregular waves(H1/3=4.32 m,T01=8.31 s)

表2 不规则波中横摇运动单幅有义值和最大值Tab.2 Significant single amplitudes and maximum of roll motion in irregular waves

4.2 内倾船型的极限运动及倾覆特性分析

由于船舶在随机海浪中的运动是随机的，且不同GM值时的稳性情况不一样，故船舶倾覆现象的发生也是随机的，对每个海况，采用多个时间历程计算足够的时间长度，数值模拟整个横摇过程和倾覆发生的过程。图6为该船在GM=1.5 m时发生倾覆的情况下横摇运动和横摇力矩的时历图，可看出在某一时刻横摇力矩急剧增大，导致横摇角也急剧增大，最终导致船体发生倾覆。

图6 倾覆时横摇和横摇力矩时历计算结果（GM=1.5 m，H1/3=9.95 m，T01=15.65 s）Fig.6 Time histories of roll motion and moment in irregular waves at capsizing state(GM=1.5 m,H1/3=9.95 m,T01=15.65 s)

针对不同海况、不同GM值时的船体倾覆过程进行模拟计算，将计算结果采用2.2小节中给出的方法进行统计分析，得到随机海况下的倾覆概率和倾覆前的平均时间，见表3。本文给出的内倾船型，当GM=1.0 m时，在7级海况下会发生瘫船状态下的倾覆，在有义波高为6.16 m时，倾覆概率达到0.56；当GM=1.5 m时，在8级海况下会发生瘫船倾覆，在有义波高为9.95 m时，倾覆概率达到0.15；当GM=2.0 m时，在9级海况中，瘫船状态下不发生倾覆。从上述的分析中可以看出，GM值对内倾船型的倾覆特性影响很大，在总体设计中必须重点考虑。

表3 内倾船倾覆概率计算结果Tab.3 Numerical results of capsizing probability

5 结论与建议

本文在采用非线性时域方法进行大幅横摇运动数值预报的基础上，建立了船舶在波浪中倾覆概率数值评估方法，通过模型试验和数值计算对内倾船型在波浪中的横摇运动和倾覆特性进行了研究，得出以下结论：

（1）本文采用的非线性时域方法模拟内倾船型在波浪中的大幅横摇运动与模型试验结果基本一致，表明该方法对内倾船型在瘫船状态下的大幅横摇运动模拟是有效的；

（2）本文建立的数值预报方法可以对船舶在瘫船状态下高海况中的整个倾覆过程进行时域模拟，以此为基础建立船舶倾覆概率数值预报技术可以对内倾船型在瘫船状态下的倾覆特性进行计算与评估；

（3）GM值对内倾船型的影响很大，在内倾船型的总体设计时必须重点考虑。从本文的计算结果看，为了避免船体倾覆发生，内倾船型的GM值应大于1.5 m。

本文采用船舶倾覆概率数值预报技术较好地模拟了船舶大幅横摇运动和倾覆过程，所建立的方法用于瘫船稳性分析是有效可行的。由于计算倾覆概率和倾覆前的平均时间要采用较多的样本数，而且对每个波浪历程都要对船舶的整个倾覆过程进行模拟，计算比较耗时，因此有必要开发快速而可靠的瘫船稳性计算方法，可以考虑根据波浪和横摇角幅值的概率分布进行倾覆概率统计计算，这是下一步需要研究的方向。

[1]张进丰,顾 民,魏建强.低干舷隐身船波浪中纵向运动的模型试验及理论研究[J].船舶力学,2009,13(2):169-176.Zhang Jinfeng,Gu Min,Wei Jianqiang.Model testing and theoretic study of the longitudinal motions in waves of low-freeboard stealthy ship[J].Journal of Ship Mechanics,2009,13(2):169-176.

[2]Olivieri A,Francescutto A,Campana E,Stern F.Experimental investigation of parametric roll in regular head waves for the ONR tumblehome[C]//28th Symposium on Naval Hydrodynamics.Pasadena,California,2010.

[3]Hashimoto H.Pure loss of stability of a tumblehome hull in following seas[C]//Proceeding of 19th International Offshore and Polar Engineering Conference.Osaka,Japan,2009.

[4]Hashimoto H,Umeda N,Sogawa Y,Matsuda A.Parametric roll of a tumblehome hull in head seas[C]//Proceeding of 19th International Offshore and Polar Engineering Conference.Osaka,Japan,2009.

[5]Japan.Draft direct assessment on stability under dead ship condition and its numerical validation[S].SLF53/INF.10,Annex7,IMO,2010.

[6]Fonseca N,Soares C G.Time-domain analysis of large-amplitude vertical motions and wave loads[J].Journal of Ship Research,1998(42):139-153.

[7]Fonseca N,Soares C G.Validation of a time-domain strip method to calculate the motions and loads on a fast monohull[J].Applied Ocean Research,2004(26):256-273.

[8]Belenky V,Weems K M,Lin Woei-Min.Numerical procedure for evaluation of capsizing probability with split time method[C]//27th Symposium on Naval Hydrodynamics.Seoul,Korea,2008.

Study on capsizing characteristic of a tumblehome hull under dead ship condition

WANG Tian-hua,GU Min,LU Jiang,ZHANG Jin-feng

(China Ship Scientific Research Center,Wuxi 214082,China)

In this research,the roll motion of tumblehome hull is forecasted numerically by a nonlinear time domain method considering hydrodynamic variation caused by the hull instaneous wet surface.The time histories of capsizing motion are simulated at time domain and the method of predicting capsizing probability under dead ship condition is established.Model test of the tumblehome hull for large amplitude motions under dead ship condition is carried out in the seakeeping basin and calculated results are verified by the model test data.The capsizing probability,the mean time before capsizing and the suggested GM value are obtained based on the investigation on the capsizing characteristic of the tumblehome hull.

stability under dead ship condition;tumblehome hull;beam sea;capsizing probability

U661.2+2

A

10.3969/j.issn.1007-7294.2014.04.002

1007-7294（2014）04-0363-07

2013-12-21

王田华（1986-），女，中国船舶科学研究中心工程师，E-mail:tianhua_wang@126.com；

顾 民（1962-），男，中国船舶科学研究中心研究员。