应用于数字下变频中CORDIC算法的FPGA实现

闫温合,胡永辉,李瑾琳,何在民,吴成英,赵坤娟



应用于数字下变频中CORDIC算法的FPGA实现

闫温合1,2,3,胡永辉1,2,李瑾琳4,何在民1,2,吴成英5,赵坤娟1,2,3

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院精密导航定位与定时技术重点实验室，西安 710600； 3. 中国科学院大学，北京 100049；4. 湖北省电力公司信息通信分公司，武汉 430077；5. 湖北民族学院，恩施 445000）

正余弦信号在GNSS接收终端的数字下变频中有着重要的应用，CORDIC算法是实现正余弦信号的最重要方法。立足于DDS与CORDIC算法的基本原理，针对CORDIC算法实现主要存在的3个问题，结合变象限法、流水线技术及相幅量化数据格式，在FPGA上通过实现CORDIC算法可在一个时钟周期内计算出正余弦信号幅值。仿真结果表明：与传统CORDIC算法实现相比，本文实现的正余弦信号精度高且速度快，并能满足GNSS接收终端数字下变频对正余弦信号的需求。

CORDIC算法；流水线结构；正余弦信号；数字下变频（DDS）

0 引言

在GNSS（global navigation satellite systems）接收终端中，数字下变频器（digital down-converter，DDC）主要实现的功能是将A/D采样后的数字信号从中频信号变成基带信号，它是用本地的同相载波和正交载波分别与接收中频信号相乘，这样可以剥离载波并在后续电路中差分解调时利用同相和正交2个分量消除相差的影响[1]。由于下变频混频器位于接收系统的前端，它的性能对整个接收系统的性能影响很大，所以需要快速和精准地进行正余弦函数的计算，传统的乘、除等计算方法在FPGA中实现时需要占用大量的片内资源，并且三角函数的运算很难实现。早期的硬件实现方法是采用查表法，多项式展开或近似的方法，这些方法在速度、精度、资源方面不能很好兼顾。CORDIC（the coordinate rotational digital computer）算法是J. E. Volder于1959年在美国航空控制系统的设计中提出的一种用于计算一些常用的基本运算函数和算术操作的循环迭代算法[2]。1971年J. S. Walther 提出改进的统一CORDIC算法[3]，他把圆周运算、双曲旋转和直线旋转统一到一个CORDIC迭代方程里，为统一的硬件实现提供了理论基础。该方法是用一系列与运算基数相关的角度不断偏摆从而逼近所需旋转的角度，从广义上讲它是一个数值性计算逼近的方法，由于这些固定的角度与计算基数有关，运算只有移位和加减。与传统的查表法相比，CORDIC实现节约了大量的ROM资源，可以满足GNSS接收终端数字下变频对正余弦信号产生精度和速度的需求。

1 CORDIC算法与传统的DDS基本原理

1.1 传统的DDS基本原理

直接数字频率合成技术（direct digital synthesis，DDS）是美国学者J. Tierney，C. M. Resder和B. Gold于1973年首先在论文《A Digital Frequency Synthesizer》中提出的。与其他的频率合成技术相比较，这种方法具有输出频率可调、频率切换时间短、输出相位连续、分辨率高、相对带宽宽和易于调制等许多优点[4]，传统的基于查表法的DDS典型结构如图1所示，由图1可见DDS主要包含以下单元：相位累加器、正弦查表RAM、D/A转换器以及一个低通滤波器。

图1 传统的DDS工作原理

传统的DDS实现简单，但是随着精度的提高，FPGA实现时RAM模块占用存储器单元呈指数增长，这不仅使设计对硬件资源的要求过高，而且降低了系统的处理速度，因而不能满足节省资源的要求。

1.2 CORDIC算法原理

图2 CORDIC算法原理示意图

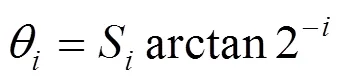
由式（7）可知，是一个增益因子，实现的时候可以单独处理，而无需每一次运算时都重新计算，具体的作法是将增益存储在ROM中，需要用到的时候查表即可，于是可以得到组合迭代方程为

于是经过次迭代之后，CORDIC输出变为

从以上的分析可以看出，CORDIC算法在圆周系统的旋转模式下可以用来计算一个输入角的正弦、余弦和正切。

2 CORDIC算法的FPGA实现

现场可编程逻辑器件（FPGA）是在专用集成电路（ASIC）的基础上发展起来的一种新型逻辑器件，其特点是用户可以完全通过软件进行配置和编程，完成某特定的功能，并且它可以反复擦写[6]。在本设计中选用的FPGA芯片是Altera公司开发的CyclonII系列中的EP2C70F896C6器件，使用Verilog语言完成电路描述，在QuartusII11.1软件平台上进行编译，仿真部分使用Model公司的硬件仿真工具Modelsim6.5b。

CORDIC算法的FPGA设计主要存在3个问题[7]。1）旋转角度覆盖范围为

因此只能达到[-99.88°，+99.88°]，无法覆盖整个周期；2）CORDIC算法在一次角度运算中必须使用多次迭代，而每次迭代方向都必须根据上一次迭代的结果确定，即每次迭代必须在上次完成以后进行，从而导致速度减慢；3）数据格式问题，包括角度和计算数值的数据格式。

综合考虑上面提到的问题，在FPGA设计中本文采用变象限法，单步流水线技术和相幅量化数据格式这3种技术，图3为CORDIC算法相/幅转化原理框图。

图3 CORDIC算法相幅转换原理图

CORDIC算法的基本原理是：通过相位累加器输入一个16 bits的二进制数，取其中高2位用来分辨收到相位所在的象限，随后分别将高2位发送给前处理单元和延迟单元，前处理单元根据接收到的数据进行处理，处理结果送入CORDIC算法单元，即流水线结构。延迟单元和CORDIC算法单元同步输出结果，保存输入数据高2位用于恢复结果到原来象限，并输出结果。

1）前处理单元基本原理

前处理单元是负责将相位值变换到第1象限并把高2位送入延迟单元，并送入CORDIC算法模块进行迭代计算。

①当高2位为“00”时，输入相位为第1象限，相位值不变，直接传给CORDIC模块；

②当高2位为“01”时，输入相位为第2象限，相位值减去16d16384（90°），同时传给CORDIC模块；

③当高2位为“10”时，输入相位为第3象限，相位值减去16d32768（180°），接着传给CORDIC模块；

④当高2位为“11”时，输入相位为第4象限，相位值减去16d49152（270°），同样传给CORDIC模块。

2）后处理单元基本原理

①当接收到的高2位是“00”，表示第1象限，输出的正余弦值都不变：

②当接收到的高2位是“01”，表示第2象限，输出结果做如下变换：

③当接收到的高2位是“10”，表示第3象限，输出结果做如下变换：

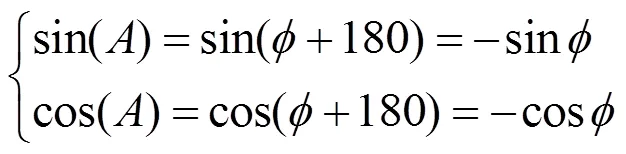
④当接收到的高2位是“11”，表示第4象限，输出结果做如下变换：

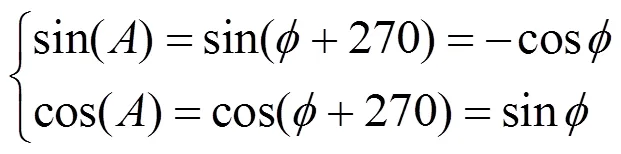
3）CORDIC算法流水线结构

图4 n级CORDIC算法流水线结构

3 结果与分析

从以上分析可知，运用流水线结构可以大大提高算法的实时性，其在处理速度上的优势是CORDIC算法用移位和加法代替乘法运算产生的。本设计采用的是16级流水线结构，只需等待16个时钟周期后就开始输出有效运算结果值，且在其后的每个时钟周期都会输出一个结果值，大大地提高了运算的效率。图5所示的是使用QuartusⅡ11.1实现的部分RTL级结构（包括2次迭代结构Cordic_interation[]）。

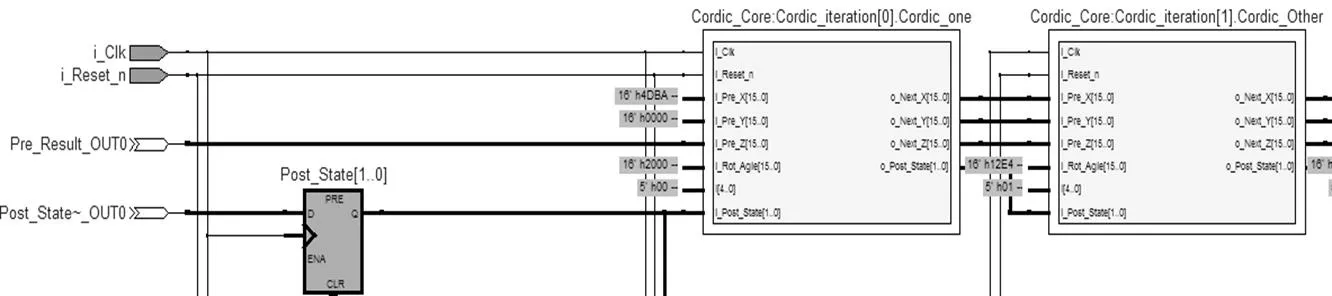
图5 FPGA实现的部分RTL级结构

下面2图是仿真产生的一个角度输出结果（图6）和正余弦结果（图7），其中输入时钟_Clk频率为100 MHz，输出正余弦频率为1 MHz，Accum_Reg是频率控制字FCW，sin和cos为输出正余弦信号。

图6 仿真输入一个角度输入结果

图7 仿真得到的正余弦结果

由以上仿真结果可知，CORDIC运算模块是经过16个周期延迟后开始连续地输出正弦结果，其与实际计算的正余弦值误差分析见表1。

表1 结果误差

表1表明，由这些具有代表性的仿真结果来看，实际值与理论值存在一定的偏差，但输入角度在一定范围内正弦函数的绝对误差很小，其精度非常高，而且可以随着结果位数的增加无限接近真实值，因此可以满足GNSS接收终端数字下变频的要求[10]。

4 结论

本文简单介绍了传统DDS系统的原理与结构和应用广泛的CORDIC算法，并结合变象限法、流水线技术及相幅量化数据格式针对CORDIC算法实现了正余弦信号的硬件设计，并能够在1个时钟周期内连续计算出函数值，通过对仿真结果分析可以得到所要求频率的正余弦波形，结果表明速度和精度都符合数字下变频对正余弦的要求，并且这个结构可以在现代电子系统设备及频率源设计中使用，具有较广泛的应用价值。

[1] 谢岗. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 181-286 .

[2] VOLDER J E, CONVAER A D, FORT W. The CORDIC trigonometric computing technique[J]. IEEE Transactions on Electronic Computers, 1959, 8(3): 334-334.

[3] WALTHER J S, PALO ALTO. A unified algorithm for elementary functions[J]. Spring Joint Computer Conference, 1971: 379-385.

[4] 李俊, 张晓东. 基于VB的串行通信在控制系统中的应用[J]. 机械电子, 2008, (10): 29-31, 32.

[5] 高泽溪, 高成. 直接数字频率合成器(DDS)及其性能分析[J]. 北京航空航天大学学报, 1998, 24(5): 615-618.

[6] 张正, 董少武, 张敏. 一种基于FPGA的多种波形发生器的设计[J]. 时间频率学报, 2008, 31(2): 133-137.

[7] 姚亚峰, 付东兵, 杨晓非. 高速CORDIC 算法的电路设计与实现[J]. 半导体技术, 2008, 33(4): 346-348.

[8] 耿丹. CORDIC算法研究与实现[J]. 遥测遥控, 2007, 28(S1): 39-42.

[9] 杨宏, 李国辉, 刘立新. 基于FPGA的CORDIC算法的实现[J]. 西安邮电学院学报, 2008, 13(1): 75-77.

[10] 何在民, 胡永辉, 武建锋. BPSK-R信号与BOC信号码跟踪性能分析及比较[J]. 时间频率学报, 2012, 35(2): 112-119.

FPGA implementation of CORDIC algorithm applied to digital down conversion

YAN Wen-he1,2,3, HU Yong-hui1,2, LI Jin-lin4, HE Zai-min1,2, WU Cheng-ying5, ZHAO Kun-juan1,2,3

(1. National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China;2. Key Laboratory of Precision Navigation and Timing Technology, National Time Service Center,Chinese Academy of Science, Xi′an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4.Information and Communication Branch of Hubei Electric Power Company, Wuhan 430077, China;5. Hubei University for Nationalities, Enshi 445000, China)

The sine and cosine signals are used in digital down conversion of GNSS receiver with important sense and the CORDIC algorithm is the most important way to implement the sine and cosine signals. According to the basic principle of DDS and CORDIC algorithm, aiming at the three existing problems in implementation of CORDIC algorithm, and combining the variable quadrant method, pipeline structure technique and phase/ amplitude quantization data format, we have realized the CORDIC algorithm with FPGA and thus the amplitude values of sine and cosine signals can be calculated in one clock cycle. The simulation results show that compared with the traditional CORDIC algorithm implementation the implementation presented in this paper is characteristic of a higher accuracy of the sine and cosine signals and a higher speed, meeting the needs of the digital down conversion of GNSS receiving terminal.

CORDIC algorithm; pipeline structure; sine and cosine signals; DDS(digital down-conversion)

P127.1

A

1674-0637(2014)01-0034-07

2013-03-08

中国科学院“西部之光”人才培养计划“西部博士资助项目”（Y307YR6601）

闫温合，男，硕士研究生，主要从事卫星导航定位与时间同步研究。