基于Ka频段的宽带信号数字下变频技术研究*

安卫国，达新宇，刘炜，郭威武

(空军工程大学，陕西 西安 710077)

0 引言

在频段超宽带卫星通信中，除了采用抗突发干扰、频谱利用率高的传输技术进行无线数据的高速传输外，信号接收技术也在很大程度上决定着通信系统的性能。数字下变频技术作为一种信号接收技术，以其较强的可控性和较高的精确度，已经发展成为多个领域的关键技术。如软件无线电、数字地面广播电视(digital video broadcasting-TV，DVB-TV)、数字音频广播(digital audio broadcasting，DAB)以及未来的4G通信技术。然而，数字下变频器的电路实现中涉及大量的乘加运算，这些运算通常用专用芯片或DSP实现，但是现有的DSP器件的处理速率已经没办法满足宽带信号下变频需求。

目前，已经有一些学者采用多相滤波数字正交变换[1]，数字混频正交变换[2]等[3-4]方法实现数字下变频，而实现上述理想变换的阶跃滤波器是很困难的；而文献[5]提到多通道的数字下变频高效结构，该方案先抽取后滤波最后混频，使系统在较低的速率下并行处理数据，大大地提高了运算的效率，但是该方案的接收信号是固定的某些带通信号，牺牲了频点的灵活性；文献[6]提出了一种改变滤波器带宽的方法，但是滤波器带宽成倍增加，容易引入不需要的干扰信号，不能准确地实现接收信号的频谱搬移；文献[7]提出了一种基于Goertzel滤波器的任意频点的高效数字下变频结构，但是该结构电路复杂，在实际实现上存在困难，电路消耗较多的运算能力，效率不高。

为此，本文从数字下变频的基本原理出发，分析其现有的高效结构，对文献[8-9]的高效算法进行推导，得出了非固定频点的高效数字下变频结构，最后用计算机仿真软件验证了该结构的有效性。结果表明改进后的高效结构可以实现非固定频点一定带宽信号的数字下变频。

1 数字下变频原理及多通道数字下变频结构

数字下变频的原理与模拟下变频一样，是把所需要的分量从中频载波频率搬移到所需要的频率[10]。图1为数字下变频一般结构图；接收信号经过ADC采样转换成高密度的离散数据序列x(n)与由数控振动器产生的复向量样本e-jω0n在数字混频器里相乘，然后对信号进行低通滤波滤除带外信息，从而对数字信息进行频谱搬移。

图1 数字下变频一般结构Fig.1 General structure of digital down conversion

对于一般的窄带信号来说，上述的一般数字下变频结构可以准确地实现接收信号的频谱搬移，而对于宽带信号来说，接收信号ADC后产生了较高的数据流，而现有的DSP处理器件无法满足高数据流的数字下变频任务；针对以上问题文献[5]提出了一种多通道的高效数字下变频结构，该结构先抽取后滤波最后混频，使系统在较低的速率下并行处理数据，结构图如图2。

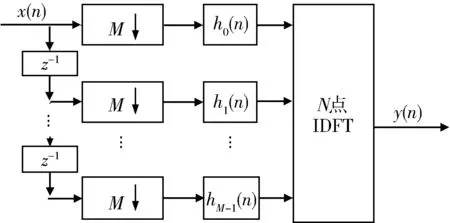
图2 多通道数字下变频结构Fig.2 Multi-channel digital down conversion structure

该方案对接收信号是有一定要求的，假设接收信号的采样频率为fs,信号的中心频率f0,抽取数M；根据信道化接收机原理，将整个调谐带宽分为N个信道，为了不出现盲区，每个信道的带宽为2fs/N，这样调谐带宽分为N组，相邻调谐通道之间有50%的重叠[11]； 调谐带宽划分如图3所示。

图3 调谐带宽分布Fig.3 Tuning bandwidth distribution

当接收信号正好落入某一信道且中心频点f0为某一信道的中心频点时，图2的结构是有效的，究其根本原因是牺牲了频点的灵活性来换取高效的数字下变频结构的。

2 基于多通道数字下变频的非固定频点的数字下变频高效结构

由图1下变频结构图可知，输出序列为

y(n) ={[x(n)e-jω0n]*h(n)}↓M=

(1)

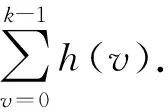
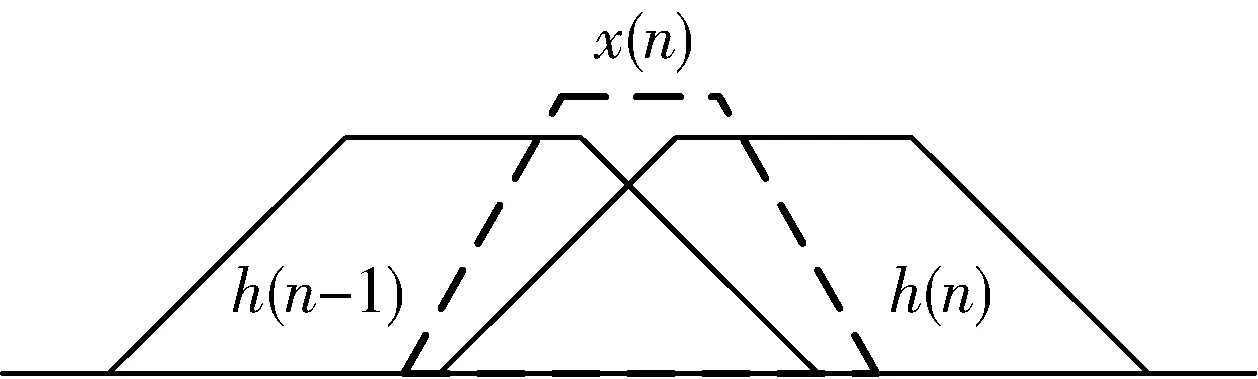
图4 f0不为m/M信号示意图Fig.4 Signal schematic diagram when f0 is not m/M

如果把宽带带通信号的中心频点分为周期分量f1和偏移量fd，周期分量为m/N，那么式(1)有：

y(n) ={[x(n)e-jω0n]*h(n)}↓M=

(2)

对式(2)进行多相分解，令v=ρ+lM，M为抽取倍数，式(2)得到

ej2πfd(ρ+lM)x(nM-(ρ+lM)).

(3)

比较式(3)与现有的多通道数字下变频结构，可以知道式(3)也将下变频结构分成了M个通道，其对接收信号的处理过程也是先抽取后滤波最后混频，但区别就在于滤波器组的各级滤波阶数的系数，式(3)中将混频系数的偏移分量ej2πfdn分散于各级滤波器中，使原本的滤波系数h(n)变为了h(n)ej2πfd(n)，然后对滤波后的离散点进行N点的IDFT，由于混频系数的不固定，对于输出的N点IDFT还需与周期分量的M被抽取后的混频系数作复乘运算，得到最后的频谱搬移后的输出序列y(n)。

图5为根据公式(3)得到的改进后的非固定点的数字高效下变频结构。

图5 改进的非固定频点数字下变频高效结构Fig.5 Improved non fixed frequency point digital down conversion efficient structure

由以上的结构可以知道，改进后的方案在结构上没有太大的变化，在每阶滤波器上复乘上一个频率偏移分量，如果接收机的抽取倍数为M，那么每处理一个点就相当于在原有的高效结构上多进行M+1次复乘运算，运算量有所增加，但是增加了频点的灵活性，相比文献[6]提到的基于Goertzel滤波器的电路实现结构来说，本文提到的结构更易于工程上的实现。

3 仿真验证

为了验证改进结构的有效和高效性，按照图5的改进结构和式(3)在计算机上用模拟仿真软件Matlab进行了仿真验证[12]；仿真条件如下：

原始输入信号为中心频点f0=22 MHz，带宽B0=8 MHz的线性调频信号；系统的采样率fs=100 MHz，N=10，M=5；由仿真条件可知输入信号落入划分频带的第2个信道内，该信道的中心滤波频点为20 MHz；仿真结果如图6所示。

图6 原始信号的频谱图Fig.6 Spectrum diagram of original signal

为了使下变频后的信号有可对比性，对原始信号按照图1的一般结构进行直接数字下变频，直接数字下变频的频谱结果如图7所示。

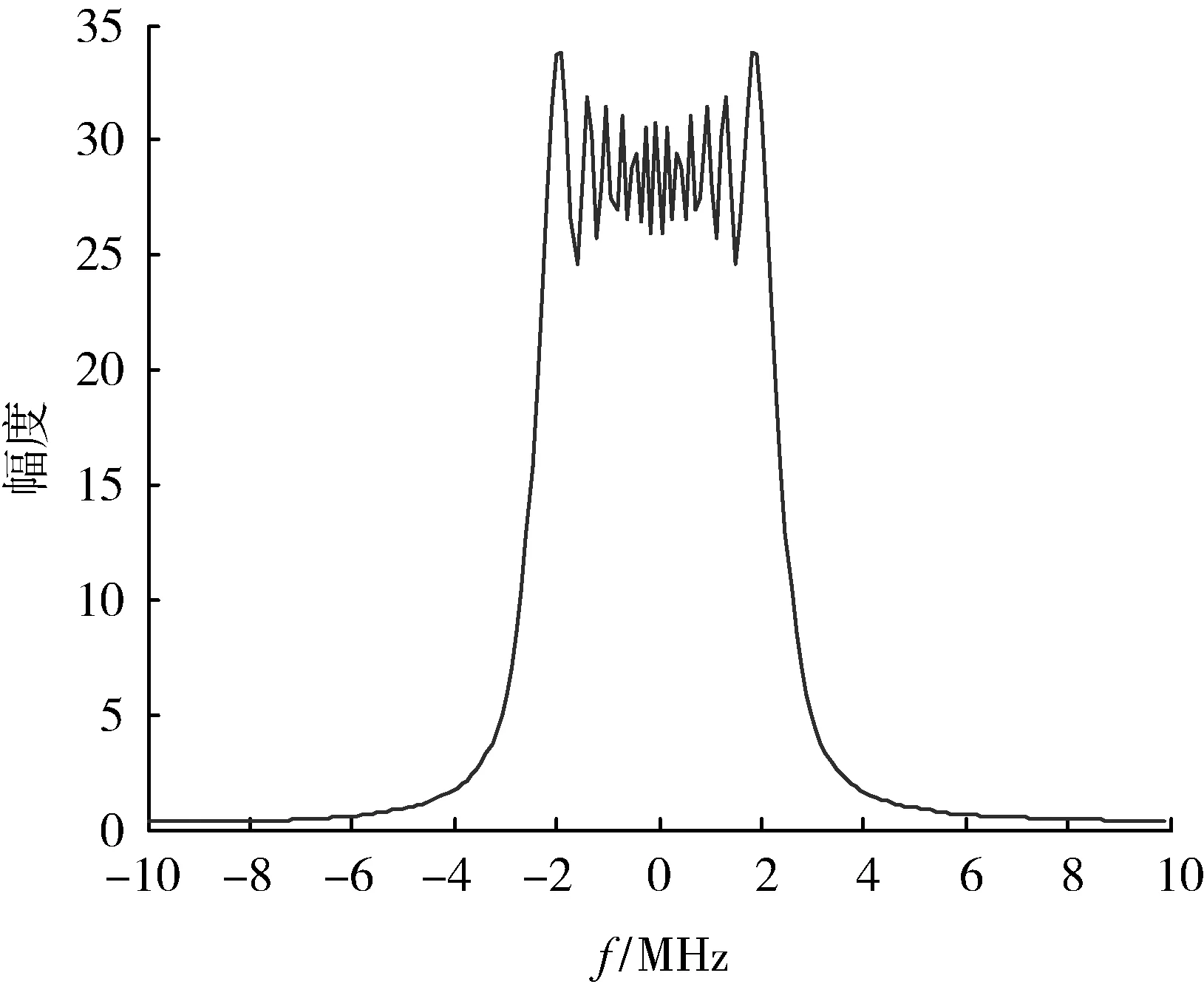
图7 对信号直接下变频后频谱图Fig.7 Direct down conversion signal spectrogram

如果对于一般的接收信号，其频点和带宽都不满足传统的多通道数字下变频基本条件，其下变频后的结果如图8所示。

图8 传统高效结构输出频谱图Fig.8 Traditional efficient structure output spectrum figure

按照式(3)和结构图5进行的改进后的下变频结构对一般特性的接收信号进行数字下变频结果如图9所示。

图9 改进结构的非固定频点下变频频谱图Fig.9 Improvement of structure of non-fixed frequency down conversion spectrum

由以上仿真图可以看出，图7是对接收信号进行原始的频谱搬移(按图1的原理结构)，图8是在传统的多通道数字下变频结构上实现的仿真，可以看出由于滤波器的限制，最后得到的输出序列相比图7的直接下变频输出是完全失真的，所以该方案不适合一般频点的数字下变频；图9则是采用了改进后方案的频谱输出图，相比较图7该方案输出的频谱实现了频谱的准确搬移，但是在频谱的幅度上有一些失真，这是由于滤波器组各级与频率偏移分量进行复乘过程中所产生的误差。

综上所述，改进的高效结构对非固定频点的带通信号进行数字下变频时，可以无失真地对信号进行频谱搬移，其下变频的频谱图等效于直接数字下变频的频谱图，而传统的多通道高效数字下变频对非固定频点进行数字下变频时对信号造成了不可还原的失真，其高效结构的有效性遭到破坏。

4 结束语

本文分析了现有的高效数字下变频结构，并针对已有结构频点固定的问题，将下变频系数分散于各个滤波器阶数中，得到了一种非固定频点的高效数字下变频结构，仿真验证了改结构的有效性。与传统结构相比运算量增加K+1次，但其接收信号的频点灵活性大大增加，在一定程度上提高了频段超宽带卫星通信系统的通信效率，具有一定的理论价值。

参考文献：

[1] Jou Shyh-jye,WU Shou-yang,Chorng-Kuang Wang. Low-Power Multirate Architecture for IF Digital Frequency Down Converter[J].IEEE Transactions of Circuits and Systems-Ⅱ:Analog and Digital Signal Processing,1998,45(11):1487-1494.

[2] Micheal Lohning,Tim Hentschel, Gerhard Fettweis.Digital Down Conversion in Software Radio Terminals[C]∥Proceedings of the 10thEuropean Signal Processing Conference Tampere,2000:1517-1520.

[3] 王韬，付连庆,杨力生，等.改进的多通道数字下变频技术与实现[J].兵工学报，2010，31(12)：1653-1658.

WANG Tao,FU Lian-qing，YANG Li-sheng,et al.Optimized Multi-Channel DDC Technology and Its Implementation[J].ACTA ARMAMENTARII，2010，31(12)：1653-1658.

[4] 邓晓平，田茂，罗义军，等.通用多通道数字下变频器的优化与实现[J].仪器仪表学报,2011，32(9)：1993-1997.

DENG Xiao-ping,TIAN Mao,LUO Yi-jun,et al.Optimization and Implementation of Universal Multi-Channel Digital Down-Converter[J].Journal of Scientific Instrument， 2011,32(9):1993-1997.

[5] 高志成，肖先赐. 宽带数字下变频的一种高效实现结构[J].电子与信息学报，2001,23(3)：255-260.

GAO Zhi-cheng,XIAO Xian-ci.An Efficient Implementation Architecture for Wideband Digital Downconversion[J]. Journal of Electronics & Information Technology, 2001,23(3)：255-260.

[6] 张嵘,肖先赐.任意中频带通信号多相数字下变频方法[J].电子与信息学报，2003,25(9)：1285-1289.

ZHANG Rong,XIAO Xian-ci.Polyphase Based Digital Downconvertion of Random IF Signals[J]. Journal of Electronics & Information Technology, 2003，25(9)：1285-1289.

[7] 李冰，葛临东,郑瑾. 一种改进的宽带数字下变频高效结构[J].电子与信息学报，2007，29(8)：1891-1894.

LI Bing,GE Lin-dong，ZHENG Jin.An Improved Efficient Architecture for Wideband Digital Down Conversion[J].Journal of Electronics & Information Technology, 2007，29(8)：1891-1894.

[8] WALDEN R H.Analog-to-Digital Converter Survey and Analysis[J]. IEEE Journal on Selected Areas in Communications,1999,17(4):539-550.

[9] FUDGE J,LEGAKO M，SEHREINER C. An Approach to Efficient Wideband Digital Down Conversion[C]∥Proc ICSPAT,Toronto, 1998:713-717.

[10] 粟欣，许希斌.软件无线电原理与技术[M].北京：人民邮电出版社，2009.

SU Xin,XU Xi-bin.Software Radio Principle and Technology[M].Beijing:Posts & Telecom Press,2009.

[11] 方勇.数字信号处理[M].北京：清华大学出版社，2010.

FANG Yong.Digital Signal Processing[M].Beijing:Tsinghua University Press,2010.

[12] 于彬.MATLAB数字信号处理[M].北京：机械工业出版社，2010.

YU Bin.MATLAB Digital Signal Processing[M].Beijing:China Machine Press,2010.