移动载荷下桥梁速度响应小波分析多裂纹识别
耿 佳,张伟伟,赵子龙,耿佳杨
(太原科技大学应用科学学院,太原 030024)
土木结构坍塌事故会给人类的生命及财产带来巨大的损失[1]。桥梁作为交通工具的重要组成部分,一旦发生坍塌事故会造成无法挽回的生命财产损失[2],所以对桥梁进行监测,在结构发生早期损伤时及时发现并采取相应的加固措施成为桥梁管理的重要组成部分。
在桥梁工程中,移动载荷是“车辆-桥梁”系统中对车辆载荷和重物载荷的简化模型。自2000年以来,如何利用桥梁结构在移动载荷下的动态响应进行结构损伤识别受到了越来越多的研究人员的关注。王步宇,俞亚南[3]研究了利用移动载荷作用下结构的振动响应幅值和非线性特征的变化来提取有关结构的损伤信息;徐伟华,吕忠荣等[4]人研究了基于多跨连续桥梁的某一桥梁物理参数在移动在移动载荷作用下的响应灵敏度的有限元模型修正法来识别结构局部损伤;杜永峰,刘云帅等[5]研究了移动载荷作用下简支梁某一点挠度解析解,在理论上证明了挠度差值影响线对损伤的识别。Li和Law[6]利用数学方法模拟了移动载荷和具有损伤的桥梁结构的特性,在此基础上研究了基于桥梁结构在移动载荷作用下的响应敏感性作为损伤指标的损伤识别方法,并讨论了在不完备测量条件下该方法的识别精度。
小波理论作为非稳态信号处理的先进方法,在结构损伤检测中具有广泛的应用。其理论基础为结构中的损伤必然会导致结构动态响应的奇异点,小波分析适合于检测信号中的奇异点,该方法只需要测量桥梁少数几个点的响应信号,利用小波分析实现损伤定位和评估,具有理论明确,操作简单的特点。2006年,Zhu和Law[7]利用移动载荷作用下桥梁中点位置的挠度响应信号作为损伤识别依据,并利用如图1(a)所示的Mexican hat 小波对该响应进行损伤识别分析,从而获得结构局部损伤的损伤参数,结果表明该方法不仅可以识别出裂纹的位置而且还可以指示裂纹的深度;Khorram A[8]提取了移动载荷作用时梁中点动态响应,利用Gaussian-4小波进行损伤识别。为了量化损伤程度,作者依据小波变换局部极值定义了损伤指标,并利用因子设计给出了梁长高比、损伤位置以及损伤深度与损伤指标之间的显示表达。Nguyen K等[9]应用多自由度的机车在梁式结构上移动的模型,将位移传感器布置在车辆模型上来并提取随时间变化的位移响应信号作为小波分析的输入信号,分析了位置为L/3和2L/3处深度相同的损伤,而并未对裂纹个数变化以及裂纹深度随裂纹位置不同时的识别进行研究,而且测量结果很容易受到干扰; Khorram A[10]提取移动载荷作用下中点位置的挠度响应信号作为如图1(b)所示Gaussian-4小波分析的输入信号,进行多处损伤定位分析,并利用小波系数局部极大值建立了损伤指标DI,从而指示裂纹的大小。
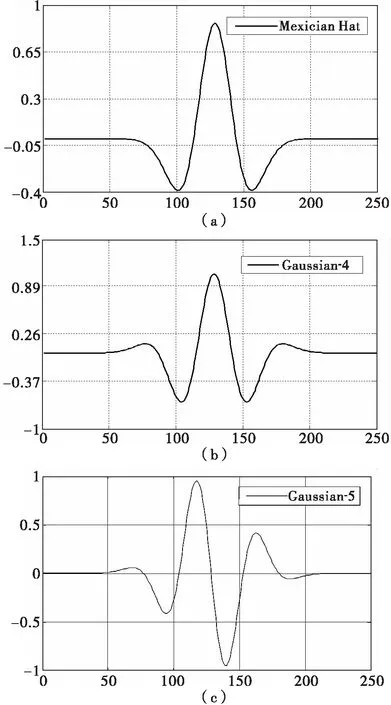
图1 Mexican Hat、Gaussian-4和Gaussian-5小波Fig.1 The wavelet of Mexican Hat,Gaussian-4 and Gaussian-5
在移动载荷下,桥梁动态响应包括位移、速度和加速度,现有文献主要讨论了位移和加速度在损伤识别中的应用。已知速度和加速度可以由位移求导获得,因此,和位移相比,速度和加速度有望获得更高的灵敏度。同时,加速度对信号的局部特征更为敏感,易受噪声影响。基于此,将检验速度响应作为结构损伤检测基础信号的有效性,考虑到实际工程中多处裂纹同时发生,将对利用速度响应识别结构多位置裂纹损伤将重点描述,并对噪声以及载荷速度对识别效果的影响进行深入讨论。
1 梁的运动方程
1.1 无裂纹梁运动方程
在移动载荷作用下无裂纹梁的力学模型如图2所示。该梁承受移动载荷P(t),其运动方程为:
(1)
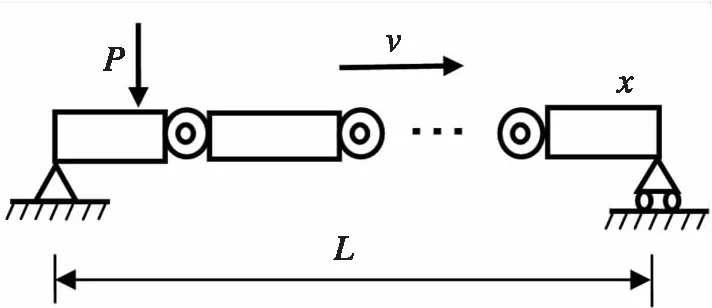
图2 无裂纹梁的力学模型Fig.2 The model of intact beam
边界条件为:
(2)
初始条件为:
(3)
方程(1)的解为:
(4)

(5)
对式(5)求导可得到梁中点的速度为:
(6)
1.2 裂纹梁运动方程
当梁中存在裂纹时,可将其简化为由扭转弹簧连接的多个Euler-Bernoulli子梁[6],如图3所示。其中扭转弹簧在裂纹处。图3所示含有离散裂纹的梁结构在移动载荷作用下第i部分的欧拉伯努利特征函数ri为:
ri(xi)=Aisinβxi+Bicosβxi+Cisinhβxi+Dicosβxi,
(i=1,2,…,N+1)
(8)

图3 裂纹梁的力学模型Fig.3 The model of crack beam
β是该梁的特征值。
边界条件为:
r1(xi)x1=rN+1(xN+1)|xN+1=lN+1=0
(9)
(10)
ri(xi)|xi=li=ri+1(xi+1)|xi+1=0
(11)
(12)
(13)
(14)
由此可得该裂纹梁的模态函数为:
φ(x)=r1(x)[1-H(x-l1)]+
(15)
其中H(x)是单位长度阶梯函数。
则裂纹梁中点的挠度响应为:
(16)
求导可得该裂纹梁中点的速度响应为:
(17)
2 利用连续小波变换识别裂纹
在式(16)所示的含有结构模态振型函数的响应中由于在裂纹处不连续而存在突变点,这些突变点会在结构的速度响应曲线中成为奇异点,这些奇异点是无法直接观察出来的。连续小波变换作为信号处理工具的出现使得识别信号中所包含的奇异点(损伤)成为可能,并且可以识别出损伤参数[11]。小波变换的一般表达式为:
(18)
其中ψ(t)为母小波,ψ(t)经过平移和伸缩之后就成为一个小波序列即ψa,b(t).从桥梁损伤识别的工程角度来看,奇异点就是信号中的突变点即损伤点,而奇异性则是关于奇异点突变程度的定性描述。小波变换对于奇异点的识别一般采用如下表达式:
(19)
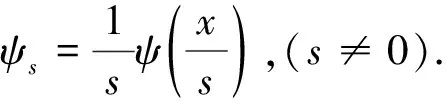
(20)
当s→0时,小波反应了x点的局部形态,式(20)就是可以用来观察信号中存在的微小变化[12]。因此小波变换可以用来判断函数(信号)的局部性态,亦即局部正则型,由Lip指数的概念知函数(信号)的正则型就反映了函数(信号)的奇异性。
小波变换对奇异点的指示包括小波系数曲线过零点和极值点两种方式,也就是说突变点的位置有时是由小波系数曲线的过零点表示的,有时是由极值点表示的。一般说来过零点检测奇异点效果较差,因为过零点易受噪声的干扰,而且有时反映的不是信号的突变点而是信号在慢变区间的转折点。而不同对称性质的小波基对于阶跃信号和突变信号的奇异性的指示方式是不同的,对称小波基以极值点表示突变信号的奇异点,而反对称小波基以极值点表示阶跃信号的奇异点。由文献[13]中知,移动载荷作用下梁中点的速度响应信号是阶跃的而位移响应是突变的。所以为了获取较好的识别效果,本文选取图1(c)所示具有反对称性质的Gaussian-5小波基来分析速度响应信号。
3 数值研究
为了验证上述方法的可行性,文献[7]中的简支梁模型将被应用于本文的损伤识别研究中。几何参数和材料属性如表1所示。

表1 模型几何物理参数Tab.1 Parameters of the beam
为了简化运算,取材料阻尼比为0.02.移动载荷下桥梁动态响应将利用Ansys瞬态动力学分析模块求解,采用shell63单元,由于数值分析结果显示裂纹识别结果与裂纹宽度无关,故单元大小设定为0.1 m×0.1 m.裂纹参数xc(xc=裂纹位置距离左边界的距离/梁长渡)和a(a=裂纹深度/梁高度)分别表示裂纹相对于左边界的位置和裂纹大小。本文利用删除单元的方法在有限元计算中模拟梁结构的裂纹。图4和图5所示为无阻尼简支梁在速度为5 m/s和15 m/s移动载荷作用下中点位置的挠度和速度响应的模拟和解析结果。从中可以看出,Ansys结果具有良好的求解精度。
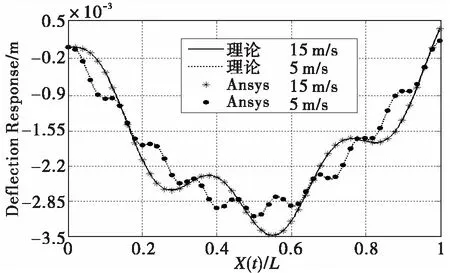
图4 梁中点挠度响应Fig.4 The deflection response at mid-span
为了比较该方法识别损伤的优点,对同一损伤分别利用速度响应Gaussian-5小波和位移响应的Gaussian-4、Mexican hat小波来分析,结果如图6所示。从图6中可以看出中点速度结果的Gaussian-5小波分析对损伤的识别结果比挠度Gaussian-4更加灵敏同时也比挠度Mexican hat小波的识别结果更容易观察出裂纹的位置,指示也更精确。所以本文将选取Gaussian-5小波和中点速度结果进行多裂纹损伤识别研究。
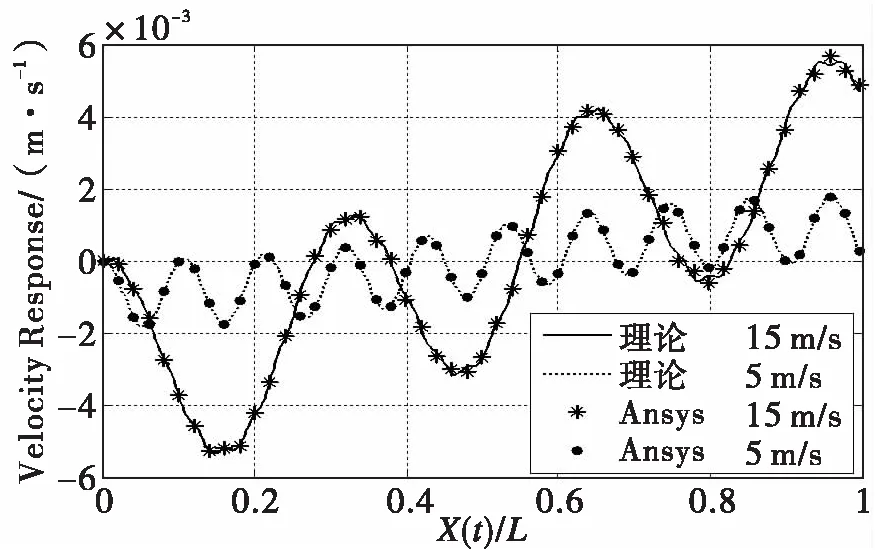
图5 梁中点速度响应Fig.5 The velocity response at mid-span
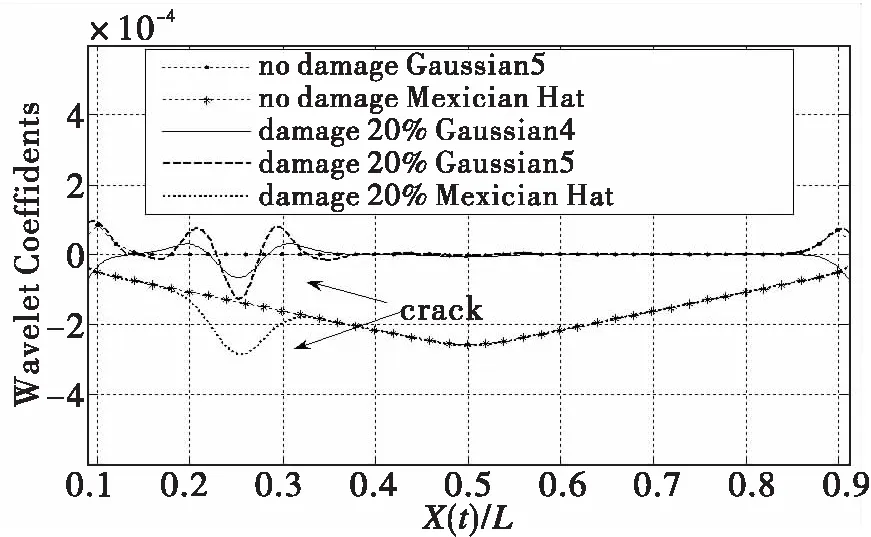
图6 损伤的识别方法比较Fig.6 The comparison of damage detection methods
3.1 多位置损伤识别
为了进一步说明本文所提的方法,对表2所列算例将利用上述方法进行识别。
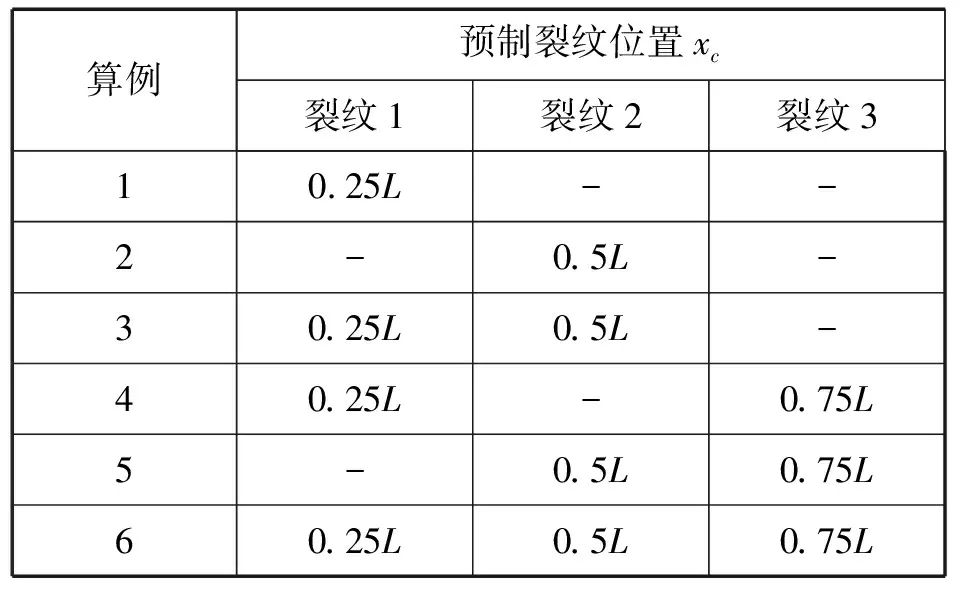
表2 损伤识别算例Tab.2 Parameters of different cases
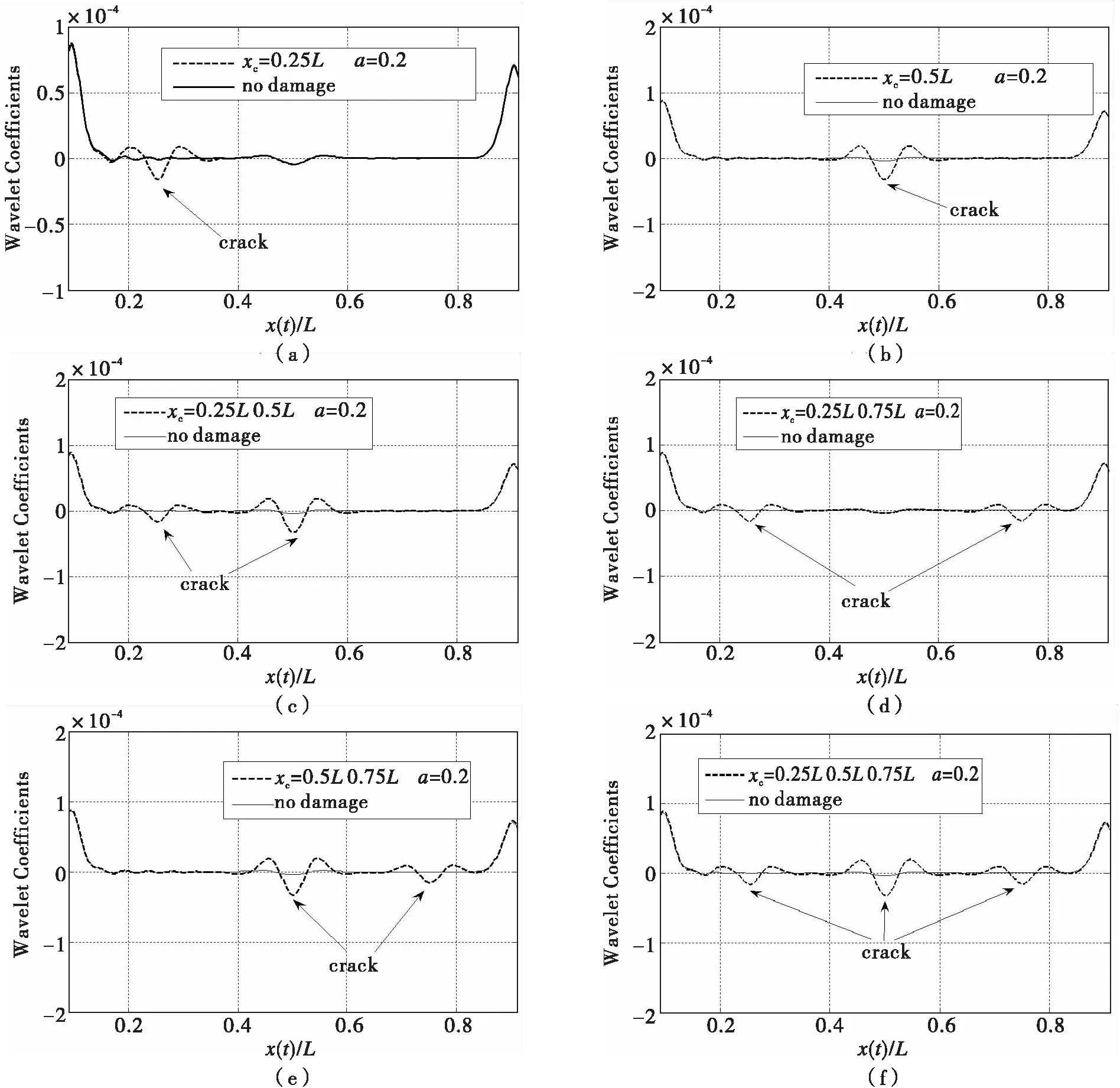
图7 算例1到6损伤识别结果与未损伤时的对比Fig.7 Wavelet transform of velocity responses for both intact and damaged beam
为对比计算结果,令载荷移动速度为2 m/s,裂纹深度a为0.2.图7显示了给出了各算例经过连续小波变换以后的损伤识别结果。可以看出,无论是单一位置损伤还是多处位置损伤,该方法均可以准确指示出来裂纹位置。为了可以直观对比识别结果的准确性,将该方法的识别结果的小波系数极值点数据和裂纹位置进行对从而得到如表3所示的损伤识别算例及识别结果。可以看出,利用该方法识别裂纹位置的最大误差为0.6%,可满足工程需要,并且裂纹位置的识别结果不受其他裂纹的影响,具有非常好的独立性。
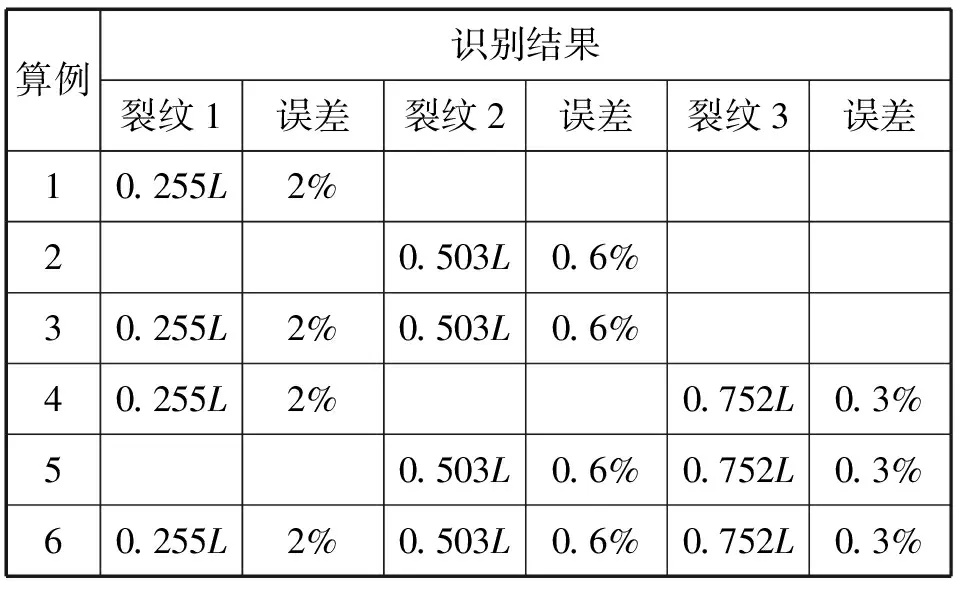
表3 算例识别结果Tab.3 Results of different cases
3.2 裂纹深度识别
为了进一步研究裂纹深度随小波系数局部极大值变化的关系,对表4中所列同一位置,不同裂纹深度的算例也进行小波分析。

表4 不同裂纹深度参数Tab.3 Parameters of different crack depths
图8和图9给出了裂纹位置分别为0.25L和0.5L时不同裂纹深度下的小波变换系数。
并将图10和图11中随着裂纹深度不断变化的小波系数(为了能够清楚表达变换关系,图中裂纹深度a为0.1、0.2和0.4)局部极大值分别为横纵坐标建立深度与局部极大值之间的变化关系,从图中可见,当裂纹深度逐渐增加时,小波系数局部极大值也随之增加,这一规律可用来识别裂纹深度。为此,定义小波系数局部极大值为损伤指标DI为:
DI=max|WF|
(18)
分别由图7和图8中不同裂纹位置的深度和小波系数局部极大值之间的变化关系建立裂纹深度与损伤指标DI之间的变化关系,从而得到如图9所示小波系数局部极大值与裂纹深度的关系曲线。从图中可以看出不同位置的小波系数局部极大值随着裂纹深度的增加也在不断上升,所以以该方法建立的以小波系数局部极大值DI为损伤指标可以用来指示损伤的大小。
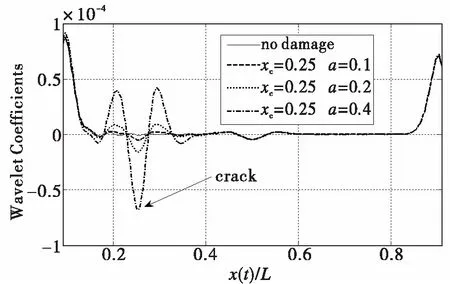
图8 小波系数局部极值变化规律(裂纹位置为0.25L)Fig.8 The identification results for differentcrack depths at 0.25L
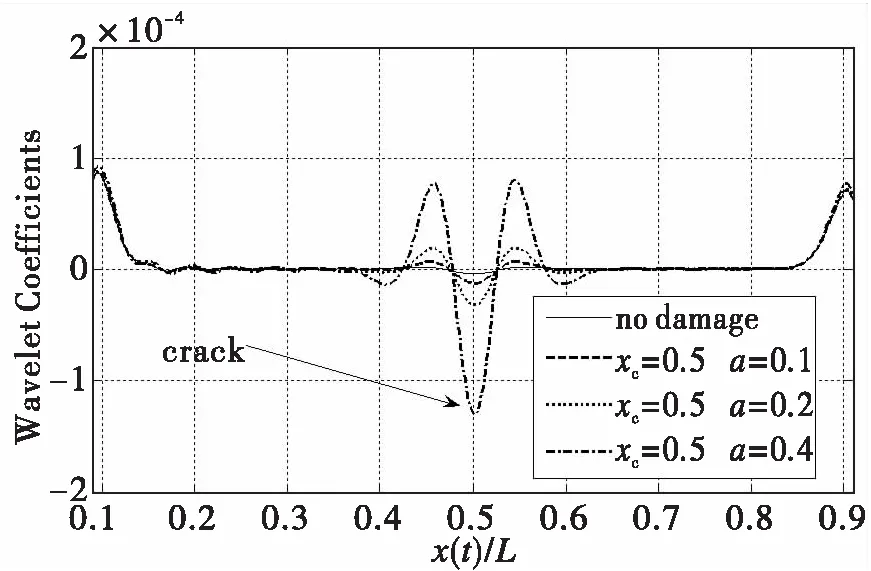
图8 小波系数局部极值变化规律(裂纹位置为0.5L)Fig.8 The identification results for differentcrack depths at 0.5L
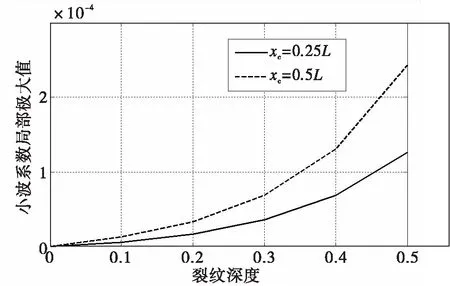
图9 裂纹深度与损伤指标DI间的关系曲线Fig.9 The curve of relation between crack depth and DI
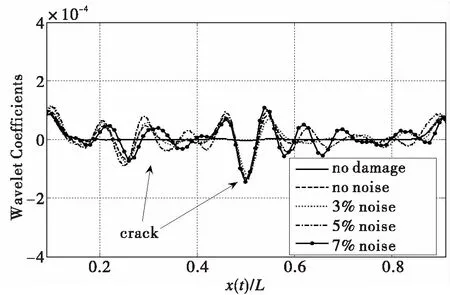
图10 不同噪声水平对识别结果的影响Fig.10 The identification results for different noise levels
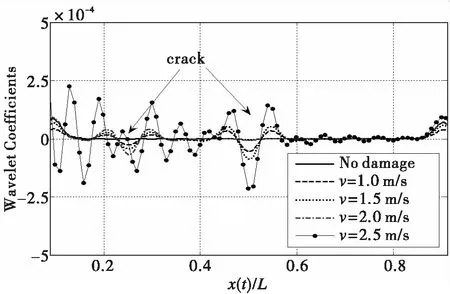
图11 裂纹识别结果随移动载荷速度大小的变化规律Fig.11 The identification results for different velocitiesof moving loads
3.3 参数对识别结果的影响
由于实际测量环境中难以避免噪声影响,同时载荷速度也是影响损伤检测的重要指标,本节将对噪声影响和载荷速度进行深入讨论。以上的裂纹识别研究结果都是基于没有环境噪声、移动载荷速度固定为v=2 m/s.为了进一步说明该方法对于多处裂纹识别,研究不同的噪声水平和载荷速度对于识别结果的影响。将噪声水平分别为3%、 5%和7%加到中点速度响应结果中,对含有噪声的信号进行小波变换的损伤识别分析,得到如图10所示识别结果,此时载荷移动速度仍取为2 m/s.从图中可以看出,在噪声水平逐渐增大时,出现干扰越来越严重从而不利于识别损伤,不过在噪声水平为7%时,仍可以较好的识别出两处损伤。进一步研究发现,当噪声水平大于10%时无法观测出裂纹所在位置。
对于速度影响,本文考虑裂纹位置xc分别为L/4和L/2,损伤程度a都为0.4的损伤梁模型,载荷移动速度v分别为1 m/s、1.5 m/s、2 m/s和2.5 m/s时中点位置的速度响应进行损伤识别 (分析尺度scale为24),得到如图11所示的损伤识别结果,可以看出随着载荷速度的增加损伤识别结果的小波系数曲线会出现一些波动。在速度较小时,识别效果较好,但是当速度较大时(如2.5 m/s),产生的波动已经很明显而且已经很难从小波系数曲线中观察出裂纹的位置。综上所述,使用该方法来识别损伤时需要选取合适的移动载荷速度。
4 结论
讨论了利用简支梁中点速度响应连续小波变换的结构多损伤识别方法。研究结果表明,利用梁中点速度响应的Gaussian5小波分析识别损伤的方法不仅可以定位出不同裂纹所处的位置,同时小波系数局部最大值会随损伤程度增加而增加,由此将小波系数局部极大值(DI)作为损伤指标,讨论了损伤指标随损伤程度的变化规律。此外,对噪声和载荷速度对识别结果的影响进行了比较研究,数值算例表明,即便噪声为10%,该方法仍可以有效的识别损伤位置;在速度较小时,识别效果较好,因此,在利用本文方法进行结构损伤识别时,载荷速度不宜过大。
参考文献:
[1] 李宏男,高东伟,伊廷华.土木工程结构健康监测系统的研究[J].力学进展,2008,38(2):151-166.
[2] 徐洪涛,郭国忠,蒲焕玲,等.我国近年来桥梁事故发生的原因与教训[J].中国安全科学学报,2007,17(11):90-95.
[3] 王步宇,俞亚南.移动荷载作用下结构损伤的近似熵分析[J].振动与冲击,2010,29(6):125-128.
[4] 徐伟华,吕中荣,刘济科.基于移动载荷响应的多跨连续桥梁损伤检测[J].力学与实践,2008,30(5):49-52.
[5] 杜永峰,刘云帅,王晓琴.基于挠度差值影响线的简支梁桥损伤识别研究[J].甘肃科学学报,2009,21(4):89-92.
[6] LI J,LAW S S.Damage identification of a target substructure with moving load excitation[J].Mechanical Systems and Signal Processing,2012,30:78-90.
[7] ZHU X,LAW S.Wavelet-based crack identification of bridge beam from operational deflection time history[J].International Journal of Solids and Structures,2005,43:2299-2317.
[8] KHORRAM A,NEJAD F B,REZAEIAN M.Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load[J].International Journal of Engineering Science,2012,51:204-215.
[9] NGUYEN K V,TRAN H T.Multi-cracks detection of a beam-like structure based on the on-vehicle vibration signal and wavelet analysis[J].Journal of Sound and Vibration,2010,329(21):4455-4465.
[10] KHORRAM A,REZAEIAN M,NEJAD F B.Multiple cracks detection in a beam subjected to a moving load using wavelet analysis combined with factorial design[J].European Journal of Mechanics A/Solids,2013,40:97-113.
[11] PANDEY A K,BISWAS M,Samman M M.Damage detection from changes in curvature mode shapes[J].Journal of Sound and Vibration,145(2):321-332.
[12] 任宜春,李峰.连续小波变换在梁结构损伤诊断中的应用研究[J].振动、测试与诊断,2004,24(2):121-124.
[13] GONZA′LEZ A,HESTER D.An investigation into the acceleration response of a damaged beam-type structure to a moving force [J].Journal of Sound and Vibration,2013,332(13):3201-3217.

