基于Simulink的忆阻器模型

宋卫平，丁山传，宁爱平

(太原科技大学 电子信息工程学院，太原 030024)

蔡少堂教授在1971年根据电路理论的完备性，提出了忆阻器的定义[1]。2008年惠普实验室制造出了首个纳米级的忆阻器物理模型，并通过实验证明了忆阻器是一种具有记忆功能的无源非线性二端电路元件[2]。忆阻器作为第四类基本元器件，能够有效提升电路的集成度[3]；简化混沌电路的电路结构[4]；为研制新型计算机开辟道路[5]；并有望把人工神经网络的信息处理方式和非易失性模拟存储器变为现实[6]。但对大多数研究者来讲，忆阻器的物理模型难以得到，所以建立精确的仿真模型就显的至关重要了。

本文首先在忆阻器的理论基础，研究了惠普忆阻器模型的电路关系，然后在Simulink中用二种不同方法对忆阻器进行仿真。方法一通过受控电压源实现对于忆阻器阻值变化的模拟。方法二通过在Simulink环境下应用Simscape系统提供的非线性电阻来实现对于忆阻器阻值变化的模拟。这两种方法不但能够方便准确的观察忆阻器的输入输出特性，而且具有与其他器件相结合的能力。因此这两种模型不但适合于对忆阻器性质的研究，而且适合于对忆阻器应用的研究。

1 数学模型

根据蔡少堂教授提出的定义[7]，在电路分析中，忆阻器的基本数学定义表达式是一个微分方程：

v=M(q)i或i=W(φ)v

(1)

其中v和i分别为忆阻器两端的电压和电流；M，W为忆阻器的忆阻和忆导[7]，定义为：

(2)

图1是惠普实验室制造的忆阻器物理模型[8]，它是将两层纳米级的二氧化钛薄膜夹在两个铂片内，其中一层掺杂有氧空位，相当于半导体，另一层没有掺杂有氧空位，相当于绝缘体。

图1 忆阻器物理模型Fig.1 Physical model of memristor

D表示忆阻器总厚度，约为10 nm.w表示掺杂层的厚度，并随着流过忆阻器的电荷数改变。忆阻器的总阻值可表示为：

Rmem(x)=Ronx+Roff(1-x)

(3)

其中，x表示如下：

(4)

Rmem表示总忆阻，Ron与Roff是w处于两个边界值时的临界阻值。x是掺杂层厚度与忆阻器薄膜总厚度的比值。

在惠普忆阻器中离子的迁移速率呈现十分显著的非线性，特别是在w接近0或者D时，离子的迁移速度会受到明显的抑制，以至于离子的迁移速度会减小到 0，所以引入窗口函数用来表示x与i之间的非线性关系。

(5)

其中μv为掺杂物迁移率，一般取μv=

10-14m2s-1V-1.

窗口函数[9]为：

f(x)=1-(2x-1)2p

(6)

在仿真时取参数Ron=100 Ω，Roff=16 000 Ω，忆阻器初始值Rinit=11 000 Ω，p=10.

2 基于受控源的双端口模型

在Simulink中忆阻器的模型可看成是具有记忆功能的非线性电阻，通过一个带反馈的积分器来实现忆阻器的记忆功能，通过窗函数f(x)来实现忆阻器中离子迁移的非线性特性，通过界面位置x来控制受控电压源实现对忆阻器阻值变化的调节，从而实现了对于忆阻器的双端口建模。

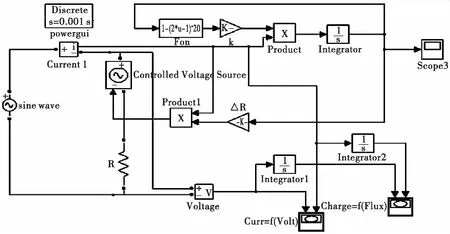
图2 双端口忆阻器模型Fig.2 Dual port model of memristor

根据方程(5)可得到：

(7)

用模块搭建出方程(7)。在Simulink中已经给出了积分器，在建模时可直接使用，fcn模块为窗口函数的数学表达式。

受控电压源的电压为：

E=-△Rxi

(8)

其中

△R=Roff-Ron

(9)

忆阻器的阻值Rmem为受控电压源E与阻值为Roff的电阻串联后对外等效的电阻值，即：

Rmem=Roff-△Rx

(10)

图中R为与w=0相对应的临界阻值Roff，输入模块为标准的正弦电压源，振幅为1 V，频率为1 Hz.

为了有更好的输出效果需要设置积分器的初始值：

(11)

设置电力系统图形化用户接口(powergui)为离散型，步长为0.001 s；微分方程的解算器为ode45；电荷和磁通通过电流和电压的积分直接得到。仿真所得到的图型如下：

图3中电流-电压关系为典型的磁滞回线，显示了忆阻器的开关特性，即忆阻值可以在高阻和低阻之间转换。同时，掺杂层厚度与忆阻器总厚度之比x在(0，1)内随输入电压做周期性变化。磁通量与电荷之间是一种非线性关系，随着磁通量增加，电荷量递增，反之递减，表明忆阻器是一种非线性元件。仿真结果显示双端口模型能够实现对于忆阻器建模。而且Simulink被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中，在Simulink中建立能够直接与其他器件相连接的双端口模型，具有更广泛的适应范围，为忆阻器的进一步研究提供了良好的参考。

图3 仿真波形Fig.3 Simulation waveform

3 基于Simscape的双端口模型

Simscape是Matlab中可用于对机械、电气、液压和热场以及其他多域物理系统进行建模和仿真的组件，它不但支持使用文本定义物理建模组件、域和库提供参数和变量的物理单位，而且能够自动进行单位转换。

忆阻器的Simscape物理模型框如图4。

通过一个带反馈的积分器来实现忆阻器的记忆功能，通过窗函数f(x)来实现忆阻器中离子迁移的非线性特性，直接应用Simscape模型库中非线性电阻来实现对忆阻器阻值变化的调节，从而实现了对于忆阻器的双端口建模。

图4 Simscape模型框图Fig.4.Principle memristor scheme in Simscape

图5 基于Simscape和Simulink双端口模型Fig.5 Physical memristor model in Simulink & Simscape

图中fcn模块为窗口函数的数学表达式；fcn、乘法器、放大器和积分器用来实现方程(7)，输出结果为掺杂层厚度与忆阻器薄膜总厚度的比值x；fcn.1为方程(10)的数学表达式，输出为忆阻器的阻值。Variable Resistor为Simscape中提供的三端口可变电阻模型，左右分别为输入和输出端，上端为控制端，器件的阻值跟随控制信号做连续变化。PS-Simulink Converter能够将物理信号转换成在Simulink中应用的无单位信号；Simulink-PS Converter能够将无单位的Simulink信号转换成Simscape中的物理信号，这样就实现了Simscape与Simulink的连接。模型的仿真结果如下：

仿真结果显示模型能够实现对于忆阻器的仿真，并且使用Simscape提供的各物理域基础模块来组装各种物理模型时，组件之间使用物理连接，所建立的模型能够清晰的反应出所开发系统的内部结构。Simscape与Simulink结合后可更加方便的对复杂的系统进行建模，为忆阻器的多学科应用打下了基础。

图6 仿真波形Fig.6 Simulation waveform

5 结论

本文在Simulink中应用两种不同的方法对忆阻器进行了建模，通过仿真结果可以看出这两种方法不但能够直观准确的展示忆阻器的输入输出特性，而且具有与其他器件相结合的能力，为人们学习和研究忆阻器特性提供了新的方法。田晓波[10]应用编写程序的方法实现了基于忆阻器的一阶无源滤波电路的仿真。段宗胜[11]应用忆阻器的SPICE模型，实现了基于忆阻器的高通滤波器的仿真。与这两种方法相比，应用基于Simulink的双端口模型进行仿真，无需书写大量程序，只需要通过简单直观的鼠标操作，就可构造出复杂的系统，并且具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点。所以本文提出的基于Simulink的双端口模型具有更加广阔的应用前景。

参考文献：

[1] CHUA L.Memristor-the missing circuit element[J].IEEE Trans Circuit Theory，1971，18(5)：507-519.

[2] STRUKOV D B，SNIDER G S，STEWART D R，et al.The Missing Memristor Found[J].Nature，2008，453：80-83.

[3] 段书凯，刘光远.连续学习混沌神经网络的研究[J].计算机科学，2004，31(4)：135-139.

[4] WANG L D，YANG X F.Generation of Multi-Scroll Delayed Chaotic Oscillator[J].Electronics Letters，2006，42(25)：1439-1441.

[5] WILLIAMS R S.How We Found the Missing Memristor[J].IEEE Spectrum，2008，45(12)：28-35.

[6] LEWIS D L，LEE H H S.Architectural Evaluation of 3D Stacked RRAM Caches[C]∥IEEE International Conference，2009：28-30.

[7] KAREL ZAPLATILEK.Memristor modeling in MATLAB[C]∥Proceedings of the European Computing Conference，2011：62-67.

[8] Zdeněk BIOLEK.SPICE Model of Memristor with Nonlinear Dopant Drift[J].RADIO ENGINEERING，2009，18(2)，210-214.

[9] ZHANG YU，ZHANG XULIANG，YU JUEBANG.Approximated SPICE model for memristor[C]∥ICCCAS(2009)，IEEE，2009：928-931.

[10] 田晓波.忆阻器电路特性与应用研究[D].长沙：国防科技大学，2009.

[11] 段宗胜.基于忆阻器的滤波器设计与仿真[D].武汉：国防科技大学，2012.