局部约束阻尼层耗散率一致化优化

梁培根，孙大刚，李占龙，高 蓬

(太原科技大学机械工程学院，太原 030024)

约束阻尼层具有高效、可靠的减振特点，广泛应用于车辆、潜艇舰船、航空航天等振动噪声控制领域。实际工程应用中，常根据结构振动情况在若干位置敷设约束阻尼层，即为局部约束阻尼层。然而，阻尼层增大了结构质量，不利于轻量化设计。为使一定质量的约束阻尼层产生最佳的减振效果，需对其进行优化。

材料确定后，局部约束阻尼层的减振效果与阻尼块的敷设位置、厚度参数密切相关[1]。Subramanian等[2]通过计算轿车光板复合模态应变能分布情况，对约束阻尼层位置与尺寸进行优化。敷设阻尼层后的结构与原结构的应变能分布并不相同，以原结构的应变能分布来确定敷设位置不是最佳。郑玲、郭中泽、王明旭、Alvelid等[3-6]分别采用优化准则法、渐近结构拓扑法、变密度法、改进梯度法，对约束阻尼层材料布局进行拓扑优化，得到了阻尼材料最优分布形状。Chia等[7]采用细胞自动机算法，研究了平板约束阻尼层的最佳粘贴位置问题。拓扑优化及细胞自动机算法仅能优化阻尼层的敷设位置，忽略了阻尼层厚度参数对其拓扑形状的影响，且在实际应用中计算量较大。杨加明等[8]采用改进遗传算法，优化了多层黏弹性复合结构的厚度参数。遗传算法全局搜索能力强，而收敛速度较慢。

具有多个阻尼块的局部约束阻尼层，设计变量多，仅优化单一变量并不能获得最佳解。本文综合考虑敷设位置与厚度参数对局部约束阻尼层减振效果的影响，仿照生物生长过程，提出了一种局部约束阻尼层耗散率一致化优化方法，实现了对约束阻尼层敷设位置和厚度参数的综合优化。通过四边简支板的算例，证明了该方法的可行性和有效性。

1 局部约束阻尼层优化

1.1 损耗因子关于质量的灵敏度

约束阻尼层由基层、阻尼层、约束层构成。根据模态应变能理论[9]，忽略约束层和基层材料损耗因子，则局部约束阻尼层的第r阶模态损耗因子为：

(1)

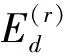
i号阻尼块的第r阶模态最大损耗因子关于质量的灵敏度可按下式计算:

(2)

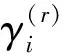
随着阻尼层及约束层厚度的增大，结构模态损耗因子增速逐渐减小[10]，约束阻尼层的耗散率逐渐减小。因此，阻尼块的耗散率总体上是其质量的单调递减函数，且不同阻尼块在质量相同时的耗散率不同。图1为不同阻尼块的耗散率随其质量的变化情况。

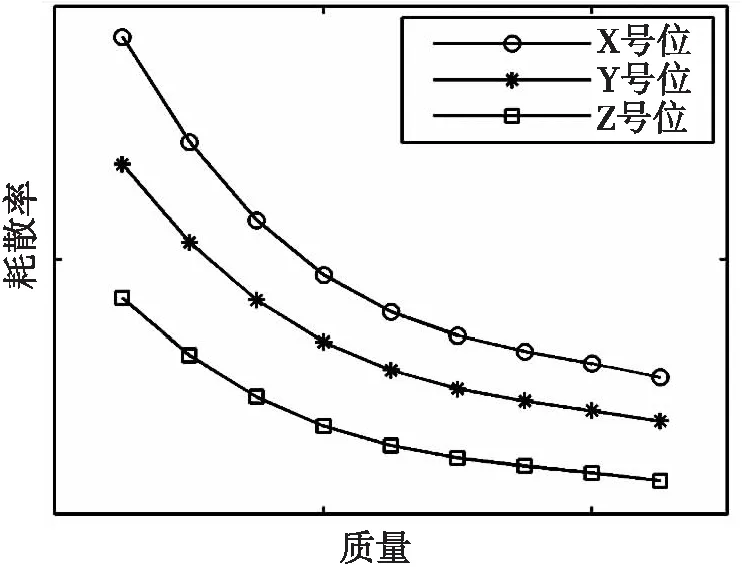
图1 耗散率随质量的变化趋势Fig.1 The tendency of dissipation rate with mass

1.2 优化模型

为使整个约束阻尼层减振效果最好，以附加阻尼结构质量为约束条件，将结构表面划分为n块区域，从中选择最优的若干区域，敷设多个厚度参数为最佳的阻尼块。当附加阻尼结构质量较小时，可认为，各阻尼块一起敷设时的最佳厚度参数近似为单个阻尼块单独敷设时的最佳厚度参数。

通过优化各阻尼块的敷设位置及厚度参数，使结构的第r阶模态损耗因子最大化的优化数学模型可表示为式(3)：

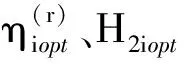
(3)

2 耗散率一致化优化

2.1 优化方法

Roux认为生物生长及进化的方向是用体积最小、质量最轻的结构来承受最大的外力或完成一定的功能[11]。结构优先生长承受最大载荷的地方，而承受较小载荷的地方得不到生长，最终得到强度均匀的结构。参考结构拓扑进化法[12]，采用多次“生长”的方式设计局部约束阻尼层，确保局部最佳参数趋近于整体最佳参数。

在原阻尼结构上，以耗散率为准则评价各阻尼块在生长时是“高效的”或“低效的”，优先在耗散率最大、获得最大模态损耗因子的位置“生长”，使各个阻尼块耗散率一致化，逐步增加约束阻尼层，重复以上步骤，直至附加阻尼结构质量满足设计要求，即是局部约束阻尼层耗散率一致化优化方法。

下面用反证法证明局部约束阻尼层耗散率一致化优化的可行性。

假设局部约束阻尼层阻尼块的总数为k，且各阻尼块的耗散率相等。

阻尼块的附加总质量为：

mt=m1+m2+…+mk

(4)

耗散率相等时，阻尼结构整体的模态损耗因子为：

(5)

将2号、k号阻尼块的质量分别减小、增大△m后，各阻尼块的耗散率不相等。

各阻尼块的附加总质量为：

mt=m1+(m2-△m)+…+(mk+△m)

(6)

耗散率不相等时，阻尼结构整体的模态损耗因子为：

(7)

由约束阻尼层的耗散率随质量的关系可知，在(m2-△m，m2)、(mk-△m，mk)生长阶段，2号阻尼块的耗散率大于k号阻尼块的耗散率。

可见，局部约束阻尼层各阻尼块耗散率不相等时的结构模态损耗因子较小。因此，本文所提耗散率一致化设计在理论上是可行的，可使局部约束阻尼层具有最佳的减振效果。

2.2 优化步骤

局部约束阻尼层耗散率一致化优化方法的流程图见图2，具体步骤如下：

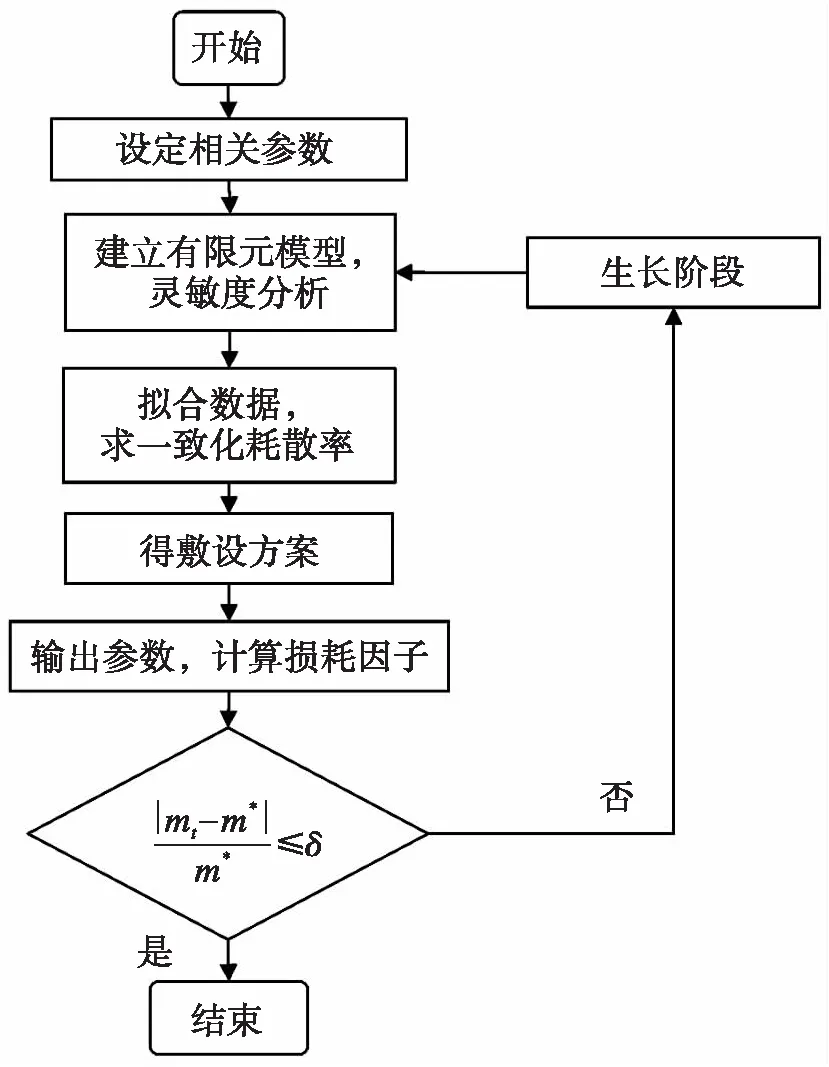
图2 局部约束阻尼层耗散率一致化优化流程Fig.2 The optimization flow chart of partial CLDdissipation rate unification

(1)建立局部约束阻尼层结构的有限元模型；

(2)设定附加阻尼结构质量、生长阶段数、各个生长阶段生长步长；

(3)按式(2)，采用模态应变能法及全局差分法，分析指定生长阶段内各个阻尼块单独敷设时耗散率对质量的灵敏度，同时得各个阻尼块的最佳厚度参数及其质量的关系；

(4)采用多项式函数拟合步骤(3)所得数据点，得质量、耗散率、最佳厚度参数之间的函数关系；

(5)定义初始的一致化耗散率，根据步骤(4)中耗散率与质量的关系，通过逐渐减小或增大一致化耗散率，得到满足单个生长步长的质量要求、各阻尼块一致化的耗散率；

(6)如果某阻尼块的耗散率小于一致化的耗散率，则说明此阻尼块是“低效”的，不应在该位置敷设阻尼块，从而实现对局部约束阻尼层敷设位置的优化；

(7)根据步骤(4)的函数关系，得所选敷设位置上各阻尼块的质量及最佳厚度参数，实现对各个阻尼块厚度参数的优化；

(8)按设计结果敷设约束阻尼层，计算结构损耗因子；

(9)判断是否满足附加阻尼结构质量约束条件。如果不满足约束条件，重复步骤(3)～(8)继续“生长”；如果满足约束条件，则结束。

3 算例

3.1 有限元模型

板结构是阻尼减振应用对象的基本结构形式。通过研究约束阻尼板的振动特性，可为具体设备的减振工程提供参考。本文以基层四边简支的阻尼板为研究对象。

板长360 mm，宽270 mm，厚1 mm.基层和约束层的材料均为铝材，弹性模量68.9 GPa，泊松比0.33，密度2740 kg/m3，忽略损耗因子；阻尼材料为橡胶，弹性模量44 MPa，泊松比0.495，密度999 kg/m3，损耗因子0.88.

按6×6将板均匀分隔为36块，采用Solid185单元并打开增强应变及混合模式以模拟橡胶材料，采用多点约束模拟层间接触[13]。为确保约束阻尼层的工艺性，阻尼层和约束层最小厚度分别定为0.2 mm、0.1 mm.局部约束阻尼板模型见图3.

3.2 不同质量时约束阻尼层的一致化优化

以四分之一模型上的阻尼块为设计对象，其他位置按对称性设计。以约束阻尼板的第一阶模态为被控模态。各个生长阶段步长均为0.01 kg.采用局部约束阻尼层耗散率一致化优化方法，得到不同附加阻尼质量的局部约束阻尼层的敷设位置及各个阻尼块的质量如表1所示。局部约束阻尼层的减振效果见图4.

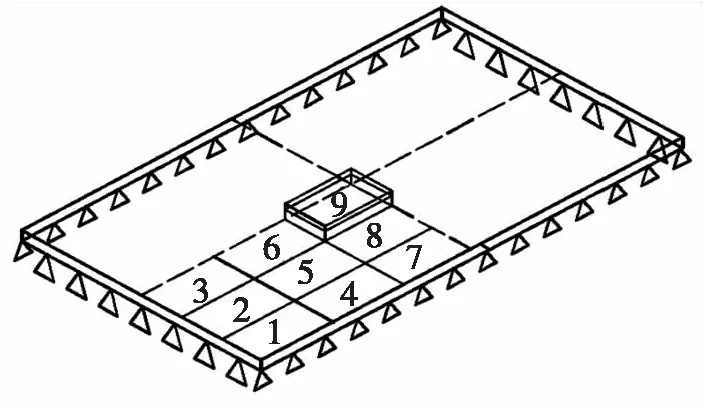
图3 局部约束阻尼板模型Fig.3 Model of partial constrained damping plate

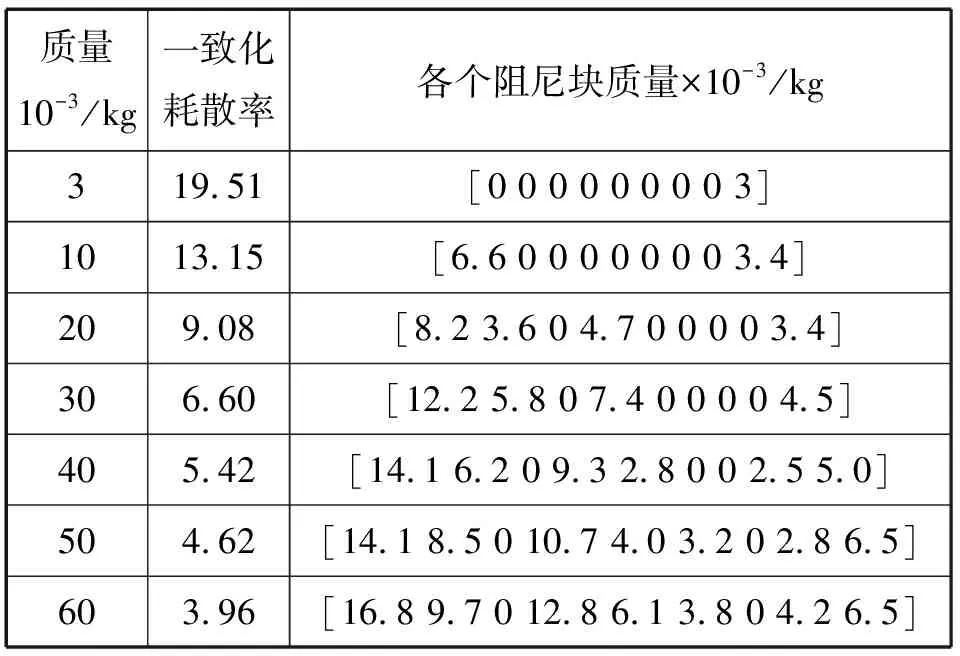
表1 不同质量时的耗散率一致化优化结果Tab.1 Results of dissipation rate unification optimizationof CLDs with different weights

由表1可见，局部约束阻尼层附加阻尼质量不同时，阻尼块的敷设位置及其质量不同。具体分析如下：

(1)随着局部约束阻尼层附加阻尼质量的增大，结构的模态损耗因子从质量为0.003 kg时的0.050，逐渐增大，质量为0.06 kg时为0.458，而增速如图3所示，呈逐渐放缓趋势，同文献[10]一致；一致化的耗散率从质量为0.003 kg时的19.51，逐渐降低，质量为0.06 kg时仅为3.96.可见，附加阻尼质量越大，单位质量阻尼层的减振效果越差，材料利用率相对较低。因此，在满足减振要求的前提下，应避免在结构上敷设过多的约束阻尼层。

(2)随着附加阻尼质量从0.003 kg增大至0.06 kg，局部约束阻尼层的最佳敷设位置从质量为0.003 kg时的9号位，逐渐扩展至质量为0.06 kg时的1、2、4、5、6、8及9号位， 而且可以预测如果附加阻尼质量继续增大，所有位置均为最佳位置。基层第一阶模态应变能密度如图5所示。1、9号位的应变能密度较高，而3、7号位的应变能密度较低。可见，随着附加阻尼质量的增大，局部约束阻尼层的敷设位置从应变能密度较高区域向较低区域扩展，敷设面积随之增大。

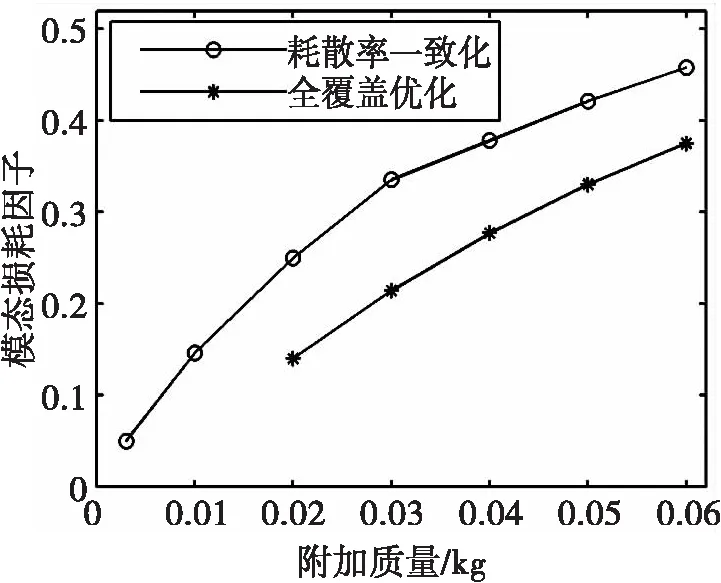
图4 不同优化方法的效果Fig.4 The effects of different optimization methods

(3)单个阻尼块的质量基本上是随着附加阻尼质量的增大而增大的，而且应变能密度越大，阻尼块质量也越大，但二者并不是成正比例关系，原因是附加阻尼改变了基层模态应变能密度分布。

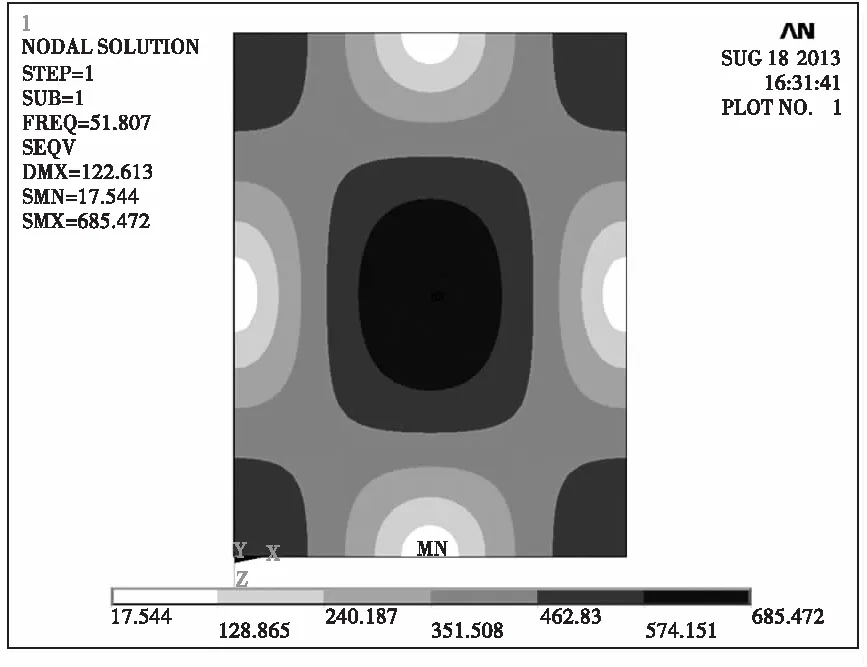
图5 应变能密度分布情况Fig.5 The reflection of strain energy density

作为对比，采用同样的约束阻尼板有限元模型，对全覆盖约束阻尼层的厚度参数进行优化，得全覆盖约束阻尼层的最佳厚度参数，其减振效果见图4.

由图4可见，相比全覆盖优化，耗散率一致化优化的局部约束阻尼层的模态损耗因子在不同质量下均得到了不同程度的提高，具有更好的减振效果。质量为0.003 kg、0.01 kg时，无法实现约束阻尼层全覆盖敷设。质量为0.02 kg时，耗散率一致化阻尼层的模态损耗因子提高了78.5%；而质量为0.06 kg时，模态损耗因子提高了22.0%.可见，约束阻尼层的质量越小，耗散率一致化优化效果更好。原因是质量较大时，约束阻尼层全覆盖优化与耗散率一致化优化的敷设位置大体相同，而且阻尼块自身耗散率较低，对厚度参数不敏感。因此，耗散率一致化优化可实现敷设位置和厚度参数的优化，且非常适用于质量较小的阻尼层设计。

3.3 不同生长方式对损耗因子的影响

为讨论不同生长方式对约束阻尼板模态损耗因子的影响，设计质量为0.06 kg时，采用相同的生长步长，得不同生长段数时，约束阻尼板模态损耗因子如图6所示；设计质量为0.06 kg时，生长段数为2，单个生长步长不同时的约束阻尼层模态损耗因子如图7所示。

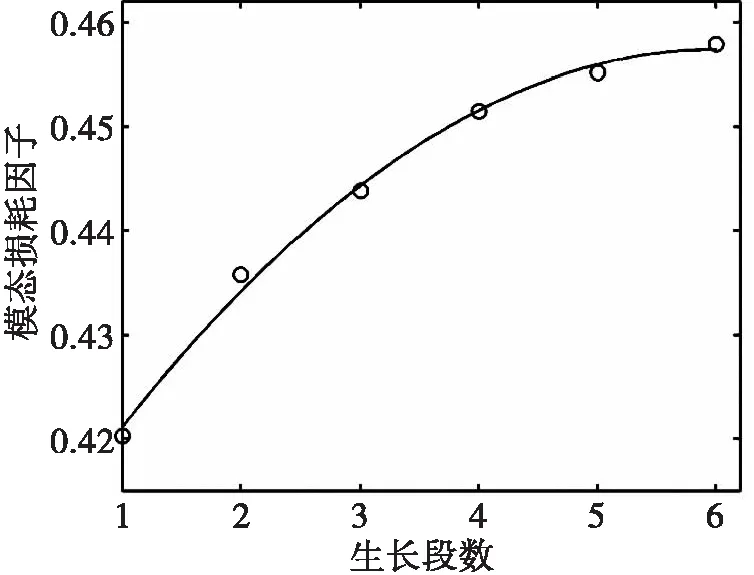
图6 生长段数对模态损耗因子的影响Fig.6 The effect of different growth times onmodal loss factor

由图6可见，约束阻尼板模态损耗因子随着生长段数的增多而增大，而增速逐渐降低。原因是，设计质量一定时，生长段数越多，步长越小，增加的约束阻尼层对基层的动力学影响小，单个约束阻尼块的最佳设计趋近于整体敷设时的最佳设计，优化效果越好。生长段数已较大时，单步增加的质量极小，不同生长段数的设计结果基本无差异，增加生长段数已没有意义。因此，在满足计算精度下，应取较小的生长步长，但不应过分追求小步长。

由图7可见，随着第1步步长的增大，约束阻尼板模态损耗因子先增大，后减小存在最佳值。原因是，整个约束阻尼层各阻尼块的耗散率由最后一步的生长过程决定。最后一步的生长步长越小，单个约束阻尼块的最佳设计越趋近于整体敷设时的最佳设计。第1步生长步长为0.05 kg时，第一步步长过大，各阻尼块的耗散率已经较为分散；最后一步进化步长虽小，但仍不能使耗散率一致，约束阻尼板模态损耗因子并不是最大。因此，应用时，应将取若干不同的生长步长，先按较大步长开始生长，后按较小步长生长。

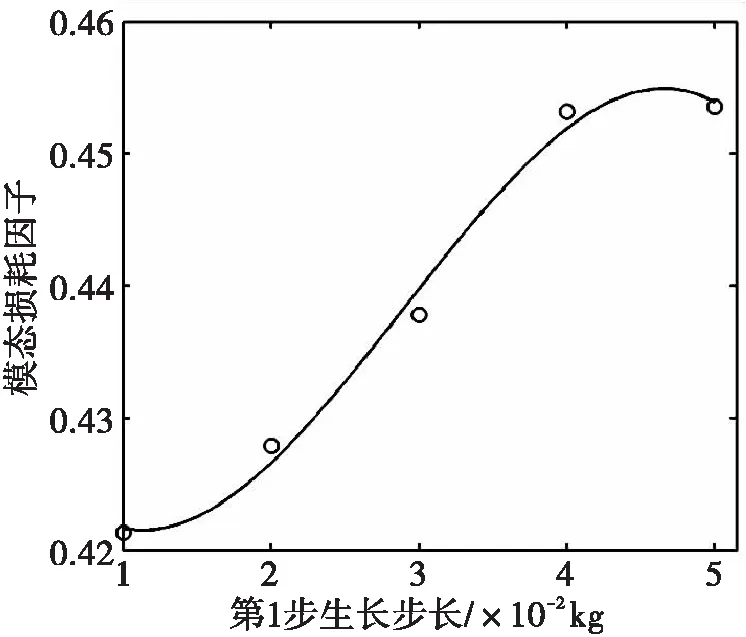
图7 生长步长对模态损耗因子的影响Fig.7 The effect of different growth step sizes onmodal loss factor

4 结论

(1)局部约束阻尼层耗散率一致化优化方法是可行的，可同时对敷设位置和厚度参数进行优化，能显著提高约束阻尼层的减振效果，可用于减振工程中局部约束阻尼层的设计及其优化。

(2)局部约束阻尼层的质量约束条件不同，其敷设位置及各阻尼块质量不同，且质量越大，敷设面积越大，敷设位置从应变能密度最大处逐渐扩展至应变能密度较小的区域。同时，应变能密度越大，阻尼块质量相应越大。

(3)适当的生长段数及合理的生长顺序既能保证优化结果的准确性，又能减少计算量，可采用先大步长、后小步长的两段式生长方式。

参考文献：

[1]ARAUJO A L，MARTINS P，SOARES C M，et al.Damping optimization of viscoelastic laminated sandwich composite structures[J].Structural and Multidisciplinary Optimization，2009，39(6)：569-579.

[2]SUBRAMANIAN S，SURAMPUDI R，THOMSON K R，et al.Optimization of damping treatment for structure borne noise reduction[J].SAE transactions，2003，112(6)：1926-1938.

[3]郑玲，谢熔炉，王宜，等.基于优化准则的约束阻尼材料优化配置[J].振动与冲击，2010，29(11)：156-159，259.

[4]王明旭，陈国平.基于变密度方法约束阻尼层动力学性能优化[J].南京航空航天大学学报，2010，42(3)：283-287.

[5]郭中泽，陈裕泽，侯强，等.阻尼材料布局优化研究[J].兵工学报，2007，28(5)：638-640.

[6]ALVELID M.Optimal position and shape of applied damping material[J].Journal of Sound and Vibration，2008，310(4)：947-965.

[7]CHIA C M，RONGONG J A，WORDEN K.Strategies for using cellular automata to locate constrained layer damping on vibrating structures[J].Journal of Sound and Vibration，2009，319(1)：119-139.

[8]杨加明，张义长，吴丽娟.多层黏弹性复合材料结构阻尼性能优化设计[J].航空学报，2011，32(2)：265-270.

[9]JOHNSON C D.Design of passive damping systems[J].Transactions-American Society of Mechanical Engineers Journal of Mechanical Design，1995，117：171-171.

[10]黄彩虹，曾京.基于约束阻尼层的高速客车车体弯曲振动的抑制[J].交通运输工程学报，2010，10(1)：36-42.

[11]王远亮，唐丽灵，王建华，等.成骨细胞响应机械刺激的力化学转导机理[J].生物医学工程学杂志，2005，22(2)：400-402.

[12]XIE Y M，STEVEN G P.Basic Evolutionary Structural Optimization[M].Springer London，1997.

[13]杨靖波，华旭刚，陈政清，等.约束阻尼层在输电塔风振控制中的应用[J].振动工程学报，2010，23(4)：389-396.