交通瓶颈处大、小型车插队行为的演化分析

杨紫洁，贾志绚

(太原科技大学，太原 030024)

交通瓶颈，广义上是指一切使道路通行能力受到限制的设施或路段，如交通信号灯，入口匝道，出口匝道，交叉路口，收费站，车辆限速，道路缩减以及上坡路等，稳定均匀的自由车流到达瓶颈处时会受到扰动，进而演化成不同特征的交通拥挤，阻碍着城市经济以及空间布局结构的良性发展[1]。在交通瓶颈处不规范的驾驶行为会导致交通拥堵情况更加严重，裴玉龙等构建了道路车辆不良汇入驾驶行为的模型，并运用纳什均衡分析了汇入行为发生的概率[2]；石京等分析了北京市机动车驾驶员的“抢行”即插队行为及其影响因素，表明不同的驾驶员群体产生“抢行”行为的概率不同[3]；李振龙，余孝军等运用博弈论研究了超速驾驶行为，构建了博弈模型并提出合理建议[4-5]。驾驶行为是反复博弈的动态过程，静态的均衡不能完全描述驾驶行为的演化过程，不同特征的驾驶员群体具有不同的心理特征。

本文分析了在交通瓶颈处驾驶员为个人收益最大化包括时间效益与拥堵成本而不按交通规则行驶，导致违规插队驾驶行为的产生过程，并应用演化博弈论[7-8]分析了在交通瓶颈处大、小型车驾驶员产生插队行为的不同心理博弈过程及排队与插队策略选择过程，研究驾驶行为稳定性及其演化趋势。

1 调查数据

本文调查了太原市窊流路路段中部与铁道交叉口处驾驶员插队驾驶行为，此处由于历史原因造成道路由双向六车道在铁轨处收窄为双向两车道，如图1、图2所示，驾驶员在瓶颈处排队或插队的决策过程。

图1 交通瓶颈处排队及插队驾驶行为Fig.1 Queuing and queue-jumping at traffic bottleneck

基于对调查点处高峰期6段15 min/段视频数据的统计分析，表1所示为瓶颈处插队行为的统计数据，其中大型车插队行为87次，占大型车交通量29%，小型车144次，占小型车交通量21%，并且大型车插队行为的比重都略大于小型车。从行为心理学上分析，大型车驾驶员有占优心理，认为自己车型大且相对于小型车而言价值较低，从而冒险插队行为增加；而小型车多属于私家车，驾驶员具有害怕碰撞和拥堵的心理，从而冒险插队行为相对较少，是典型的非对称博弈。大量的插队行为致使交通通行能力迅速下降，拥堵系数均小于1，车辆通过量远未达到一条车道的理论通行能力，说明车流处于低速运行状态，服务水平降低，驾驶员的行为对瓶颈处交通情况有很大的影响，对其进行分析研究是非常必要的。

图2 铁道交叉口处插队情况Fig.2 Queue-jumping at railway intersection

表1所示为大、小型车插队频次占其交通量百分比及拥堵系数值，其中拥堵系数的计算参考日本道路交通形势调查中交通畅通性的评价指标，公式如下：

γT=1-T+ET·T

(1)

(2)

式中：CC为拥堵系数；T为大型车辆混入率；ET为大型车辆的小客车当量系数(取ET=2.0)；Q为观测15 min交通量；C为评价基准15 min交通量(取C=1 730/4)，其中基准交通量1 730 pcu/h为《城市道路设计规范》建议的一条车道60 km/h时理论通行能力[6]。

表1 瓶颈处插队行为统计分析Tab.1 Statistical analysis of queue-jumping at bottleneck

2 模型构建

博弈论是一门研究理性决策主体之间合作及冲突的理论，在交通领域中常被应用于交通控制、拥挤定价、拥挤产生的机理及交通流分配等方面的研究。应用古典博弈论研究驾驶行为存在三方面不足：(1)传统博弈论分析驾驶行为往往不能达到所要求的完全理性，驾驶员的驾驶行为都是有限理性的；(2)以往博弈论的应用大部分是静态的均衡，然而驾驶行为是不断变化的动态博弈，不仅是驾驶员决策的先后发生，而应使得到的结果为动态均衡；(3)对驾驶行为进行博弈分析忽略了不同特征驾驶员的不同心理过程对驾驶行为的作用，故应区分驾驶员群体分析驾驶行为。为此，文中运用演化博弈论进行研究，在道路收窄处以有限理性为基础，强调动态过程，区分大型车驾驶员和小型车驾驶员不同心理过程，对驾驶员群体插队行为进行了分析。

2.1 演化博弈模型的建立

驾驶员在进入交通瓶颈处有两种策略选择：一种是排队，即按照标志线和道路交通法规进行排队。另一种是插队，即不按照标志线和道路交通法规进行排队而违规切入其他车道插队。

以大型车和小型车两类驾驶员不同心理特征区分研究插队驾驶行为，针对不同驾驶员群体长期进行排队或插队的博弈，建立大型车和小型车插队行为的非对称复制动态模型。

(1)假设m为交通监管力度系数且m>0，如果两驾驶员群体全部选择插队策略，得到支付u与其分别需要支付的博弈成本ai(i=1，2，a>0)成正比例关系。

(2)假设两驾驶员群体分别选择排队和插队策略时，那么选择插队策略的驾驶员支付不变，而选择排队的驾驶员支付为在第(1)种情况的基础上加上需为此付出的额外成本ci(ci>0).

(3)假设两驾驶员群体都选择排队策略时，则两驾驶员群体都会付出额外成本ci，但由于相互排队避让带来双赢的结果，μ为合作带来的增长因子，两驾驶员群体支付会得到μ倍的增加，。

按照上述定义得到如表2所示的演化分析博弈支付结果。

表2 博弈支付Tab.2 Game payoff

假设驾驶员1中，选择排队策略的比例为s1(0≤s1≤1)，则选择插队策略的比例为1-s1；同理，驾驶员2中选择排队策略的比例为s2(0≤s2≤1)，选择插队策略的比例为1-s2.

驾驶员1群体选择“排队”的期望支付为：

u11=[(1+μ)a1m-c1]s2+[a1m-c1](1-s2)=
μa1ms2+a1m-c1

(3)

选择“插队”时期望支付为：

u12=a1ms2+a1m(1-s2)=a1m

(4)

则驾驶员1群体得到期望支付为：

(5)

由此可得，系统的动态复制方程组为：

(6)

2.2 渐进稳定性分析

演化稳定策略(ESS)是演化博弈论中被用来描述动态系统局部的稳定性和在稳定状态下演进过程的一个概念。

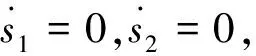
当detJ≠0时，雅可比矩阵J是非奇异的，且有唯一解。

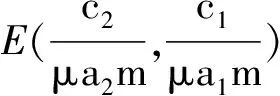
在双矩阵两种群演化博弈分析中，渐近稳定点为动态复制系统(6)的稳定演化策略，由此可得出结论：

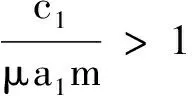
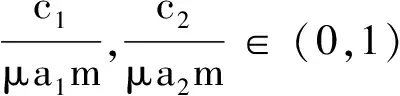
2.3 各参数对演化过程和结果的影响

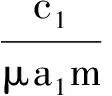
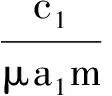
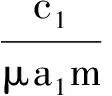
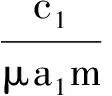
3 结论

运用演化博弈论对太原市某交通瓶颈处大、小型车插队行为进行动态分析，研究了大、小型车驾驶员群体插队行为的心理博弈过程，建立了驾驶员群体排队与插队的决策博弈模型。研究结果表明：大型车驾驶员和小型车驾驶员群体的博弈过程属于非对称性博弈，通过提高交通监管力度、增加排队的收益、提高驾驶员素质和减小排队支出的额外成本可使驾驶员群体采取稳定的排队策略，缓解交通拥堵。研究结论为交通管理者制定交通管理措施及制度提供了理论基础，为缓解交通瓶颈处的交通拥堵提供了新的思路和方法。

参考文献：

[1] 祝会兵.基于驾驶行为细致分析的交通流建模和模拟[D].上海：上海大学，2008.

[2] 裴玉龙，漆巍巍.道路车辆不良汇入驾驶行为的模型构建[J].交通信息与安全，2009，27(2)：29-31.

[3] 石京，陶立，白云，等.北京市机动车驾驶员“抢行”行为及影响因素分析[J].中国安全科学学报，2010，20(8)：30-39.

[4] 李振龙，张利国.超速驾驶行为的演化博弈[J].交通运输系统工程与信息，2010，10(4)：137-142.

[5] 余孝军.超速驾驶行为的进化博弈分析[J].数学的实践与认识，2009，39(11)：14-18.

[6] 王炜，过秀成.交通工程学[M].南京：东南大学出版社，2000.

[7] 王武宏，孙逢春，曹琦，等.道路交通系统中驾驶行为理论与方法[M].北京：科学出版社，2001.

[8] 雷霖，刘倩.现代企业经营决策——博弈论方法应用[M].北京：清华大学出版社，1999.

[9] 孙连菊.基于博弈论的城市公共交通系统建模与算法研究[D].北京：北京交通大学，2009.

[10] 邵祖峰.博弈论在道路交通管理中的应用[J].道路交通与安全，2006，6(3)：8-10.

[11] 张杰.博弈框架下的交通信号灯控制算法研究[D].北京：北京工业大学，2009.