一种基于知识距离的决策规则的评测
杨贵如
(阳泉师范高等专科学校,山西 阳泉 045200)
粒度计算(GrC)是信息处理的一种新的概念,主要研究的是模糊的、不完整的、不确定的和海量的信息。它的三大研究模型分别为基于模糊集合论的词计算模型、基于粗糙集理论的粒度计算模型和基于商空间的粒度计算模型,已经广泛应用于各个领域[1-3]。其中粗糙集模型中的论域粒化成为研究的热点之一。
1982年,Pawlak教授提出了粗糙集理论[4],作为一种处理不确定的、模糊的、和不完备性问题的新型数学工具,被国内外学者广泛的重视和发展[5-7]。其中决策规则性能的评测,是粗糙集的一大热点研究内容,通常采用确定度来衡量其性能。由于粒度计算这种新型的研究工具已经得到了广泛的应用,如何通过粒度计算来评测决策规则成为了新的研究问题。因此,本文基于粒度计算的思想,以知识距离为准则,提出了一种粒化的算法,通过粗化条件属性集,实现对决策规则的评测。实例证明该方法评测效果较为理想。
1 基本概念

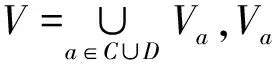
定义3[9]设S=(U,C∪D)是一个决策表,Xi∈U/C,Yj∈U/D,desC(Xi)是Xi在C下的唯一描述,desD(Yj)是Yj在D下的唯一描述。决策规则定义如下:
rij∶desC(Xi)→desD(Yj),Xi∩Yj≠Ø,决策规则rij的确定度μ(Xi,Yj)=|Xi∩Yj|/|Xi|,0<μ(Xi,Yj)≤1.
当μ(Xi,Yj)=1时,rij是确定的;当0<μ(Xi,Yj)<1时,rij是不确定的。
定义4[9]设有集合A和集合B,A和B的集合贴近度定义为:
其中0≤H(A,B)≤1.
定义5[9]设S=(U,A)是一个信息系统,P,Q⊆A,P和Q所对应的知识分别为:
U/SIM(P)={SP(x1),SP(x2),…,SP(x|U|)}和
U/SIM(Q)={SQ(x1),SQ(x2),…,SQ(x|U|)}
则知识U/SIM(P)和知识U/SIM(Q)的知识贴近度定义为:
定义6[9]设有集合A和集合B,A和B的集合差异度可以定义为:
定义7[9]设S=(U,A)是一个信息系统,P,Q⊆A,P和Q所对应的知识分别为:
U/SIM(P)={SP(x1),SP(x2),…,SP(x|U|)}和
U/SIM(Q)={SQ(x1),SQ(x2),…,SQ(x|U|)}
则知识U/SIM(P)和知识U/SIM(Q)的知识距离定义为:
2 决策规则的评测
下面通过例1来说明决策规则的评测标准。
例1关于诊断感冒的决策表S=(U,C∪D)如下表1,其中U={x1,x2,x3,x4,x5,x6,x7,x8},C={a1,a2,a3}={头疼,肌肉疼,体温},D={d}={感冒}。
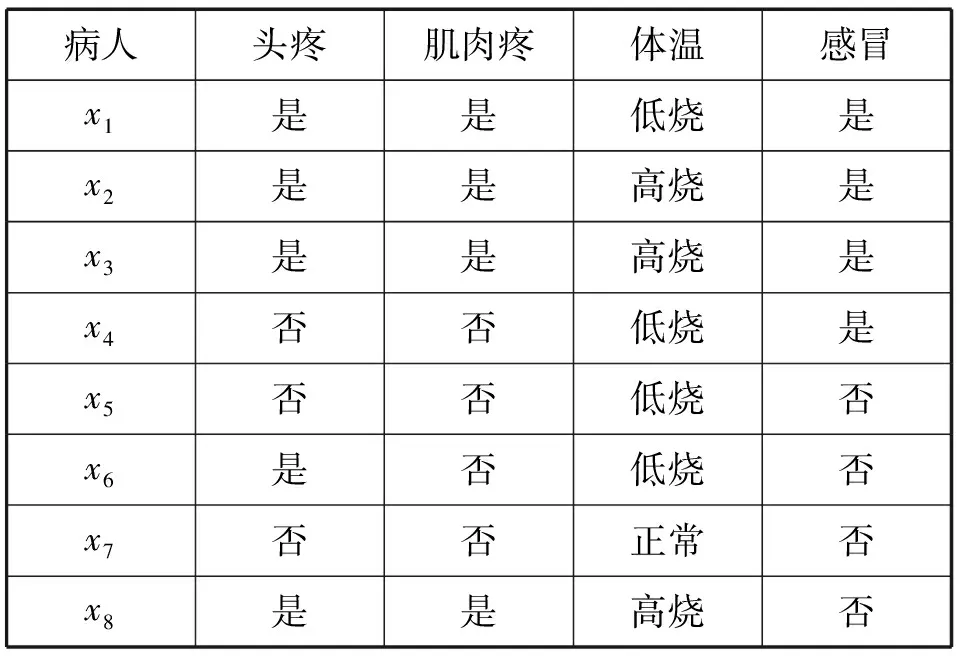
表1 诊断感冒的决策表Tab.1 The decision table in the diagnosis of a cold
根据表1得:
U/C={X1,X2,X3,X4,X5}={{x1},{x2,x3,x8},{x4,x5},{x6},{x7}};
U/D={Y1,Y2}={{x1,x2,x3,x4},{x5,x6,x7,x8}};
r11∶desC(X1)→desD(Y1),μ(X1,Y1)=1;
r42∶desC(X4)→desD(Y2),μ(X4,Y2)=1;
r52∶desC(X5)→desD(Y2),μ(X5,Y2)=1;
如对新对象x9(头疼=是,肌肉疼=是,体温=高烧)进行分类时,根据上述规则,适用的规则是r21和r22,由于μ(X2,Y1)>μ(X2,Y2),则认为x9属于Y1的可能性较大。
如对新对象x10(头疼=否,肌肉疼=否,体温=低烧)进行分类,适用的规则是r31和r32,由于μ(X3,Y1)=μ(X3,Y2),此时无法就x10的归属做出决策。因此,本文运用知识距离,提出了一种基于粒度计算的评测方法,能够较好的解决上述问题。
3 决策规则的评测算法
针对上述问题可以看出,当条件属性集以整体的形式来评测决策规则时,制约评测结果的因素过多过细,使得无法对规则作出较为准确的评测。为此,可以适当的将制约的条件删减一些,即粗化条件属性集,这样不仅充分考虑了确定性在粗化条件属性集上的差异,还能较理想的对规则作出评测。
根据粒度计算的思想,提出了一种粒化算法,该算法以知识距离为准则,通过粗化条件属性集,对决策规则进行评测。算法的步骤如下:
输入:信息系统S=(U,C∪D)
输出:S的粒化S′=(U,C′∪D)
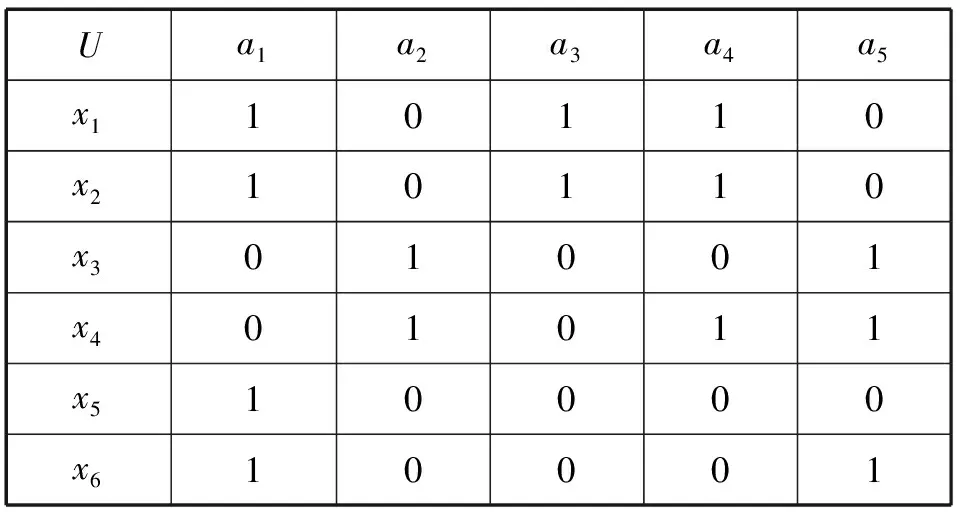
Step1:计算U/C={Xi}i=m,0 Step2:若存在Xi→Y1,Xi→Y2,…,Xi→Yn,其中Xi∈{Xi}i=m,0 Step3:计算知识距离D(C,{cl}),cl∈C,l=1,2,…,|C|.找出最大的D(C,{cl})值及其对应的属性c,并将属性c从条件属性集C中删除,得到粒化的条件属性集C′; Step4:根据新的条件属性集C′,得到了S的粒化S′=(U,C′∪D).并重新计算U/C′={Xk}k=r,0 算法分析: 首先执行Step1和 Step2,将条件属性集作为一个整体去评测,如果能够作出评测,则表明在最细粒度下可以进行决策规则的评测。如果不能评测,则执行Step3,以知识距离为准则,计算单个条件属性和条件属性集这两个知识的知识距离,从中删减掉知识距离最大的属性,实现了将条件属性集粗粒化的效果。根据得到的粗粒化信息系统S′,求出相应的规则和确定度,以新的确定度对决策规则进行评测。若粗化后的信息系统对决策规则还是无法进行评测,则实行再次粗化,直至能够对决策规则进行评测为止。 以例1为例,对新对象x10(头疼=否,肌肉疼=否,体温=低烧),采用知识距离粒化的算法进行分类。 (1)计算U/C={X1,X2,X3,X4,X5}={{x1},{x2,x3,x8},{x4,x5},{x6},{x7}},U/D={Y1,Y2}={{x1,x2,x3,x4},{x5,x6,x7,x8}},在例1中,对x10的分类适用的规则为r31和r32,并且μ(X3,Y1)=μ(X3,Y2). (2)根据知识距离的定义可得: U/SIM(C)={{x1},{x2,x3,x8},{x2,x3,x8},{x4,x5},{x4,x5},{x6},{x7},{x2,x3,x8}} U/SIM({a1})={{x1,x2,x3,x6,x8},{x1,x2,x3,x6,x8},{x1,x2,x3,x6,x8},{x4,x5,x7},{x4,x5,x7},{x1,x2,x3,x6,x8},{x4,x5,x7},{x1,x2,x3,x6,x8}} U/SIM({a2})={{x1,x2,x3,x8},{x1,x2,x3,x8},{x1,x2,x3,x8},{x4,x5,x6,x7},{x4,x5,x6,x7},{x4,x5,x6,x7},{x4,x5,x6,x7},{x1,x2,x3,x8}} U/SIM({a3})={{x1,x4,x5,x6},{x2,x3,x8},{x2,x3,x8},{x1,x4,x5,x6},{x1,x4,x5,x6},{x1,x4,x5,x6},{x7},{x2,x3,x8}} (4)计算,U/C′={X1,X2,X3,X4}={{x1},{x2,x3,x8},{x4,x5,x6},{x7}},U/D={Y1,Y2}={{x1,x2,x3,x4},{x5,x6,x7,x8}} r11′∶dexC(X1)→desD(Y1),μ(X1,Y1)=1; r42′∶dexC(X4)→desD(Y2),μ(X4,Y2)=1. (5)根据粒化条件属性集的结果,对新对象x10评测的过程为: 适用的规则是r31′和r32′,由于μ(X3,Y2)>μ(X3,Y1),所以x10属于Y2的可能性大于Y1. 为了证明算法的可行性,另外列举了一个例子作说明。 例2为一个知识管理的决策表S=(U,C∪D)如表2,其中,U={x1,x2,x3,x4,x5,x6},C={a1,a2,a3,a4},D={a5}. 根据表1得: U/C={X1,X2,X3,X4}={{x1,x2},{x3},{x4},{x5,x6}} U/D={Y1,Y2}={{x1,x2,x5},{x3,x4,x6}} r11∶desC(X1)→desD(Y1),μ(X1,Y1)=1; r22∶desC(X2)→desD(Y2),μ(X2,Y2)=1; r32∶desC(X3)→desD(Y2),μ(X3,Y2)=1; 表2 知识管理的决策表Tab.2 The decision table of knowledge management 如对新对象x7(1,0,0,0)进行分类,适用的规则是r41和r42,由于μ(X4,Y1)=μ(X4,Y2),无法就x7的归属做出决策。因此,我们通过执行算法来解决x7的归属问题。 (1)根据知识距离的定义可得: U/SIM(C)={{x1,x2},{x1,x2},{x3},{x4},{x5,x6},{x5,x6}}; U/SIM({a1})={{x1,x2,x5,x6},{x1,x2,x5,x6},{x3,x4},{x3,x4},{x1,x2,x5,x6},{x1,x2,x5,x6}} U/SIM({a2})={{x1,x2,x5,x6},{x1,x2,x5,x6},{x3,x4},{x3,x4},{x1,x2,x5,x6},{x1,x2,x5,x6}} U/SIM({a3})={{x1,x2},{x1,x2},{x3,x4,x5,x6},{x3,x4,x5,x6},{x3,x4,x5,x6},{x3,x4,x5,x6}} U/SIM({a4})={{x1,x2,x4},{x1,x2,x4},{x3,x5,x6},{x1,x2,x4},{x3,x5,x5},{x3,x5,x6}} (2)由D(C,{a1})=D(C,{a2})=1=0.5可知,a1,a2为知识距离最大的属性,故删除a1,a2得到了粒化后的新的条件属性集C′={a3,a4}. (3)计算U/C′={X1,X2,X3}={{x1,x2},{x3,x5,x6},{x4}},U/D={Y1,Y2}={{x1,x2,x5},{x3,x4,x6}} r11′∶desC(X1)→desD(Y1),μ(X1,Y1)=1; r32′∶desC(X3)→desD(Y2),μ(X3,Y2)=1. (4)根据粒化条件属性集的结果,对新对象x7评测的过程为: 适用的规则是r21′和r22′,由于μ(X2,Y2)>μ(X2,Y1),所以x7属于Y2的可能性大于Y1. 提出一种基于粒度计算思想的算法,根据知识距离实现对条件属性集的粗化,通过此算法可以较好的解决决策规则的评测问题。实例表明该算法评测效果比较理想。 参考文献: [1] 张铃,张钹.模糊商空间理论(模糊粒度计算方法)[J].软件学报,2003,14(4):770-776. [2] 王飞跃.词计算和语言动力学系统的计算理论框架[J].模式识别与人工智能,2001,14(4):377-384. [3] 李士勇.模糊控制·神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998. [4] PAWLAK Z.Rough Sets-Theoretical Aspects of Reasoning about Data[M].Dordrecht,Boston,London:Kluwer Academic Publishers,1991. [5] 张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001. [6] LIANG J Y,SHI Z Z,LI D Y,et al.Information entropy,rough entropy and knowledge granulation in incomplete information systems[J].International Journal of General Systems,2006,35(6):641-654. [7] 曲开社,翟岩慧,梁吉业,等.形式概念分析对粗糙集理论的表示及扩展[J].软件学报,2007,18(9):2174-2182. [8] 李道国,苗夺谦,张红云.粒度计算的理论、模型与方法[J].复旦学报,2004,43(5):837-841. [9] 史琨.粗糙集的知识获取方法研究[D].太原:山西大学,2009.4 实例分析
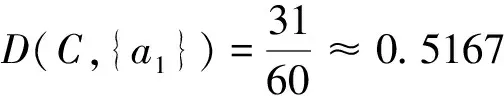
5 结束语

