基于静态有向种群结构的EPSO算法研究

台亚丽，曾建潮，莫思敏

(太原科技大学复杂系统与计算智能实验室，太原 030024)

为提高微粒群算法(PSO)[1]的性能，文献[2]提出了一种基于拟态物理学引斥力思想的扩展微粒群算法(EPSO)[2]。该算法重新构造了微粒间的信息交互和作用方式，使每个微粒获得更加全面的的搜索信息，因此其具有较快的收敛速度和较高的种群多样性，进而提高了算法的全局性能。但是，对于一些测试函数，EPSO算法具有较弱的局部搜索能力。为了提高EPSO的算法性能，文献[3]构造了不同的无向自组织种群拓扑结构[3]。然而在无向自组织种群结构中，相邻微粒之间的影响是对等的，这样就会存在被动连接的微粒被动地做全局搜索，从而减弱了EPSO算法的局部搜索能力。

EPSO算法是通过模拟生物社会群体行为而构造的一个新颖的算法。如果使EPSO算法不仅模拟生物社会群体行为，而且模拟生物社会网络结构，将能更加真实模拟生物社会，涌现更多的复杂行为，进而提高EPSO算法的性能。而在自然界和社会中存在大量的有向网络，它们广泛存在于社会、信息、科技、生物等领域，因此将有向的种群结构作用于EPSO上，使得微粒之间的交互作用关系体现出有向性，对提高EPSO算法性能是非常重要和必要的。

目前，基于有向种群结构的群智能算法研究较少。这些研究主要集中在：(1)理论上对有向网络中节点的分布问题和基本理论进行了综述和拓展，为我们对有向网络的研究提供了坚实的理论基础[4-5]；(2)为体现有向网络中粒子之间影响的不平衡性构造了有向加权函数模型[6]；(3)提出动态有向拓扑结构，模拟现实复杂网络中增长有向网络演化模型构造有向种群结构，并对有向网络演化过程中的度分布进行分析[7-8]，以及构造邻域动态变化的有向拓扑结构[9-10]，以提高微粒群在空间上的寻优能力。

由于EPSO算法是最近提出的一个新颖的算法，因此尚无文献研究EPSO算法的有向种群结构。本文针对EPSO算法的特点以及其在无向自组织种群结构研究中存在的不足，设计了各种静态有向种群结构，研究有向静态结构的特征度量对EPSO算法性能的影响，以获得有利于EPSO算法进化、提高EPSO算法性能的有向种群结构及特征度量。

1 EPSO算法

扩展微粒群算法(EPSO)是在标准微粒群算法(PSO)的基础上，将微粒仅受自身历史最好和种群历史最好的影响，扩展为微粒受种群中所有微粒历史最好的影响。并根据拟态物理学中引斥力思想，重新构造了微粒间的作用方式，将PSO中微粒仅受其他微粒吸引的作用方式，扩展为微粒受比自身适应值优的微粒的吸引，同时受比自身适应值劣的微粒的排斥，在引斥力的合力的作用下进行速度和位置的更新[2]。

微粒间引斥力规则定义为：

微粒j吸引微粒i：pjk(t)-xik(t)，集合B(i)存放历史最优适应值比微粒i适应值优的微粒。

微粒j排斥微粒i：-(pjk(t)-xik(t))，集合W(i)存放历史最优适应值比微粒i适应值劣的微粒。

其中：集合B(i)和W(i)的元素个数分别被表示为|B(i)|和|W(i)|.EPSO的速度和位置更新方程为：

(1)

xik(t+1)=xik(t)+vik(t+1)

(2)

其中：Pi={pi1,pi2,…,pin}代表微粒i所经历过的最好位置，Xi(t)={xi1(t),xi2(t),…,xin(t)}和Vi(t)={vi1(t),vi2(t),…,vin(t)}分别是第t代微粒i的位置和速度矢量，w为惯性权重，用来平衡算法的全局搜索和局部搜索，在区间[0，1]上取值，cj(j=1，…，N)是加速系数，rj是在[0，1]均匀分布的相互独立的随机数。

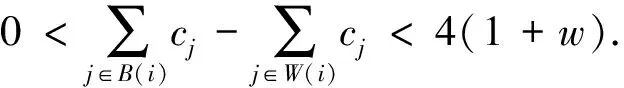
2 静态有向种群结构的特征度量对EPSO算法性能的影响

从收敛条件可知加速系数c和微粒的邻居数量对微粒的收敛性起到重要的作用，因此EPSO算法性能受节点度和结构的度分布的影响较大[3]。而在有向种群结构中，考虑到连接有向边的两节点的受力情况不同，因此有向结构中节点的出度和入度的变化是影响信息传播和EPSO算法性能的重要因素。其次，随着EPSO算法的进化，微粒的适应值不断地发生变化，连接两微粒的有向边可能无助于微粒的进化，需要重新选择对象建立有向边，因此在建立有向种群结构中应考虑适应值对算法性能的影响。

2.1 节点出度值对算法性能的影响

在有向结构中，有向边以节点u为起点的边的数目称为u的出度，以节点u为终点的边的数目称为u的入度。

为了研究有向种群结构中节点的出度对EPSO算法性能的影响，本节在环形有向结构(如图1(a))的基础上分别对结构中的每个节点i引kout条出度边，这些边分别指向编号为i+2，i+3，…，i+kout-1，i+kout的节点(如图1(b))，通过调整kout值来改变节点i的出度值。

实验环境为：种群规模与函数维数相等，即N=n=30，惯性权重w从0.9到0.4线性递减，最大进化代数为20 000.表1记录了算法独立运行30次各个测试函数的平均值和方差。

从表1可以看出：(1)节点出度较小时的算法性能优于出度较大时的算法性能；(2)对于全局最优点在(1，1…，1)点的函数，有向结构中节点的出度值较小，且加速系数c值也较小时，EPSO算法的性能较优；(3)对于全局最优点在(0，0…，0)点的函数，当有向结构中节点的出度值较小，加速系数c值较大时，EPSO算法的性能较优；(4)对于所有的测试函数，在节点的出度较大(kout>5)的情况下，c值较大时的算法性能优于c值较小时的算法性能。

在环形有向结构中，当节点的出度较小时，每个微粒受相邻较少微粒的作用，在较小的c值下，微粒在每一维上所受的合力较小，有效提高了EPSO算法的局部搜索能力，当c值较大时，微粒所受的合力较大， 算法具有较强的全局搜索能力。 当节点的出度增加时，每个微粒受到较多微粒的作用，在较小的c值下，出度值大的节点对应的微粒仅在很小的邻域内进行搜索，因而影响算法的收敛速度，而在较大的c值下，微粒受到较大的合力作用，以相对较大的速度进行全局搜索，算法的全局搜索能力较强。

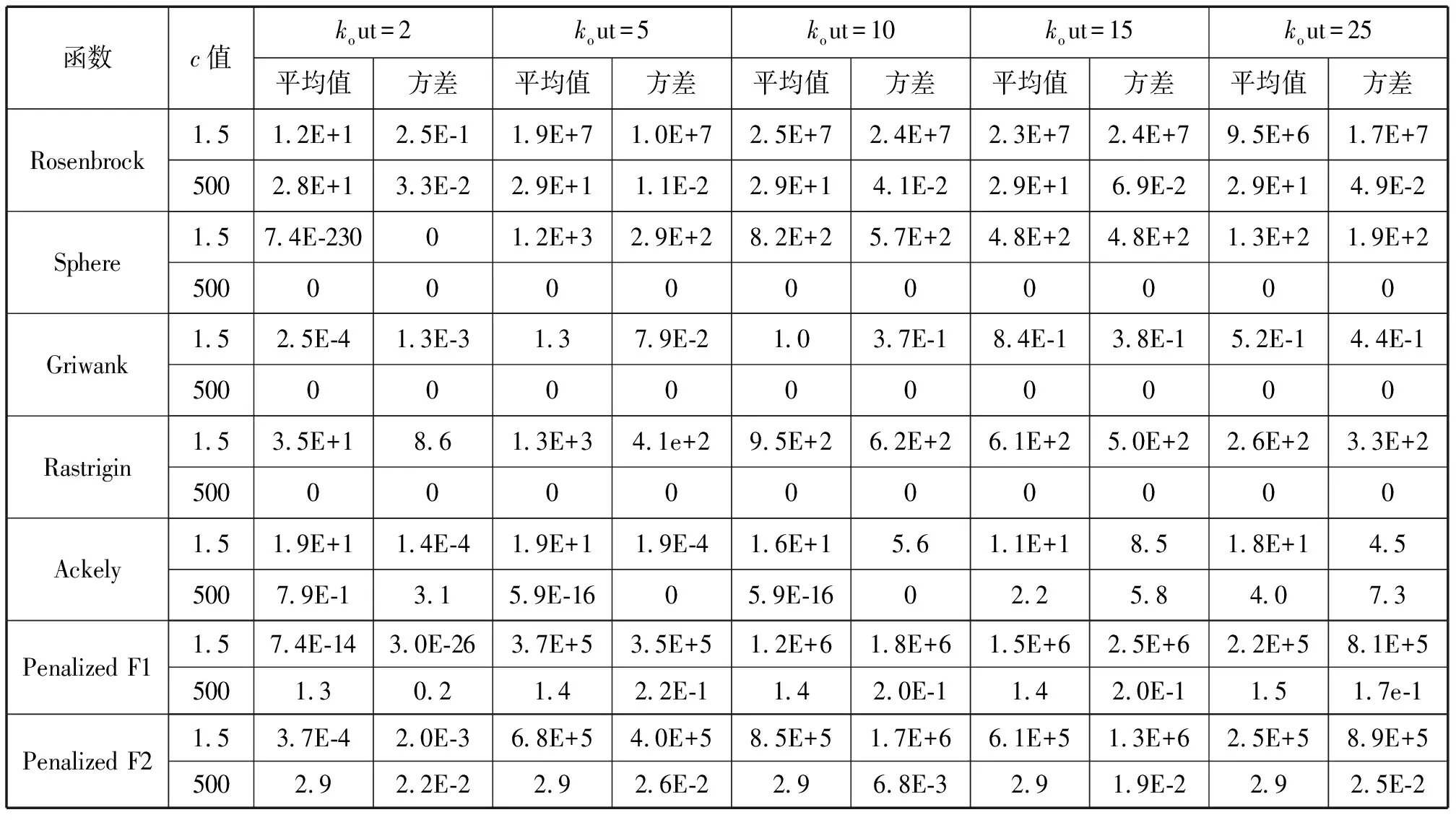
表1 环形有向结构不同出度下的EPSO性能Tab.1 Performances of EPSO at the ring-like directed structure with different outdegrees

2.2 节点入度值与适应值对算法性能的影响

(1)理论上，随着EPSO算法的进化，当连接有向边的微粒的适应值发生改变时，微粒都希望以较大的概率与适应值较好的微粒相连接，以受到群体中适应值较好微粒的力的作用。因此本节研究在初始结构是环形的有向结构中，节点的出度值保持不变，通过改变适应值较优节点的入度值来研究入度值与适应值对算法性能的影响。实验环境为：种群规模N=10，函数维数n=30，w从0.9到0.4线性递减，最大进化代数为2 000.图2以Sphere函数为例记录了算法运行过程中十个节点向最优值靠近的情况。图3则记录了以Rosenbrock函数为例，种群规模与函数维数相等，即N=n=30，最大进化代数为20 000时与EPSO算法的微粒平均适应值的变化对比。

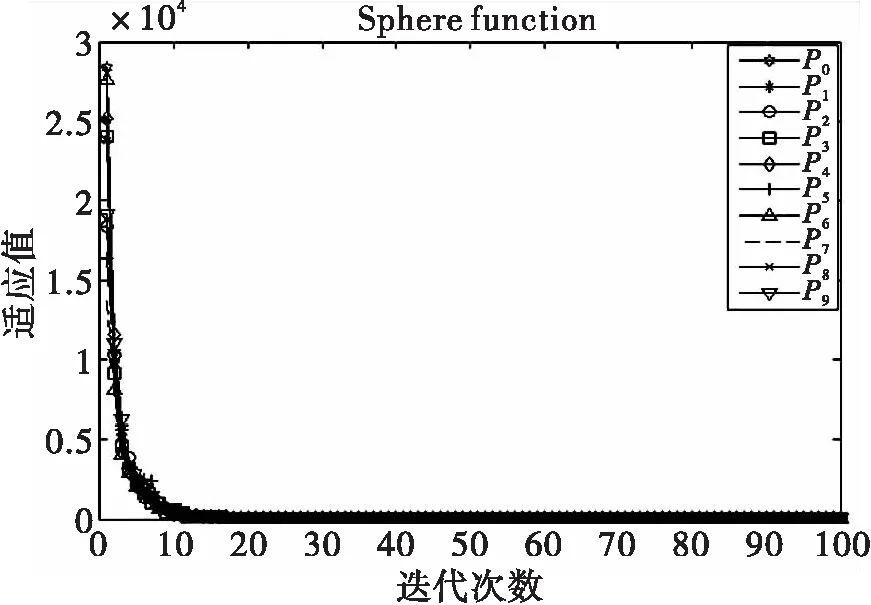
注：点所对应的迭代次数为横坐标刻度的20倍图2 节点出度不变而较优节点入度增加时微粒适应值的变化Fig.2 Fitness evolution in directed structure when outdegree of nodes is fixed，and indegree of the better particles increases

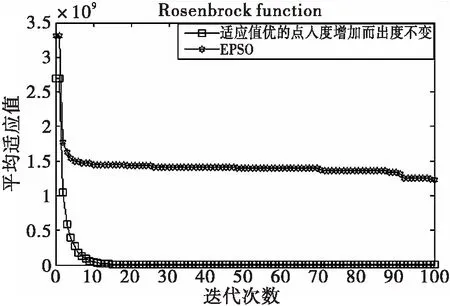
注：点所对应的迭代次数为横坐标刻度的200倍图3 出度不变较优节点入度增加与EPSO平均适应值比较Fig.3 Comparison of EPSO average fitness evolution indirected structure when outdegree is fixed, and indegreeof the better particles increases

从图中可看出，当种群中节点的出度值不变而适应值好的节点的入度值增加时，微粒都以较快的速度向最优值聚集，并且相对于EPSO算法，其平均动态性能较好。这是由于在有向种群结构中，有向边起点微粒受终点微粒的力作用，而终点微粒不受起点微粒的力作用，因此随着算法进化，微粒断开与适应值变差的微粒的连接，受到适应值好的微粒的力的作用时，能大大提高EPSO算法的性能。

(2)为了研究有向结构中节点的适应值对EPSO算法性能的影响，构建星形的特殊有向结构如图4.以10个微粒(P0，P1，…，P9)的种群规模为例，其中微粒P1至P9仅与P0连接，且方向都指向P0，选择30维的Sphere函数进行实验，w从0.9到0.4线性递减，最大迭代次数均为500.

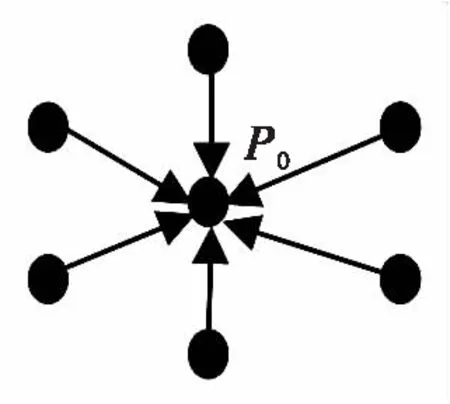
图4 星形有向结构(中心点为P0)Fig.4 Star-like directed structure (center point is P0)

(a)首先研究当星形结构中心点微粒P0不固定时，十个微粒的适应值的变化情况。由图5可以看出，在星形有向结构中，当中心点微粒不固定时，种群呈现出非常好的多样性，但是群体微粒的聚集性较差，所以该结构下EPSO算法的具有较强的全局搜索能力，但是局部搜索能力较弱。

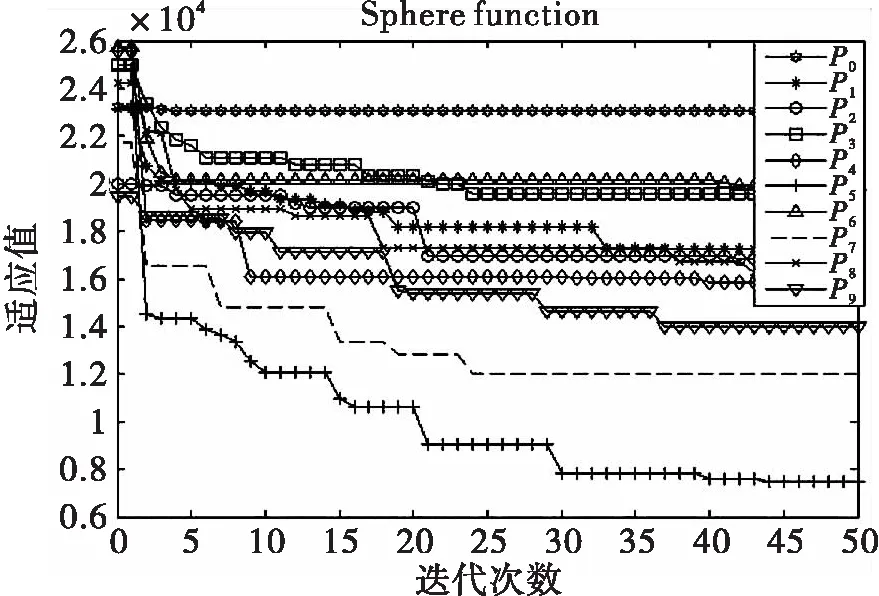
注：点所对应的迭代次数为横坐标刻度的10倍图5 星形有向结构中P0不固定时微粒适应值的变化Fig.5 Fitness evolution in the star-like directed structurewhen P0 is not fixed

(b)将中心点微粒P0固定在全局最优点(0，0，…，0)时，其余微粒的适应值的变化情况。由图6可以看出，中心点微粒P0固定在最优点时微粒向最优值靠近的速度明显快于不固定时的结构，在该结构下其余九个微粒迅速地向微粒P0运动，并都聚集在微粒P0的位置上，算法具有较快的信息传播能力，因此该结构下EPSO算法具有较强的局部搜索能力。

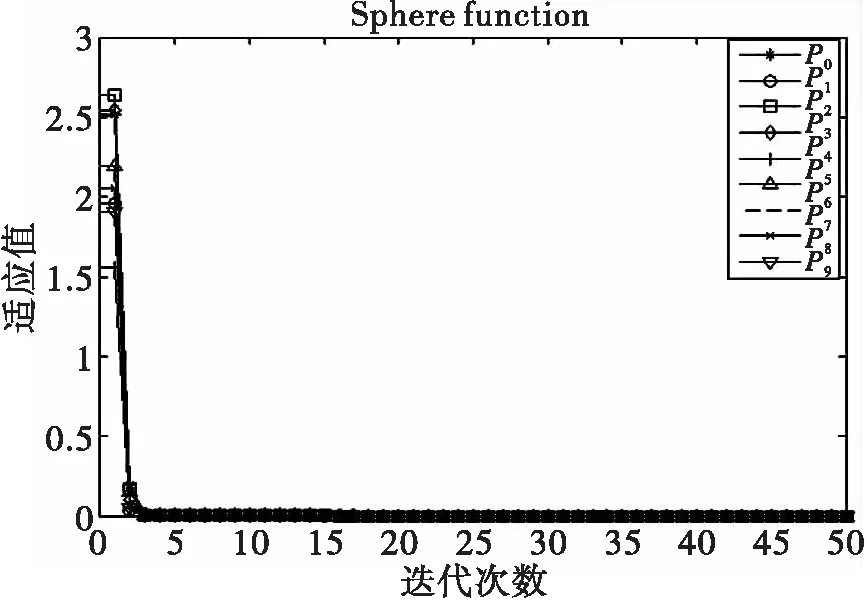
注：点所对应的迭代次数为横坐标刻度的10倍图6 星形有向结构中P0固定在最优点时微粒适应值变化Fig.6 Fitness evolution in the star-like directed structurewhen P0 is fixed in the optimal position

(c)当适应值最差的微粒在星形有向结构P0位置时，由图7可看出，该结构下微粒的适应值变化情况与函数最优值不固定在中心点时情况相近，因此该结构具有较强的全局搜索能力，同时局部搜索能力较弱。

3 不同有向结构作用下的EPSO性能分析

针对不同的有向拓扑结构，即环形有向结构、星形有向结构，研究EPSO的算法性能。实验环境：种群规模与函数维数相等，即N=n=30，w从0.9到0.4线性递减，最大进化代数为20 000.对于环形有向结构，根据2.1结论出度设为2，且全局最优点在(1，1…，1)点的函数设置c=1.5，而全局最优点在(0，0…，0)点的函数c=500.星形有向结构中设置c=1.5.表2记录了算法独立运行30次的平均值和方差。

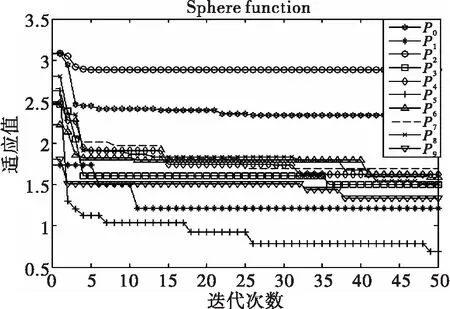
注：点所对应的迭代次数为横坐标刻度的10倍图7 星形有向结构中P0固定在最差点时微粒适应值变化Fig.7 Fitness evolution in the star-like directed structurewhen P0 is fixed in the worst position

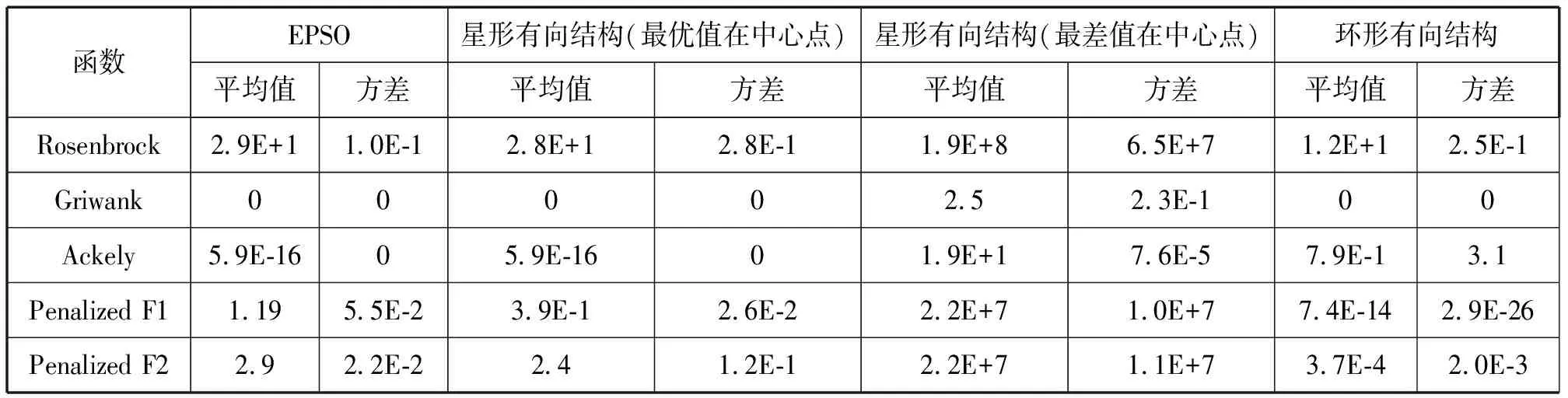
表2 EPSO作用在不同有向结构下的性能比较Tab.2 Performance comparison of EPSO with different directed structures

由表2可知，对于大多数函数而言，作用在有向环形结构上的EPSO算法性能较好。其原因可能是：有向环形结构较之其他结构具有较好的连通性，因此各节点的信息在环形结构中传播的较快；对EPSO而言，有向环形结构具有较少的邻居数量，因此在较小的加速系数c值下，算法具有较强的局部寻优能力。

4 总结

EPSO是一个新提出的算法。在EPSO算法中微粒之间的作用机制完全不同于在PSO算法下微粒之间的作用机制。EPSO算法具有较好的全局搜索能力，但是其局部寻优能力却非常弱。因此将EPSO算法作用于有向的种群结构，通过有向种群结构来提高算法的局部寻优能力。本文研究了有向环形结构、有向环基础上不同出度的有向结构以及中心点适应值不同(随机适应值、适应值最优、适应值最差)的星形有向结构的拓扑特征对EPSO算法性能的影响，得出了以下结论：(1)在有向种群结构中，节点的出度是影响EPSO算法性能的重要因素。节点的出度较小时的EPSO算法局部寻优能力优于出度较大时的EPSO算法。因为当节点的出度较小时，每个微粒受相邻较少微粒的作用，在较小的c值下，微粒在每一维上所受的合力较小，EPSO算法局部搜索能力较强。而随着节点出度值的增加，EPSO算法的全局寻优能力变强，而局部寻优能力变差。这是因为每个微粒所受相邻较多微粒的作用，具有较快的搜索速度，而不能精细的搜索某一区域。在出度值较大的情况下，c值较大时算法性能优于c值较小时的算法性能。因为当c值较大时微粒受到较大的合力作用，算法的全局搜索能力较强，而在较小的c值下，微粒仅能在其很小的邻域附近进行搜索，进而影响算法性能。(2)适应值的变化是影响EPSO算法的又一重要因素。当适应值较优的节点的入度增加时，与其连接的节点对应的微粒受到适应值较优微粒的力的作用，算法最优信息的传播速度较快。因此增加种群中适应值较好的微粒的入度值，能有效提高EPSO的算法性能。在特殊结构星形有向结构中，当最优适应值固定在中心位置时，其余微粒均受到最优适应值微粒的力的作用，以较快的速度聚集到最优位置附近，有效提高了EPSO算法的局部搜索能力。(3)有向环形结构较之其他有向结构具有较好的连通性，因此各节点的信息在环形结构中传播的较快；对EPSO而言，有向环形结构具有较少的邻居数量，因此在较小的加速系数c值下，算法具有较强的局部寻优能力。

参考文献：

[1] KENNEDY J，EBERHART R C.Particle Swarm Optimization[C]∥Proceedings of the IEEE International Conference on Neural Networks，Perth，Australia.Piscataway，NJ：IEEE Press，1995，IV：1942-1948.

[2] 莫思敏，曾建潮，谢丽萍.扩展的微粒群算法[J].控制理论与应用，2012，29(6)：811-812.

[3] 莫思敏，曾建潮.基于群体交互自组织种群结构的扩展微粒群算法研究[D].兰州：兰州理工大学，2012.

[4] 荆巧锋，程志谦.有向网络中节点分布的研究[J].洛阳工业高等专科学校学报，2007，17(5)：31-35.

[5] 黄红球.对有向网络理论及应用的一些研究[D].武汉：武汉理工大学，2007.

[6] 方峻，唐普英，任诚.一种基于加权有向拓扑的改进粒子群算法[J].计算机技术与发展，2006，16(8)：62-65.

[7] 尹礼寿，赵治荣.有向复杂网络中的度分布[J].运城学院学报，2009，27(2)：19-21.

[8] 马秀娟.基于BA 无标度的复杂有向网络演化模型[J].电子设计工程，2012，20(16)：11-13.

[9] 姚灿中，杨建梅.一种基于有向动态网络拓扑的粒子群优化算法[J].计算机工程与应用，2009，45(27)：15-17.

[10] MOHAIS A S，WARD C，POSTHOFF C.Randomized directed neighborhoods with edge migration in particle swarm optimization[C]∥Proceeding of the IEEE Congress on Evolutionary Computation，USA：IEEE Press，2004(1)：548-555.