步进电动机旋转角加速度测试与拟合建模

赵 浩， 冯 浩

（1.嘉兴学院，浙江嘉兴 314001； 2.杭州电子科技大学，浙江杭州 310018）

步进电动机旋转角加速度测试与拟合建模

赵 浩1， 冯 浩2

（1.嘉兴学院，浙江嘉兴 314001； 2.杭州电子科技大学，浙江杭州 310018）

介绍了步进电机的运动模型，采用自行研制的角加速度传感器对步进电机的单步运行、低频连续运行、低频丢步振荡、高频连续运行以及多种频率下的运行情况进行了实际的角加速度检测。采用不同的函数对角加速度曲线进行拟合，得到了相应的数学模型。找出了步进电机在正常连续运行时角加速度峰峰值与通电频率之间的关系式，为步进电机控制器或者控制算法的设计提供了技术支撑。

计量学；步进电机；角加速度；拟合建模

1 引 言

步进电机又称脉冲电机，是数字控制系统中的一种执行元件，其功用是将脉冲电信号变换为相应的角位移或线位移。近年来，数字技术和计算机技术的迅猛发展为其应用开辟了广阔前景。目前，步进电机已广泛应用于数控机床、绘图仪、轧钢机和自动仪表等多个方面［1～5］。但是步进电机在运行过程中存在明显振动，即角加速度，容易产生低频振荡和高频振荡，造成该现象的首因是步进电机的矩角特性近于正弦函数，且定子磁场以跳跃方式转动。

近年来一些学者对步进电机的角加速度波动及其抑制进行了研究。潘今宇在分析低速扫描中步进电机转速质量影响的基础上，介绍了用光电编码器测量转速稳定度的方法以及判定标准，并讨论了不同条件下步距角、惯性负载和微步距驱动对步进电机转速稳定度的影响［6］。张耀杰等分析了五相混合步进电机电磁转矩波动产生的原理，提出了利用时变周期信号的重复控制来抑制转矩波动的新思路，首先将时变的t域转矩信号变换为具有固定周期的θ域信号，再对其进行重复控制器设计，保持理想的驱动总电流，抑制转距波动［7］。郑晓冬等通过分析两相混合式步进电机的机械结构，理论推导了影响步进电机起动过程的多种因素，搭建了一套基于光电传感器的步进电机性能参数测量系统，并编写了数据收集和处理软件，最后从电机应用角度，提出了改进步进电机起动过程性能参数的方法［8］。王玉琳等提出了步进电机的几种速度调节方法，并通过对步进电机矩频特性曲线的分析，得出了步进电机的升频表格，提供了一个完整的软件升降频流程图［9］。

本文采用自制的旋转角加速度传感器［10］对步进电机实际运行时的多种情况进行了角加速度测试，相对于参考文献里的用光栅或者光电编码器这种测量平均角加速度的方法，更能够检测到步进电机瞬间的角加速度情况。采用多种函数对角加速度波动曲线进行了拟合，得到了相应的数学模型，并得到了步进电机角加速度波动峰值与绕组通电频率的关系式，为步进电机控制器或者控制算法的设计提供了相应的技术支撑。

2 步进电机运动模型

设步进电机每相每极控制绕组匝数为W，通入电流为I，转子在某一位置θ处转动了Δθ角，气隙中的磁场能量变化为ΔWm，则步进电机的静态转矩为：

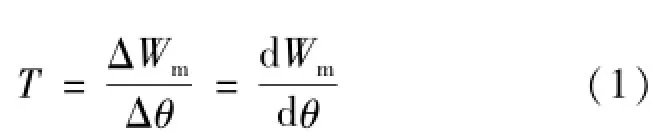
式中，Wm为步进电机气隙磁场的能量，当转子处于不同位置时，Wm具有不同值，即Wm是转子位置角的函数，且气隙磁场为：

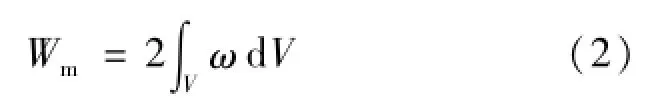
式中，ω＝HB／2，为单位体积的气隙磁能；V为一个极面下定、转子间气隙的体积。

当定、转子轴向长度为l，气隙长度为δ，气隙平均半径为r，与角度dθ相对应的体积增量为：

将式（3）代入式（2）得：

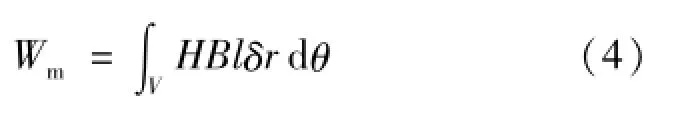
因为每极下的气隙磁势Fδ＝Hδ，再考虑到通过dθ所包围的气隙面积的磁通dΦ＝BdS＝Blrdθ，所以有：

由磁路的欧姆定律得：

式中，Λ为一个极面下的气隙磁导，则：

将式（7）代入式（1）得：

考虑到以下关系式：

式中，ZR为步进电机转子齿数，Zs为定子每极下的小齿数，G为气隙比磁导，即单位轴向长度、一个齿距下的气隙磁导，所以，步进电机的静态转矩为：

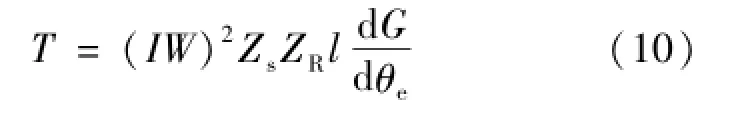
由于气隙比磁导G是转子位置θe的周期性函数，将气隙比磁导用傅氏级数来表示：

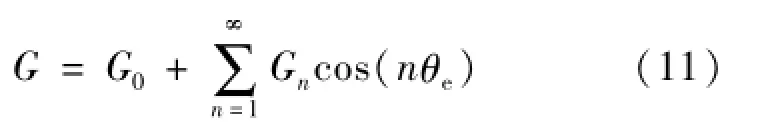
式中，G0为气隙比磁导的平均值，Gn为气隙比磁导中n次谐波的幅值，若略去高次谐波的影响，则式（11）可写成：

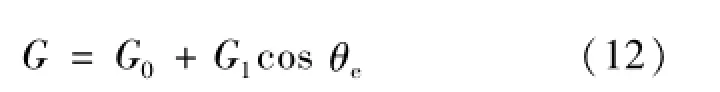
将式（12）代入（10）得

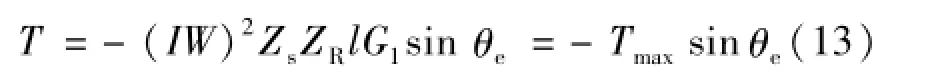
可见，步进电机单相通入电流时，产生的静态转矩T，在忽略高次谐波的影响时为失调角θe的正弦函数，其作用是总使转子位置趋向于失调角为零，与θe角增大的方向相反，在结构一定且磁路不饱和条件下静态转矩的大小与电流I的二次方成正比。

步进电机实际空载运行时受到空气摩擦阻力矩的作用，根据转矩平衡方程得：

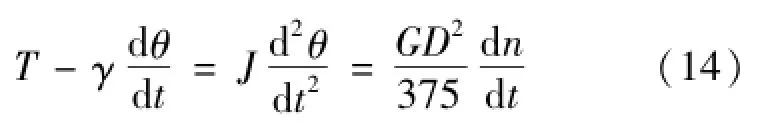
式中，γ为空气阻力矩系数，J为整个系统的转动惯量。

将式（9）和式（13）代入式（14）得：

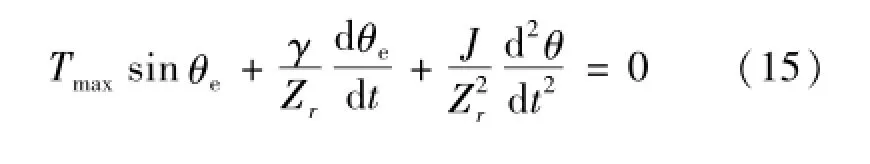
3 测试实验与拟合建模

实验平台由浙江大学方圆产业科技有限公司生产，型号为NMCL-II。步进电机型号是M10，各相绕组直流电阻为45Ω。采用配套驱动电源，型号为NMEL-10。

实验1：步进电机与自制角加速度传感器同轴相连，空载单步运行，三相单三拍运行时角加速度情况的测试结果如图1所示。

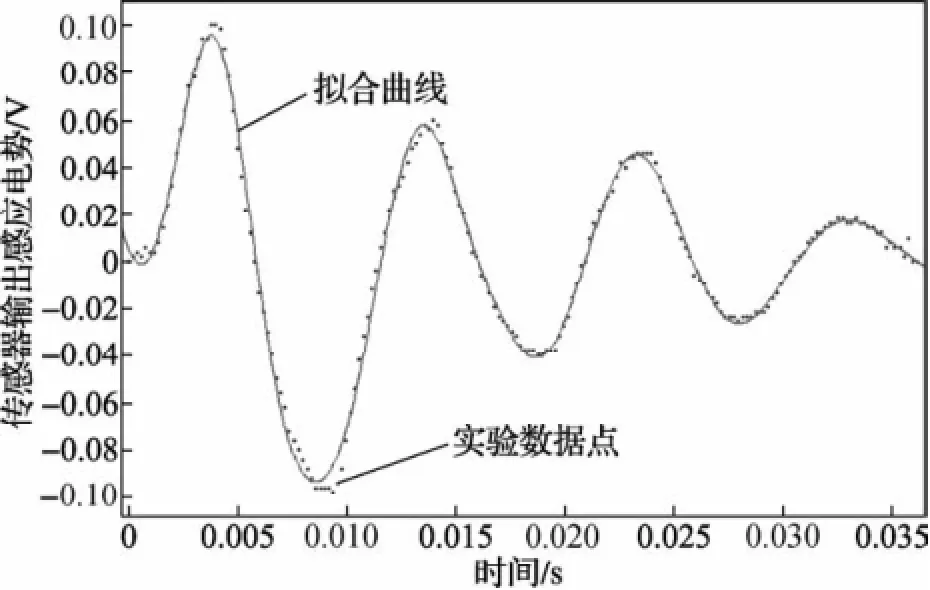
图1 三相单三拍单步的角加速度情况

对图1中角加速度曲线采用高斯函数进行拟合，得：

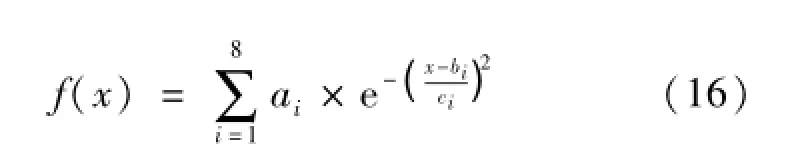
实验2：步进电机与自制角加速度传感器同轴相连，空载单步运行，三相六拍运行时角加速度情况的测试结果如图2所示。

对图2中角加速度曲线采用多项式函数进行拟合，得：

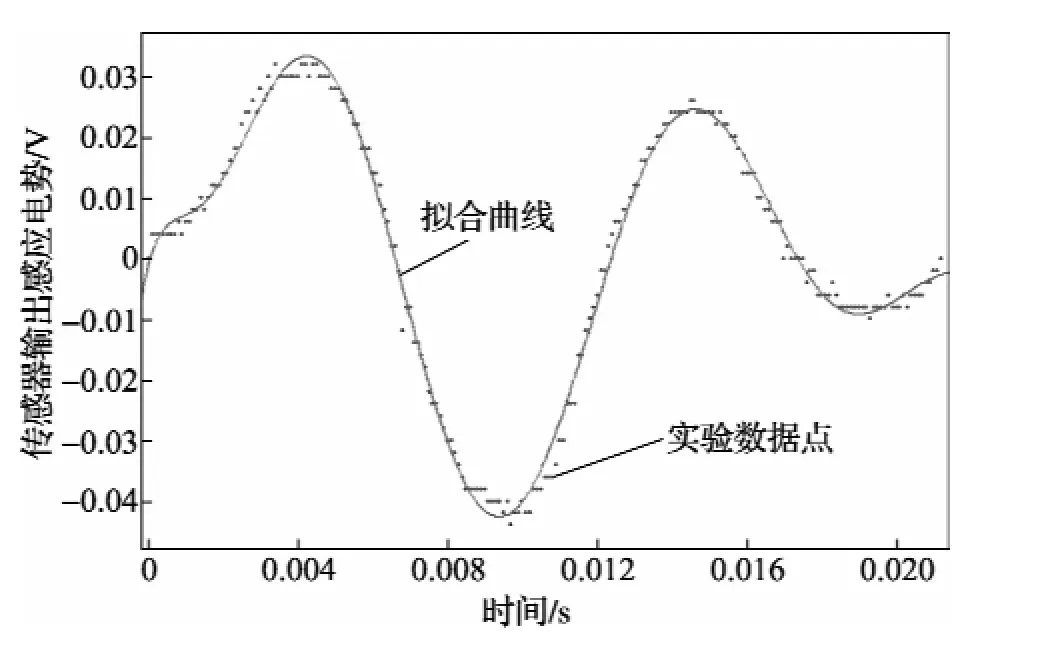
图2 三相六拍单步的角加速度情况

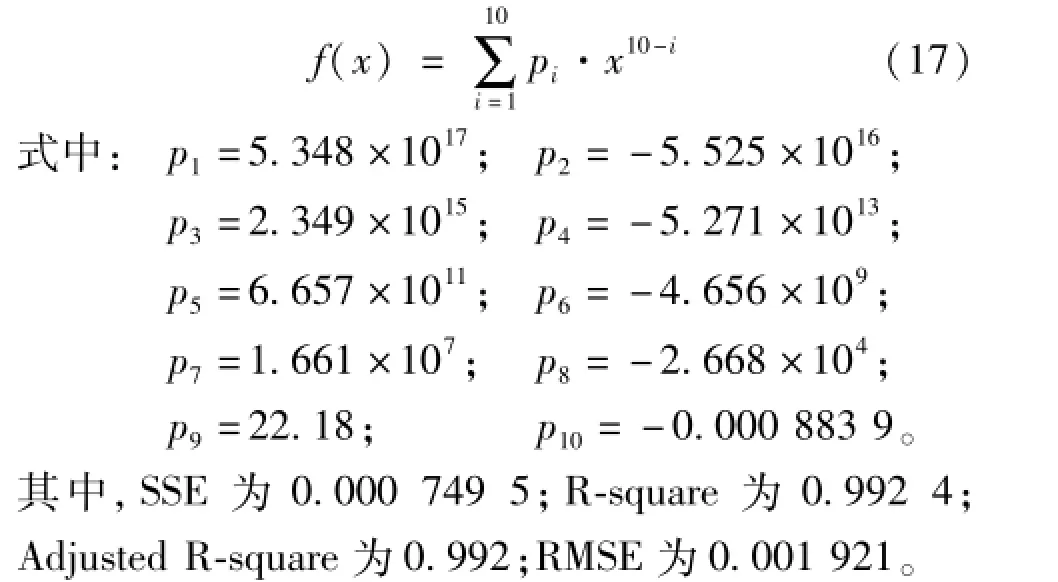
实验3：步进电机与自制角加速度传感器同轴相连，空载连续单三拍运行，提高步进电机的通电频率，当通电频率为10 Hz时，步进电机的角加速度情况如图3所示。

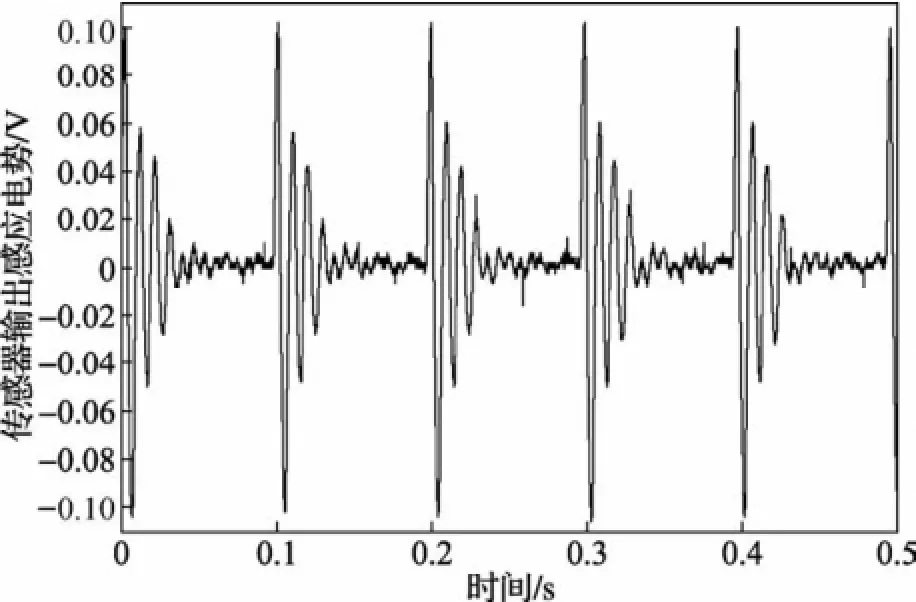
图3 步进电机低频连续运行时的角加速度情况

由图3可知，步进电机在低频连续运行时，转子每走一步的角加速度基本互不影响，即下一步总是在上一步基本达到稳态后才运行，其拟合曲线应为式（16）的延迟重复，延迟时间为通电频率的倒数，即0.1 s，由此可知其拟合数学表达式应为：

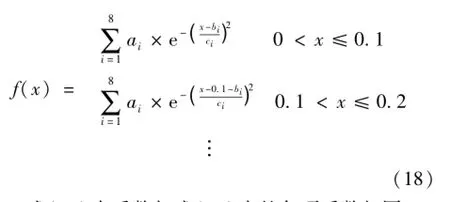
式（18）中系数与式（16）中的各项系数相同。

实验4：步进电机与自制角加速度传感器同轴相连，空载连续单三拍运行，当通电频率为64 Hz时，步进电机的角加速度情况如图4所示。

图4 步进电机64 Hz连续运行时的角加速度情况

由实验波形可知，此时的角加速度曲线仍为周期性函数，周期应为1／64秒，对其中某一段函数，如图5所示，采用多项式函数进行拟合得：

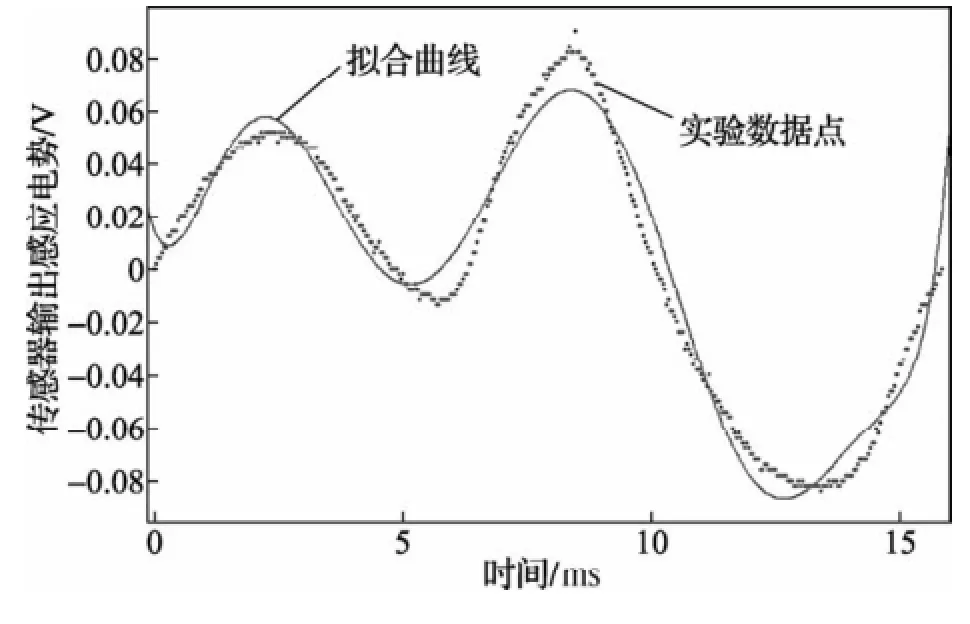
图5 步进电机64 Hz运行时某一周期的角加速度情况

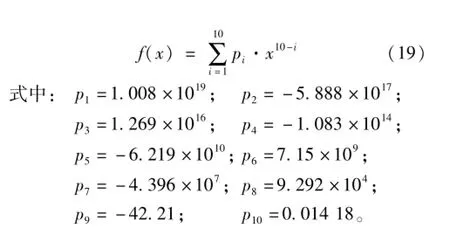
其中，SSE为0.028 7；R-square为0.970 2；Adjusted R-square为0.969 5；RMSE为0.008 611。

实验5：步进电机与自制角加速度传感器同轴相连，空载连续单三拍运行，提高步进电机的通电频率，当通电频率为98 Hz时，步进电机的角加速度情况如图6所示。

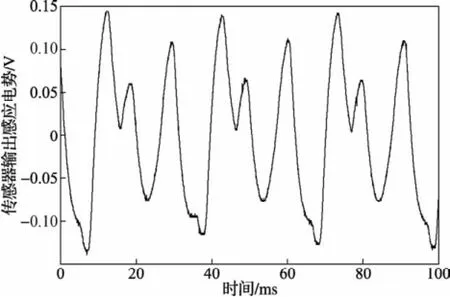
图6 步进电机98 Hz连续运行时的角加速度情况

由实验波形可知，此时的角加速度曲线为周期性函数，周期为1／98秒，对其中某一段函数，如图7

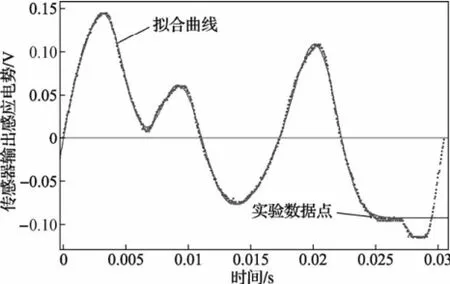
图7 步进电机98 Hz运行时某一周期的角加速度情况

所示，采用高斯函数进行拟合得：

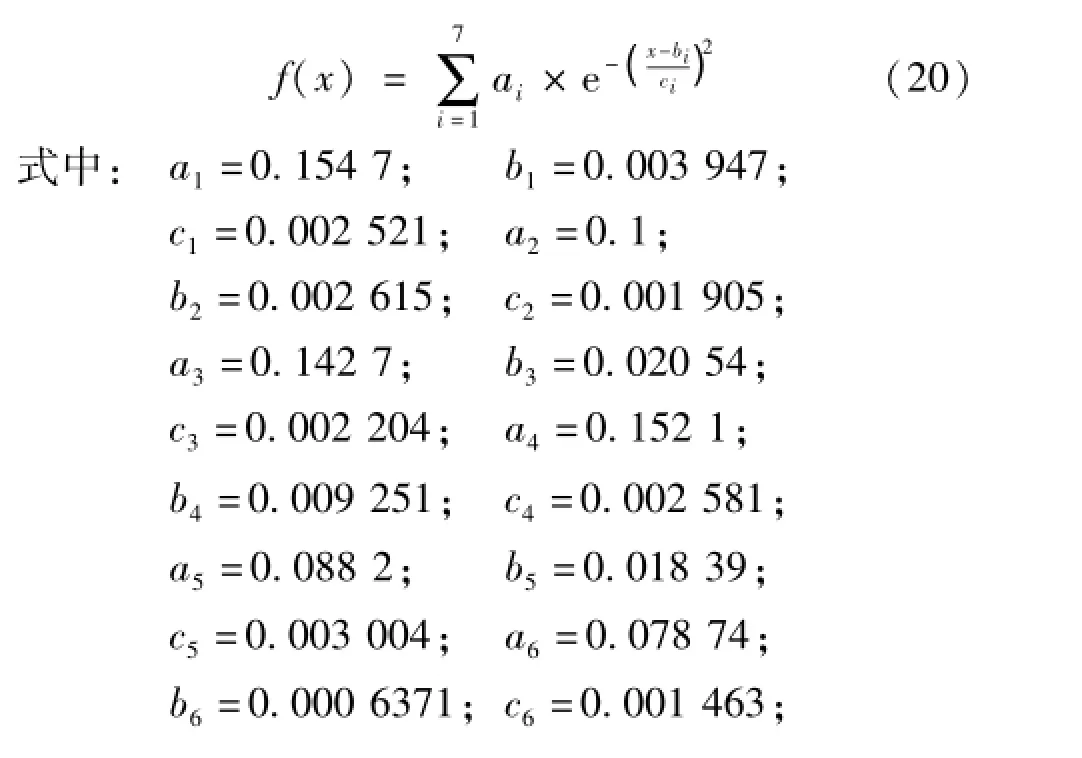
实验6：提高步进电机的通电频率为148 Hz，其他条件与实验5相同，步进电机产生丢步振荡，此时的角加速度情况如图8所示。

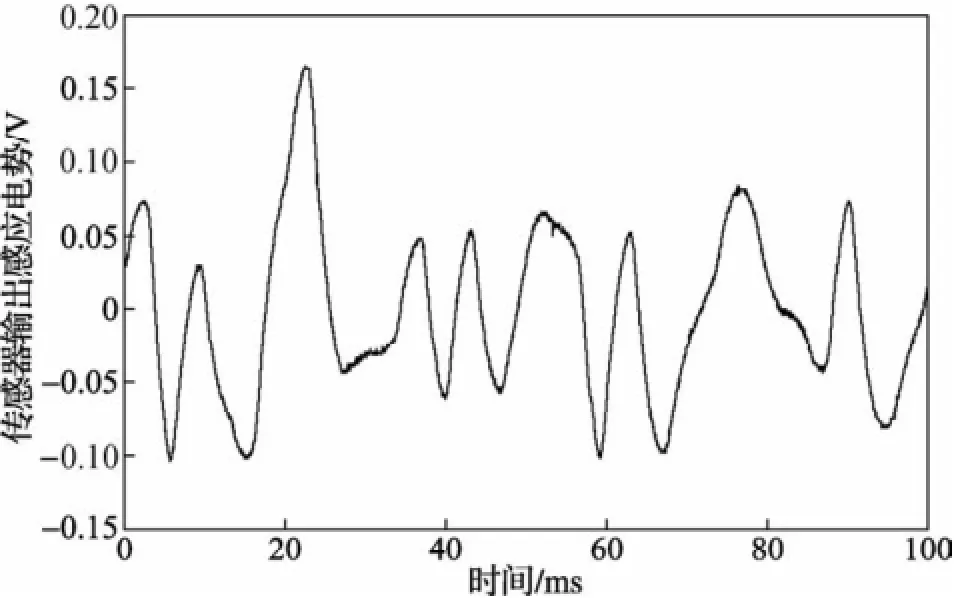
图8 步进电机丢步振荡时的角加速度情况

由图8可知，此时的角加速度曲线为非周期函数，实际的步进电机处于严重丢步振荡状态。

实验7：继续提高步进电机的通电频率，当通电频率超过200 Hz时步进电机处于正常连续运行状态，通电脉冲频率为300 Hz、375 Hz与460 Hz时角加速度情况实验结果分别如图9所示。

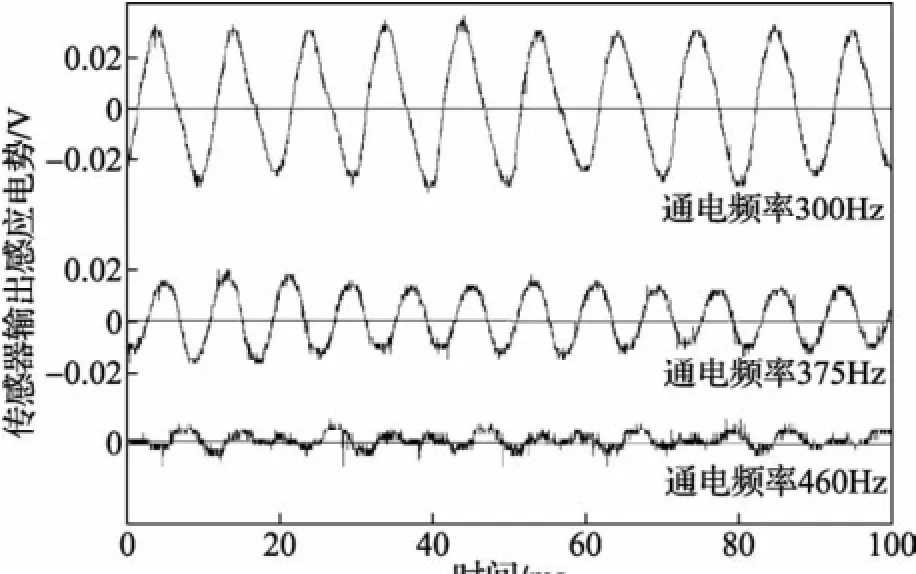
图9 步进电机连续运行时角加速度情况

由实验结果可知，此时角加速度曲线近似成周期性变化，且随着通电频率的不断提高，曲线的振幅逐渐减小。

对300 Hz的角加速度曲线某一周期段采用多项式函数进行拟合，得：

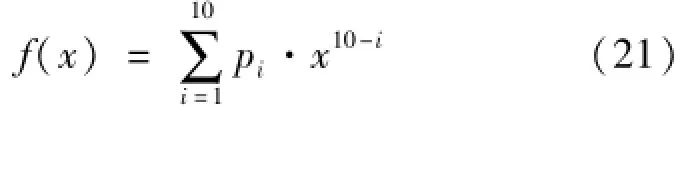
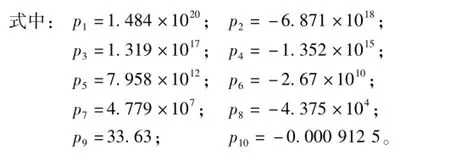
其中，SSE为0.000 375 4；R-square为0.996 2；Adjusted R-square为0.996 1；RMSE为0.001 238，拟合曲线如图10所示。

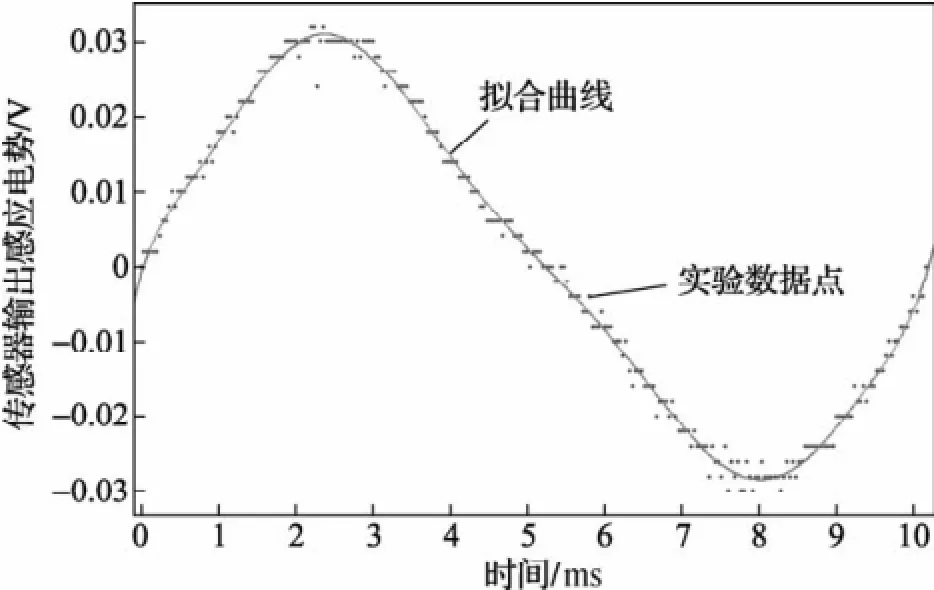
图10 步进电机300 Hz运行时某一周期的角加速度情况

为了找到步进电机正常运行时角加速度峰峰值与通电频率之间的关系，多次重复试验7，得到表1所示的实验数据。

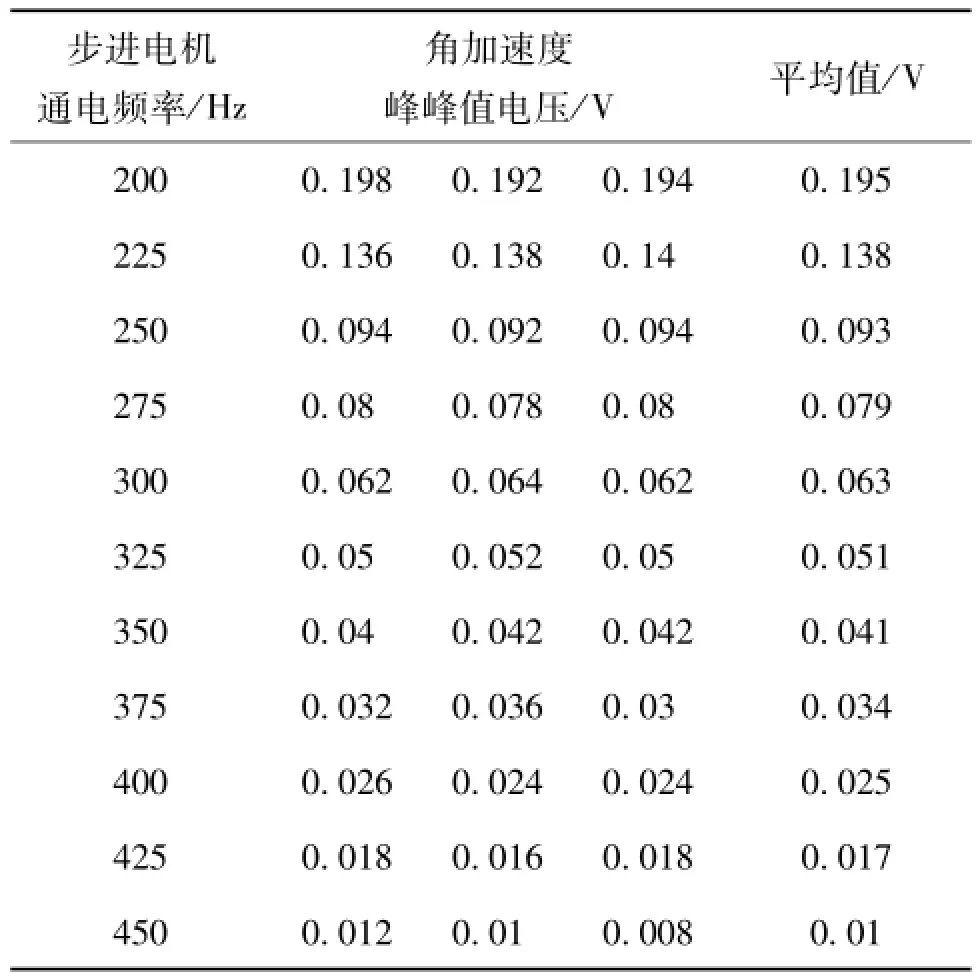
表1 实验数据

对表1的实验数据采用多项式函数进行拟合，得到的数学表达式为：

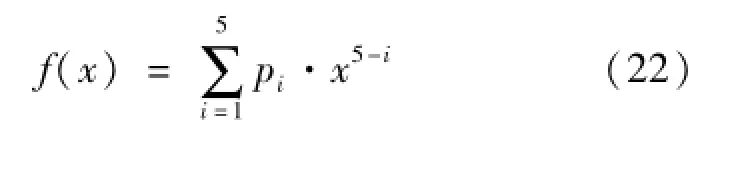
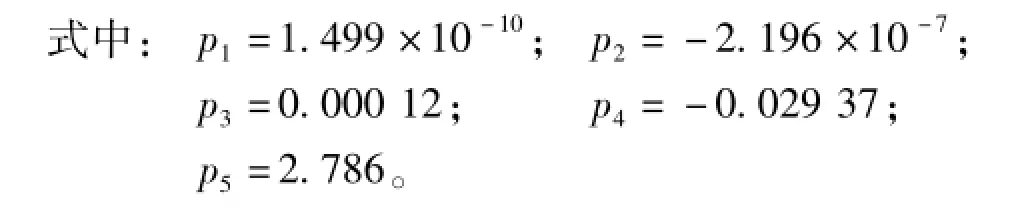
其中，SSE为0.000 054 2；R-square为0.998 3；Adjusted R-square为0.997 2；RMSE为0.000 300 5，拟合曲线如图11所示。

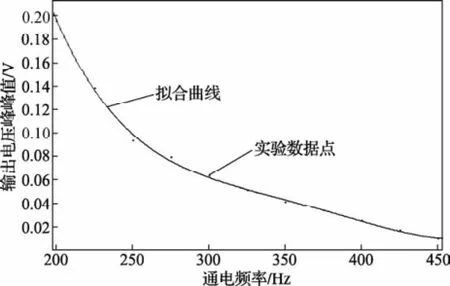
图11 步进电机角加速度峰峰值-频率曲线

4 结 论

本文采用自行研制的角加速度传感器对步进电机的单步运行、低频丢步、低频运行、高频运行等多种通电频率时的角加速度情况进行了测试，对实验结果曲线进行了拟合，得到了相应模型。为了减小步进电机实际运行时的角加速度，后续工作为研究和设计一种步进电机控制器，根据角加速度对其绕组输入电流进行相应控制，达到提高步进电机性能和扩大应用范围的目的。

［1］ 王宏涛，何晓波，陈琪.形状尺寸自动检测系统的设计［J］.计量学报，2011，32（3）：221－226.

［2］ 马维民，Hesselbach J，郇极.一种微型步进电机的微胶接装配方法的研究［J］.中国机械工程，2007，318（9）：1024－1027.

［3］ 武亚平.步进电机细分技术在DXD系列包装机中的应用［J］.食品与机械，2011，27（4）：109－111.

［4］ 沈文新，詹志杰，金岚，等.基于质量守恒原理的临界流喷嘴动态检定方法研究［J］.计量学报，2011，32（3）：213－216.

［5］ 项志宇，李斌.2D激光雷达的快速3D测距系统的设计与实现［J］.传感技术学报，2006，19（6）：2638－2642.

［6］ 潘今宇.步进电机转速稳定度的测定与分析［J］.上海航天，2005，22（5）：54－57.

［7］ 张耀杰，左贺，康龙云，等.抑制混合式步进电机转矩波动的时变重复控制［J］.中国电机工程学报，2004，24（11）：183－187.

［8］ 郑晓冬，邹鲲，孙以泽.两相混合式步进电机的响应及转速波动［J］.东华大学学报，2009，35（4）：463－466，487.

［9］ 王玉淋，王强.步进电机的速度调节方法［J］.电机与控制应用，2006.33（1）：53－56，64.

［10］ 赵浩，冯浩.一种电磁感应式角加速度传感器及误差分析［J］.计量学报，2012，33（6）：536－540.

Rotary Angular Acceleration Testing and Fitting Modeling of Stepping Motor

ZHAO Hao1， FENG Hao2
（1.Jiaxing University，Jiaxing，Zhejiang 314001，China；2.Hangzhou Dianzi University，Hangzhou，Zhejiang 310018，China）

Themotionmodel of the step motor is introduced，then the developed angular acceleration sensor is used for detecting the actual angular acceleration of the steppermotor on single-step operation，low-frequency continuous operation，low frequency lost step oscillation，high-frequency continuous operation and multiple frequencies operation，the angular acceleration curves are fitted by different functions，and the corresponding mathematical model are

.Finally，the relationship between the steppermotor angular acceleration peak value and frequency of the normal continuous operation are found，it can provides technical support for controller or control algorithm designation of the steppermotor.

Metrology；Steppermotor；Angular acceleration；Fittingmodeling

TB934

A

1000-1158（2014）05-0463-06

10．3969／j．issn．1000-1158．2014．05．12

2013-02-04；

2013-07-23

浙江省教育厅科研项目（Y201226082）；嘉兴市科技计划项目（2012AY1021）；2012年度嘉兴学院自制实验教学仪器设备研究项目（ZS201202）；2012年度嘉兴学院实验室开放项目；2013年度嘉兴学院南湖学院科研重点课题（N41472001－4）

赵浩（1983－），男，河北石家庄人，嘉兴学院讲师，主要研究方向为电机与新型传感器的设计。zhaohao204＠163.com

冯浩为本文通讯作者。zjhzfh＠126.com