实现质量量子基准的两种途径

李 辰， 韩 冰， 贺 青， 张钟华， 李正坤

（1.清华大学，北京 100084； 2.中国计量科学研究院，北京 100029）

实现质量量子基准的两种途径

李 辰1， 韩 冰2， 贺 青2， 张钟华2， 李正坤2

（1.清华大学，北京 100084； 2.中国计量科学研究院，北京 100029）

基于基本物理常数定义新的国际单位制成为21世纪国际计量界研究的热点，然而目前一些常数的测定尚未达到所需的不确定度范围。质量量子标准研究更是目前计量领域研究的重点和难点。经过30多年的发展，硅球法和功率天平法取得了重大进展，但目前发表的测量结果之间尚存在10－7量级的偏差。通过详细比较各国实现质量量子基准的两种途径，指出无论是依靠普朗克常数h还是阿佛伽德罗常数NA，在现阶段，取代国际千克原器尚有很长的一段路需要摸索。

计量学；质量量子基准；普朗克常数h；阿佛伽德罗常数NA；硅球；功率天平；能量天平

1 前 言

在国际单位制中，质量单位千克是目前唯一还依靠实物基准复现、保存量值的一个基本单位。它最初是以长度单位“米”来确定的，即1“立方分米”纯水在最大密度时的质量为“1千克”。1799年，法国根据这个定义制造了一个铂圆柱体砝码，保存在巴黎的国家档案局并被称为“档案千克”。其后的测量显示，档案千克并不准确地等于1立方分米最大密度纯水的质量，而是等于1.000 028立方分米最大密度纯水的质量。为了统一量值，国际米制委员会于1878年定制了3个铂铱合金圆柱体砝码，分别与“档案千克”比对，其中质量最接近的1个，在1889年第一届国际计量大会上被认定为“国际千克原器”（IPK）［1］。

从理论上说，国际千克原器的形状应当是一个球体。因为同等体积下球体的表面积最小，受外界的影响也最小。但考虑到当时的工业加工条件，球体的加工、调整和使用不便，国际千克原器的形状最终采用高度和直径均为39 mm的圆柱体。选用的材料为90%铂和10%铱的合金，该合金不易磨损，不易氧化，膨胀率和磁化率低。在150年前，这确实是当时制造砝码能够选择批量使用的最好材质。随后，国际计量局根据国际千克原器的材质、形状和要求，先后加工复制了一些副原器（彼此质量的相对偏差在10－9量级）发售给米制公约的各成员国，作为这些国家的原器或质量基准。我国从国际计量局引进No.60和No.64这2颗千克原器，其中No.60号作为国家千克质量基准，No.64号为国家千克原器的作证基准，最近的一次国际比对显示，我国的千克基准砝码质量值为1.0 kg＋0.295 mg，总不确定度为2.3×10－9（k＝1）［2］。

千克原器采用的材料为铂铱合金，经研究发现，这种合金尽管不易氧化，但它的质量日积月累仍然会发生细微的变化，年变化率约为10－10量级。考虑到众多千克原器的加工材料、工艺、年代均相差无几，因此严格意义上说，保存在国际计量局的国际千克原器也应该有了10－8量级的变化。

1999年第21届国际计量大会（CGPM）通过的决议7中已经明确提到：希望各国计量院努力攻克经典计量中这一最后的顽固堡垒，实现质量基准与基本物理常数或者原子常数的联系，为将来的千克重新定义奠定基础。在质量量子基准的重新定义中，现阶段有两种主流的技术方案，对应着两种不同的基本物理常数［3］。

2 普朗克常数h测定和电学天平方案

计量学家研究发现，如果可以将质量单位的复现关联到电学单位的复现上，原则上就可以实现质量单位的量子标准。目前，电学量均可溯源到约瑟夫森量子电压标准和量子化霍尔电阻标准，而这两种量子标准的量值是以基本电子电荷e和普朗克常数h这2个基本物理常数表示的。进一步的研究表明，在用电学天平的方法建立量子质量基准的过程中，电子电荷e被消去，只需普朗克常数h就可导出量子质量基准的量值。这样，量子质量基准就可借助量子电学基准而建立起来。一旦普朗克常数h测定值的不确定度小于2×10－8，就有可能通过普朗克常数h重新定义质量单位，实现质量量子基准。届时，质量单位千克可以定义为：“千克，是质量的单位，它的量值等同于普朗克常数h准确等于6.626 069X×10－34焦耳·秒，The kilogram，the unit ofmass，is such that the Planck constant is equal to exactly 6.626069X×10－34Joule second.”其中，X由各国测量结果决定。

在普朗克常数h测定方面，开展的比较成熟的方案是“功率天平”方案，它最早是由英国国家物理实验室（NPL）的Kibble B P博士提出的［4］，基本思路是把置于磁场中的载流线圈通以电流挂在天平上，载流线圈上受到的洛伦兹力与天平平衡时砝码上的重力相等，这样就可由电磁量导出砝码质量的量值。重点是通过天平把电学功率与机械功率联系起来，通过一系列的变换导出质量基准。式（1）为功率天平方案测量普朗克常数h的核心表达式，从量纲上可以体现出其功率平衡的含义

式中，m为砝码质量；g为重力加速度；v为功率天平运行中砝码速度；KJ-90为约瑟夫森常数；RJ-90为冯·克利青常数；U和I分别为载流线圈上的电压与电流大小。

国际上有多个研究机构从事功率天平方案的深入研究，包括美国的NIST、英国的NPL、瑞士METAS、法国LNE、国际计量局BIPM等。各国的功率天平的实验装置见图1，其具体设计各有侧重考虑。最新的测量数据：NIST［5］为h2007＝6.626 068 91（24）×10－34J·s，不确定度为3.6×10－8；NPL［6］为h2009＝6.626 071 23（133）×10－34J·s，不确定度为4.2×10－8；METAS［7］为h2011＝6.626 069 1（20）× 10－34J·s，不确定度为2.9×10－7。

2006年，中国计量科学研究院启动了质量量子基准项目，张钟华院士带领的团队一直致力于能量天平的研究。能量天平的工作原理与功率天平略有不同，它是通过天平把电学能量与机械能量联系起来。基本思路同样是借助于处于磁场中载流线圈，利用不同位置线圈磁场能量差值和重力场能量差值的平衡来测量普朗克常数h，测量核心公式为

式中，m为砝码质量；g为重力加速度；z为线圈的垂直坐标；KJ-90为约瑟夫森常数；RJ-90为冯·克利青常数；M为两组线圈之间的互感值；I1和I2分别为两组线圈的电流大小。

能量天平方案只涉及在z2和z12个不同的z坐标处准确测量的互感量M（z2）和M（z1），大大简化了测量过程。鉴于互感量M（z）为一个结构参量，不是场量，因此稳定性和重复性较好，可以用较长的时间采样，提高测量准确度。2013年能量天平课题组互感测量结果的分散性已经达到1.0×10－7，整套原理验证装置测量得到的普朗克常数为h＝6.626 104（59）×10－34J·s，测量不确定度为8.9× 10－6［8］。2014年课题组启动了第二套能量天平装置的设计和搭建工作，通过一些关键技术环节的改善，有望将不确定度缩小1个数量级。

3 阿佛伽德罗常数NA和硅球方案

尽管国际上用国际千克原器来定义宏观的质量单位千克，却又不得不以12C原子质量的1／12来定义微观的质量单位——原子质量单位，这样就出现两个质量单位如何协调一致的问题。而硅球方案正是将宏观质量与微观质量相联系的一种方案，它把质量定义在一定数量的原子上。一旦阿佛伽德罗常数NA精确测定后，质量单位千克就可以定义为：“千克，是质量的单位，它的量值准确等于5.018 451 6X×1025个处以基态的静止的自由12C原子的质量之和，The kilogram，unit ofmass，is the mass of exactly 5.018 451 6X×1025free carbon 12 atoms at restand in their ground state”，其中，X由各国测量结果决定。

图1 不同国家功率天平的实验装置图

硅球方案的基本原理为：制备一个高纯度的单晶硅球。测量硅原子摩尔质量MSi、包含着nSi个硅原子的晶胞体积VSi和单晶硅球的体积V，则单晶硅球的质量m可以通过代入下式得到

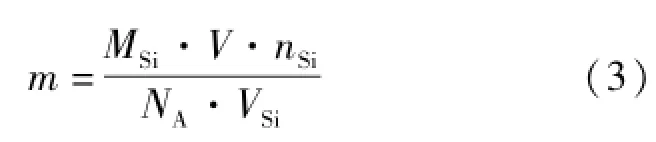
这里的关键是通过精密测量硅单晶的晶格间距、密度和摩尔质量，来提高阿佛伽德罗常数NA的准确度，从而降低单晶硅球质量m的不确定度。鉴于硅球方案从硅球的制备到最终参数的测量非一个机构可以完成，国际上专门成立了对应的工作组进行协调测量工作。2011年该工作组公布的最新测量结果为NA＝6.022 140 78（18）×1023mol－1，测量不确定度为3.0×10－8，成为目前在质量量子基准研究方面公布的最好测量结果［9］。

4 结 论

在目前的技术水平上寻求用某种自然规律或某个基本物理常数重新定义质量单位，技术难度确实较大。对比已发表的硅球法和功率天平法的的测量结果，各个结果的分散性比较大，还存在10－7量级的偏差［10］。但利用基本物理常数更新质量单位定义的方向是未来发展的趋势，值得肯定。根据国际计量局单位咨询委员会（Consultative Committee for Units，CCU）推荐，质量单位千克若采用普朗克常数h定义必须要达到以下3个条件：

（1）至少有3个独立的试验测量不确定度达到5×10－8；

（2）至少有1个实验的测量不确定度达到2 ×10－8；

（3）所有实验结果落在95%的置信区间内［11］。

从目前的测量结果来看，只有第（1）个条件达到，其他两个条件还需要不断努力，才能达到用基本物理常数定义质量量子基准的最终目的。

［1］ 韩冰，贺青，李世松，等.普朗克常数h测定与质量量子基准的最新研究进展［J］.计量学报，2013，34（1）：90－96.

［2］ Girard G.The third periodic verification of national prototypes of the kilogram（1988～1992）［J］.Metrologia，1994，31（1）：317－336.

［3］ 张钟华.量子计量基准的现状［J］.仪器仪表学报，2011，32（1）：2－5.

［4］ Kibble B P.A measurement of the gyromagnetic ratio of the proton by the strong field method.In：Sanders J H，Wapstra A H.Atomic Massesand FundamentalConstants 5［M］.New York：Springer，1976.

［5］ Steiner R L，W illiams E R，Liu R，etal.Uncertainty improvements of the NIST electronic kilogram［J］.IEEE TransactionsonInstrumentationandMeasurement，2007，56（2）：592-596.

［6］ Robinson I A，Kibble B P.An initial measurement of Planck's constant using the NPL Mark IIwatt balance［J］.Metrologia，2007，44（6）：427-440.

［7］ Eichenberger A L，Baumann H，Jeanneret B. Determination of the Planck constant with the METAS watt balance［J］.Metrologia，2011，48（3）：133-141.

［8］ 张钟华，李辰，贺青，等.能量天平研究进展［J］.计量学报，2014，35（4）：305－310.

［9］ Andreas B，Azuma Y，Bartl G，etal.Determination of the Avogadro constant by counting the atoms in a28Si crystal［J］.PhysRevLett，2011，106（3）：030801－4.

［10］ 张钟华，李世松.质量量子标准研究的新进展［J］.仪器仪表学报，2013，34（9）：1921－1926.

［11］ CCU.Report of the 18th Meeting to the International Committee for Weights and Measures［R］.BIPM，2007.

Two Approaches on Quantum Mass Standard

LIChen1， HAN Bing2， HE Qing2， ZHANG Zhong-hua2， LIZheng-kun2
（1.Tsinghua University，Beijing 100084，China；2.National Institute of Metrology，Beijing 100029，China）

Redefinition of the International System of Units（SI）on the basis of fundamental physical constants is hot issue for metrologists.However some constants determination does not meet the required uncertainty.The research of quantum mass standard is the emphasis and difficult points in themetrology especially.After 30 years developments，the silicon spheremethod and thewattbalancemethod have beenmade significantprogress.Nevertheless，the published results still have amagnitude of deviation about 10－7.Two popular approaches on quantum mass standard are made a detailed comparison，it is found thatwhether Planck constanthor Avogadro constantNA，there would be a long road to explore to eliminate the last artifact unit and it would be inappropriate time to substitute for international prototype kilogram at the present stage.

Metrology；Quantum mass standard；Planck constanth；Avogadro constantNA；Silicon sphere；Watt balance；Joule balance；

TB91

A

1000-1158（2014）05-0517-04

10．3969／j．issn．1000-1158．2014．05．22

2014-03-21；

2014-06-25

国家自然基金（51077120）；国家科技支撑计划（2011BAI02B03）

李辰（1983－），男，河北保定人，清华大学博士生，主要从事精密电磁测量研究。lichen0917＠qq.com