燃气表气阀配合面表面粗糙度稳健高斯算法

胡佳成， 崔 廷， 王婵媛， 沈小燕， 李东升

（中国计量学院计量测试工程学院，浙江杭州 310018）

燃气表气阀配合面表面粗糙度稳健高斯算法

胡佳成， 崔 廷， 王婵媛， 沈小燕， 李东升

（中国计量学院计量测试工程学院，浙江杭州 310018）

气阀配合面表面粗糙度决定着燃气表的机械与物理性能。为了加快表面粗糙度评定速度，根据高斯权函数的对称性，推导了高斯滤波器的快速卷积算法；采用光谱共焦传感器扫描工件表面轮廓的方式，比较了线性高斯滤波、回归高斯滤波、稳健高斯滤波在气阀配合面表面粗糙度提取过程中的优缺点。结果表明：新型稳健高斯滤波不仅能解决边界畸变问题，还能消除深谷或高峰等异常信号的影响，提高了表面粗糙度评定精度。

计量学；气阀配合面；表面粗糙度；回归高斯滤波；稳健高斯滤波

1 引 言

燃气表是一种应用广泛的测量燃气体积的专用流量仪表。阀盖与阀座是燃气表的核心部件，起着流量密封与机械运转功能，其制造工艺是影响燃气表计量精度的主要因素［1］。气阀配合面的表面形貌特征与其气密性、耐磨性、粘接性、抗疲劳性等有重要关联［2］。气阀配合面表面越粗糙，阀盖与阀座旋转配合时的间隙越大，气体越容易溢出，燃气表计量就越不准确［3］。因此，燃气表气阀配合面表面粗糙度信息的准确提取对提高燃气表计量准确性具有重要的指导意义。

2RC滤波器是早期表面粗糙度测量仪使用的滤波方式，它能较好地处理模拟信号，但由于2RC滤波器本身所固有的相位偏移特性，一定程度上会导致评定基准线的畸变［4］。为了解决传统滤波器存在的问题，出现了高斯滤波器、小波滤波器、样条滤波器、样条小波滤波器等相位补偿滤波器［5］。ISO 11562国际标准明确将零相移的高斯滤波中线作为表面粗糙度评定的基准线。

为解决传统高斯滤波器存在的边界畸变问题，出现了线性高斯滤波器；为在原始轮廓全部长度上进行表面粗糙度评定，出现了回归高斯滤波器；为消除深谷或高峰等异常信号的影响，出现了稳健高斯滤波器。本文针对这3种滤波器滤波结果的优缺点进行分析，并得出新型稳健高斯滤波在燃气表气阀配合面表面粗糙度评定过程中，不仅能解决边界畸变问题，还能消除表面深谷或刻痕的影响。

2 表面粗糙度快速高斯算法

气阀配合面表面形貌决定着工件的表面质量，与工件的机械与物理性能有重要关系。

定义f（x）为燃气表气阀配合面的表面测量轮廓，假设，

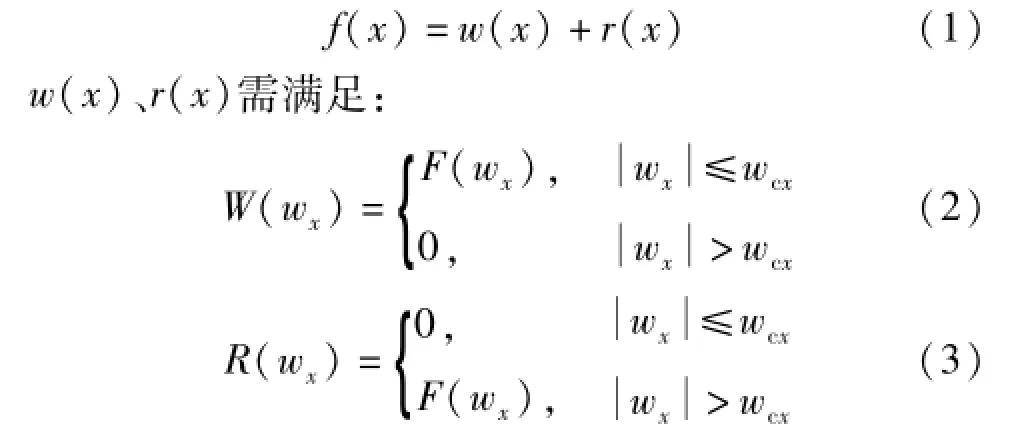
式中，W（wx）、R（wx）分别是w（x）、r（x）的Fourier变换，F（wx）是f（x）的Fourier变换，wcx是x方向的截止频率。

根据燃气表气阀表面轮廓的凹凸特征，选取适当的截止频率，可认为w（x）包含表面测量轮廓的形状误差与波纹度，即表面粗糙度评定的基准线，r（x）为表面粗糙度轮廓。

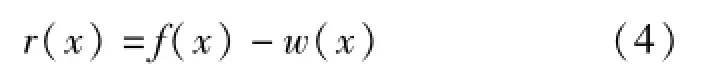
燃气表气阀配合面测量轮廓信号中的形状误差与波纹度属于低频信号，表面粗糙度属于高频成分。因此，表面粗糙度评定基准线可以将表面轮廓信号通过高斯低通滤波提取。

高斯滤波器具有线性相位特性，不存在传统2RC滤波器的相位偏移问题。高斯权函数的定义，

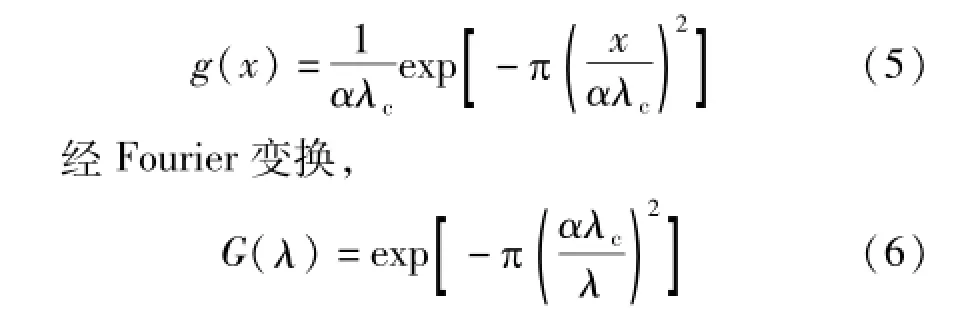
式中，x为离高斯权函数中心的距离；λ为采样轮廓信号波长；λc为滤波器截止波长。高斯权函数曲线如图1所示。

当λ＝λc时，高斯权函数通过率G（λ）＝0.5，因此得到，

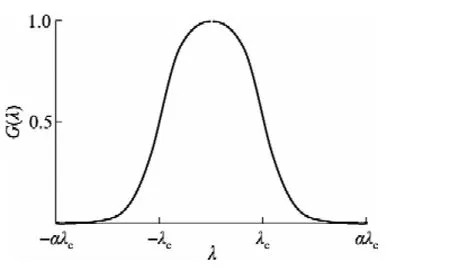
图1 高斯权函数曲线

表面粗糙度评定基准线w（x）是通过对表面测量轮廓f（x）与高斯权函数g（x）卷积运算得到，

一般来说，表面轮廓的采样数据是离散的，其长度也是有限的。在实际应用中，需对上面的公式进行离散化与有限化处理。

式中，f（i－k）是表面轮廓的离散表示，w（i）是高斯基准线的离散表示，g（k）是高斯权函数的离散表示，m是表面轮廓采样数据的点数，M是一个截止波长内离散高斯权函数的宽度，Δx是采样间隔。

根据高斯权函数的对称性，获取气阀配合面二维表面粗糙度评定基准线的快速卷积算法为，

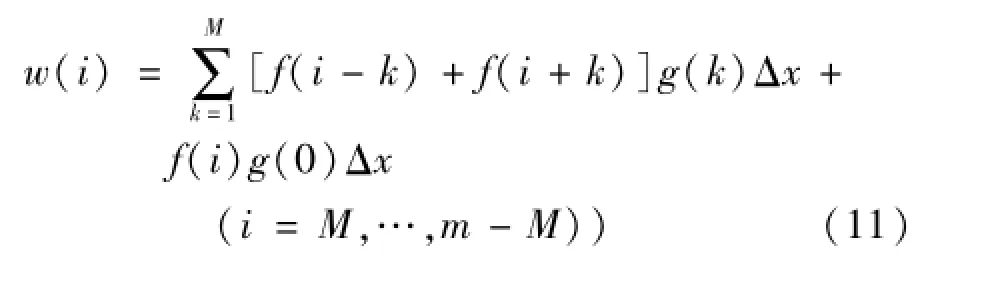
3 表面粗糙度稳健高斯滤波

采用光谱共焦法对燃气表气阀配合面进行表面粗糙度测量［6］。选用德国米铱公司生产的optoNCDT系列型号为IFS2401－0.12的光谱共焦传感器，线性量程为120μm，绝对误差为0.12μm，分辨力为5 nm，采样频率范围为100～2 000 Hz，24 V直流供电。任意选择一个气阀放置于定位精度为0.3μm的AEROTECH二维气浮平台上，搭建的测量装置如图2所示。为防止气阀在测量过程中摇摆晃动，检测速度不能过快，实验中设置二维气浮平台的速度为0.5 mm／s。

图2 光谱共焦法测量装置

3.1 线性高斯滤波

使用线性高斯滤波器对原始轮廓数据进行滤波时，需满足以下条件：原始轮廓不存在形状误差或已消除形状误差；原始轮廓已去除噪声；表面轮廓是等间距采样。但表面轮廓中存在高峰与深谷等异常点时，表面粗糙度评定会存在一定程度的失真。

设置气浮平台的运行长度为5.6 mm，使用光谱共焦传感器采集气阀配合面表面轮廓信息。首先对原始轮廓进行传统高斯滤波，设置滤波器的截止波长为0.8 mm，评定长度为5.6 mm，得到气阀配合面原始轮廓的传统高斯滤波结果如图3所示。

图3 气阀原始轮廓传统高斯滤波结果

由图3可以看出，气阀配合面二维原始轮廓的高斯滤波中线在两端出现畸变。分析原因可知，传统的高斯滤波器在原始轮廓不同位置所利用的加权平均的数目不同。在原始轮廓左右边界处，高斯滤波器权函数窗只有中间位置的一半，进行加权平均滤波时，只利用了原始轮廓一侧的数据。随着高斯滤波器权函数窗的移动，加权平均计算点的数量不断增多，高斯滤波中线不断上调，最终，二维原始轮廓的高斯滤波中线趋于正常。阀盖二维原始轮廓在进行传统高斯滤波时，边界处权重是中间位置权重的（0.5～1）倍，导致高斯滤波器在边界处与在中间位置滤波次数的不同，从而产生了边界畸变。

线性高斯滤波器为保证在边界处与在中间位置的滤波次数相同，需舍去原始轮廓左右边界处一定长度的数据采样点［7］。对阀盖配合面进行线性高斯滤波时，在左右各边界处截取一个截止波长的采样点，得到线性高斯滤波结果如图4所示。

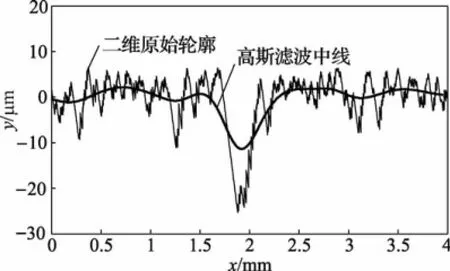
图4 气阀原始轮廓线性高斯滤波结果

由于在左右各边界处舍去了两个截止波长的数据，使得评定的原始轮廓数据由5.6 mm缩短至4 mm。当原始轮廓数据较长时，评价长度缩短无关紧要，而当原始轮廓长度有限时，就会出现滤波后评价信息不足的问题。

进行表面粗糙度参数评定时，将原始轮廓减去对应的高斯滤波中线，即可得到表面粗糙度轮廓。气阀配合面线性高斯滤波后的二维表面粗糙度轮廓如图5所示。

图5 气阀配合面二维表面粗糙度轮廓

对阀盖工作面的二维表面粗糙度进行评定，选取常用的轮廓算术平均偏差Ra进行计算，得到该不合格阀盖工作面的Ra值为2.848μm。

3.2 回归高斯滤波

定义修正后的回归高斯滤波权函数为：

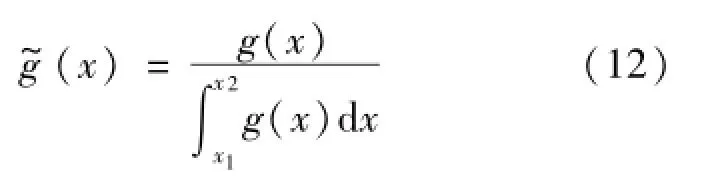
校正后的高斯权函数与加权平均的范围有关。当数据在中间位置时，回归高斯滤波权函数与线性高斯权函数功能相同；当数据靠近左右边界时，根据参与加权平均的数据点数不同，加大待处理点邻近数据的权重，同时减小较远点数据的权重，使得对原始轮廓不同数据点滤波时的总权重保持接近一致［8］。采用改进后的高斯密度函数提取评定基准线的方式如下，

由于气阀配合面的表面轮廓是离散采集的，将式（13）表示为离散形式。

对采样得到的同一条气阀配合面的原始轮廓进行回归高斯滤波，其结果如图6所示。

图6 气阀原始轮廓回归高斯滤波结果

从图6可以看出，使用回归高斯滤波器可以在原始轮廓的整个评定长度内进行滤波，完整地保留了原始轮廓信息，解决了线性高斯滤波器需要舍去边界点的问题。同样选取Ra进行计算，得到同一条阀盖工作面表面轮廓的Ra值为2.486μm，与采用线性高斯滤波器的Ra值相比略微变小。同时发现，无论采用线性高斯滤波器还是回归高斯滤波器，在原始轮廓的深谷处，滤波中线都会被下拉，导致获取的表面粗糙度信号有一定程度的失真。

3.3 稳健高斯滤波

线性高斯滤波与回归高斯滤波都不是一种稳健的算法。当原始轮廓中有高峰或深谷异常信号时，基准线会在高峰的地方被抬高，在深谷的地方被拉低，使得提取的表面粗糙度轮廓在这些地方出现畸变，从而不能准确地评定表面粗糙度相关参数。为了有效消除原始轮廓信号中高峰与深谷等异常信号的影响，出现了稳健高斯滤波器。

（1）Rk稳健高斯滤波器

国际标准ISO 13565中规定了一种Rk稳健高斯滤波器，用来消除原始轮廓中的异常信号［9］。采用ISO 11562中的线性高斯滤波器进行两步滤波，以提高滤波过程的抗高峰与抗深谷能力。其滤波过程如下：首先将原始轮廓通过线性高斯滤波得到高斯基准线；对所有低于高斯基准线的原始轮廓点，其值用高斯基准线上的对应值取代；将修改后的原始轮廓再次通过线性高斯滤波器，得到的新高斯基准线作为最终的表面粗糙度评定中线。气阀配合面的Rk稳健高斯滤波与回归高斯滤波对比结果见图7。

图7 气阀原始轮廓Rk稳健高斯滤波与回归高斯滤波对比结果

采用Rk稳健高斯滤波对气阀配合面进行表面粗糙度参数评定，得到轮廓Ra的值为2.692μm，比采用回归高斯滤波所得值偏大。采用Rk稳健高斯滤波器在一定程度上能消除原始轮廓中的高峰与深谷信号的影响，但不能消除很高峰和很深谷信号的干扰；这种滤波器采取两步迭代，滤波中线会整体上移，不能保证所有情况下的滤波结果都是稳健可靠的。

（2）新型稳健高斯滤波器

新型稳健高斯滤波器是将稳健估计原理引入到表面粗糙度评定中，根据原始轮廓信号的不同位置选择合适的估计模型，可有效消除异常信号对滤波过程的影响［10］。

在回归高斯滤波方法中引入幅度权函数δ（x），

新型稳健高斯滤波实际上包括高斯权函数与幅度权函数，高斯权函数用于频率区分，幅度权函数用于幅值抑制。当δ（x）＝1时，式（15）即为回归高斯滤波。通过不断迭代计算，寻求合适的δ（x），以消除深谷或高峰的影响。

对式（15）中的w（x）求微分并等于零，得到获取新型稳健高斯滤波中线的公式为，

式（16）的离散表示方式如下，

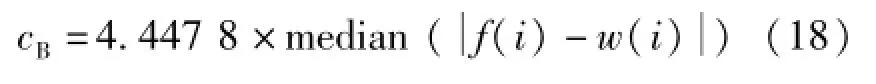
式中，median表示中值，也可以用均值表示。选择的稳健估计模型如下［11］，

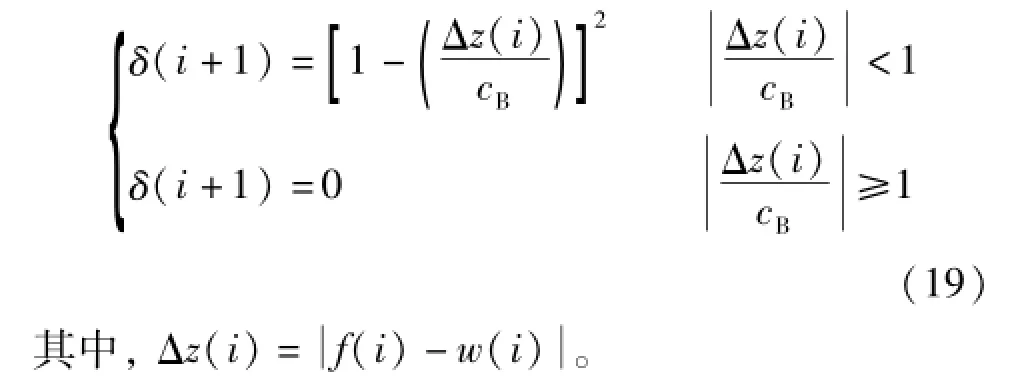
每次迭代求取w（i）时，利用线性回归滤波器，分别对f（i－k）δ（k）与δ（k）进行滤波。并引入残差函数如下，

对气阀配合面的表面轮廓进行稳健高斯滤波是一个不断迭代寻求最优解的过程。首先令δ（i）＝1，上述滤波即为回归高斯滤波，得到初始滤波中线w（i）；表面粗糙度轮廓是由原始轮廓减去高斯基准线得到的，对于存在很高峰与很深谷的地方，其值被认为异常点，在这些异常点处设置0≤δ（i＋1）＜1，以抑制其幅值；重新进行稳健高斯滤波，得到新的滤波中线w（i＋1）；循环往复，当前后两次的w（i）与w（i＋1）满足设定条件时，即可把w（i＋1）作为最后的高斯滤波中线。

对同一个气阀配合面的原始轮廓进行稳健高斯滤波，并与回归高斯滤波作对比，其结果如图8所示。由图8可以看出，对气阀配合面的原始轮廓进行了6次稳健高斯滤波，第5次与第6次的滤波中线已基本重合，则选择第5次稳健高斯滤波中线作为表面粗糙度的评定基准线，得到轮廓Ra值为2.969μm，比回归高斯滤波所得值2.486μm稍大，有效地保留了气阀配合面所存在的深谷或刻痕信息。

图8 气阀原始轮廓新型稳健高斯滤波

4 结 论

（1）燃气表气阀配合面表面粗糙度评定的快速卷积算法可有效加快滤波速度。

（2）对燃气表气阀配合面进行表面粗糙度评定时，线性高斯滤波器可解决边界畸变问题，回归高斯滤波器可在原始轮廓整个评定长度内滤波，新型稳健高斯滤波器可有效消除深谷或高峰等异常信号的影响。

（3）新型稳健高斯滤波器适合于燃气表气阀配合面的表面粗糙度参数评定，可有效保留气阀表面深谷或刻痕信息。

［1］ 刘立群.燃气表误差特性的分析［J］.计量与测试技术，2011，（1）：21－22.

［2］ 李伟，宋鹏云，曹登峰，等.低速运转气膜机械密封端面粗糙度对其密封性能的影响［J］.润滑与密封，2006，（10）：87－91.

［3］ 崔廷，沈小燕，胡佳成，等.激光三角法检测燃气表阀气密性研究［J］.光电工程，2013，40（7）：71－75.

［4］ 曾文涵，高咏生，谢铁邦，等.三维表面粗糙度高斯滤波快速算法［J］.计量学报，2003，24（1）：10－13.

［5］ Raja J，Muralikrishnan B，Fu S Y.Recent advances in separation of roughness，waviness and form［J］.Precision Engineering，2002，26（2）：222－233.

［6］ ISO 25178－2.Geometrical product specifications（GPS）—Surface texture：Areal—Part 2：Terms，definitions and surface texture parameters［S］.

［7］ Krystek M.A fastGauss filtering algorithm for roughness measurements［J］.PrecisionEngineering，1996，19（2－3）：198－200.

［8］ Brinkmann S，Bodschwinna H，Lemke H W.Accessing roughness in three-dimensional using Gaussian regression filtering［J］.Machinetools＆Manufacture，2001，41：2153－2160.

［9］ ISO 13565－1.Geometrical product specification（GPS）—Surface texture：profile method Profile method for surfaces having stratified functional properties—Part 1，Filtering and generalmeasurement conditions［S］.

［10］ 占伟伟，薛梓，刘胜春，等.直线度评价中稳健高斯滤波方法的研究［J］.计量学报，2010，31（6）：153－155.

［11］ ISO 11562.Geometrical product specifications（GPS）—Surface texture：Profilemethod－Metrological characteristics of phase correct filters［S］.

Robust Gaussian Algorithm of Surface Roughness for
Diaphragm Gas Valve Fitting Face

HU Jia-cheng， CUITing， WANG Chan-yuan， SHEN Xiao-yan， LIDong-sheng
（College of Metrology＆Measurement Engineering，China Jiliang University，Hangzhou，Zhejiang 310018，China）

Surface roughness of diaphragm gas valve fitting face determines itsmechanical and physical properties.In order to speed up the evaluation of surface roughness，the fast convolution algorithm of Gaussian filterwas derived based on the symmetry of Gauss function.With the means of spectral confocal sensor scanning surface profile of workpiece，the advantages and disadvantages of linear Gaussian filtering，regression Gaussian filtering and robust Gaussian filtering were compared.The results indicate that new robust Gaussian filter can not only solve the problem of boundary distortion，but also eliminate the effects of valley or peak abnormal signals.The evaluation accuracy of surface roughness has been improved.

Metrology；Gas valve fitting face；Surface roughness；Regression Gaussian filtering；Robust Gaussian filtering

TH92

A

1000-1158（2014）05-0420-05

10．3969／j．issn．1000-1158．2014．05．03

2013-12-08；

2014-04-22

国家自然科学基金（61205082）；浙江省自然科学基金（LQ14F050004）

胡佳成（1984－），男，浙江海宁人，中国计量学院讲师，中国科学院上海光学精密机械研究所博士，主要从事超精密测试技术研究。hujiacheng＠cjlu.edu.cn