复合评定法在三维粗糙表面评定中的应用

任志英， 高诚辉， 林建兴， 申 丁， 黄健萌

复合评定法在三维粗糙表面评定中的应用

任志英1，2， 高诚辉1，2， 林建兴1， 申 丁1， 黄健萌1，2

（1.福州大学机械工程及自动化学院，福建福州 350108；2.福州大学摩擦学研究所，福建福州 350002）

提出一种将双树复小波与分形理论相结合的复合评定方法。即利用双树复小波近似的平移不变性和方向性好等优点，将信号分解成更为细腻的低频和高频信号，同时根据多尺度下信号分形维数的不变性，利用图像灰度值自相关求得高低频信号的分形维数，通过计算高低频信号分形维数之间的差值（即分形维数距）来确定双树复小波的分解尺度。仿真结果表明复合评定法可以较好地提取基准面，且分形维数距确定分解层数的准确性通过均方根Sq值得到了验证；两个实例均说明，复合评定法可以很好地提取具有分形特征的纳米级三维粗糙表面基准或波纹度，为实际工程表面评定提供了可靠的理论基础。

计量学；粗糙表面；分形理论；双树复小波；复合评定

1 引 言

工程表面的粗糙度、波纹度以及表面不规则分布的沟槽、凹坑、凸台、划痕等多尺度形貌特征［1.2］等因素将直接影响工程表面的机械、物理特性。因此，准确地分离出表面的各种成分对于表面的功能评定将起到很大的作用。随着科学技术的发展，一般要求对表面在三维空间上进行分析［3，4］，小波变换因具有多尺度性质等，在三维表面粗糙度评定中得到了广泛的应用，但其存在平移变动性与方向性差等缺点［5］。基于小波和分形的表面粗糙度分析研究一直得到有关学者的重视［6］，目前用小波变换来提取表面形貌的分形维数已经取得了较好的效果［7，8］，但如何选取最优小波基以及小波分解尺度的确定依然是表面分析中的难点。

本文提出将双树复小波与分形理论相结合的复合评定法用于三维表面粗糙度的提取，即通过利用双树复小波克服传统小波分析中平移变动性与方向性差的问题，采用原子力显微镜等所得到的图像灰度值自相关函数来计算在各个尺度下基准面（或波纹度面）和粗糙度面的分形维数，并将各尺度下基准面（或波纹度面）的分形维数与粗糙度面的分形维数之差定义为分形维数距，通过计算比较分形维数距来确定双树复小波的分解尺度。最后将复合评定理论对具有分形特征的仿真粗糙表面和实际工程表面进行粗糙度评定，实验结果表明基于双树复小波与分形理论的复合评定法用于分形粗糙表面具有一定的可行性。

2 复合评定基础理论

2.1 双树复小波

双树复小波［9］（简称DT-CWT），它通过离散小波变换DWT实现，一个DWT产生实部，另一个DWT产生虚部，即上下两棵树。通过高度对称性的变换可实现两棵树的互相补偿。DT-CWT变换为克服odd／even滤波器的缺点，采用了Q-shift滤波器。该滤波器在两棵树的第二层及其以后的各层均为偶长度，具有近似理想的平移不变性。对于二维信号f（s）的复小波变换，可表示为二维尺度函数和6个高频方向小波函数的组合［10］：

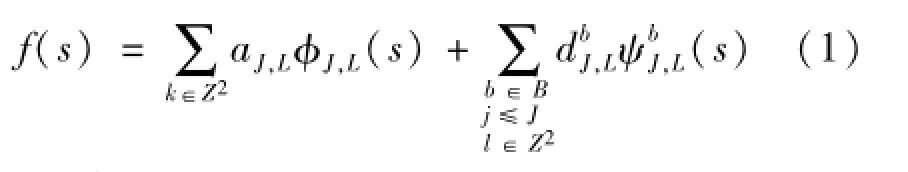
式中：s＝（x，y），x、y分别代表不同方向的二维信号；aJ，l和dj，l分别代表信号的光滑与细节部分；B＝｛±15°，±45°，±75°｝；J代表最粗糙的分解层；L代表细节的分解层；φJ，L为尺度函数；ψJ，L为小波函数。对于6个不同的高频子带的方向，各个子带的函数可表示为［10］：

由式（2）可知，DT-CWT变换具有6个方向的选择性，大大提高了对于表面形貌特征的提取与识别性能。

2.2 分形理论

研究表明许多工程表面及微纳表面具有某种与尺度无关的分形特性，说明这类表面形貌具有统计的自仿射性，即当表面适当放大后的表面形貌与原始表面形貌具有一定的相似性［11］。同时由于分形属性具有尺度不变性，很适合用来描述粗糙表面在各种尺度下的几何结构，分形属性被认为是粗糙表面的一种属性，表征尺度不变性的参数即为分形维数［12］。所以针对同一表面，其基准面（或波纹度面）的分形维数和去除基准面（或波纹度面）粗糙度面的分形维数应该最为接近。目前常见的表面分形维数计算方法有方盒计数法、幂率谱法、差分法、尺码法、结构函数法和小波法等［13，14］。分形维数的计算因选用的方法不同导致结果也各不相同，所以分形维数正确的确定方法对于表面粗糙度评定工作十分重要。本文研究对象为基于原子力显微镜下的微纳级表面，其表面各点像素的灰度值主要取决于实际测量的轮廓形貌，是试件表面形貌的真实反映，与表面的形貌、轮廓存在一一对应的关系。因此采用图像灰度值直接求取分形维数显得正确而有意义。根据这一特点，采用文献［15］中利用分形几何理论对表面图像的灰度值数据进行处理分析，从而得到了能够反映表面粗糙度特征的分形维数。

求分形维数的数学模型如下［16］：

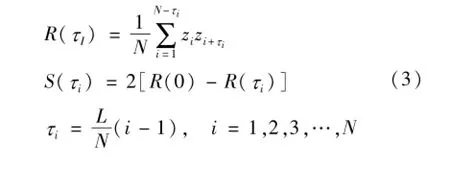
设图像灰度值数据构成的数据组为｛（x，y）；z｝，（x，y）代表像素点位置的坐标，z代表该位置上的灰度值，根据灰度值数据组，计算灰度值自相关函数，得到：式中：τi的物理意义是位置或距离；L是测量的长度或测量范围；N为取样总数，该值应由灰度值在被测表面上的密度来确定。对S（τi）和τi取自然对数后，拟合成一条直线，并计算出该直线的斜率值a和在纵坐标轴上的截距b，在双对数坐标下可得分形维数为：

2.3 复合评定表征分形表面粗糙度的数学建模

复合评定理论的基本步骤如下：

（1）通过DT-CWT分解三维粗糙度表面，得到各层的小波系数，并将小波系数转化为图像灰度值；

（2）采用自相关函数法，计算得到各层波纹度表面和粗糙度表面的分形维数；

（3）计算分形维数距，将得到最小分形维数距的分解层数确定为DT-CWT提取波纹度表面分解尺度；

（4）最后从原始表面形貌提取粗糙度表面以及基准面（或波纹度面）等信息，进行三维粗糙表面表征。

三维工程表面一般存在3种误差：粗糙度误差、表面波纹度误差和几何轮廓形位误差。在三维粗糙表面评定中，一般把具有低频特征信号的几何轮廓形位误差归结在中频特征信号的表面波纹度里。假设纳米三维表面微观形貌为Z（x，y），表面粗糙度为S（x，y），基准面（或波纹度面）和几何形状误差的总和为T（x，y），则三维形貌粗糙度的数学模型为：

将Z（x，y）进行式（1）DT-CWT变换，提取表面形貌的低频系数（f，φr），然后分别对各个层数的高频复小波系数置零处理，对其低频系数进行式（6）DT-CWT的反变换重构，即可求出分解中各层的基准面（或波纹度面）的信号T（x，y）：

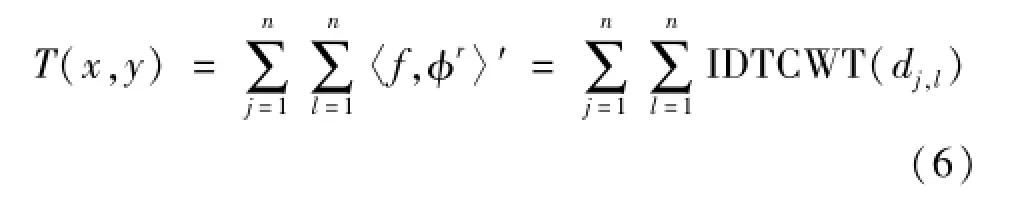
则表面粗糙度的数学模型为：

为获得各个尺度下基准面（或波纹度面）和粗糙度面的分形维数，将得到基准面（或波纹度面）的信号T（x，y）和粗糙度信号S（x，y）数据转换为图像灰度值数据。根据公式（3）和公式（4）求出在第J（J＝1，2，…，N）层可得到基准面（或波纹度面）分形维数DTJ和粗糙表面的分形维数为DSJ。

得出最小分形维数距w：

依据分形维数具有尺度不变性，在最小分形维数距的分解尺度下基准面（或波纹度面）与粗糙度表面的形貌特征最为相似，以此来确定DT-CWT可靠的分解层数，这样DT-CWT才能准确地提取纳米级三维功能表面粗糙度，为后续的三维参数准确评定奠定基础。

3 仿真验证

3.1 仿真分形粗糙表面粗糙度提取

为说明复合评定法能很好地应用在具有分形特征的三维粗糙表面中，通过Weierstrass-Mandelbrot（W-M）函数建立了一个采样点数为100 ×100，具有非平稳随机和分形特征的三维粗糙表面，见图1（a）。

图1 三维仿真表面及复合评定理论对其重构图

采用复合评定法对三维仿真粗糙表面进行评定，得到各层波纹度面和粗糙度面的分形维数和，如表1所示。从表1可知，当分解层数为3时，w达到最小，故确定DT-CWT分解层数为3层。最后分别对第3层的低频小波系数和高频系数进行重构，分别得到波纹度表面和粗糙度表面，见图1（b）和图1（c）。

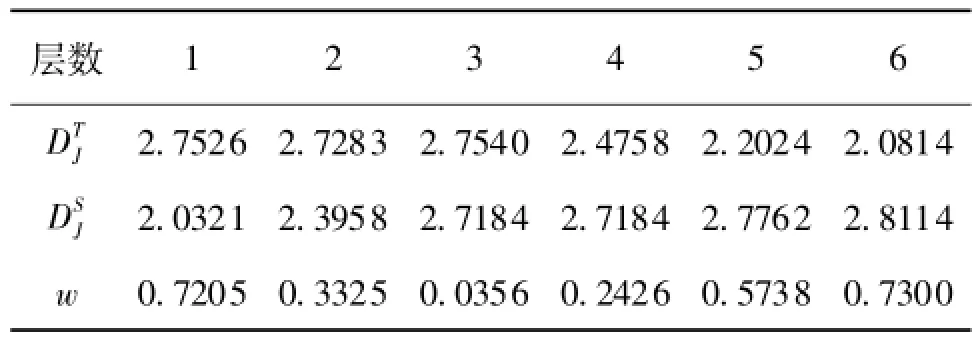
表1 三维仿真粗糙表面的波纹度面与粗糙度表面的D及w

3.2 仿真分形粗糙表面粗糙度提取正确性验证

判定复合评定法提取波纹度面的准确性，其实质是验证复合评定法在确定DT-CWT变换分解层数准确性。随着分解层数的改变所对应的三维表面表征参数均方差Sq值也会变化，表征参数均方根Sq的离散计算形式为：

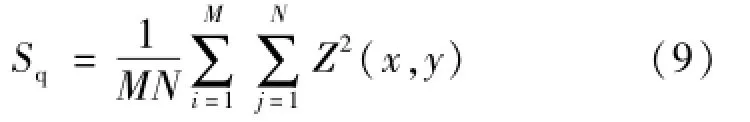
在三维粗糙表面评定中，一般把具有低频特征信号的几何轮廓形位误差归结在中频特征信号的表面波纹度中，则依次计算复合评定法在提取仿真分形粗糙表面波纹度后每层三维表面表征参数均方差

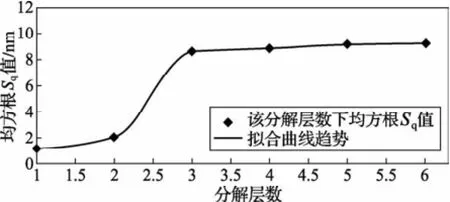
图2 分解层数与均方差Sq值变化趋势图

Sq值，得到的均方根Sq值变化趋势如图2所示。图中发现，随着复合评定分解层数的增加均方差Sq也逐渐增加，但当分解层数为3后，其表征参数均方差Sq趋于稳定值，因此说明通过分形维数距确定分解层数具有一定的准确性。

4 实例验证

4.1 实测镀膜光学元件表面粗糙度评定

实例1为具有分形特征的镀膜光学元件表面。图3为利用AFM扫描的三维镀膜光学元件表面，图4为导入MATLAB后实际三维镀膜光学元件表面。

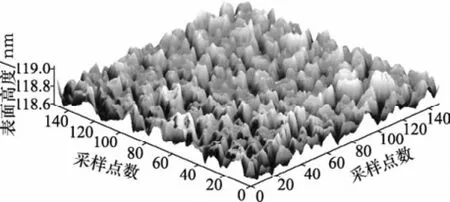
图3 基于AFM的镀膜光学元件表面样品图片三维图

图4 导入MATLAB后的三维镀膜光学元件表面

采用复合评定理论对图4中的光学元件表面进行提取，得到各层波纹度和粗糙度表面的分形维数DTJ和DSJ，见表2。

表2 镀膜光学元件表面的波纹度面与粗糙度表面的D及w

由表2可知，当分解次数为3时，w达到最小，确定DT-CWT的分解层数为3时，可得到光学镀膜表面的波纹度；当分解次数为7时，分离低频面的分形维数接近于2，说明该表面已无分形特征，确定DT-CWT的分解层数为7时，可得到光学镀膜表面的基准面。

最后分别对第7层低频小波系数和第3层的低频小波系数以及剩余的高频系数进行重构，分别得到基准面、波纹度表面和粗糙度面，如图5（a）、5（b）和5（c）所示。从图中可以看出，经镀膜后三维光学元件表面的波纹度面不够规整，局部个别地方较为凹陷与凸出，间接反映镀膜基底存在一定的缺陷；而其粗糙度面高度相互对称，反映了镀膜厚度较为均匀，说明该镀膜工艺较为良好。因此DT-CWT可以较好地分离镀膜光学元件表面各频段面形误差。

图5 复合评定对镀膜光学元件表面进行各频段分离结果图

4.2 多孔阳极氧化铝膜波纹度的提取

实例2为具有分形特征的多孔阳极氧化铝膜表面。多孔阳极氧化铝膜是一种典型的可用于制备多种功能纳米器件的自组织材料。图6是AFM获取的实际表面形貌图。

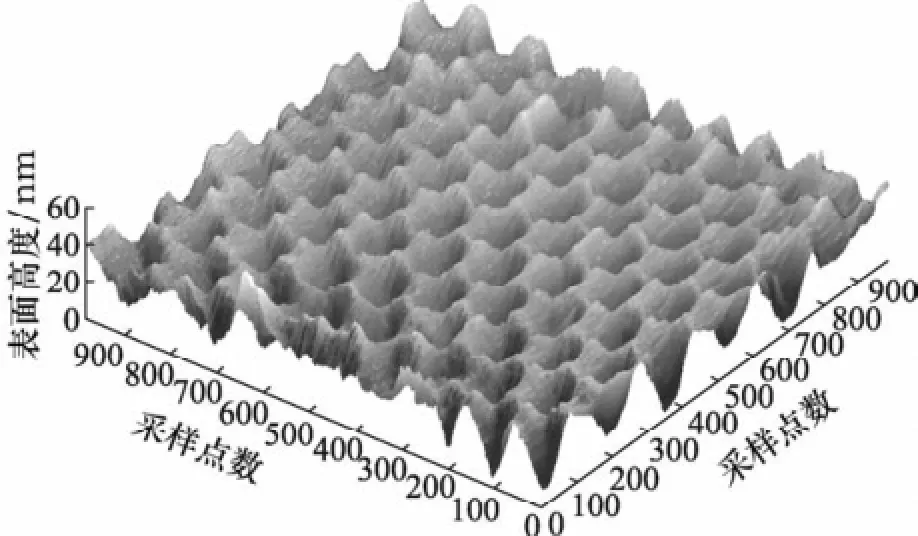
图6 多孔阳极氧化铝膜的AFM三维图像

将原子力显微镜获取的表面形貌的数据在Matlab平台上进行处理，为使得纳米三维基准面图像表达更清晰，提取200×200个采样点数，得到Matlab平台上的图像，见图7。采用复合评定法对图7多孔阳极氧化铝膜三维粗糙表面进行求解，得到各层波纹度表面和粗糙度表面的分形维数如表3所示。

图7 多孔阳极氧化铝膜的Matlab三维图像

表3 多孔阳极氧化铝膜波纹度与粗糙度表面的D及w

当分解层数为4时，w最小，确定该表面的分解层数为4层；当分解层数达到第7层后，波纹度表面的分形维数几乎不变，说明该提取表面已经达到毫无分形特征状态。最后分别得到波纹度表面和粗糙度表面，见图8（a）和图8（b）。将图8（a）和图7相比较发现，所经复合评定法提取的波纹度表面与原始粗糙表面的波纹走向具有一致性，且波纹度表面光顺自然，能更加清晰地分辨其特殊的多孔几何结构特点，为进一步评定此制备的合理性和优越性提供一个定量说明。

5 总 结

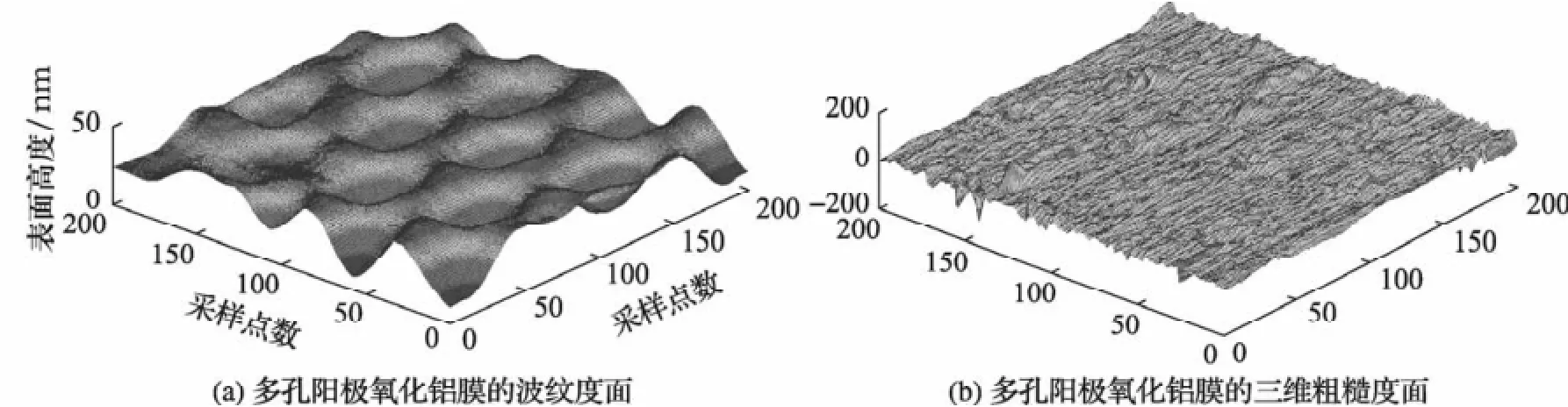
图8 多孔阳极氧化铝膜的波纹度面及粗糙表面

利用DT-CWT的近似平移不变性和多方向性以及分形理论中分形维数在多尺度变换中的不变性，提出了基于DT-CWT分形理论相结合的复合评定法，将其用于具有分形三维表面的基准或波纹度提取，实现了其不受取样长度的影响，经仿真和实验说明了复合评定法使用的可行性，得出如下结论：

（1）分形维数D具有不同尺度下的不变性，且能反映粗糙随机表面轮廓形貌的复杂程度，故D的确定十分重要。本文结合实际，根据仪器得到的灰度值采用自相关法来计算分形维数D显得合理；充分利用DT-CWT以及分形理论的优点，定义分形维数距w来确定DT-CWT的分解尺度，具有一定的理论可行性。

（2）采用复合评定法对仿真分形粗糙表面进行波纹度表面的提取，同时计算各分解层数下仿真分形粗糙表面均方根Sq值，验证说明利用w确定分解层数的准确性。

（3）复合评定法能很好地分离实际光学元件表面的低中高频面形误差，有利于后续客观地观察与分析其光学元件表面面形误差与性能之间的关系。

（4）采用复合评定法对实际多孔阳极氧化铝膜表面进行波纹度表面和粗糙表面的提取，提取的多孔阳极氧化铝膜表面波纹度能清晰分辨其独特的几何结构，有利于后期的孔参数测量，以及孔是否均匀分布等功能特性进行定量分析，可为实际工程分形表面特征提取提供一种新的方法。

［1］ Fisher J，Dowson D，Hamdzah H，etal.The effect of sliding velocity on the friction and wear of UHMWPE for use in total artificial joints［J］.Wear，1994，175：219－225.

［2］ Hall R M，Unsworth A，Siney P，etal.The surfacetopography of retrieved femoral heads［J］.Journalof MaterialsScience-MaterialsinMedicine，1996，7：739－744.

［3］ 杨大勇，刘莹，李小兵.小波分析及其在摩擦表面研究中的应用［J］.江西科学，2006，24（4）：238－241.

［4］ 孙延奎.小波分析及其应用［M］.北京：机械工业出版社，2005：31－58.

［5］ 陈武凡.小波分析及其图像处理中的应用［M］.北京：科学出版社，2002：27－30.

［6］ 李水根，吴纪桃.分形与小波［M］.北京：科学出版社，2002：1－7.

［7］ Grzesik W，Brol S.Wavelet and fractal approach to surface roughness characterization after finish turning of different workpiece materials［J］.Journalofmaterials processingtechnology，2009，209（6）：2522－2531.

［8］ Podsiadlo PW，Stachowiak G W.Fractal-wavelet based classification of tribological surfaces［J］.Wear，2003，254（11）：1189－1198.

［9］ Nick Kingsbury.The dual-tree comp lex wavelet transform：A new efficient tool for image restoration and enhancement［C］／／In Proceedings of European Signal Processing Conference，Rhodes，1998，319－322.

［10］ Jiang X Q，Blunt L.Third generation wavelet for the extraction ofmorphological features from micro and nano scalar surfaces［J］.Wear，2004，257（12）：1235－1240.

［11］ 陈辉，胡元中，王慧，等.粗糙表面分形特征的模拟及其表征［J］.机械工程学报，2006，42（9）：219－223.

［12］ 汪富泉，李后强.分形——大自然的艺术构造［M］.济南：山东教育出版社，1996：73－75.

［13］ 董连科.分形理论及其应用［M］.沈阳：辽宁科学技术出版社，1990：5－7.

［14］ Hasegawa M，Liu JC，Okuda K，etal.Calculation of the fractal dimensions ofmachined surface profiles［J］.Wear，1996，192（1－2）：40－45.

［15］ 李庆华，李振华.基于分形理论的表面粗糙度测量研究［J］.长春大学学报，2000，20（4）：47－48.

［16］ Wu JJ.Characterization of fractal surfaces［J］.Wear. 2000，239（1）：36－47.

Application of Composite Evaluation Method in the Assessment of Three-dimensional Rough Surface

REN Zhi-ying1，2， GAO Cheng-hui1，2， LIN Jian-xing1， SHEN Ding1， HUANG Jian-meng1
（1.College of Mechanical Engineering of Fuzhou University，Fuzhou，Fujian 350108；2.The Tribology Institute of Fuzhou University，Fuzhou，Fujian 350002）

Engineering surfaces always have fractal characteristics and now a composite evaluationmethod is proposed in which the dual tree complex wavelet combined with fractal theory.By using the dual-tree complex wavelets approximate translation invariance and good directions，signal is decomposed into a more delicate low and high frequency signals. Meanwhile，according to the invariance of the signals＇fractal dimension undermulti－scale，the fractal dimension of signals is obtained by the use of the autocorrelation image gray value，and the dual tree complex wavelets decomposition scale is verified by calculating the different fractal dimensions between the high and low frequency signals（the fractal dimension distance）.The simulation results show that the datum can bewell extracted by the use of the composite evaluationmethod，and the accuracy of decomposition level which is confirmed by the fractal dimension distance is verified by the use of the rootmean square value.Two examples illustrate that reference and waviness of the nano-scale three-dimensional rough surfaceswhich have fractal characteristic can be well extracted by the use of the composite evaluation method，which provides a reliable theoretical basis for the assessment of the actual engineering surface.

Metrology；Rough surface；Fractal theory；Dual-tree complex wavelet；Composite assessment

TB92

A

1000-1158（2014）05-0414-06

10．3969／j．issn．1000-1158．2014．05．02

2013-09-12；

2014-02-27

国家自然科学基金（51175085）；国家青年自然科学基金（51205062）；福建省教育厅A类资助项目（JA13059）；福州大学科技发展基金（600907）.

任志英（1980－），女，浙江嵊州人，福州大学讲师，博士研究生，主要从事摩擦学中表面表征方法研究。renzyrose＠126.com

高诚辉为通讯作者。gch＠fzu.edu.cn