矩形线圈和圆形线圈屏蔽环境磁场的效能比较研究

董全林， 刘雪萍， 范运强， 徐晓斌， 宋凝芳， 张春熹

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

矩形线圈和圆形线圈屏蔽环境磁场的效能比较研究

董全林， 刘雪萍， 范运强， 徐晓斌， 宋凝芳， 张春熹

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

研究了用3组轴线相互垂直的线圈组成的磁场屏蔽系统。通过毕奥-萨伐尔定律并借助Matlab软件，分析比较了矩形线圈和圆形线圈两种屏蔽系统的磁场分布情况。实验数据表明矩形线圈屏蔽系统的性能要略优于圆形线圈屏蔽系统。其结论可应用与原子陀螺、电子显微镜等器件的设计中。

计量学；地磁补偿；磁场屏蔽；矩形系统；圆形系统

1 引 言

在冷却和俘获原子实验中，除了反Helmholtz线圈提供的对称磁场，在切断线圈电流背景磁场关闭之后，原子团还受到地磁场等杂散磁场的影响［1］，使运动电荷发生偏转、原子能级发生分裂，给实验带来不容忽视的误差［2，3］，因此必须补偿环境磁场。

磁场屏蔽是电磁屏蔽的难点。由于磁场是矢量，许多实验中提出用3组轴线相互垂直的线圈共同作用，以不同方向产生的磁场与外磁场矢量叠加［4～5］。给线圈通以适当的电流，使叠加处的线圈激励磁场和环境磁场大小相等方向相反，从而补偿环境磁场，使预屏蔽区域达到零磁场效果。

在一定范围内，环境磁场可近似为均匀磁场，屏蔽系统的作用即产生尽量均匀的磁场，所以应在产生均匀磁场方面对屏蔽系统进行优化。同时采用不同线圈形状的屏蔽系统，通以相同电流在相同区域内产生磁场的磁感应强度不同，显然使用较小电流即可屏蔽掉环境磁场的屏蔽系统是较优选择。基于矩形线圈和圆形线圈制作工艺简单考虑，本文分析比较了矩形线圈和圆形线圈两种屏蔽系统的屏蔽情况。

2 理论分析

2.1 矩形线圈屏蔽系统

如图1（a）所示，用3组矩形线圈组成立方体对磁场屏蔽，以立方体中心为原点建立直角坐标系，立方体沿X轴、Y轴、Z轴的棱长分别为2a、2b、2c。每组线圈通以相同电流，分别与X轴、Y轴、Z轴正向成右手螺旋关系，进行3个方向的补偿。图1（b）为矩形线圈屏蔽系统结构图。

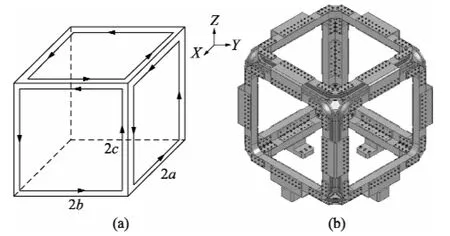
图1 矩形线圈屏蔽系统示意图和结构图

立方体内任意点的磁场强度是各个棱边在该点产生的磁场强度的叠加，根据电磁学知识，载流直导线在距离其R处的磁感应强度大小为：

式中，I为通电电流，R为考察点距导线距离，φ1、φ2分别为考察点到导线两端的连线与考察点到棱边距离连线的夹角。

图2 棱1在P点产生的磁场示意图

如图2所示，考察立方体底部矩形线圈与X正半轴相交垂直的棱1在立方体内任一点P处的磁感强度［6］。式中，li是与第i条棱电流同方向的单位矢量，eRi是第i条棱到P点的垂直距离矢量。利用式（3）可以模拟出所需磁场分布。

2.2 圆形线圈屏蔽系统

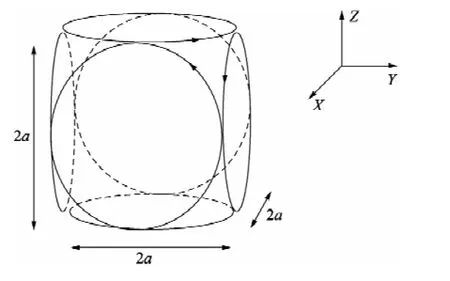
图3 圆形线圈屏蔽系统示意图

如图3所示，用3组圆形线圈对磁场屏蔽，与矩形线圈屏蔽系统类似，以立方体中心为原点建立直角坐标系，3组线圈的直径均为2a。每组线圈通相同的电流，分别与X轴、Y轴、Z轴正向成右手螺旋关系，进行3个方向的补偿。立方体内磁场是各个线圈激发磁场的叠加，下面以底部线圈为例推导单个线圈在立方体内任意一点P（x，y，z）的磁感应强度，如图4所示。图中r为原点到场点P的距离矢量。

根据毕奥-萨伐尔定律，单个线圈在任一点的磁感应强度为：

式中，I为通电电流，Id l为电流元，R为电流元到场点的距离矢量，R为R的标量大小。对于底部线圈，由几何关系，有以下等式：

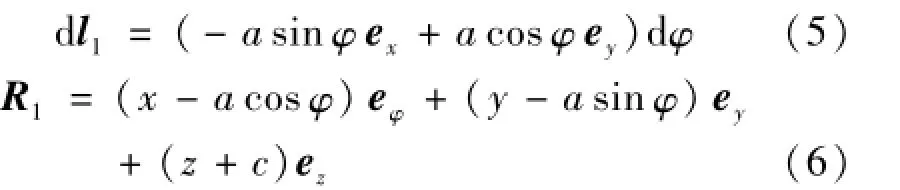
则底部线圈在P点产生的磁感应强度为：

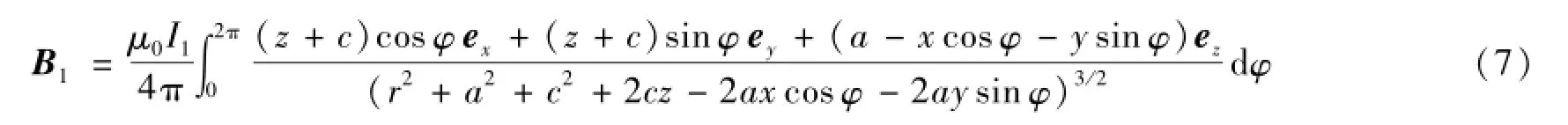
式中，r2＝x2＋y2＋z2，a为线圈半径，c为线圈到Z＝0平面的距离，φ为原点到电流元直线与X轴的夹角。

其他线圈在点产生磁场的磁感应强度可以用同样的方法求出，则P点的总磁感应强度为：

利用式（7）、式（8）可模拟所需磁场分布。

图4 底部线圈在P点产生磁场示意图

3 磁场模拟与结果分析

实验中，矩形线圈内边长为430 mm，外边长为485.8 mm（圆形线圈内径为430 mm，外径为485.8 mm），每个线圈均为575匝，每组线圈通电电流均为0.025 A。以系统中心为中心的边长为10 cm的正方体区域是预屏蔽区域。

1）首先分析中心轴线上和中心平面上的磁场分布。因为每个线圈采用相同参数，磁场分布具有对称性，所以只给出磁感应强度随X轴的变化和X＝0平面上的磁场分布。在屏蔽区域内矩形系统激发磁场的磁感应强度比圆形系统稍大，即若预屏蔽掉相同磁场，矩形系统所需电流较小。见图5～图8。

图5 矩形系统X轴上磁场分布

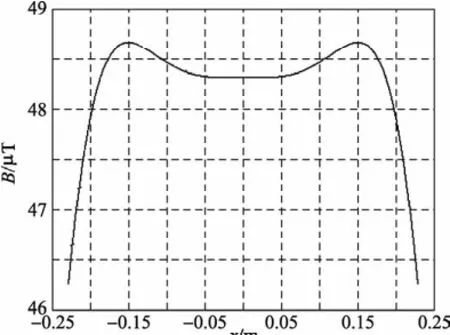
图6 圆形系统X轴上磁场分布

图7 矩形系统X＝0平面磁场分布

图8 圆形系统X＝0平面磁场分布

2）考察欲屏蔽正方体区域内磁感应强度变化。根据X＝0平面上磁场分布可知，棱边上磁感应强度变化最大，为考察正方体内磁场变化情况，分析棱边上的强度变化即可。又由于磁场具有对称性，只分析沿X轴方向的棱边。图9、图10为矩形系统和圆形系统在Y＝Z＝5 cm棱边上磁感应强度随X的变化。

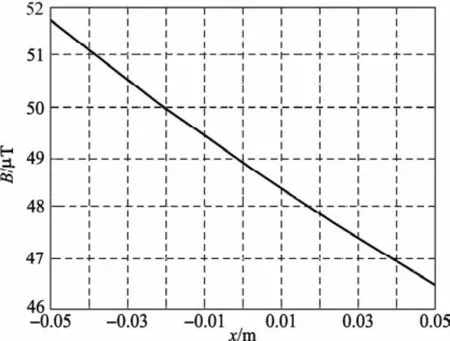
图9 矩形系统，Y＝Z＝5 cm棱边磁场分布

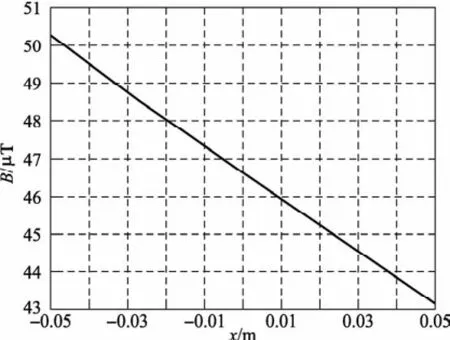
图10 圆形系统，Y＝Z＝5 cm棱边磁场分布

经验证，在Y＝Z的两个棱边上磁感应强度在X方向的变化值相同，在Y＝－Z的两个棱边上磁感应强度在X方向的变化值相同，且在Y＝Z处的磁感应强度变化值要远大于Y＝－Z处的变化值。表1给出Y＝Z的棱边上，两系统的磁感应强度变化值。

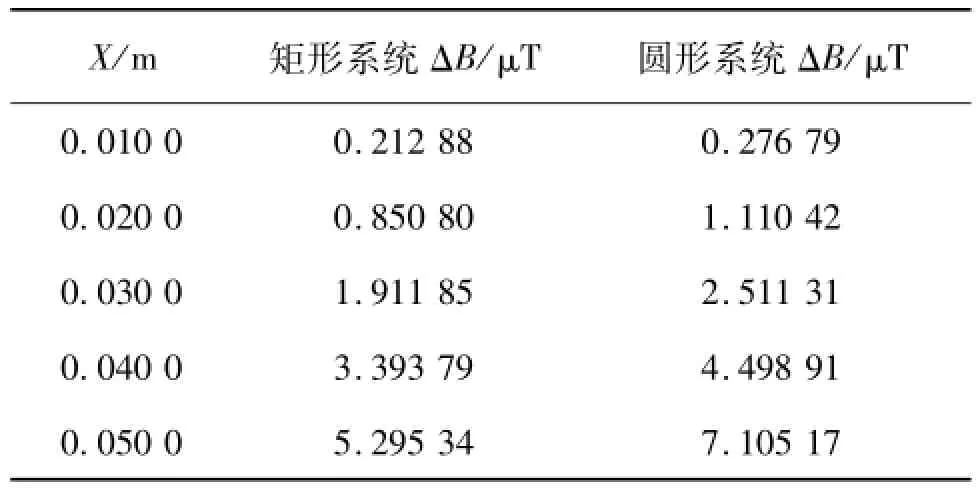
表1 正方体Y＝Z的棱边上的磁感应强度变化值

由以上数据可知，在相同边长的正方体区域内，矩形系统的磁感应强度变化要小于圆形系统，在6 cm3的立方体内矩形系统磁感应强度变化不超过2μT，圆形系统约为2.5μT，10 cm3的立方体内矩形系统磁感应强度变化不超过5.5μT，而圆形系统约为7μT。所以在所需中心10 cm3的正方体屏蔽区域内，矩形系统的均匀性要略优于圆形系统。

4 结 论

冷却和俘获原子实验中需利用磁场屏蔽系统抵消近似均匀的环境磁场。本文分析比较了矩形线圈和圆形线圈两种屏蔽系统的激励磁场分布情况，仿真结果表明，取相同参数时矩形系统激励磁场的均匀性要略优于圆形系统，且若抵消相同磁场，矩形系统所需电流较小。

事实上，线圈屏蔽系统是利用对称线圈通以相同电流，在其中心对称区域磁场叠加产生均匀磁场，其原理类似于亥姆霍兹线圈。矩形系统和圆形系统取相同边长／直径参数时，矩形线圈的覆盖范围要比圆形线圈略大，且矩形系统在中心区域产生的均匀磁场更接近于立方体。所以，在系统中心处10 cm3范围的正方体预屏蔽区域，矩形系统的效能即磁场均匀性和所需激励电流要略优于圆形系统。

文中分析的屏蔽系统均为理想矩形线圈和理想圆形线圈，实际加工时，不可能是完全理想的，如矩形线圈的拐角处为圆弧而非理想的直角，圆形线圈也难免会成为椭圆。但根据以上屏蔽系统激励原理推断，实际矩形屏蔽系统效能同样略优于实际圆形屏蔽系统。

［1］ 陆小松.基于冷原子系综的非经典关联光子源研究［D］.合肥：中国科学技术大学，2009.

［2］ Anderson M H，Ensher J R，Matthews M R，etal. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor［J］.Sience，1995，269（5221）：198－201.

［3］ ErtmerW，Blatt R，Hall JL，etal.Laser Manipulation of Atomic Beam Velocities：Demonstration of Stopped Atoms and Velocity Reversal［J］.PhysicalReviewLetters，1985，54（10）：996－999.

［4］ 赵永明，徐云飞，吴艳，等.通过补偿法获得零磁场环境［J］.浙江大学学报，2006，33（1）：44－47.

［5］ 王奎龙.激光冷却和俘获原过程控制的研究［D］.杭州：浙江大学，2008.

［6］ 邝向军.矩形载流线圈的空间磁场计算［J］.四川理工学院学报，2006，19（1）：17－20.

The Study on Com parison of EnvironmentalMagnetic Field Shielding Effectiveness of Rectangular Coiland Circular Coil

DONG Quan-lin，LIU Xue-ping，FAN Yun-qiang，XU Xiao-bin，SONG Ning-fang，ZHANG Chun-xi
（School of Instrumentation Science and Opto-electronics Engineering，Beihang University of
Aeronautics＆Asteonautics，Beijing 100191，China）

A magnetic shield system composed of threemutually perpendicular coilswas studied.Biot－Savart Law is applied to analyze and compare themagnetic field distribution of rectangular shield system and circular shield system with the help ofMatlab.The experimentdata show that the performance of rectangular shield system isslightly better than thatof the circular shield system.The conclusion can be applied in the design of atomic gyroscope，electronmicroscope and so on.

Metrology；Geomagnetic compensation；Magnetic shield；Rectangular shield system；Circular shield system

TB972

A

1000-1158（2014）05-0484-04

10．3969／j．issn．1000-1158．2014．05．16

2013-01-29；

2013-07-23

国家科技支撑计划（2006BAK03A24）

董全林（1964－），男，黑龙江泰来县人，北京航空航天大学教授，博士生导师，主要从事超显微仪器技术、惯性导航与制导的研究。dongquanlin＠buaa.edu.cn