非均匀采样正弦波形的最小二乘拟合算法

梁志国， 朱振宇

（1.北京长城计量测试技术研究所计量与校准技术重点实验室，北京100095；2.天津大学精密仪器与光电子工程学院，天津 300072）

非均匀采样正弦波形的最小二乘拟合算法

梁志国1， 朱振宇2

（1.北京长城计量测试技术研究所计量与校准技术重点实验室，北京100095；
2.天津大学精密仪器与光电子工程学院，天津 300072）

针对非均匀采样序列提出了一种四参数正弦波形曲线拟合方法。它借助于频率已知的三参数正弦曲线拟合算法实现，既可以在非均匀采样条件下获得正弦波采样序列的4个参数拟合值，也可用于均匀采样条件下正弦波形采样序列的曲线参数拟合。其特点是将幅度、频率、相位和直流分量4个参数的四维非线性最优化问题转化成频率参数的一维线性搜索和最优化问题。其优点是无需先验初值估计，具有良好的收敛性、鲁棒性，以及明确的收敛区间。仿真及实验均证明了该方法的有效性和可行性。该方法可用于解决非均匀采样和均匀采样下正弦波测量序列的参数拟合问题。

计量学；非均匀采样；正弦波；曲线拟合；参数估计；校准

1 引 言

四参数正弦波形最小二乘拟合算法是具有广泛应用价值和前景的基本算法，因而吸引了众多学者对该问题进行了广泛而深入的研究。这些研究中，多数是针对具有恒定采样间隔的均匀采样方式进行的，这也是多数数字信号处理理论和方法中的基本假设和前提［1～13］。然而，伴随着高速宽带信号的测量处理需求，非均匀采样技术开始出现。例如，以多A／D采样序列合成更高速采样序列的高速采样技术，以针对周期信号波形的取样示波器的延迟采样技术和随机采样技术等，尽管它们最终目的都是合成等效的均匀采样序列，但由于技术的不完善等因素，产生了非均匀采样效应。若仍然按照均匀采样方式进行处理，则将造成时基失真和频谱混叠。多年以来，有众多研究是专门针对这些非均匀采样导致的时基失真开始的。

另有一类现象，是在均匀采样序列中，由于瞬态干扰或短期粗大误差造成了测量序列中有部分波形严重失真和错误，以往人们处理的方式是重新测量或直接切除部分波形。人们也希望找到一种方法，在直接剔除严重错误部分后形成的“非均匀采样”序列波形仍然能够进行整体有效的参数拟合。若将它们完全按照均匀采样方式处理，将会造成额外的误差或波形失真，根本无法进行有效的参数拟合与估计。

由于正弦波形四参数拟合是一个对初始值准确度要求较高的非线性迭代过程，因而以往的四参数正弦波曲线拟合大都要求首先给出距离参数真值足够近的初始估计值，若初始值估计不够精确，则会导致迭代不收敛，或收敛到局部最优值点上，而非总体最优值点，其收敛区间大都不够明确。由于均匀采样条件下正弦波形参数的初始值估计可以有很多方法，如FFT方法、峰值检测法、平均值法等，且足够准确，因此，以往的四参数正弦波拟合方法主要是针对均匀采样条件下的正弦波形序列，在非均匀采样序列中，初始值参数估计将面临更大困难，甚至无法进行有效估计，导致它们很多时候无法适应非均匀采样正弦波序列的最小二乘拟合要求。

本文后续工作，将主要针对上述这些非均匀采样正弦波序列的最小二乘拟合开展研究，以寻找出一种适合非均匀采样正弦序列波形参数拟合的最小二乘算法。

2 三参数正弦波形的最小二乘拟合算法

2.1 三参数正弦曲线拟合法［14］

设理想正弦波形为：

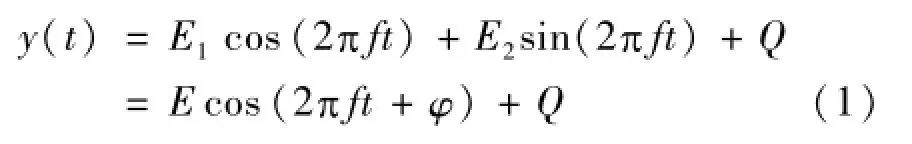
式中：E为正弦波形幅度；f为正弦波形频率；φ为正弦波形初始相位角；Q为正弦波形信号的直流分量值。

数据记录序列为已知时刻t1，t2，…，tn的采集样本y1，y2，…，yn。三参数正弦曲线拟合过程，即为输入信号的频率f已知，选取或寻找A1、B1、C，使下式所述残差平方和ε最小：

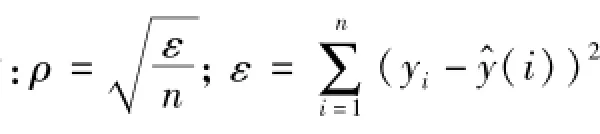
2.2 问题讨论

上述三参数正弦曲线拟合过程，是已知信号频率f下进行的。

不失一般性，设给定信号测量序列的数字角频率为w，而不是ω。则，使用10个周期的正弦波形序列，按上述三参数正弦曲线拟合得如图1所示归一化误差ρ／E与数字角频率比w／ω关系曲线波形。图2为图1的局部细化。

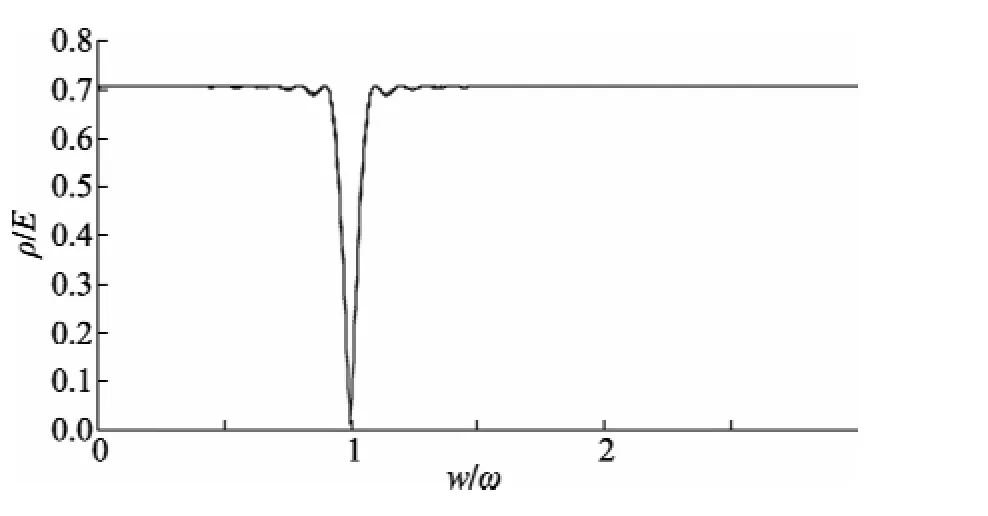
图1 多周期时归一化误差ρ／E与数字角频率比w／ω关系曲线

由于数字角频率与频率存在式（7）所述确定关系，故拟合过程中的数字角频率比也是拟合过程中的信号频率比，完全可以代表其频率拟合特征。

其中，ω＝2π／1000；E＝100；Q＝0；φ分别取0°、40°、80°、120°、160°、200°、240°、280°、320°、360°；以w代替ω进行三参数拟合。

从图1及其局部细化曲线波形图2可见，对于信号为数字角频率ω的正弦曲线，三参数最小二乘拟合法在ω±ω／10（即［0.9ω，1.1ω］）范围内极值存在且唯一，幅度和相位的变化不影响其ρ／E的变化规律，可在ω±ω／10范围内通过对ω的一维搜索找出该极值点。

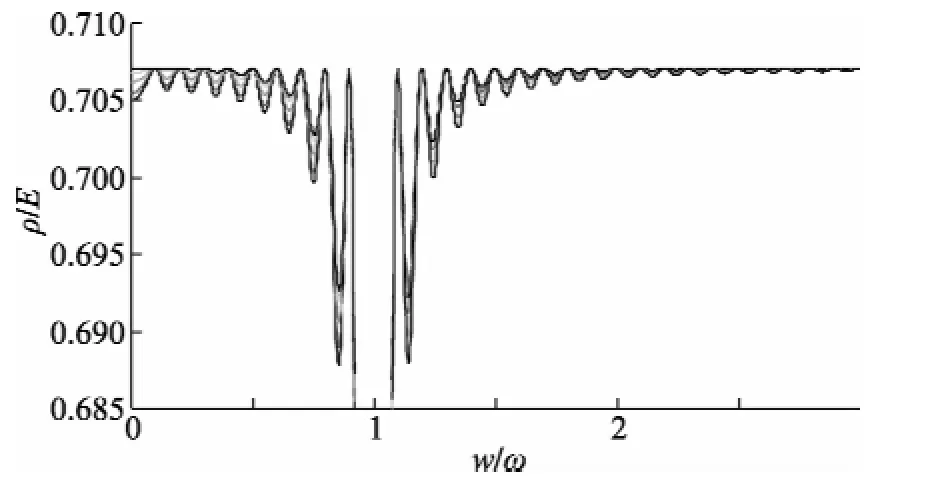
图2 多周期时归一化误差ρ／E与数字角频率比w／ω关系曲线（局部）

在全频率范围内，幅度E的变化基本上不影响ρ／E随w／ω的变化时极值点出现的位置和幅度；相位变化也不影响ρ／E随w／ω变化时极值点出现的位置，而只改变非ω频率处各个ρ／E极小值的大小，对各极大值则无影响。

从变化p值等参数的多组仿真运算不难看出，一般情况下，对于含有p个周期的频率为f的正弦波形序列，按上述三参数正弦曲线拟合有如下规律：

（1）在f±f／p（即［f－f／p，f＋f／p］）范围内，ρ／E的极值存在且唯一，极值点就是f频率点；

（2）幅度和相位的变化不影响ρ／E的变化规律，但初始相位φ的变化将影响ρ／E的幅度值；

（3）可以通过f的初始估计值以及p值估计和判断四参数正弦波曲线拟合算法的收敛区间［f－f／p，f＋f／p］；

（4）可在f±f／p范围内通过对f的一维搜索找出ρ／E的极值点！并且，该极值点处的最小二乘拟合结果就是四参数最小二乘正弦波拟合结果。

3 四参数正弦波形的最小二乘拟合算法

3.1 原理过程

假设待估计的正弦波频率目标值为f0，待估计的正弦波采样序列所含信号周期个数为p；则有，最大频率差值Δfmax＝f0／p＝1／（tn－t1），在区间［f0－Δfmax，f0＋Δfmax］内的任意频率f下，残差平方和ε（f）的极值存在且唯一！这样，便将四参数正弦波曲线拟合中，对幅度、频率、相位、直流分量4个参数的四维非线性搜索，变成了对频率分量f造成的ε（f）的一维线性搜索，可保证在区间［f0－Δfmax，f0＋Δfmax］内，用三参数拟合法实现的四参数正弦曲线拟合过程绝对收敛。该四参数拟合过程如下：

（1）设定拟合迭代停止条件为he；he为用于判定迭代残差增量的一个非常小的小数值，例如可令he＝10－15或更小。

否则，重复（4）～（6）的过程。

3.2 收敛性问题

四参数正弦曲线拟合是一个迭代过程，也有收敛性问题。如上所述，对于含p个信号周期的测量序列的情况，如图1所示，四参数正弦曲线拟合的绝对收敛区间为［f0（1－1／p），f0（1＋1／p）］；其中，f0为信号的真实频率。

在该绝对收敛区间之外，当p≥2时，首先，可以对测量序列的有效值Erms进行预估计，

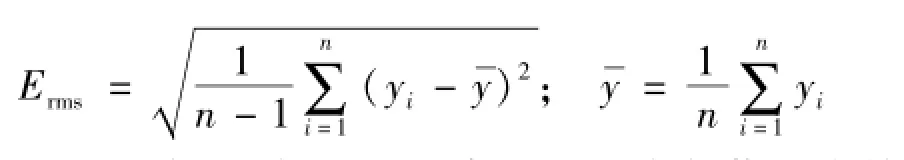
不失一般性，假设正弦序列的噪声与信号有效值幅度之比为N／S≪1，即噪声功率远小于信号功率，则可选取判据hd取值满足N／S＜hd＜1。

然后，变化f在（0，＋∞）区间内搜索从ρ（f）／Erms＞hd变化到ρ（f）／Erms＜hd处的频率点fd，根据在fd附近ρ（fd）的变化规律可以判断：

当导数ρ′（fd）＜0，fd＜f0，可令fL＝fd；

当导数ρ′（fd）＞0，fd＞f0，可令fR＝fd。

这样，便寻找出落在绝对收敛区间内且包含f0的迭代区间［fL，fR］，使用前述方法可获得绝对收敛的四参数正弦拟合结果。

采取辅助判据hd这样一种措施后，可将本文所述四参数正弦拟合方法的频率绝对收敛区间拓展到（0，＋∞），从而可在任何情况下都获得收敛结果。

4 仿真实验验证

选取测量范围－5V～＋5 V，幅度4 V，直流分量0 V，初始相位100°，频率6 Hz，均匀采样速率8 kSa／s，采样间隔τ0＝0.125 ms，采样序列长度n＝4 000的采样序列，约含3个波形周期。使用本文上述四参数拟合算法进行正弦参数估计，获得拟合曲线与采样曲线波形如图3所示，两者之差异曲线如图4所示。其拟合参数如表1所示。

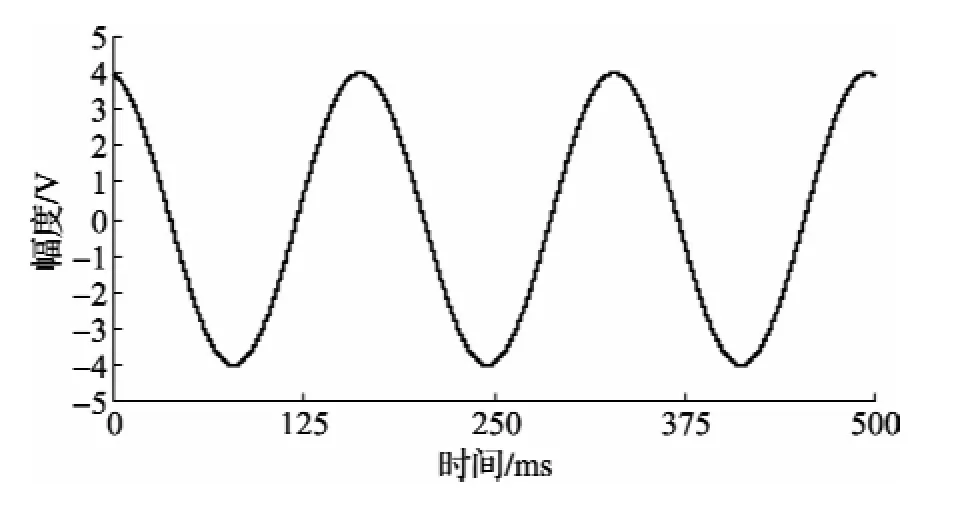
图3 正弦拟合曲线y＾（i）与均匀采样曲线yi

令正弦波模型参数不变，使用随机采样间隔进行序列采样，获得采样序列并按照本文上述方法进行正弦波曲线拟合，得采样序列曲线及其拟合曲线分别如图5～图8所示。

图4 正弦拟合曲线与均匀采样曲线差异yi－y＾（i）

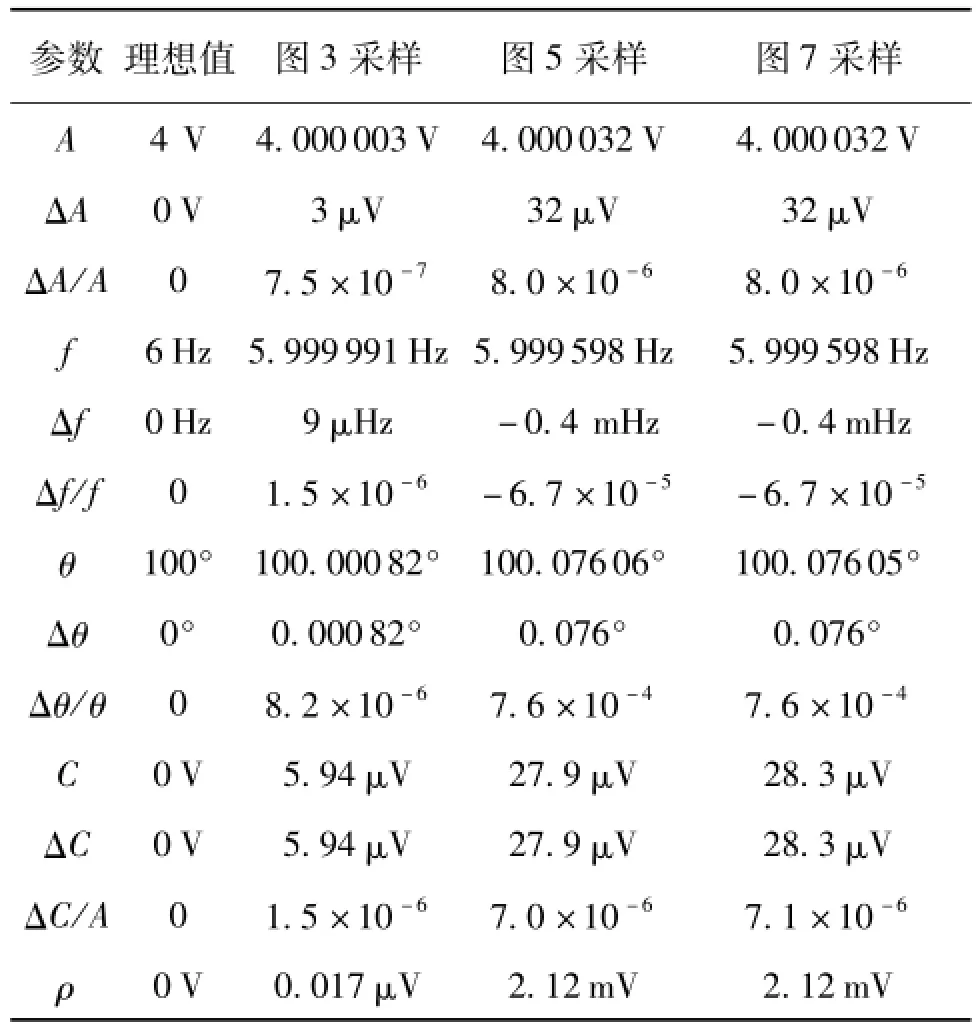
表1 正弦波采样序列波形参数拟合结果

其中，图5为波形长度约为6个周期的非均匀采样序列曲线及其拟合曲线，其采样间隔为（RND－0.4）×20τ0。τ0＝0.125 ms。其中，RDN为在［0，1］内均匀分布的随机数。可见由于采样间隔呈非均匀随机变化状态，按照等间隔均匀采样模式绘制的曲线图5，其中的“正弦波形”已经变化非常大。若仍然按照均匀采样间隔处理，将无法获得有效拟合结果，甚至会拟合失败。图6为拟合曲线与采样序列之差异曲线。可见两者拟合得非常好。相应拟合参数见表1。由表1可见，非均匀采样条件下正弦曲线拟合误差要略大于均匀采样条件下，但差异不太大，造成差异的原因有待于进一步研究。

图7为图5的测量曲线不经过时间从小到大的排序直接进行四参数拟合获得的拟合结果与测量序列曲线，图8为此情况下两者之间的差异曲线，拟合参数如表1所示。由表1数据及图7和图8可见，未经时间顺序排序的采集波形拟合参数与经过排序后再执行拟合的结果没有本质差异。

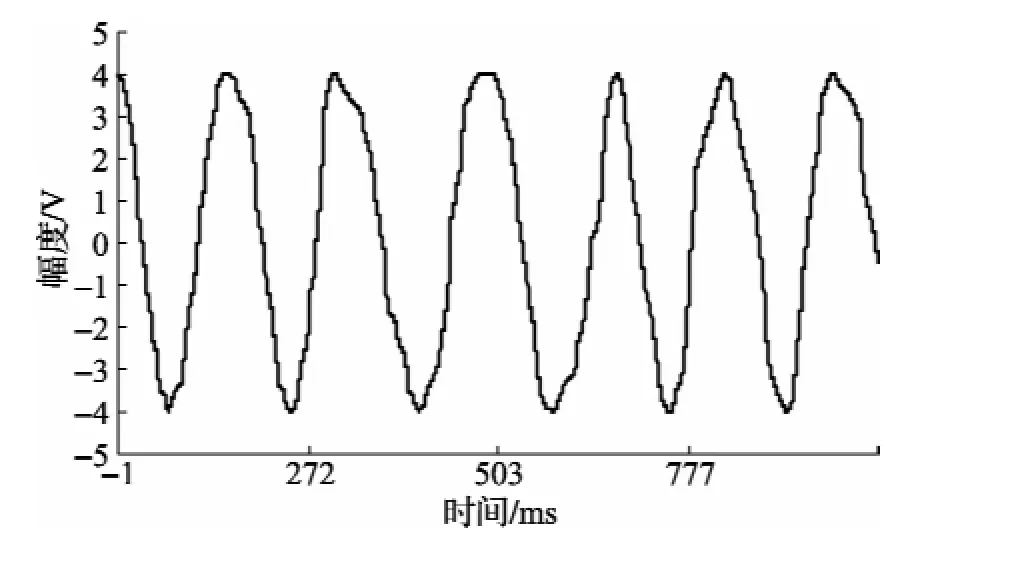
图5 正弦拟合曲线y＾（i）与非均匀采样曲线yi（先进行时间排序）

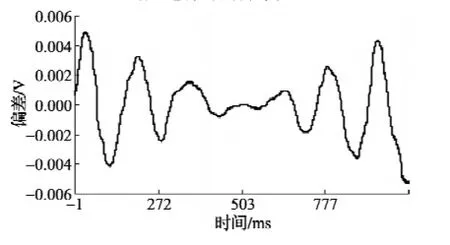
图6 正弦拟合曲线与非均匀采样曲线差异yi－（先进行时间排序）

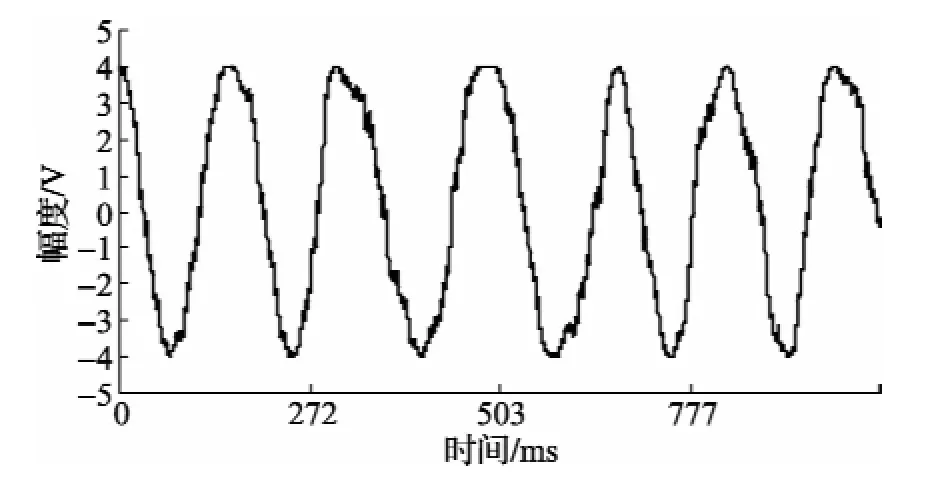
图7 拟合曲线）与非均匀采样曲线yi（未进行时间排序）

5 实验验证

用FLUKE5700多功能校准器作激励源，给出幅度8.0000V的正弦电压信号，频率10.000Hz，以北京阿尔泰公司ART2001型数据采集系统执行采集，其A／D位数12 Bit，工作量程±10 V，采样速率5000 Sa／s，采集数据个数2000点。

使用上述四参数正弦波拟合方法获得其正弦波形幅度为8.016459 V，频率为10.00005 Hz，相位为－17.9767°，直流分量为0.483 mV。残差有效值ρ＝2.21 mV。其测量序列波形及拟合曲线如图9所示，测量序列波形与拟合曲线之差如图10所示。

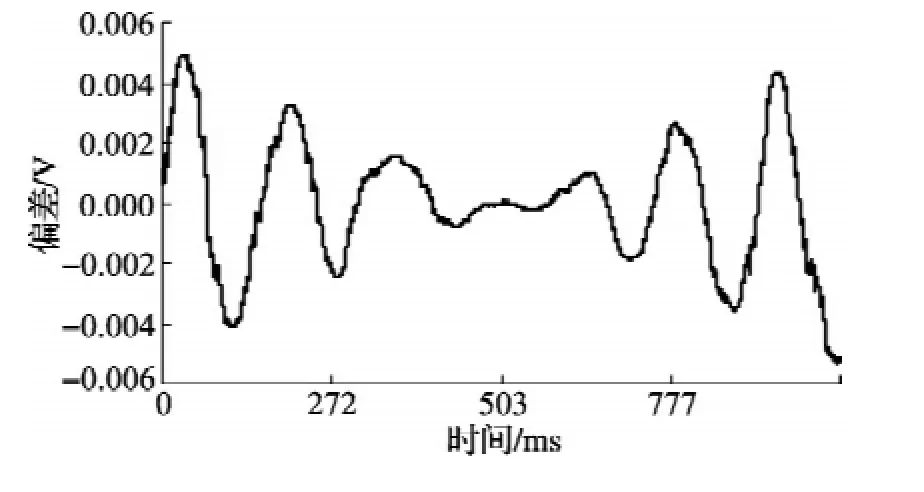
图8 拟合曲线与非均匀采样曲线差异yi－（未进行时间排序）

图9 拟合曲线）与均匀采样曲线yi

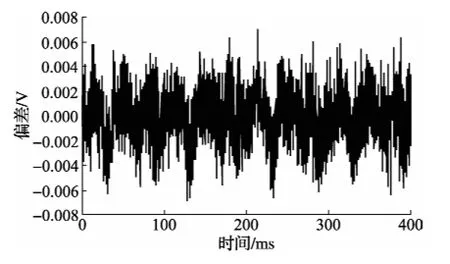
图10 拟合曲线与均匀采样曲线差异yi－

将上述测量曲线波形截取三段后，变成非均匀采样序列，使用上述四参数正弦波拟合方法获得其正弦波形幅度为8.016445V，频率为10.00003Hz，相位为－17.9755°，直流分量为0.443mV。残差有效值ρ＝2.22 mV。其测量序列波形及拟合曲线如图11所示，测量序列波形与拟合曲线之差如图12所示。

6 讨 论

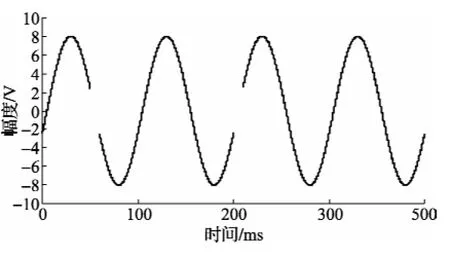
图11 拟合曲线与非均匀采样曲线yi

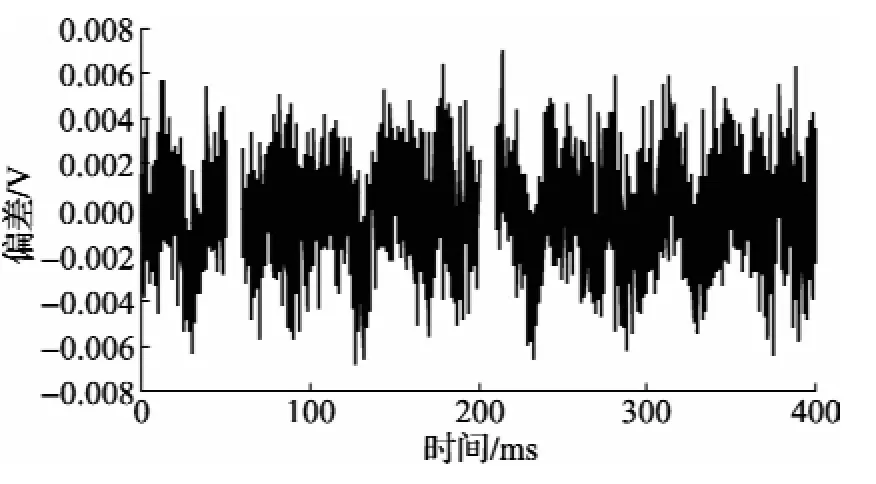
图12 拟合曲线与非均匀采样曲线差异yi－

从上述仿真和实际实验结果可见，本文所述正弦波拟合测量方法可以用于非均匀采样正弦波形参数的测量估计，并可以给出幅度、频率、相位、直流分量等基本信息参量。其最大特点是针对同时具有采样幅度信息和采样时间信息的正弦波序列，不论其采样间隔是否均匀，均可以获得有效收敛结果，特别是针对均匀采样序列剔出一段异常波形情况，在实际工作中时有发生，而本来希望获得均匀采样序列，但由于周期过长以及测量过程不完善等因素，使得采样序列变成非均匀采样序列的情况比比皆是。对于随机采样情况，甚至时间排序出现前后颠倒的情况下，本文方法依然可以有效获得拟合结果，体现出算法良好的收敛性和鲁棒性，可直接用于解决上述范畴内的工程技术问题。

仿真实验表明，与均匀采样条件相比，非均匀采样序列正弦拟合误差要略大一些。实际实验中，两者的差异不明显。

7 结 论

综上所述，本文提出了非均匀采样条件下正弦波测量序列四参数拟合的一种方法，给出了详细过程和收敛区间，并分别在随机间隔采样和非随机间隔采样两种条件下给出了比较结果。结果表明，本文所述方法具有良好收敛性和鲁棒性，仅要求已知采样序列和每个采样点的时刻，没有任何其它先决条件要求，是一种表现良好的正弦参数拟合方法，可直接用于非均匀采样条件下正弦波形的参数拟合。

［1］ Kuffel J，M cComb T R，Malewski R.Comparative Evaluation of Computer Methods for Calculating the Best-Fit Sinusoid to the Digital Record of a High-Purity Sine Wave［J］.IEEETransactionsonInstrumentationand Measurement，1987，36（2）：418－422.

［2］ McComb T R，Kuffel J，Le Roux B C.A Comparative Evaluation of Some Practical Algorithms Used in the Effective Bits Test of Waveform Recorders［J］.IEEE TransactionsonInstrumentationandMeasurement，1989，38（1）：37－42.

［3］ Jeng Y C.High precision sinusoidal frequency estimator based on weighted least square method［J］.IEEE TransactionsonInstrumentationandMeasurement，1987，36（1）：124－127.

［4］ Deyst J P，Souders T M，Solomon O.Bounds on Least-Squares Four-Parameter Sine-Fit Errors Due to Harmonic Distortion and Noise［J］.IEEETransactionson InstrumentationandMeasurement，1995，44（3）：637－642.

［5］ Zhang JQ，Zhao Xinmin，Hu Xiao，etal.Sine wave fit algorithm based on total least-squares method with application to ADC effective bitsmeasurement［J］.IEEE transactionsonInstrumentationandMeasurement，1997，46（4）：1026－1030.

［6］ Handel P.Properties of the IEEE-STD-1057 Four-Parameter Sine Wave Fit Algorithm［J］.IEEE TransactionsonInstrumentationandMeasurement，2000，49（6）：1 189－1193.

［7］ 田社平，王坚，颜德田，等.基于遗传算法的正弦波信号参数提取方法［J］.计量技术，2005，（5）：3－5.

［8］ 梁志国，朱济杰，孟晓风.四参数正弦曲线拟合的一种收敛算法［J］，仪器仪表学报，2006，27（11）：1513－1519.

［9］ 梁志国，孟晓风.残周期正弦波形的四参数拟合［J］.计量学报，2009，30（3）：245－249.

［10］ Bilau T Z，Megyeri T，Sárhegyi A，etal.Fourparameter fitting of sinewave testing result：Iteration and convergence［J］.ComputerStandards＆Interfaces，2004，26（1）：51－56.

［11］ Palfi V，Kollar I.Acceleration of the ADC Test With Sine-Wave Fit［J］.IEEETransactionsonInstrumentation andMeasurement，2013，62（5）：880－888.

［12］ Chen K F.Estimating Parameters of a Sine Wave by Separable Nonlinear Least Squares Fitting［J］.IEEE TransactionsonInstrumentationandMeasurement，2010，59（12）：3214－3217.

［13］ Sárhegyi A，Kollár I.Robust Sine Wave Fitting in ADC Testing［C］／／Proceedings of the IEEE Instrumentation and Measurement Technology Conference，2006.Sorrento，Italy，2006，24－27.

［14］ IEEE Std 1057-1994.IEEE standard for digitizing waveform recorders［S］.1994.

The Sinewave Fit Algorithm Based on Total Least-square Method w ith Non-uniform Samp ling

LIANG Zhi-guo1， ZHU Zhen-yu2
（1.Changcheng Institute of Metrology and Measurement，Beijing 100095，China；
2.College of Precision Instrument and Opto-electronics Engineering，Tianjin University，Tianjin 300072，China）

Aiming at the non-uniform sampling series，a four-parameter sine wave curve-fitmethod is introduced.It is based on the three-parameter sine wave curve-fit method with frequency known.It can attain the four-parameter of sinusoidal curve-fit results with both the uniform sampling series and the non-uniform sampling series.The speciality of the arithmetic is that it turns the optimization of four parameters（amplitude，frequency，phase and offset）into the optimization of one parameter（only frequency），and without any original parameter estimation.Themethod has excellent convergence，good robustness，and clearly convergence interval.The validity and feasibility are proved by both simulation and experiments，thismethod can be applied to the four-parameter sinewave curve-fitwith non-uniform sampling series.

Metrology；Non-uniform sampling；Sinusoidal；Curve-fit；Parameter estimation；Calibration

TB973

A

1000-1158（2014）05-0494-06

10．3969／j．issn．1000-1158．2014．05．18

2013-05-17；

2013-09-23

梁志国（1962－），男，黑龙江巴彦人，博士，北京长城计量测试技术研究所研究员，主要研究方向为数字化测量与校准、模式识别、动态校准、精确测量。Lzg304＠sina.com