一类模糊合作博弈及其核心

王锋叶，黄志勇，尚有林，陈 鹏

（河南科技大学数学与统计学院，河南洛阳 471023）

一类模糊合作博弈及其核心

王锋叶，黄志勇，尚有林，陈 鹏

（河南科技大学数学与统计学院，河南洛阳 471023）

基于经典的具有无限多局中人的合作博弈，定义了具有Choquet积分形式的模糊合作博弈，讨论了所定义模糊合作博弈的单调性、超可加性及缺原子性等性质，证明了这类模糊合作博弈的核心的存在性及其表示形式。

模糊合作博弈；Choquet积分；核心

0 引言

由参与合作博弈的局中人的多少，合作博弈可分为n人合作博弈（局中人有限）与局中人无限的合作博弈。在利用n人合作博弈进行经济分析时，有限局中人的合作博弈不能很好的解决自由市场中的很多博弈问题，如微观经济学中的安全经济市场，这就需要一种大量局中人参与的博弈，称为局中人无限的合作博弈，其局中人的集合用无穷集合表示，博弈用定义在无穷集合上的集函数来表示。

当合作博弈中的局中人以一定程度参与某个联盟，且可参与多个联盟时，这种合作博弈就是模糊合作博弈。目前，对模糊合作博弈的研究主要是n人合作博弈。文献［1］提出了一个模糊环境下的Shapley函数，并证明了这个Shapley函数是一个模糊总体单调分配函数。文献［2］基于Hukuhara差，给出了特征函数模糊及联盟模糊的n人博弈的Shapley函数形式。文献［3－4］从改进联盟结构的角度研究博弈问题，得到了联盟模糊的合作博弈的Shapley函数的简单表示。文献［5］定义了一类特殊的n人模糊联盟，并对其模糊核心的存在性问题进行了研究。文献［6］给出了具有多线性拓展形式的模糊合作博弈的Shapley函数，并对其唯一性及性质进行详细的研究。文献［7］讨论了支付是模糊数情形的合作博弈的Shapley值，构造了模糊Shapley值隶属函数。目前，对局中人无限的模糊合作博弈的研究则很少。文献［8］基于三角模测度对局中人无限的模糊合作博弈的Aumann-Shapley值的存在性及表示形式进行了详细的研究。文献［9－10］也对局中人无限的模糊合作博弈的性质进行了研究。

本文利用经典的合作博弈定义了一类特殊的局中人无限的模糊合作博弈，并对其具有的一些性质进行了证明，最后，研究了这类特殊模糊合作博弈的核心存在性及表示形式。

1 基本概念

设可测空间（X，C），其中，X表示局中人的集合，C是X的所有子集组成的σ-代数，表示由局中人组成的所有可能联盟的全体。可测空间（I，β）是与（X，C）同构的可测空间，其中，I为区间［0，1］，β是由［0，1］的子集构成的Borel集族。一个具有无限局中人的合作博弈（或具有连续统局中人的合作博弈）v是定义在可测空间（X，C）上的实值集函数，即v：C→ℝ，满足v（Ø）＝0。

定义1［11］设v为具有无限多局中人的合作博弈，若对任意的A∈C，v（A）≠0，总存在A的子集B∈C，使得v（B）∉｛0，v（A）｝，则称v是缺原子的。

所有缺原子博弈的集合记为NA，所有单调缺原子博弈的集合记为NA＋，所有单调缺原子博弈的幂生成的空间记为pNA。

定义2［11］设v为具有无限多局中人的合作博弈，若对任意A、B∈C，且A∩B＝∅，有v（A∪B）≥v（A）＋v（B），则称v是超可加的。

定义3［11］设v*是由v扩张而成的博弈，满足v*（χA）＝v（A），这里，A∈C，χA是A的特征函数。若对所有的α∈［0，1］，A∈C，有v*（αχA）＝αv（A），则称博弈v是一阶齐次的。

定义4［11］设v为具有无限多局中人的合作博弈，如果存在有限可加函数m：C→ℝ，使得m（X）＝v（X），m（A）≥v（A），A∈C，则称函数m为博弈v的一个核心。

博弈v的所有核心的集合记为Core（v）。

引理1［11］设v∈pNA，且具有超可加性与一阶齐次性，则博弈v存在唯一的核心。

对于具有无限多局中人的合作博弈，当局中人以一定程度参与某个联盟，这种博弈称为模糊博弈，联盟称为模糊联盟，利用将（X，C）映射到（I，β）的可测函数A表示。对任意的x∈X，A（x）表示局中人x参与模糊联盟A的程度，也是x对模糊集A的隶属度。对任意的α∈［0，1］，模糊集A的水平集为Aα＝，X的所有在［0，1］上可积的模糊集的全体记为F（X）。

一个具有无限局中人的模糊合作博弈v定义为将F（X）映射到ℝ且满足v（φ）＝0的集函数，G（X）表示所有模糊博弈的集合。

本文中，两个模糊集的交与并定义为：

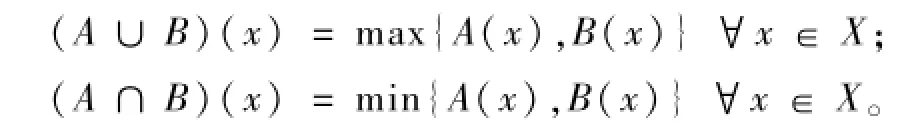
定义5设v∈G（X），若对任意的A∈F（X），v（A）≠0，总存在A的子集B∈F（X），使得v（B）∉｛0，v（A）｝，则称v是缺原子的。

定义6设v∈G（X），若对任意的A、B∈F（X），且A∩B＝∅，有v（A∪B）≥v（A）＋v（B），则称v是超可加的。

2 具有Choquet积分形式的模糊合作博弈

定义7 设X为局中人的集合（相互作用组成模糊联盟A），A是X的模糊子集且其水平集为Aα＝那么一个博弈v∈G（X）称为具有Choquet积分形式的模糊合作博弈，如果满足

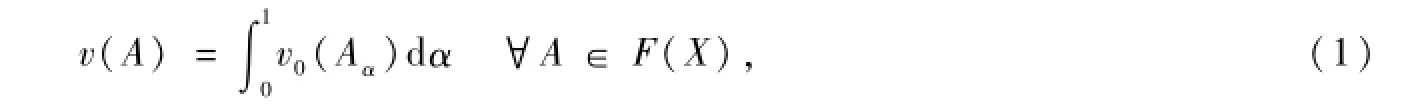
其中，等式右端的积分是Lebesgue积分；v0是定义在X上经典单调博弈，记v0的全体集合为G0（X），具有Choquet积分形式的模糊合作博弈的全体为GC（X）。

由Choquet积分的定义知，式（1）的右端积分是函数A在X上关于v0的Choquet积分［12－13］，即

特别地，当A为经典集合时，v（A）＝v0（A），即经典博弈v0是具有Choquet积分形式的模糊博弈的特殊情形，它们之间的关系是一一对应的。从而称v0为相应于v的经典博弈。

当v0为经典测度即可列可加测度且A在［0，1］上可积，那么式（2）中的Choquet积分就为A在［0，1］上关于测度v0的Lebesgue积分，记这类具有Choquet积分形式的模糊合作博弈的全体为GL（X）。显然，GL（X）⊂GC（X）。

性质1若v0∈G0（X）是超可加的，则模糊博弈v∈GC（X）也是超可加的。

证明对任意的模糊集A、B∈F（X），A∩B＝∅，α∈［0，1］有：（A∪B）α＝Aα∪Bα。从而，

所以，模糊博弈v∈GC（X）是超可加的。

性质2若v0∈G0（X）是单调的，则v∈GC（X）也是单调的。

3 具有Choquet积分形式的模糊博弈的核心

定义8设有限可加函数m：F（X）→ℝ，若

则称m为模糊博弈v的一个核心，v的所有核心的集合记为Core（v）。

定理1设v∈GL（X）是具有Choquet积分形式的模糊博弈，定义有限可加函数m：F（X）→ℝ为

其中，m0是经典博弈v0∈G0（X）的一个的核心，v0是相应于v∈GL（X）的经典博弈，则m是博弈v∈GL（X）的一个核心。

证明先证m是有限可加的。设模糊集A、B∈F（X），且A∩B＝∅，则对任意的α∈［0，1］，Aα∩Bα＝∅。因为m0是有限可加的，所以，对任意的α∈［0，1］，有

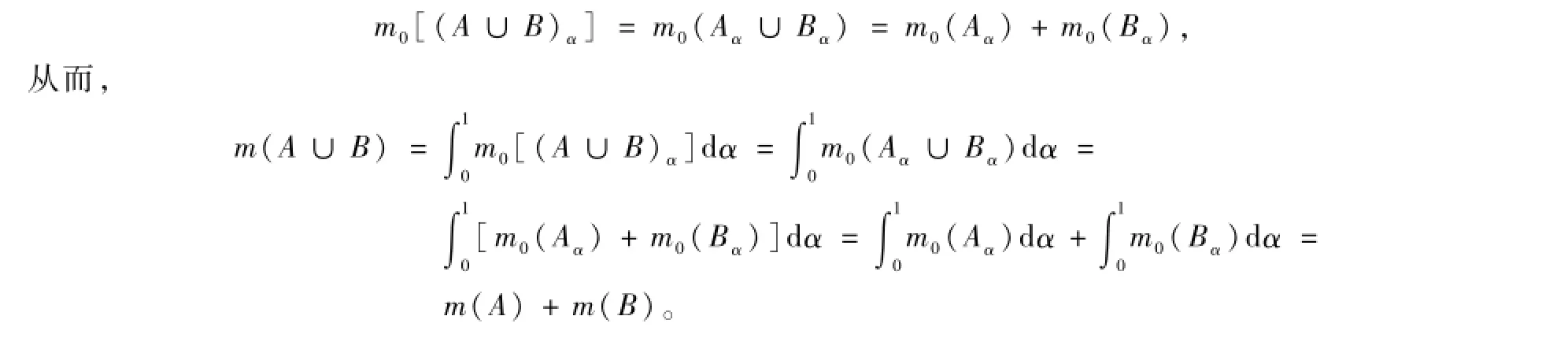
即m是有限可加的。

下证m是v的核心。

因为m0是博弈v0∈G0（X）的一个核心，则由核心的定义知m0（X）≤v0（X），又因为对任意的α∈［0，1］，有

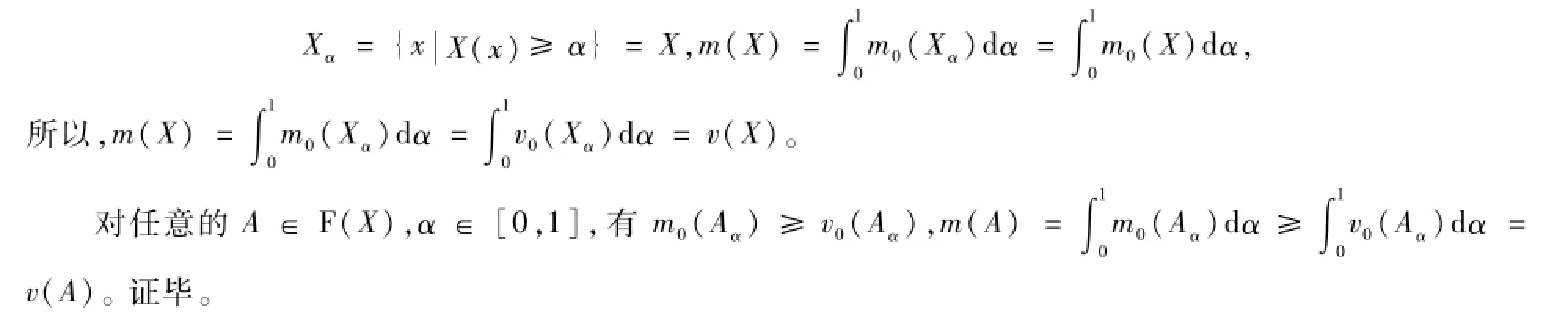
定理1表明：若经典博弈是可列可加的，且核心存在，则对应的具有Choquet积分形式的模糊合作博弈的核心也存在，且可用经典博弈的核心的Lebesgue积分形式表示。

定理2设v∈GL（X），与v相应的经典博弈v0∈pNA且具有超可加性与一阶齐次性，则v∈GL（X）存在唯一的核心。

证明由引理1知，博弈v0存在唯一的核心m0。又由定理1及v与v0的一一对应性知，与v0对应的模糊博弈v∈GL（X）也存在核心m，且

4 结论

本文定义了具有Choquet积分形式的具有无限多局中人的模糊合作博弈，讨论了这类博弈的超可加性、单调性及缺原子性，证明了基于经典测度的具有Choquet积分形式的模糊合作博弈的核心存在性及其积分表示形式。对本文所定义的模糊合作博弈，还可进一步研究其值的存在性及其与核心之间的关系等问题。

［1］ Borkotokey S.Cooperative Games with Fuzzy Coalition and Fuzzy Characteristic Functions［J］.Fuzzy Sets and System s，2008，159：138－151.

［2］ Yu X H，Zhang Q.An Extention of Cooperative Fuzzy Games［J］.Fuzzy Sets and Systems，2010，161（11）：1614－1634.

［3］ Li S J，Zhang Q.The Measure of Interaction among Players in Games with Fuzzy Coalitions［J］.Fuzzy Sets and Systems，2008，159（2）：119－137.

［4］ Li S J，Zhang Q.A Simplified Exp ression of the Shapley Function for Fuzzy Game［J］.European Journal of Operational Research，2009，196（1）：234－245.

［5］ Yu X H，Zhang Q.The Fuzzy Core in Games with Fuzzy Coalitions［J］.Journal of Computational and Applied Mathematics，2009，230（1）：173－186.

［6］ Meng F Y，Zhang Q.The Shapley Function for Fuzzy Cooperative Games with Mu ltilinear Extetion Form［J］.Applied Mathematics Letters，2010，23：644－650.

［7］ 陈雯，张强.模糊合作对策的Shapley值研究［J］.管理科学学报，2006，9（5）：50－55.

［8］ Butnariu D，K lemen E P.Triangular Norm-based Measures and Games with Fuzzy Coalitions［M］.Dordrecht：Kluwer Academic Pub lishers，1993.

［9］ 黄志勇，王锋叶，冯爱芬.关于可加模糊集函数的一种分解［J］.河南科技大学学报：自然科学版，2007，28（2）：78－81.

［10］ 黄志勇，王锋叶，郭海刚.关于T-∞测度的一些注记［J］.河南科技大学学报：自然科学版，2009，30（4）：87－89.

［11］ Aumann R J，Shapley L S.Values of Non-atomic Games［M］.New Jersey：Princeton University Press，1974.

［12］ Aubin J P.Coeur et Valeur des Jeux FlousàPaiements Latéraux［J］.Comp tes Rendus Hebdomadaires des Séances de 1＇Académ ie des Sciences，1974，279-A：891－894.

［13］ Aubin JP.Coeur Equilibres des Jeux Flous Sans Paiements Lateraux［J］.Comp tes Rendus Hebdomadaires des Seances de 1’Academie des Sciences，1974，279-A：963－966.

O225

A

1672－6871（2014）01－0075－04

国家自然科学基金项目（10971053）；河南省教育厅自然基金项目（12B110007）

王锋叶（1979－），女，山西运城人，讲师，博士，研究方向为模糊决策，博弈论.

2012－12－04