浅析数学方法在中学数学解题过程中的应用*

张鸿超

(呼伦贝尔学院数学科学学院，内蒙古呼伦贝尔021008)

浅析数学方法在中学数学解题过程中的应用*

张鸿超

(呼伦贝尔学院数学科学学院，内蒙古呼伦贝尔021008)

本文通过对中学解题过程中一般数学方法应用的探究，帮助学生自觉地运用数学方法指导解题过程，形成解决数学问题的有效策略。

数学方法;应用;中学数学

尽管中学数学教材中大量的优秀例题、习题，都蕴涵着丰富的数学方法，但在中学，数学方法仍是一个隐性的知识系统。因此，对数学方法相关内容的揭示会更有助于提高学生空间想象能力、逻辑思维能力、数学应用能力和探索创新能力，使学生把学习数学知识和培养能力有机联系起来，更好地提高个体的思维品质，培养更多创新型人才。

1 中学数学解题过程中常用的几种数学方法

1．1普通归纳法(不完全归纳法)

所谓普通归纳法(不完全归纳法)，就是对一类事物部分特殊事项加以抽象提高，通过分析、研究、推理得出一般属性和规律。其特点是:

(1)以一定的事实做为基础，所判断的范围小于结论应当判断的范围。

例如，多边形内角和的求和公式就是通过求得部分多边形的内角和，然后发现规律进而归纳得出n边形内角和的。

从每个多边形的一个顶点引出所有的对角线，四边形会被分成2个三角形，五边形会被分成3个三角形，六边形会被分成4个三角形，……，十二边形会被分成10个三角形。于是便发现所分得的三角形的个数总比它的边数少2。而每个三角形的内角和是180°，那么，n边形的内角和显然为(n－2)× 180°。

(2)得出的结论可能不正确。

例如，对“函数式y=x2+x+41中，x取任何非负整数，y都是质数”的判断时，通过个别计算我们发现，当自变量x取0，1，2，3，……，38，39时，得出y的值为41，43，47，53，…，1601，这些数都是质数，于是归纳得出x取任何非负整数，y都是质数的结论。但这个结论却是个错误的结论。因为当x=40时，得出y的值为1681，而1681能被1和它本身整除外，还能被41整除，显然y不是质数，而是合数了。

(3)得到的结论是否正确，需要经过理论的证明和实践的检验。

例如，1+8=9，

即13+23=32=(1+2)2

1+8+27=36，

即13+23+33=62=(1+2+3)2，

1+8+27+64=100，

即13+23+33+43=102=(1+2+3+4)2

……

由此，我们可以推断得出

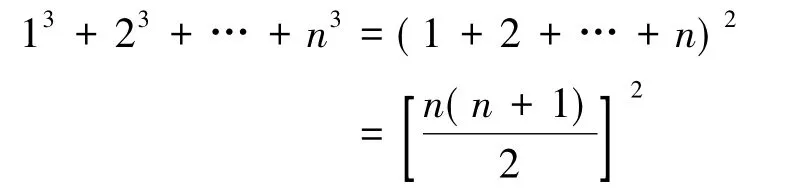
用数学归纳法可以证明，这个结果是正确的。

尽管普通归纳法(不完全归纳法)的结论不是完全可靠，但在数学研究和应用中，却有着十分重要的意义。

一是，在基础知识有限的情况下为了暂且接受其真实性，常常用普通归纳法(不完全归纳法)给出。这样的处理方法，在理论上是虽然存在缺陷，但就整体认知结构而言是合理的，既合乎认识规律，也有助于人们从具体的事例中发现一般规律。

二是，利用普通归纳法(不完全归纳法)，恰当地考察数学问题的某些特殊情形，可以帮助我们由问题的特殊性认识其一般性，探明到解决问题的方向，寻求到正确的解题路径。

三是，通过普通归纳法(不完全归纳法)探求结论，可以给人们提供一定的信息，帮助人们发现和提出新问题，丰富数学研究内容，推动数学的发展。

1．2数学归纳法

所谓数学归纳法，一般地，证明一个与自然数n有关的命题P(n)，有如下步骤:

(1)证明当n取第一个值n0时命题成立。n0对于一般数列取值为0或1，但也有特殊情况;

(2)假设当n=k(k≥n0，k为自然数)P(k)命题成立，证明当n=k+1时命题也成立。

综合(1)(2)，对一切自然数n(≥n0)，命题P(n)都成立。

②假设n=k时，等式成立，即:

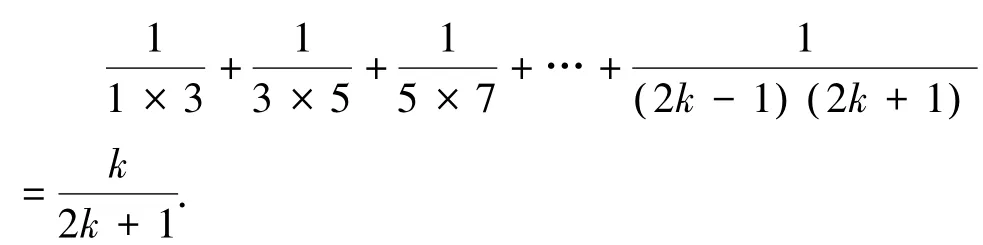
那么当n=k+1时，有:

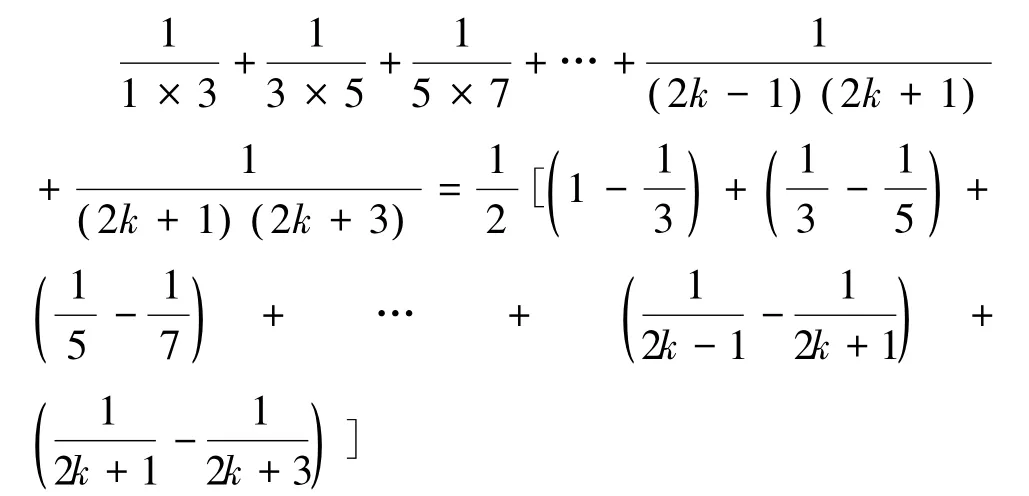
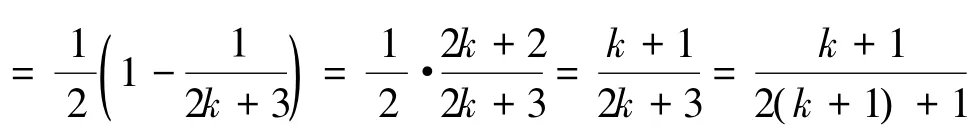
即当n=k+1时，原式也成立．

根据①、②可得对一切自然数n原式都成立．

上述用数学归纳法证明的过程是不对的，原因是当n=k+1时，结论是利用拆项法推出来的，没有利用归纳假设n=k这一步，这不符合数学归纳法的要求．

正确的解题方法应为:当n=k+1时，有:

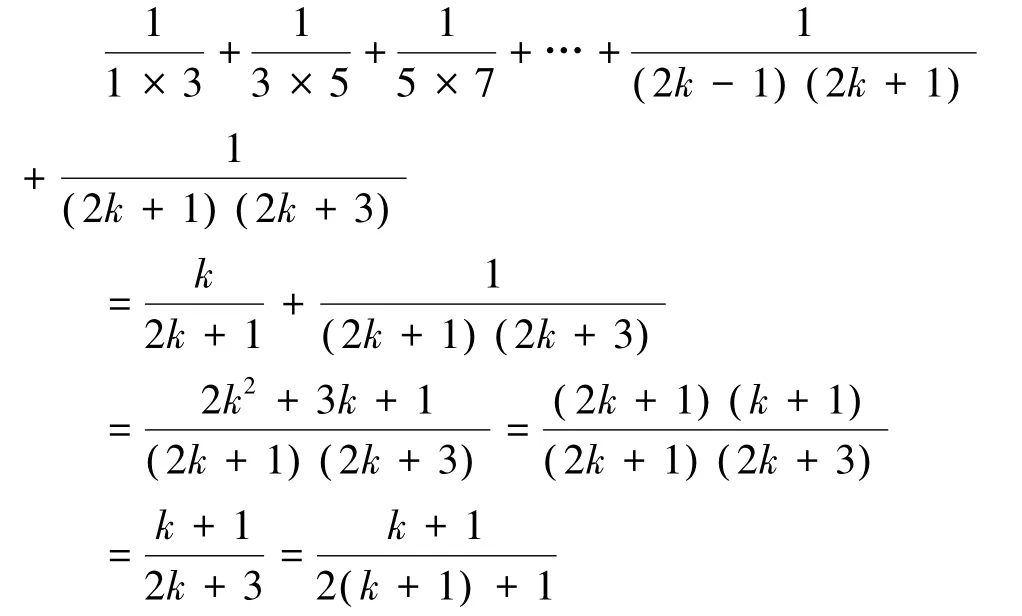
因此可知，当n=k+1时，原式也成立。

值得注意的是数学归纳法的两个步骤缺一不可。完成第二步骤时，要运用命题P(k)成立这一假定，去推导命题P(k+1)也成立。

1．3建模法

所谓建模方法，是分析和解决实际问题时，经过调查研究、了解对象信息、抽象简化后，用数学的符号和语言，把它表述为数学式子，通过计算得到模型结果来解决实际问题，并接受实际检验的方法。

例如:如果用6000元可以买一台笔记本电脑，现在先付1200元，其余部分以贷款形式按每月付900元在6个月内付清，那么，贷款的年利率为多少?

方法一:建立直观模型。把实际问题转化成数学问题，即每月还贷款800元计算，付21月的贷款利息为600元的贷款年利率多少?

由此得出期限(单位年)为21/12=7/4(年)

利息:600=800×i×7/4

i=42．86%

方法二:问题逐步分解。

(1)付款总额:1200+900×6=6600

(2)应还利息:6600－6000=600

(3)借贷金额:6000－1200=4800(P)

(4)每月还清:4800/6=800(P/n)

(5)期限:(1+2+3+4+5+6)/12=7/4(年)

(6)600=800×i×7/4，i=42．86%

1．4数形结合法

所谓数形结合就是通过“数”与“形”之间的对应、转化来解决数学问题的思想。所谓“数”，就是指数或式，所谓“形”，就是指图形或图像。在一定的条件下，它们可以互相转化，根据“数”与“形”既对立，又统一的特征，观察图形的形状，分析数与式的结构，引起联想，适时将它们相互转换，化抽象为直观并提示隐含的数量关系。

一般通过坐标系的建立，引入数量化静为动求解。或通过分析数与式的结构特点，把问题转化到另一个角度来考虑，如将转化为勾股定理或平面上两点间的距离等。或构造一个几何图形，构造一个函数，构造一个图表等。

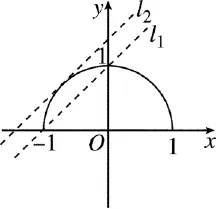
解:

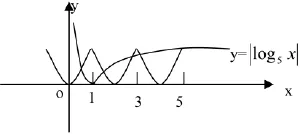
例2:已知最小正周期为2的函数y=f(x)，当x∈［－1，1］时，f(x)=x2，则函数y=f(x)(x∈R)的图象与y=|log5x|的图象交点个数为多少?

解:本题考查周期函数的图象和性质，对数函数的图象和性质及含有绝对的函数的图象的画法，本题考查数形结合思想．由图象可知，有5个交点。

例3．已知函数f(x)=|x2－4x+3|

若与y=x+a至少有三个不相等的实数根，求实数a的取值范围．

解:作出图象．

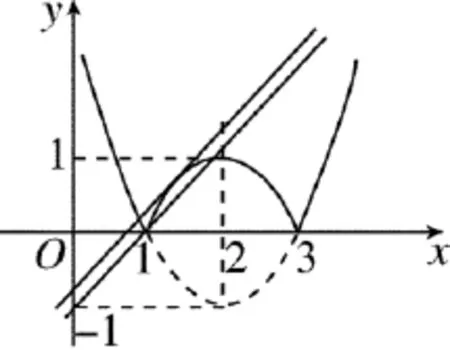
既|x2－4x+3|=x+a，于是，在同一坐标系下再作出y=x+a的图象．

当直线y=x+a过点(1，0)时，a=－1;

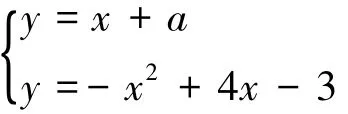
得x2－3x+a+3=0．由Δ=0．

2 结论

在教学过程中，为了很好的提高中学生问题解决的能力，应该重视学生对数学方法的掌握，重视学生应用数学方法进行解题的训练，从解题方法入手，引导数学思维，寻找解题技巧，同时，重视归纳总结，加强解题规律和方法的掌握，培养数学解题能力。

学生对数学方法的掌握，不是一朝一夕能做到的，需要教师根据教学实际，长期坚持有目的、有计划地进行培养和训练。

［1］任樟辉.数学思维论［J］.广西:广西教育出版社，1990.

［2］郑毓信，肖柏荣.数学思维与数学方法论［M］.四川:四川教育出版社，1989.

［3］涂荣豹.数学解题学习中的元认知［N］.数学教育学报，2002.

［4］钱珮玲.中学数学思想方法［M］.北京:北京师范大学出版社，2001，9.

［5］徐利志.数学方法论选讲［M］.武汉:华中科技大学出版社，2000，1.

The Analyses of the Application of Mathematical Method During the Process of Problem Solving in Middle School

ZHANG Hong－chao
(College of Mathematical Sciences，Hulunbuir College;Baotou 014030)

The article researchs the application of General mathematical method during the process of problem solving in middle school，and helps the middle school student to solve the problems through the guidance of mathematical method and form the effective strategies of solving the mathematical problems.

mathematical method;application;teaching in middle school

G632

A

1004－1869(2014)01－0095－04

2013－12－30

张鸿超(1968－):男，副教授，教育硕士，研究方向，数学教育。