在离散数学课中引入研究型题目的教学实践*

路芳

(包头师范学院数学科学学院，内蒙古包头014030)

在离散数学课中引入研究型题目的教学实践*

路芳

(包头师范学院数学科学学院，内蒙古包头014030)

为了增强学生对抽象概念的掌握和对相关知识应用的理解，将研究型题目引入离散数学教学中。通过完成阅读题目和课后实践题目，使学生提高学习兴趣，达到掌握知识、提高能力的目的。

离散数学;研究型题目;教学实践

离散数学是以离散的量及其相互关系作为主要研究对象的一门计算机专业基础课。学生通过对这门课程的学习，可以培养抽象思维和逻辑推理能力，掌握处理离散结构的描述工具和方法，提高对实际问题的数学本质的表述能力。因此，做好这门课程的教学工作，保证学生学习效果，就要将理论和实际应用结合起来，既要注重对理论进行细致的分析，又要注重实际应用的介绍和实践。通过有意识地对学生的引导，让他们感受到离散数学课程的实际应用价值。

概念多、定义抽象是离散数学课程的特点，虽然在计算机领域有着广泛的应用，但在教材中却没有很好的体现，使得学生在学习中感觉内容脱离应用，抽象难理解，影响了学习的积极性。另外，网络的高度普及应用，使得一些学习自觉性差的同学容易受到课堂外因素的吸引，影响了上课学习的主动性。

基于上述原因，教师需要通过变革教学的方式方法，不仅要想办法在课堂上吸引学生的注意力，保证课堂教学效果，而且要通过调动学生学习的积极性和主动性，使他们愿意在课堂外通过认真完成作业达到掌握知识、提高能力的目的。在教学中，我引用设计了一些研究型题目，用以改革教学模式，改进教学方法。

1 以问题的求解导入新课，激发学生学习兴趣

离散数学课程理论性强、概念抽象，要想在课堂上吸引学生的注意力，让他们跟着教师的引导一步步由理解到掌握知识，需要我们用心设计好每一节课，尤其是新课的导入环节。实践证明，通过实例问题的分析，引出相关知识的教学内容，可以增加学生的兴趣。例如在介绍逻辑推理时，可以举例:

认真听讲或者按时完成作业，是学生学习成绩好的必不可少的条件。小丽成绩好但不认真听讲。因此，小丽肯定按时完成作业。

要求学生判断以下哪项和上述的论证方式最类似。

A.一个影视作品要想有高收视率或票房价值，作品的质量和必要的包装宣传是缺一不可的。A上映以来票房价值一般但实际上质量堪称上乘。因此，它缺少必要的广告宣传。

B.必须有超常业绩或者30年以上工龄的雇员，才有资格获得公司的特殊津贴。B先生获得了特殊津贴但在公司仅供职2年，因此他一定有超常业绩。

C.如果一个公司既经营无方又铺张浪费，则一定会严重亏损。C公司虽经营无方但并没有亏损，说明它没有铺张浪费。

D.罪犯要实施犯罪，必须既有作案动机，又有作案时间，在这个案件中，D有作案动机但没有作案时间。因此，他不是该案的作案者。

E.一个论证不成立，当且仅当它的论据虚假，或者推理错误。E的论证虽然逻辑严密，推理正确，但还是被认定为不能成立。可见，她的论据有虚假的成份。

学生通过对这个问题的分析讨论，得到一个选项，但要想说明自己的选择正确与否，就需要用命题逻辑的知识来推导了。首先，将已知推理的形式结构的符号化形式写出来:

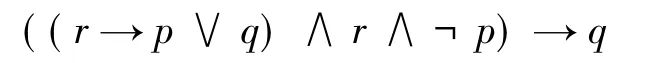
然后分别写出各选项的形式结构，通过比较得出B的推理结构与它最类似。

这样引入教学，可以抓住学生的注意力，使他们知道这节课的理论知识可以解决哪一类问题，从而明确听课的目的，保证了教学效果。

2 设置课堂教学陷阱，强调容易被忽视的问题

在课堂上，学生难免因为所学内容的枯燥而思维游离，所以在讲授知识的过程中，要用心设计一些教学陷阱，既可以集中学生的注意力，也突出了要强调的知识点。例如，在介绍有向图的关联矩阵时，先给出关联矩阵的定义:

然后给出一个带环的有向图，要求学生根据定义写出它的关联矩阵。在遇到带环的点时，矩阵中的相应元素是无法给出的，此时和学生一起分析出现这种状况的原因是这个点既是有向边的起点又是终点，无法按定义写出矩阵元素，于是对照定义强调，有向图的关联矩阵应排除带环图的情况。通过这个例子，强调了有向图关联矩阵的定义是针对没有环的有向图这一要求。经过掉入陷阱－得到解救这样的过程，强调知识的重点、难点，同时也可活跃课堂气氛、提高学生学习积极性。

3 布置课前阅读题目，了解教学内容的相关知识

离散数学是计算机学科的专业基础课，在很多后续专业课程中有广泛的应用，在学习这门课程的时候，大部分专业课还未开课，所以学生对离散数学的应用没有感受，因而影响了学习兴趣。比如，学生虽然学习过函数的内容，但在离散数学课程中，函数的概念被推广到是对离散的量的一种运算，相应的概念更加抽象了，学生学习过程中总是难以理解，感觉较中学时的内容更加枯燥无味。而这部分知识在计算机科学中非常重要，可以说，计算机对数据的输出都可以看成是输入数据的某个函数，但教材中一般都没有介绍。为了弥补这个不足，又不至占用课堂时间，可以通过布置课前阅读题目，让学生了解与课程内容相关的背景知识、前沿知识和应用实例。

例如，在计算机中存储一批数据，为了准确读取到相应的数据，要确定每个数据的位置，这样就要通过建立在存储表与数据编码间的散列(Hash)函数来进行，所以，在讲解函数前，可以出示一些例子，如:

设计算机内存中有编号从0到10的存储单元，按次序将15、558、32、102、5存入后的情形如图1所示，若要在这些存储单元中存储任意非负整数并可以进行检索。试用Hash函数完成对259和558的检索。

图1:数据与存储单元的对应关系

要求学生查找、阅读与散列函数有关的资料，了解它的定义和在计算机领域的应用。在此基础上，学生不仅可以得出本问题的解为h(259)=259 mod 11=6，h(558)=8，而且也对函数在计算机领域的应用能有一个较全面的了解，从而达到明确所学内容的实际应用，激发学习热情的目的。

4 设计课后研究型题目，锻炼解决问题的能力

关于离散数学知识的应用，并不是所有内容都适合布置课前阅读，有些知识只有在经过课堂讲授，学生对概念有了一定的理解后，才能对相关的应用有所领悟。因此，为一些知识点设计课后研究型题目，让学生在通过查阅资料，撰写学习报告来加深对新概念的理解，同时尝试用所学理论和方法去解决实际问题。

例如，在介绍了有向图的邻接矩阵后，有定理:设A为有向图D的邻接矩阵，D的顶点集为V= {v1，v2，…vn}，则A的k次幂Ak中的元素a(k)ij为D中vi到vj长度为k的通路数。这个定理教材中没有给出证明，可以布置课后作业:

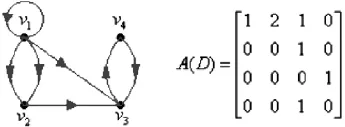
图2:有向图D及其邻接矩阵

通过对这个问题的解答，学生由定义能得到A (D)中i行j列元素表示D中vi到vj长度为1的通路数，再根据矩阵乘法的定义，分析出A2中i行j列元素表示D中vi到vj长度为2的通路数，从而在理解了定理内容实质的基础上，找到利用数学归纳法来证明本定理的方法。通过对类似问题的研究，不仅让学生接触到了所学知识的具体应用，同时也锻炼了解决问题的能力，增强了科学研究意识。

5 设置编程题目，在实践中理解和掌握算法

用计算机求解问题的基本步骤是:首先由实际问题建立起相应的数学模型，设计出相应的算法，再编程实现。离散数学知识便是在培养学生运用离散结构做出问题的抽象模型，进而构造算法的能力。所以，在每个教学模块结束时，设计一两个编程题目，要求学生解答，可以使他们在实践中掌握所学算法，提高解决问题的能力。

编程题目可以分为两类，简单的设计题目是对照数据结构中的某些算法，让学生用程序语言实现。比如编程实现对欧拉图的判定，求解最优二叉树等，通过实践对所学定义定理的应用，使抽象的理论具体化。综合性的实验题目是针对每个知识模块给出的，要求学生给出解决问题的方案，并编程实现。例如，给出一个游乐园中不同游乐项目的费用和分布情况及距离，要求学生设计出满足游客对游园线路最短、游乐项目最全等不同需求的程序。通过问题的解决，培养学生分析问题、解决问题和科学研究的能力。

通过上述几个环节的题目设计，将离散数学课的教学用各类题目串连起来。通过课前阅读了解新课程中内容的应用领域，通过问题引领完成课堂学习，再通过完成课后研究型题目加深对概念的理解，锻炼数学表达能力。这一系列的过程中，选择、设计合适的实例是实施这一教学改革的重要保证。

6 结语

引入研究型题目的教学实践，是一种通过实例增强对抽象概念的理解和对知识的应用的教学方法，达到了将理论与应用相结合的目的，有效地保证了教学质量。这种教学设计，可以提高学生学习的主动性和积极性，有利于数学建模能力的培养，对今后专业课的学习、能力的提高有很好的促进作用。

［1］马慧，等.离散数学的实例化概念教学法［J］.计算机教育，2011，(16).

［2］郭晓姝.离散数学教学模式改进探讨［J］.计算机教育，2012，(5)

［3］屈婉玲，耿素云，张立昂.离散数学［M］.北京:清华大学出版社，2008，1.

The Teaching Practice by Importing Research Problem in Discrete Mathematics

LU Fang
(Faculty of Mathematical Science，Baotou Teachers’College;Baotou 014030)

In order to strengthen students＇mastery of combine theory and application，our teaching method is Enhancing Comprehension of Concepts via research Example.By completing reading and practice to make the students understand the abstract concepts，Improve the learning interest.The goal is to achieve knowledge and improve ability of purpose.

discrete mathematics;Research Problem;Teaching practice

G642.0

A

1004－1869(2014)01－0086－03

2013－12－31

路芳(1970－)，女，山东长清人，副教授，研究方向:计算软件与理论。