图簇的伴随多项式的因式分解及其补图的色等价性*

宝音

(青海民族大学蒙学系，青海西宁810007)

宝音

(青海民族大学蒙学系，青海西宁810007)

本文利用图的伴随多项式的性质及其伴随分解的图论方法，讨论了型图的伴随多项式的因式分解，进而证明了在不同条件下这类图的补图的色等价性.

色多项式;伴随多项式;因式分解;色等价性

我们仅考虑简单图，用V(G)和E(G)分别表示G的顶点集和边集，G表示图G的补图，G1∪G2表示图G1与G2和的点不重并。NG表示N个图G的点不重并。未加说明的记号和术语均来自文［1］。设P(G，λ)是图G的色多项式，称图G与H是色等价的，若P(G，λ)=P(H，λ);称图G是色唯一的，若从P(H，λ)=P(G，λ)推出图H与G同构，记为H≌G。

1 预备知识

设G是n阶图，若图G的生成子图M的每个分支都是完全图，则称M是G的理想子图，用N(G，K)表示图G的具有k个分支的理想子图的个数，则图的色多项式可以表示为［3］，设G是n阶图，

n=|v(G)|，其中(λ)k=λ(λ－1)(λ－2)…(λ－k+1)．

定义1［3］:设G是n阶图，则多项式

称为图G的伴随多项式并且简记为h(G)。

引理1［3］:设uv∈E(G)且uv不属于G的任何三角形，则

引理2［3］:设图G有k个分支G1，G2，…GK，则h(G，x)=h(G1，x)h(G2，x)…h(GK，x)。

引理3［4］:设Pn和Cn分别表示具有n个顶点的路和圈，则有

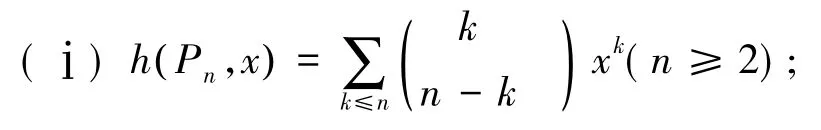
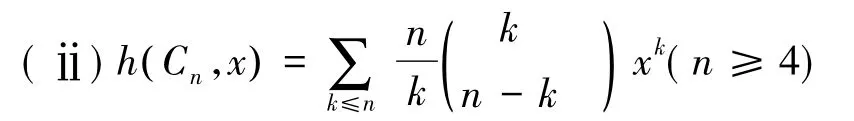
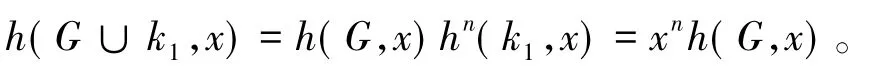
引理5［6］:(i)图G与H是伴随等价的当且仅当与式色等价的;

(ii)图G是伴随唯一的当且仅当G 色唯一的。

引理6［6］:设Sn+1是n+1阶的星图，则h(Sn+1，x)=xh(Sn，x)+xn

引理7［7］:设r，m∉N;r≥2;m≥1则

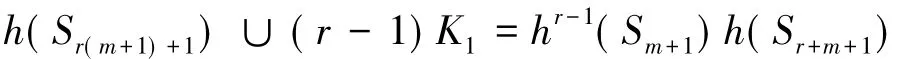
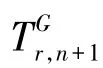
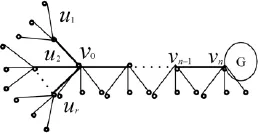
图1:图

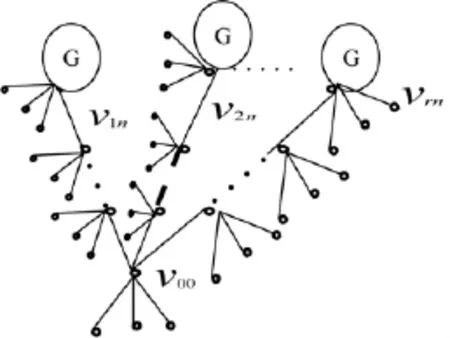
图2:图

引理8:设r≥i≥3;r≥1;n≥2则

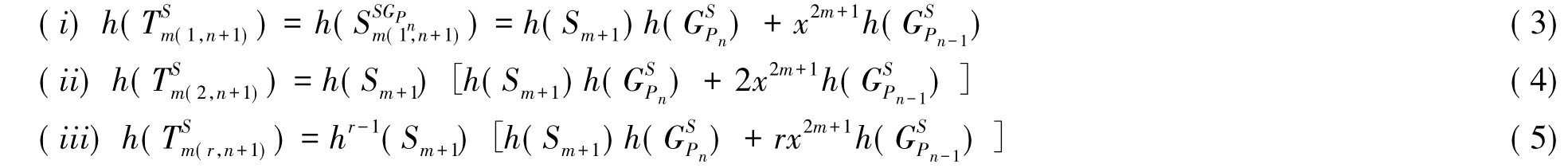
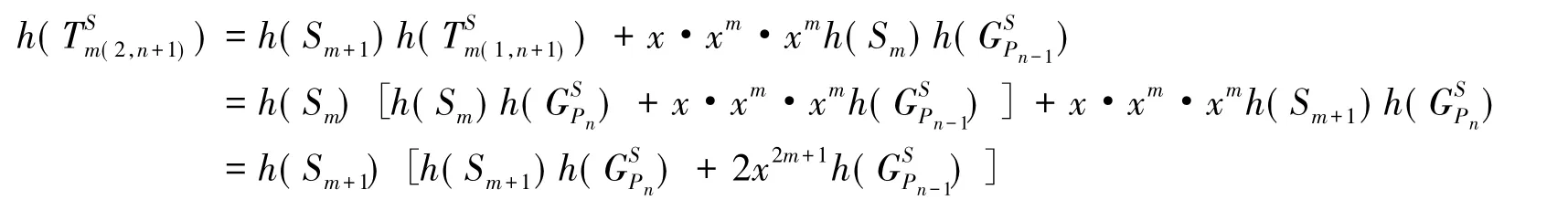
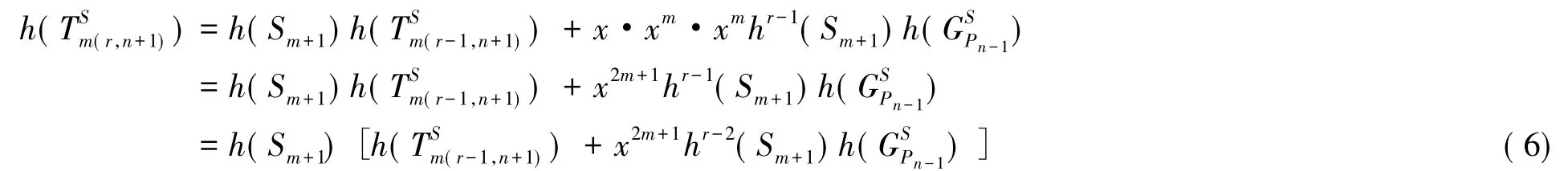
对公式(6)提出公项，逐项递推和式(ii)得

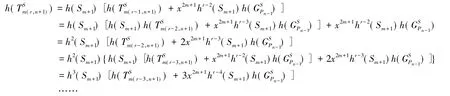
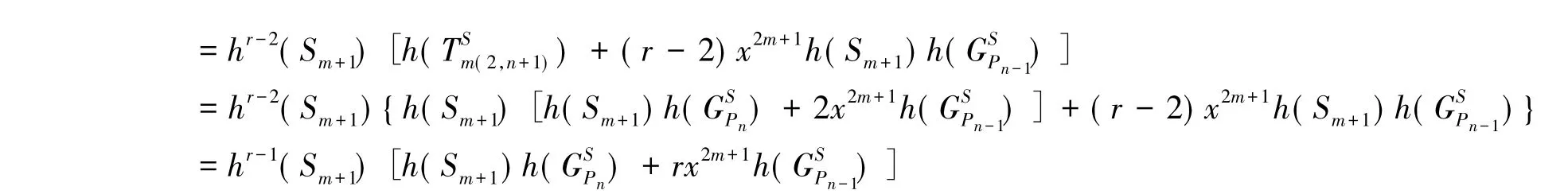
用数学归纳法来可以证明公式(5)对一切自然数都成立。

引理9:设r≥i≥3;r≥1;n≥2则

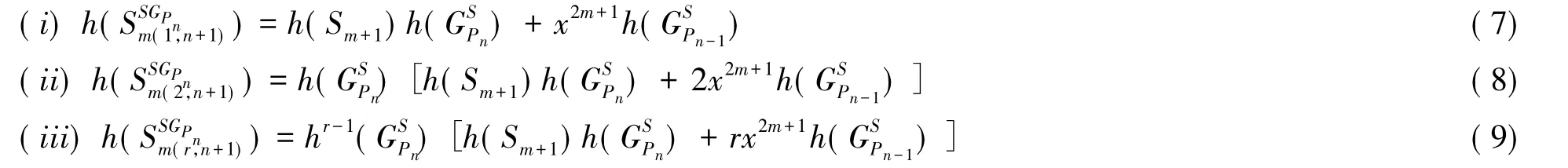
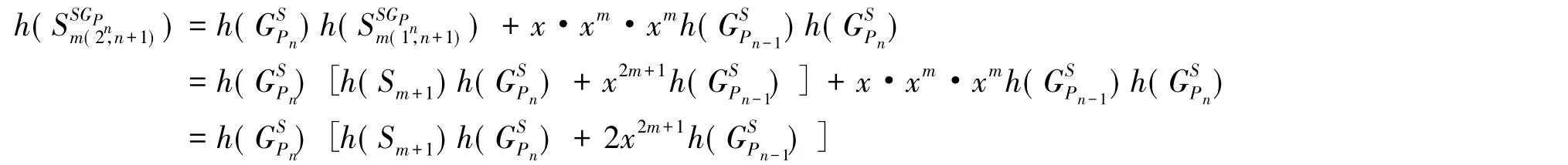
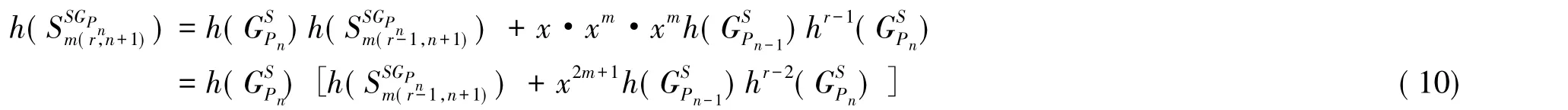
对公式(10)提出公项，逐项递推和式(ii)得

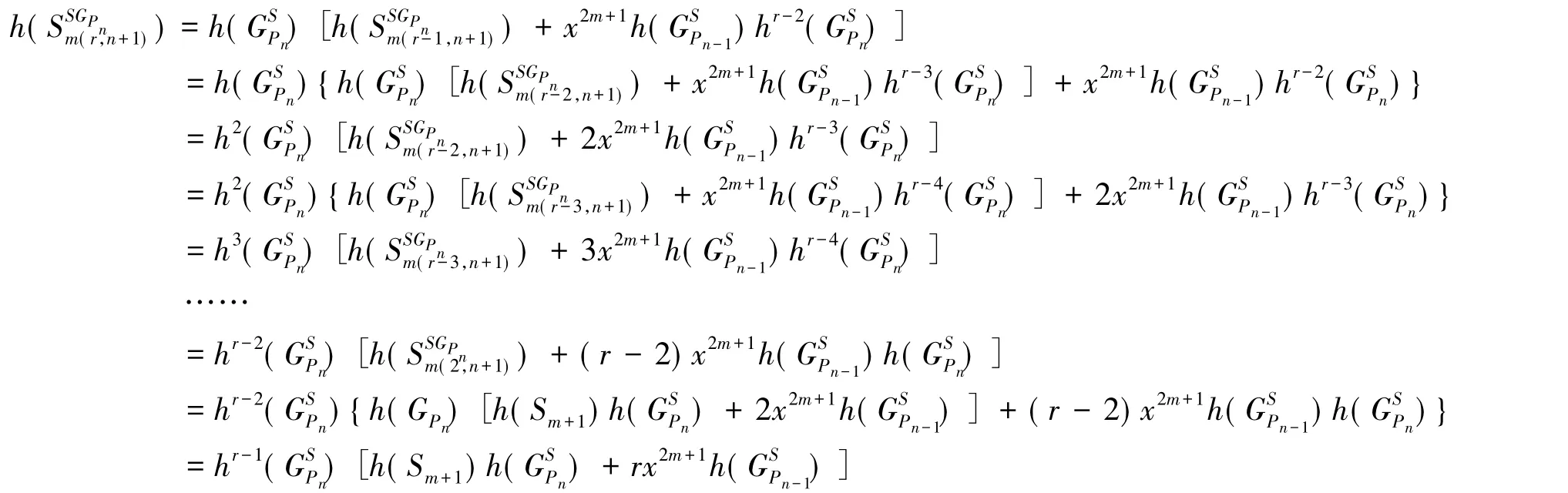
用数学归纳法来可以证明公式(9)对一切自然数都成立。

2 因式分解与色性分析

定理1:设G是不含三角形的任意p阶连通图，r≥i≥3;r≥1;n≥2则有

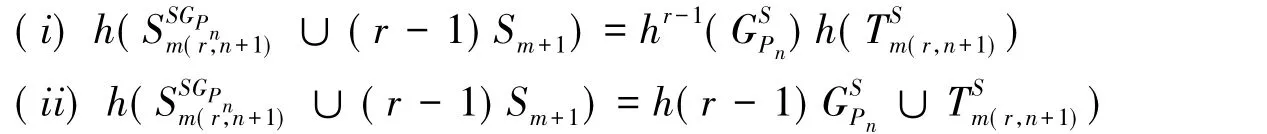
证明:由引理2，引理4，引理8(iii)和引理9(iii)，即得结论

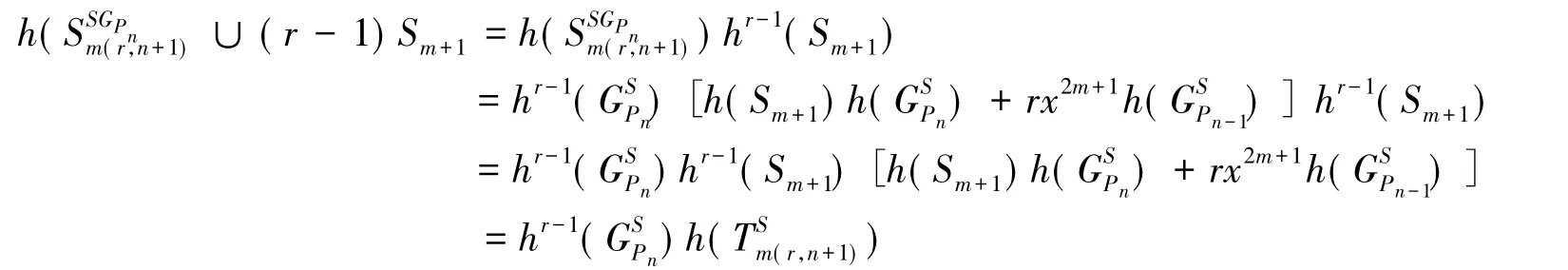
因此，即(i)的结论成立。由(i)式及引理2和引理4容易推知(ii)式也成立。

推理1:设G是不含三角形的任意p阶连通图，r≥i≥3;r≥1;n≥2则有

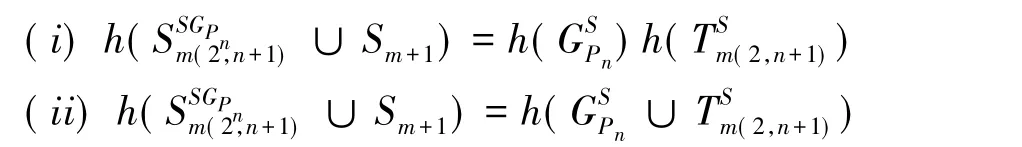
定理2:设G是不含三角形的任意p阶连通图，r，n，m∉N，r≥1;n≥2，m≥1则有

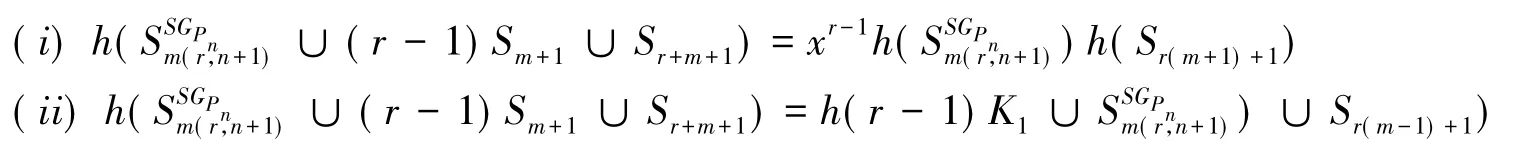
证明:由引理4，引理7和定理1，即得结论

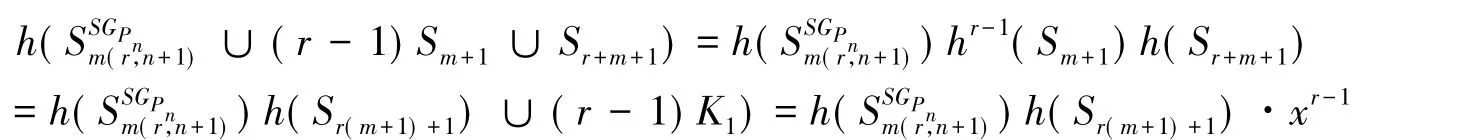
因此，即(i)的结论成立。由(i)式及引理2和引理4容易推知(ii)式也成立。

定理3:设G是不含三角形的任意p阶连通图，r，n，m∉N，r≥1;n≥2，m≥1则有

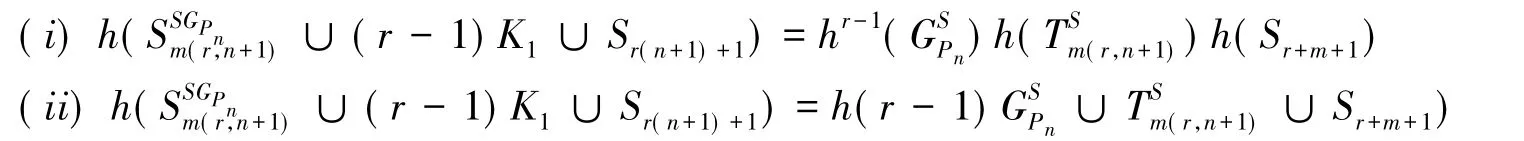
证明:由引理4，引理7和定理1，即得结论

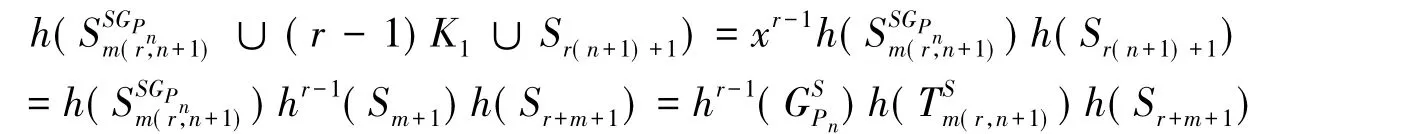
因此，即(i)的结论成立。由(i)式及引理2和引理4容易推知(ii)式也成立。

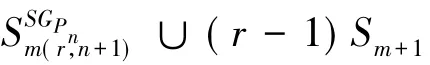
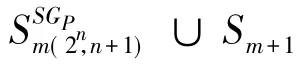
类似地，根据引理4，引理5和定理2，定理3，可证如下的结论

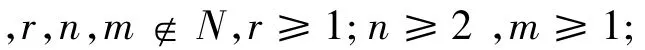
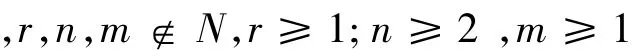
［1］Harary.Graph Theory［M］.Reading MA:Addison Wesley，1969.

［2］宝音.一类图簇的伴随多项式的恒等式及其因式分解［J］.阴山学刊，2007，21(3):9－10.

［3］刘儒英:求图的色多项式的一种新方法及应用［J］.科学通报，1987，32，77.

［4］刘儒英:关于两类图的色多项式［J］.科学通报，1987，32，236.

［5］刘儒英:Pq－1的补图的色唯一性［J］.数学研究与评论，1994，14(3):469－472.

［6］宝音，张秉儒.SP(i)类图簇的伴随多项式的因式分解及其色性分析［J］.西南师范大学学报:自然科学版，2004，29(4):573－577.

［7］曹辉.三类组合图的伴随多项式的因式分解及其色性分析［J］.西南师范大学学报:自然科学版，2007，32(5): 18－21.

The Adjoint FactorizationsofGraphs of－shape and Chromatically Equivalence of their Complement

BAO Yin
(Dept.of Mongol.，Qinghai National University;Xining 810007)

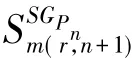
Chromatic polynomial;Adjoint polynomial;Factorization;Chromatically equivalence

O157.5

A

1004－1869(2014)01－0005－04

2013－11－04

青海省自然科学基金资助项目(2011－Z－911)

宝音(1962－)，男，内蒙古赤峰人，教授，研究方向:图论和组合数学。