关于牛顿恒等式的归纳证明
陈 聪,高稳涛,邓 勇
(1.喀什师范学院,新疆 喀什 844006;2.中国人民解放军69213部队,新疆 叶城 844900)
关于牛顿恒等式的归纳证明
陈 聪1,高稳涛2,邓 勇1
(1.喀什师范学院,新疆 喀什 844006;2.中国人民解放军69213部队,新疆 叶城 844900)
在代数学中,牛顿恒等式是联系多项式根的幂和与其系数关系的一个重要恒等式。用数学归纳法给出牛顿恒等式的一个自然证明。
牛顿恒等式;对称多项式;数学归纳法
多项式是代数学的一个基本概念,且代数式的研究都要归结为多项式性质的运用。
在代数学的多项式理论中,关于牛顿恒等式的证明已大量出现在各种文献中。例如,在文献[1]和[2]中,作者分别利用矩阵迹结论与凯莱-哈密尔顿定理和母函数与比较系数法,得到了它的两种新颖证明。除此之外,还有很多其他证明方法,在此不再赘述。本文直接利用数学归纳法给出牛顿恒等式的自然证明。
众所周知,对称多项式是多元多项式中常见的一种,其来源之一以及它应用的一个重要方面就是一元多项式根的研究,故本文从一元多项式的根与系数的关系开始。
1 预备知识
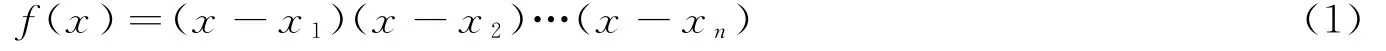
比较系数可得:
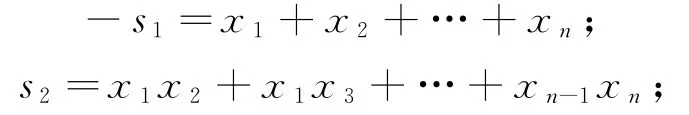
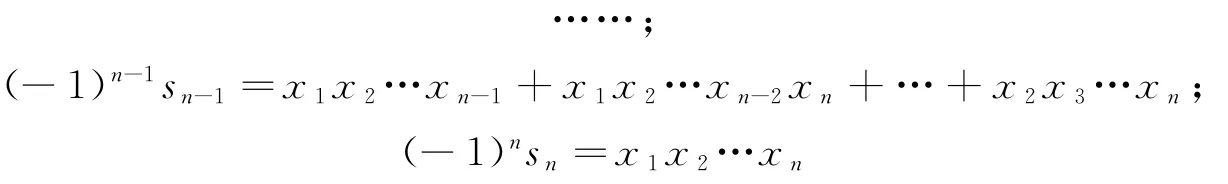
从该意义上讲,每个关于x1,x2,…,xn的对称多项式都可唯一地写成s1,s2,…,sn的多项式[3]。同时,初等对称多项式在代数学、组合数学以及数学的其他领域中也发挥着重要作用。
类似地,若设
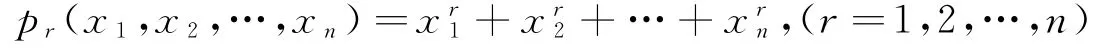
则齐次对称多项式p1,p2,…,pn也形成对称多项式(系数取自Q或R或C)空间的一组基[4]。
以上两组基s1,s2,…,sn与p1,p2,…,pn之间的变换公式被称为“牛顿公式”或“牛顿恒等式”,其最早出现在牛顿1673-1683年间所写的书《Arithmetica Universalism》中。若设那么牛顿恒等式可写成
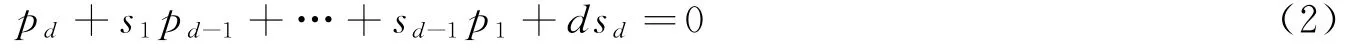
注意到,(2)式是依赖于n和d的一组恒等式。事实上,这里的n-d允许超出N的范围。
下面给出牛顿恒等式的数学归纳法证明。
2 牛顿恒等式的证明及应用举例
2.1 定理及其证明
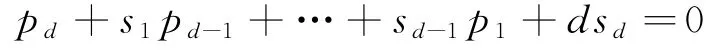
证明:对m=n-d用数学归纳法。
因m=n-d可取任何正的或负的整数值,故下面的讨论将包括m≤0的情况,即d≥n。
由s1,s2,…,sn的定义及(1)式,可得:
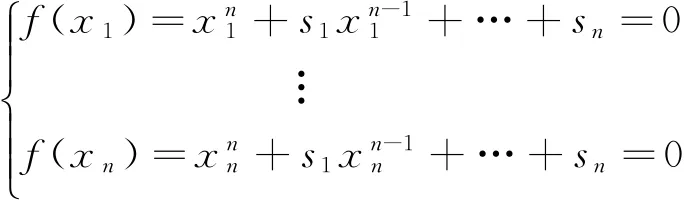
把这些方程加在一起,得到
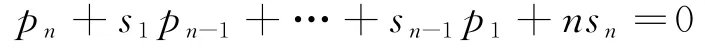
类似地,对任意的d>n,展开
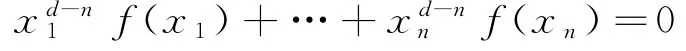
可得
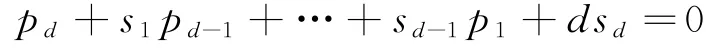
取n,d∈N,使得m=n-d≥1.假设对任何n'-d'≤m-1,都有需要证明首先,由sr和pr的定义,容易验证
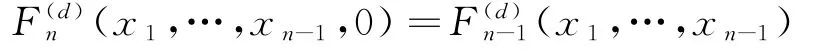
综上,牛顿恒等式成立。证毕!
2.2 应用举例
下面给出牛顿恒等式在多项式的恒等证明中的一个简单应用,以便读者可以更深刻地理解牛顿恒等式,也可参考文献[5]。
例,已知x1+x2+x3=0,求证
证 因为x1+x2+x3=0,所以,s1=p1=0,由上面定理,在中,分别令d=2,3,4,5,则可得:
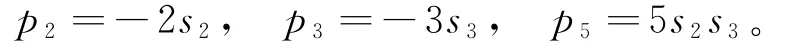
故有
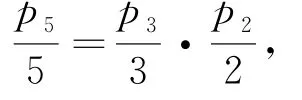
从而,
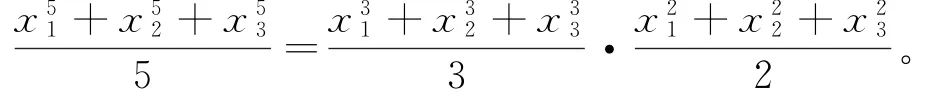
结论得证!
3 结 语
其实,在高等代数的多项式理论中,牛顿恒等式在多项式的恒等变形及其因式分解中都占有举足轻重的地位,本文用数学归纳法给出了其直接证明,并给出牛顿恒等式在证明多项式恒等方面的一个简单应用举例,这样有助于学者更深刻地理解牛顿恒等式在多项式中的应用;而在初等代数理论中,牛顿恒等式在求解方程的有关问题及实数的有关性质等等[6]问题中都有重要的应用价值,鉴于其应用如此广泛,有兴趣的读者对于其在数学其他分支领域的应用可以做进一步探究和探讨。
[1]邓勇.关于矩阵迹结论的一个应用[J].赣南师范学院学报,2008(03):28-31
[2]陈冬君,马艳芳.具有相同特征值的矩阵的刻画[J].淮北师范大学学报:自然科学版,2011(04):69-71
[3]张禾瑞,郝鈵新.高等代数[M].5版.北京:高等教育出版社,2007
[4]D G Mead.Newton’s indentities[J].American Math.Monthly,1992(8):749-751
[5]余元希,田万海,毛宏德.初等代数研究(上)[M].北京:高等教育出版社,1988
[6]周万林.牛顿恒等式的多种应用[J].数学通报,1992(02):10-12
(责任编辑:马金玉)
The Inductive Proof on Newton’s Identities
CHEN Cong1,GAO Wen-tao2,DENG Yong1
(1.Kashi Teachers’College,Kashi 844006,China; 2.The 69213rd Troop of People’s Liberation Army,Yecheng 844900,China)
Newton’s identities are an important identity that links the power of polynomial root and its coefficient in algebra.This paper shows a natural proof of Newton’s identities by using mathematical induction.
Newton’s identities;symmetric polynomial;mathematical induction
O151.1
A
1672-755X(2014)03-0011-03
2014-08-22
陈聪(1986—)女,陕西西安人,硕士,主要从事Hopf代数与量子群方面研究。
邓勇(1967—),男,新疆焉耆人,教授,硕导,主要从事矩阵及其数值计算等方面研究。

