基于MUSIC算法的天线系数测量信号分析方法

刘星汛，张 涛

基于MUSIC算法的天线系数测量信号分析方法

刘星汛1,2，张 涛1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 北京无线电计量测试研究所，北京 100058)

基于自由空间场地衰减数学模型，提出多重信号分类(MUSIC)算法的信号分析方法，从在固定天线高度测量的场地衰减信号中，提取直射波场地衰减量，推算远场天线系数．取谐振频率为500,MHz的半波偶极子天线为研究对象，在300,MHz～1,GHz频率范围内进行实验验证．结果表明，此分析方法提取的直射波场地衰减与采用矩量法的仿真值吻合较好，利用此场地衰减推算的远场天线系数与CISPR16-1-6的标准场地法测量的天线系数一致性较好，此算法可以用于天线系数测量的信号提取．

天线系数；MUSIC算法；天线；信号处理

在电磁兼容(electromagnetic compatibility，EMC)辐射发射试验中，常常用天线作为辐射接收设备．天线系数是EMC天线最重要的参数，天线测量位置的辐射场强E=U+Fa(其中U为测量信号耦合在天线端口处所产生的电压，Fa为测量天线的天线系数)，待测信号辐射场强测量值与所用天线的天线系数直接相关，天线系数测量的准确性直接影响到辐射测试的结果．因此天线在使用之前需对其天线系数进行测量．

天线远场天线系数校准常常采用标准场地法，标准[1-2]规定了天线系数校准所使用的场地要求和测试方法，频率30,MHz～1,GHz以下的发射天线架高2,m，接收天线1～4,m扫描．此种方法能准确地测量出天线的远场天线系数，但是在每个频率点，接收天线都要扫描多次才能找出测量的最大场强，耗时多，效率低．

Bennett等[3]和McConnell[4]提出发射、接收天线在固定高度上测量天线系数的方法，虽然耗时小，但是存在场地的微小差异而造成场强测量值的巨大偏差等问题．Smith等[5]提出标准场地法是基于FCC场地衰减理论，地面反射波对Friis自由空间方程平均影响在4.7,dB，采用接收天线1～4,m扫描测量最大场强可以避免场强测量偏差大的问题，其问题的本质是地面差异影响了地面反射波的特性参数从而导致接收天线处接收的直射波与地面反射波场强叠加的差异．

笔者基于多重信号分类(MUSIC)算法[6]，通过将信号的协方差矩阵进行奇异值分解，将信号与噪声分开，构造信号空间谱函数，通过功率谱峰值搜索，可以判断信元的一维距离像，将此信号分析方法用于天线系数的校准，可以区分噪声、直射波和反射波所引起的场地衰减，从而在固定天线高度条件下，实现天线系数的准确测量．

1 基于空间平滑处理(SSP)的MUSIC算法

1.1 基于SSP处理的MUSIC算法

MUSIC算法[6]是一种基于矩阵特征空间分解的方法，将所观测的信号空间分解成信号子空间和噪声子空间．具体有4个步骤.

步骤1 求测量信号的相关矩阵ˆR．

假设接收天线测量的场地衰减信号A在某采样频率点fi(i=1，2，…，n，n为数据点数)处的值为yi，则yi包含了直射波信号AFS,i、地面反射波信号ARF,i和障碍物散射信号ASC,i以及其他噪声信号ci，则电磁波到达接收天线的传输方程为

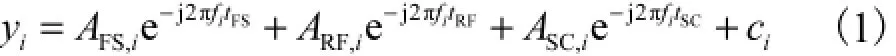
式中：tFS为直射波到达接收天线的传输时间；tRF为地面反射波的传输时间；tSC为障碍物散射波的传输时间．

将测量频率范围分成若干个窄带，在每个窄带范围内，由于各采样点频率接近，场地衰减信号可视为常数，每个窄带范围内均匀采样L次共得到L个数据样本，将采样数据样本分成M个子阵列，每个子阵列含有N个采样点，L=N+M-1，如图1所示，子阵列中的测量信号矩阵Y由N个y组成，可以表示为

可以简化矩阵的形式为

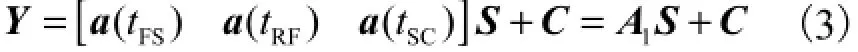
式中：Y为N×1维数据矢量，由N个y组成；A1为N×3维信号传输时间矩阵；S为3×1维空间信号矢量；C为N×1维噪声数据矢量．

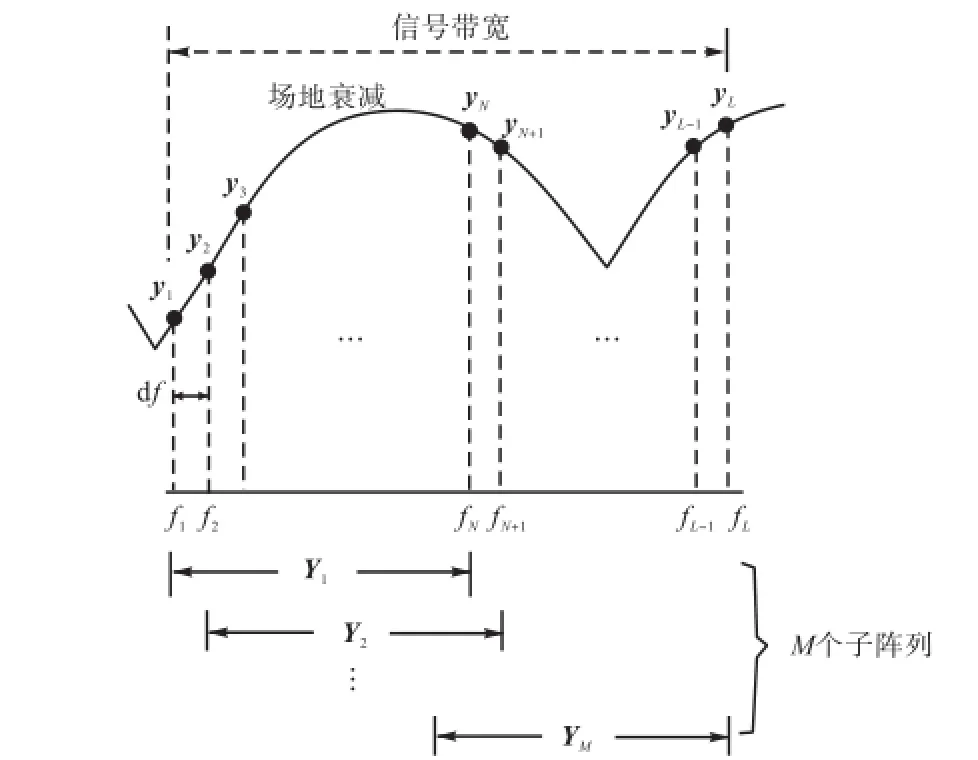
图1 测量信号采样方法Fig.1 Sampling method for measurement signal

假设在频带范围内，共进行L次采样观测，得到L个观测数据样本，数据矢量矩阵的相关矩阵为式中：ˆkR为第k个子阵列的数据矢量矩阵的相关矩阵，其中k为1～M的任意值；yk(i)为第k个子阵列中的第i个数据矢量(i=1，2，…，n)；H为共轭转置.

步骤2 数据矢量SSP前处理．

由于MUSIC算法不能很好地分辨相关信号，因此采用SSP算法[7]对数据矢量进行去相关处理．

式中Rˆssp为SSP前处理后的数据相关矩阵．

步骤3 对Rˆssp进行特征值分解，确定信号子空间UˆS和噪声子空间UˆN，根据功率谱函数进行峰值搜索，对自相关函数Rˆssp进行特征值分解，其中特征值为(λ1，λ2，…，λm)，对应的特征向量为(e1，e2，…，em)，根据MUSIC算法特性[6]，噪声子空间由相关矩阵Rˆssp中所有最小特征值(噪声方差)对应的特征向量UˆN组成，它与信号子空间矩阵A1正交，根据功率谱函数进行峰值搜索，其中峰值极大点所对应的时间，即是各信号到达接收天线的传输时间

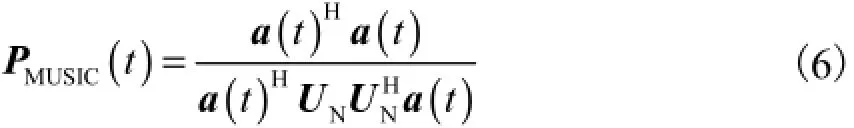
步骤4 计算自由空间场地衰减AFS．AFS、ARF、ASC的计算式[8]为

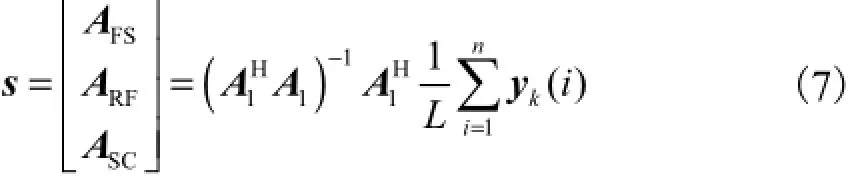
1.2 算法实现

整个算法是在Matlab6.5中实现的，MUSIC算法数据处理流程如图2所示.

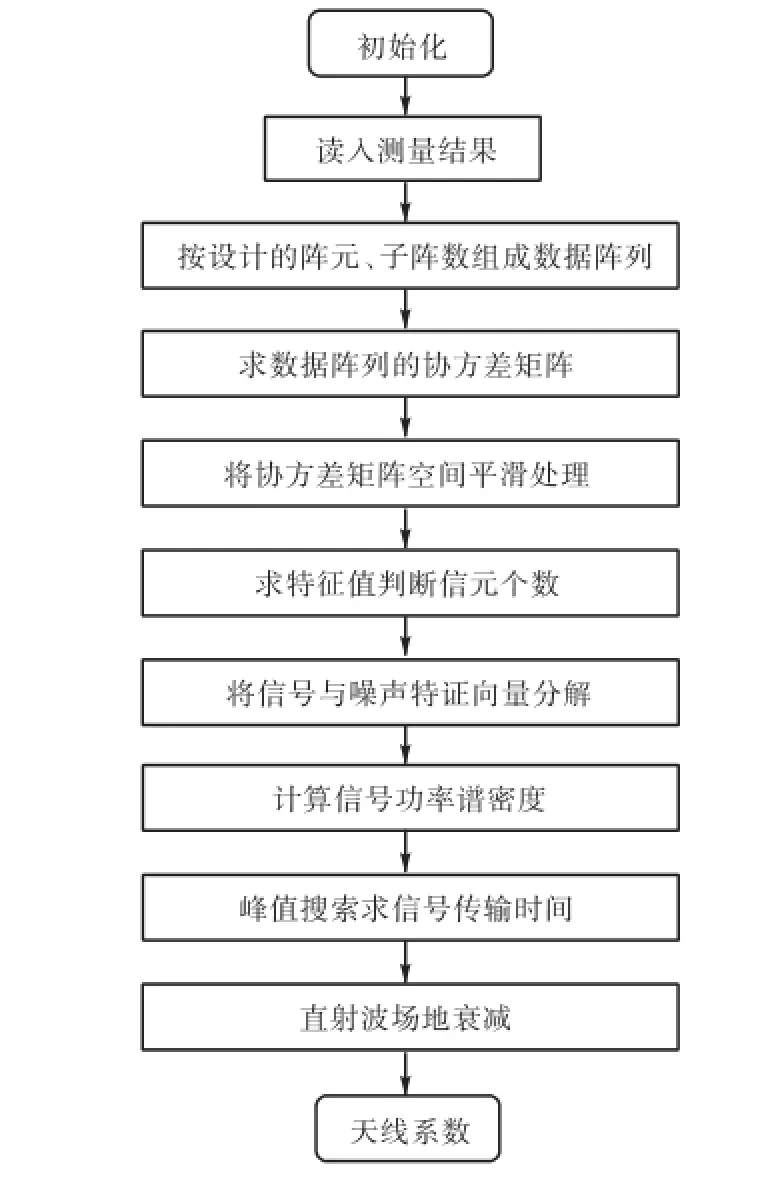
图2 信号处理流程Fig.2 Flow chart of signal processing

2 实验验证及结果分析

为了验证算法的有效性，选用场强可精确计算，谐振频率为500,MHz的一对半波偶极子天线(HZ-12、HZ-13)作为研究对象，由于300,MHz以下，偶极子接收的信号幅值太小，因此选择频率测量范围为300,MHz～1,GHz．采用矢量网络分析仪(AV3629D)作为信号发生和接收设备．

2.1 偶极子天线系数测量方法

如图3所示，天线系数测量在半电波暗室中进行，发射天线与接收天线垂直极化，且架高h，相距d(此处取h=4,m，d=3,m)，接收天线收到2路电磁波信号，一路是发射天线发出的电磁波直接被接收天线接收，另一路是发射天线发出的电磁波经地面反射进入接收天线[9]．2路信号进入接收天线的时间差为

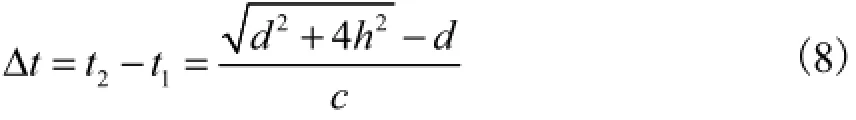
式中：d为天线之间的距离；h为天线架设的高度；c为光的传播速度．

假设接收天线测量的场地衰减信号为A，直射波对场地衰减贡献为AFS、地面反射波对场地衰减贡献为ARF，根据直射波与发射波的传输时间差，将测量的场地衰减信号A通过MUSIC算法提取自由空间场地衰减AFS．

根据CISPR 16-1-6[1]，自由空间场地衰减数学模型(无地面反射波和任何反射物)为

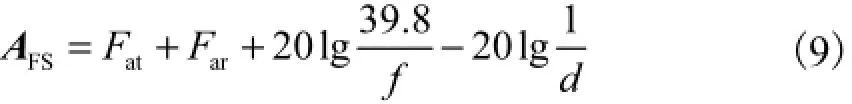
式中f为频率，MHz．

当发射天线与接收天线相同时，Fat=Far，则天线系数为

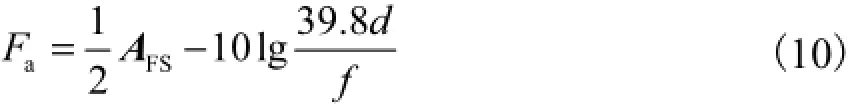
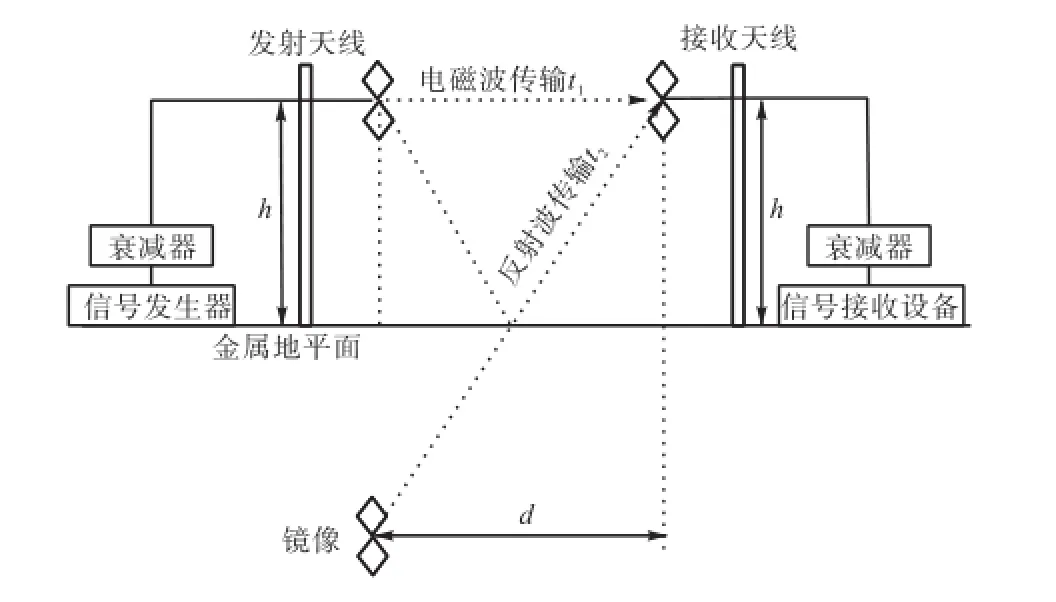
图3 天线系数测量示意Fig.3 Antenna factor measurement layout

2.2 实验结果及分析

按照以上描述的布置条件，测量偶极子天线的场地衰减，结果如图4所示，将测量的场地衰减A进行SSP前处理MUSIC算法信号分析，取子阵阵元个数为10，频率步进5,MHz，信号带宽BW分别取20,MHz、30,MHz、50,MHz，其功率谱峰值搜索结果如图5所示，带宽越大，搜索效果越好，然而在程序中，单个带宽频率范围内，认为场地衰减相同，而实际上不同频率场地衰减不同，因此加大带宽同时会使引入的误差变大．图5中当带宽较窄(取20,MHz)时，功率谱只有1个峰值，这是因为信号域搜索区模糊，不能搜索到所有信源，当带宽加大到30,MHz、50,MHz时，功率谱出现2个峰值，可清晰地分辨出直射波和反射波2路信号，2个峰值对应的时间差为21,ns，与理论值18.5,ns吻合较好．

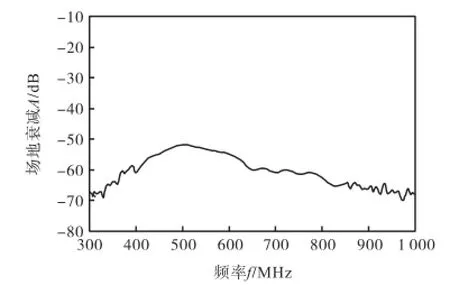
图4 偶极子天线场地衰减A测量值Fig.4 A measurement values of dipole antenna

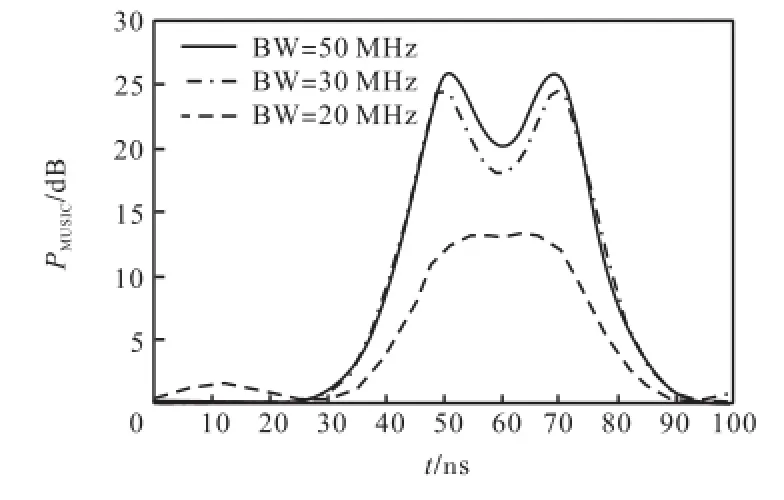
图5 MUSIC算法信号处理后功率谱Fig.5 Power spectra after MUSIC algorithm signal processing

图6 为MUSIC处理后的自由空间天线系数Fa处理值和半波偶极子天线AFS仿真值比较；图7为两者之间的差值．仿真不考虑阻抗匹配、线缆损耗、环境噪声等实际情况所引入的不确定度，采用矩量法模拟两个相同的半波偶极子天线在架设4,m高度、之间相隔距离3,m条件下的自由空间场地衰减值[10]．从图6和图7可知，MUSIC信号处理后的场地衰减AFS与理论仿真值吻合较好，整个频段内，场地衰减相差均在±1,dB以内，在1,GHz频率点上，场地衰减误差最大为-0.8,dB，是因为偶极子天线在1,GHz已经到达工作频率限值，接收的信号幅值小，信噪比相对较小，所以使误差变大．

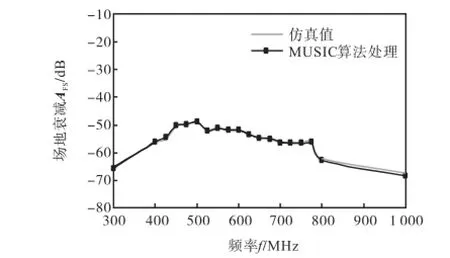
图6 AFS的MUSIC算法信号处理值和仿真值Fig.6 AFSdata of simulator and processing data with MU-SIC algorithm

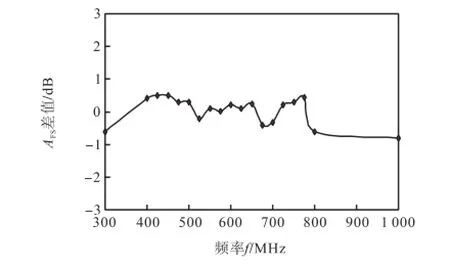
图7 MUSIC算法处理值与仿真值的差值Fig.7Difference between processing data withMUSIC algorithm and simulator

图8 为偶极子天线的天线系数；2条曲线分别为MUSIC算法信号处理后所得的自由空间天线系数AFS(代入式(10)的计算结果)和采用标准场地法[1-2]SSM测量的天线系数校准结果．从图8可知，除了频率点300,MHz、1,GHz两点以外，采用信号处理方法所计算的天线系数与标准场地法天线系数校准值相差在0.5,dB以内，充分证明基于MUSIC算法的信号分析方法能够有效地将不同信源区分，实现了频率低于1,GHz以下的电磁兼容天线的远场天线系数在固定架设高度下的准确测量，避免了标准场地法测量过程中1～4,m天线扫描，可缩短天线计量时间，提高天线计量效率．

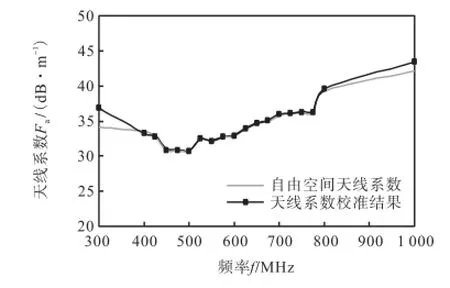
图8 偶极子天线系数的信号处理值与校准值Fig.8Signal processing values and calibration valuesof dipole antenna factor

3 结 语

本文研究了一种基于MUSIC算法的EMC测试天线的天线系数测量信号分析方法，通过信号传输时间差，将直射波与反射波信号区分，实现了直射波信号场地衰减分量的提取．实验结果表明，天线架设在固定高度，通过此信号分析方法能有效地计算出天线的远场天线系数．

根据此信号分析方法的去噪原理，分析天线校准场地环境不理想对测量信号产生的噪声特点，将可用于天线系数现场校准结果的修正．

［1］ Draft CISPR 16-1-6 EMC Antenna Calibration[S]. FDIS，2012.

［2］ ANSIC 63. 5—2006 American National Standard for Electromagnetic Compatibility-Radiated Emission Measurement in Electromagnetic Interference(EMI)Control-Calibration of Antennas(9,kHz to 40,GHz)[S]. New York，USA，2006.

［3］ Bennett W S，Taggart H E. Characterization of a farfield EMI test site with ground screen[C]// The 3rd Symposium Technical Exhibit. Rotterdam，the Netherlands，1979：507-513.

［4］ McConnell R A. A method of determining free space antenna factor on an open area test site[C]// Proceedings of IEEE International Symposium on Electromagnetic Compatibility. Washington，DC，USA，2000，2：499-504.

［5］ Smith A A，German R F，Pate J B. Calculation of site attenuation from antenna factors[J]. IEEE Trans on EMC，1982，24(3)：301-315.

［6］ Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans on Antennas Propag，1986，34(3)：276-280.

［7］ Chen Yimin. On spatial smoothing for two-dimensional direction of arrival estimation of coherent signals[J]. IEEE Trans on Signal Processing，1997，45(7)：274-278.

［8］ Yamada H，Ohmiya M，Ogawa Y，et al. Super resolution techniques for time-domain measurements with a network analyzer[J]. IEEE Trans on Antennas Propag，1991，39(2)：177-183.

［9］ Zhang Wei，Xi Xiaoli. Analysis and simulation of the direction of arrival estimation algorithm of spatial signal [C]// The 8th International Conference on EMI. Xi’an，China，2007：576-579.

［10］ Jungkuy P，Dongchan J，Hoon Y，et al. Mutual comparison on calibration of free-space antenna factor for EMI antenna in 30,MHz—1,GHz[C] // The 19th Asia-Pac Symp EMC. Singapore，2008：875-878.

(责任编辑：孙立华)

MUSIC Algorithm-Based Signal Analysis Method of Antenna Factor Measurement

Liu Xingxun1,2，Zhang Tao1
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Beijing Institute of Radio Metrology and Measurement，Beijing 100058，China)

A signal analysis method based on multiple signal classification(MUSIC)is proposed for distilling the site attenuation(SA)of direct wave from SA measurement with antenna at fixed height. Based on free-space site attennation mathematic model，the far field antenna factor was calculated using the direct wave SA. A half-wave dipole antenna with tune frequency 500,MHz was used in experimental measurement in the frequency range of 300,MHz～1,GHz. The direct wave SA agreed well with simulation with the method of moments(MoMs). The far field antenna factor calculated was well consistent with the value measured using standard site method(SSM)of CISPR 16-1-6. Therefore the antenna factor measurement signal can be extracted by the signal analysis method based on MUSIC efficiently.

antenna factor；MUSIC algorithm；antenna；signal processing

TG156

A

0493-2137(2014)10-0909-05

10.11784/tdxbz201308011

2013-08-05；

2014-01-05.

国防科工局资助项目.

刘星汛（1982— ），女，博士.

刘星汛，xun_zi_jing@163.com.

时间：2014-03-25.

http：//www.cnki.net/kcms/doi/10.784/tdxbz201308011.html.