一种1T2R并联动力头的运动学分析与优化设计

宋轶民，张嘉滕，孙 涛

一种1T2R并联动力头的运动学分析与优化设计

宋轶民，张嘉滕，孙 涛

(天津大学机构理论与装备设计教育部重点实验室，天津 300072)

面向飞机等大型结构件高效加工的需求，提出了一种新型5坐标可重构作业单元执行机构(称之为1T2R并联动力头)的运动学分析与设计方法．首先，借助闭环矢量法构造该类3自由度并联动力头的位置逆解模型，推导量纲统一的速度雅可比矩阵．利用数值搜索法搜索该机构的可达空间，研究关键参数对工作空间的影响规律．然后，以动平台外接圆半径为参照归一化设计参数，利用量纲统一雅可比矩阵的条件数构造兼顾机构运动学性能平均水平与波动量的全域评价指标，将其作为目标函数．最后，依据工程需求及性能要求，结合工作空间分析，确定约束条件，利用灵敏度分析实现机构尺度参数的综合，并用MATLAB遗传算法工具箱予以验证．此研究成果可为该类1T2R并联动力头的详细机械设计奠定理论基础．

并联动力头；运动学；量纲统一的雅可比矩阵；尺度综合

在航空制造领域，为了在减轻质量的同时保证设计强度，现代飞机、火箭等飞行器设计广泛采用整体结构件．整体结构件的材料去除率约占成品件的80%以上，因此，整体结构件数控加工装备在航空制造业中至关重要．

目前，整体结构件数控加工装备的解决方案大体有两种，一种是基于串联构型的大型5坐标龙门式数控装备，该类装备结构简单，但是体积和质量大、可重构能力差，难以满足大型结构件高效加工的需求；另一种是基于并联构型的数控装备，该类装备具有可重构能力强、精度高、刚度大等优点，基于Tricept机构[1]和Sprint Z3动力头[2]的串并混联5坐标加工中心便是它们的典型代表．由于技术壁垒及军事、政治等影响因素，串并混联的大型结构件高效数控加工装备必须依靠自主研发．

以Sprint Z3为代表的并联动力头，具有一平两转3个自由度，末端无需串接转头便可在安装电主轴后直接用于加工作业，使得该类机构末端质量更轻，动态特性更好，受到工业界和学术界的广泛关注．从拓扑构型上看，这类机构大致可分为两类，一类是全部由欠约束支链组成，另一类是由无约束支链和恰约束支链组成．Sprint Z3便属于前者，相关的研究成果[3-4]较多，而对于后者的研究相对匮乏．本文研究的机构属于后者，由静平台、动平台、3条无约束主动UP S支链及1条恰约束从动PU支链构成(U、P、S分别表示虎克铰链、移动副和球铰链，P,表示主动移动副)，称之为3-UP S&PU并联动力头[5]．同Sprint Z3动力头类似，该动力头也属于绕A、B轴摆动类型，而该类型的动力头相比绕A、C轴摆动的动力头更能满足高效加工的需求．由于其从动支链的移动副与静平台直接相连，使得该动力头在卧式布局的时候具有重力自平衡的优点．以3-UP S&PU并联动力头为核心功能部件，并与x、y轴串联集成，可搭建一种新型5坐标可重构高效混联作业单元．

需要指出的是，鲜有文献系统地对3-UP S&PU这类1T2R 3自由度并联动力头进行运动学分析和设计．因此，本文以3-UPS&PU并联动力头为对象，对其运动学分析和优化设计开展研究．在用闭环矢量链法[6]建立其运动学模型的基础上，推导得到量纲统一的雅可比矩阵．采用数值方法搜索机构的可达空间，分析尺度参数对其工作空间体积的影响，得到几何与运动约束条件．进而利用雅可比矩阵的条件数构造兼顾机构运动学性能全域平均水平与波动量的目标函数[7-10]，实现对该机构的优化设计，以期为此类大型结构件5坐标混联高效数控加工中心的进一步研究奠定理论基础．

1 机构描述

5坐标混联作业单元见图1(a)；如图1(b)所示，3-UP S&PU并联动力头的3条UPS支链呈轴对称分布，UPS支链一端通过虎克铰与静平台连接，另一端通过球铰与动平台相连．PU支链一端通过虎克铰与动平台连接，另一端为移动副与静平台相连．

图1 3-UPS&PU并联动力头虚拟样机Fig.1 Virtual prototype of 3-UPS&PU parallel manipulator

3-UPS&PU并联动力头的结构简图如图2所示，其中，点Bi(i=1，2，3)表示第i条UPS支链的连架虎克铰中心，点Ai表示该支链与动平台相连球铰的中心；点A4表示PU支链连接动平台的虎克铰的中心，即该支链虎克铰内外圈支承轴线的交点．定义由点Bi组成的平面为静平台平面，由点Ai组成的平面为动平台平面．不失一般性，由点Bi所构成的三角形△B1B2B3为等边三角形，该三角形的中心为O，其外接圆半径为b．同样，由点Ai构成的三角形△A1A2A3也为等边三角形，该三角形的中心为P，其外接圆半径为a．PU支链移动副轴线与静平台平面正交，且交点恰为点O．从点A4向动平台平面所做垂线的垂足恰为点P．点----→C为动平台末端参考点；q4为PU支链的长度(即OA4的模)；d为A4P线段的长度．

为描述动力头的运动，以点O为原点建立固定坐标系Oxyz，其中y轴与线段B1B2平行，z轴与静平台平面垂直，x轴满足右手定则．以点A4为原点建立动坐标系A4uvw，其中u轴与PU支链虎克铰内圈支承轴线重合(该虎克铰的外圈支承轴线与y轴平行)，w轴垂直于动平台平面并朝下，v轴满足右手定则.同时，为描述各UP S支链在固定坐标系下的位姿，建立支链固定坐标系Bixiyizi和支链连体坐标系Biuiviwi(i=1，2，3)，其中xi轴与UP S支链连架虎克铰近架轴线重合，zi轴与z轴平行，yi轴满足右手定则，vi与该支链i的连架虎克铰远架轴线重合，wi沿支链轴线方向从点Bi指向点Ai，ui轴满足右手定则．第i条UP S支链首先绕xi轴旋转φui角，再绕旋转之后的vi轴旋转θui角达到其当前的姿态．

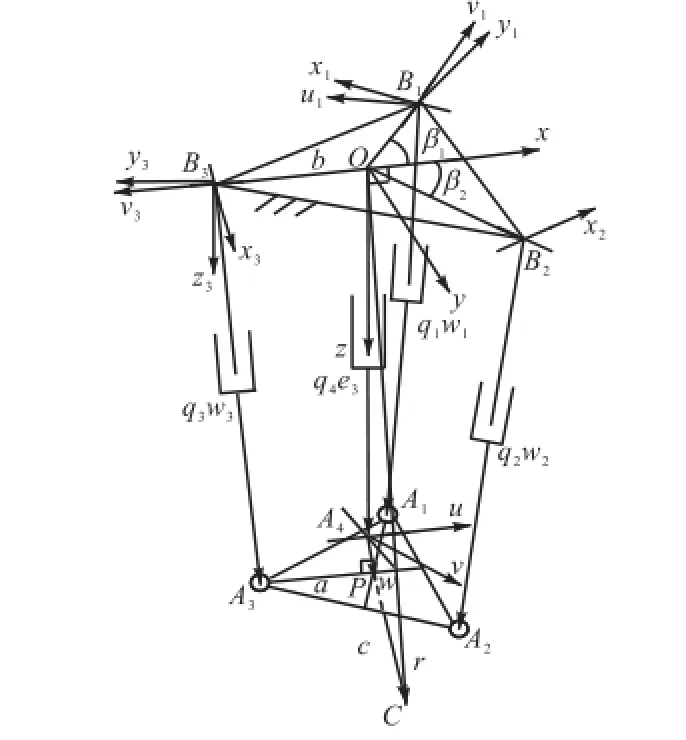
图2 3-UPS&PU并联动力头结构简图Fig.2 Schematic diagram of the 3-UPS&PU parallel manipulator

根据上述定义，坐标系A4uvw相对坐标系Oxyz的姿态可通过首先绕y轴旋转β角，然后绕旋转后的u轴旋转α角实现．据此，坐标系A4uvw相对坐标系Oxyz的姿态矩阵为

式中u、v和w分别表示轴u、v和w在固定坐标系下的单位矢量．若已求得w =()T，则可得PU支链姿态角

2 位置逆解模型

并联机构的位置逆解是指已知动平台末端参考点的位矢，求解各驱动支链的输入．设动平台末端参考点C到动平台中心P的距离为c．若已知参考点C在坐标系Oxyz中的位置矢量为r=(xCyCzC)T，则PU支链的长度q4为

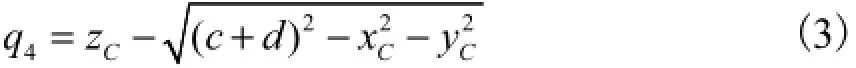
同时，在坐标系Oxyz下构造位置闭环矢量约束方程

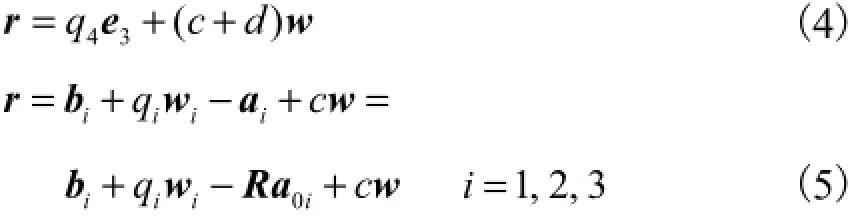
式中：e3为沿z轴正向的单位矢量；qi、wi分别为UP S支链的杆长和wi轴的正向单位矢量．ai、bi分别为PAi、OBi．以上各矢量均在固定坐标系下度量. a0i为PAi在坐标系A4uvw下的矢量，且a0i=，其中βi=(2i-3)π/3．由式(4)可以求出w，进而由式(2)和式(1)求出姿态变换矩阵R．又由wiTwi=1，得

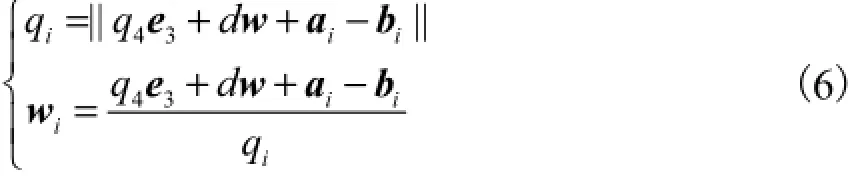
3 雅可比矩阵

本节将借助闭环矢量法推导3-UPS&PU并联动力头的6阶完整速度雅可比矩阵以及3阶量纲统一的雅可比矩阵．

式(5)两端关于时间求导，得

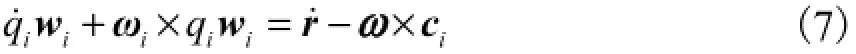
式中：r˙为动平台末端参考点C的线速度；ω为动平台的角速度；q˙i为第i条支链沿轴线的速率；ωi为第i条支链的角速度；ci为AiC在固定坐标系下的矢量，ci=-ai+c w．

式(7)两端分别用wi做点积，得

将式(8)整理成矩阵形式，可得

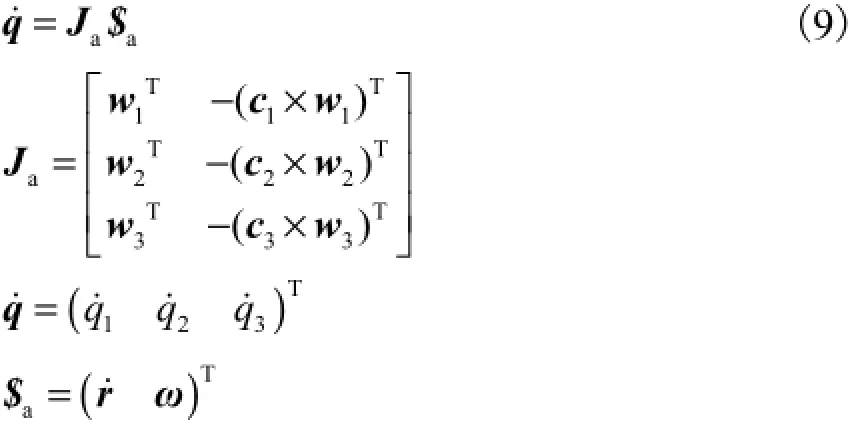
式中Ja为3-UPS&PU并联动力头的驱动雅可比矩阵.

针对从动支链为恰约束支链的特点，推导约束雅可比矩阵．式(4)两端关于时间求导，得

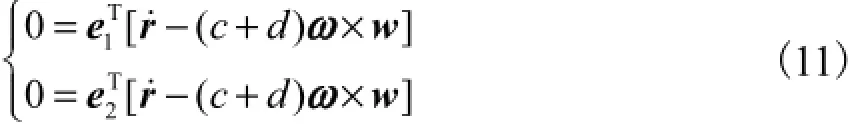
式中1e、2e分别为x轴和y轴的单位矢量．此外，注意到动平台的角速度满足以下约束方程

式中n为PU支链虎克铰两轴线所在平面的法线，n=e2×u．

将式(11)和式(12)整理成矩阵形式可得

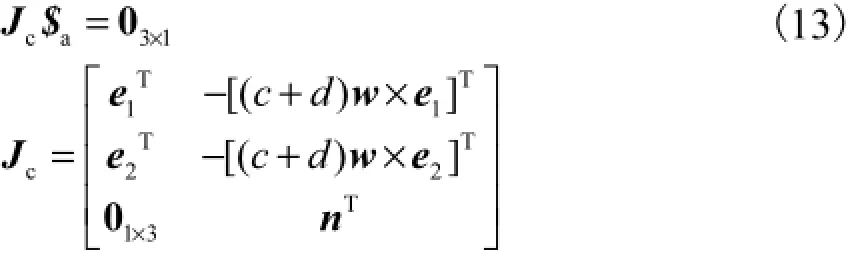
式中cJ为并联动力头的约束雅可比矩阵．由式(9)和式(13)得

式中：q˙0=(q˙1q˙2q˙3000)T；Jx为3-UPS &PU并联动力头的完整雅可比矩阵，表示为

因3-UPS&PU并联动力头为平转耦合的姿态机构，其雅可比矩阵中含有线、角速度量纲不统一的问题，若基于此矩阵构造性能评价指标，会导致机构性能评价和尺度综合过程中物理意义不明确．故本文将动平台角速度用点C的线速度表示，得到量纲统一的雅可比矩阵，并据此构建性能评价指标，完成后续分析和设计．

基于式(13)，动平台的角速度可由其末端参考点C的线速度表示为

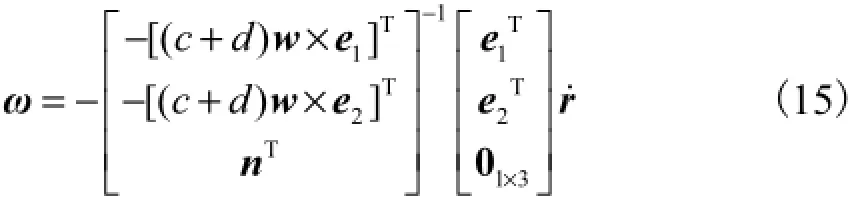
将式(15)代入式(8)，得到

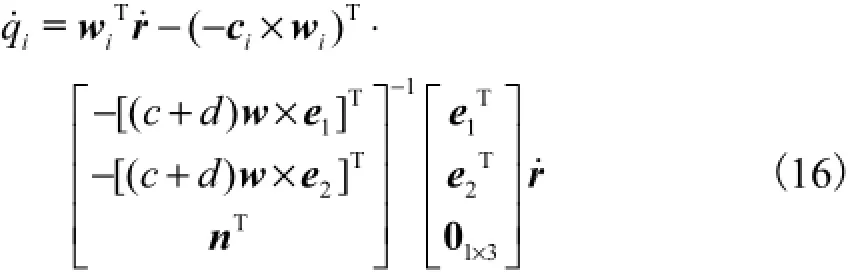
整理成矩阵形式，可得

式中Jq为3-UP S&PU并联动力头量纲统一的雅可比矩阵，其表达式为

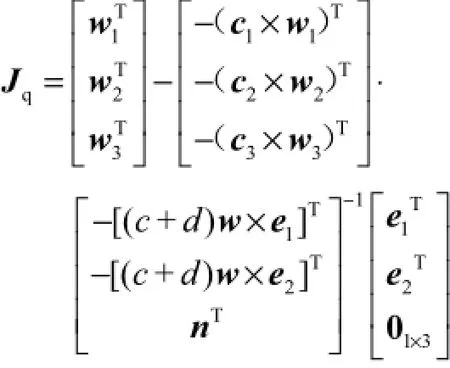
4 工作空间

4.1 可达空间与工作空间定义

根据3-UP S&PU并联动力头的运动特点，将其可达空间定义为对应于不同的z向平动，动平台可实现的姿态转角α、β的集合．其中，将具有恒定最大姿态转角的空间称为工作空间，设其高度为h0．指定的任务工作空间应包含在工作空间内，其高度应小于h0.

4.2 约束条件

为使3-UP S&PU并联动力头在工作空间内不发生奇异，定义

为保证动力头的刚度以及受驱动副自身行程的限制，需要对驱动支链的杆长加以约束，即

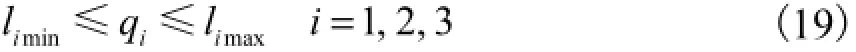
式中limin、limax分别为支链的最小、最大行程．

根据实际工程需求，3-UP S&PU并联动力头中球铰链的转角约束为

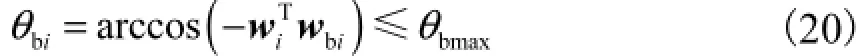
式中：biw为球铰链基座轴线的方向矢量，如图3所示；bmaxθ为球铰链的极限转角．图3中0θ为球铰链的安装角，其含义为biw与w所夹的锐角．

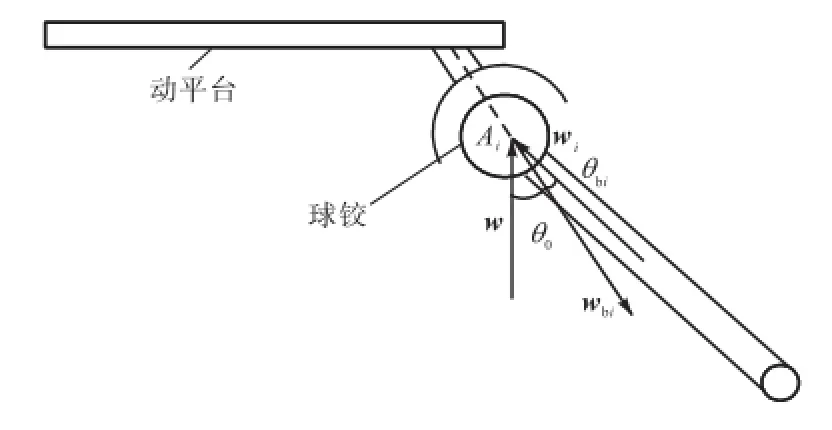
图3 球铰链安装角示意Fig.3 Schematic diagram of the setting angle of the spherical joint

虎克铰链转角的约束可定义为

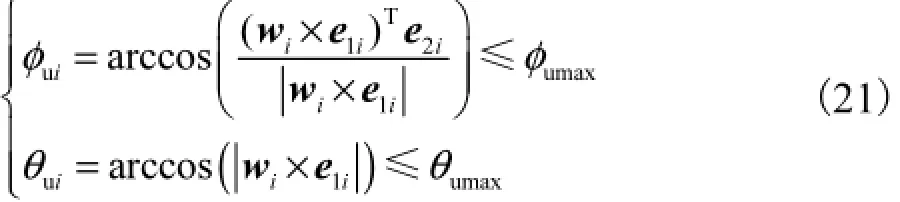
式中：1ie与2ie分别为沿ix轴与iy轴(i=1，2，3)正向的单位矢量；umaxθ、umaxφ分别为虎克铰内、外圈极限转角．

此外，为避免运动过程中相邻两连杆发生干涉，假设各连杆都是圆柱形，定义约束条件

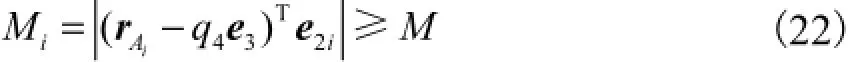
式中：rAi为点Ai在固定坐标系下的位置矢量；M为两连杆的截面半径之和；Mi为第i条UPS支链与PU支链中心线之间的最短距离．

4.3 算例仿真

3-UP S&PU并联动力头的尺度参数如表1所示.

表1 3-UPS&PU并联动力头尺度参数Tab.1 Dimensional parameters of the 3-UPS&PU parallel manipulator

针对3-UPS&PU并联动力头可达空间的特点，采用网格搜索法[11-12]这类数值方法搜索其可达空间．将动平台末端参考点C可能达到的位置定为目标搜索空间，将其沿固定坐标系的3个坐标轴方向进行离散化，得有限个网格节点．计算所有网格点对应位姿下的逆解，满足约束条件的即为可达空间内的有效点，记录该点的α、β、z值．图4即为搜索出的3-UPS&PU并联动力头的可达空间．

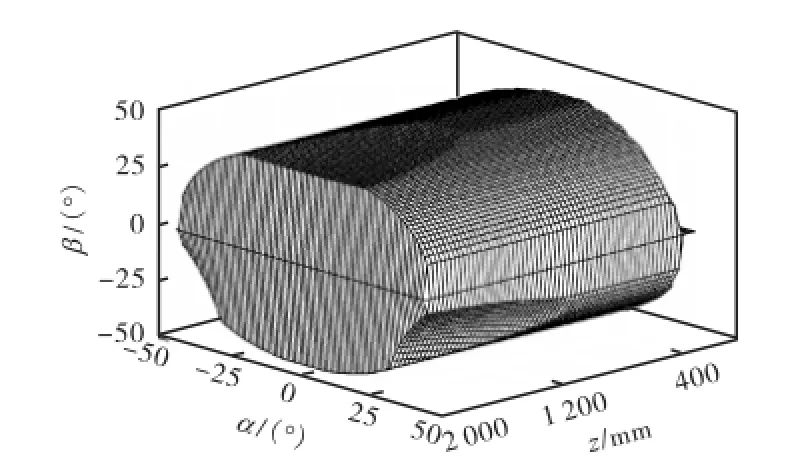
图4 3-UPS&PU并联动力头可达空间Fig.4 Reachable workspace of the 3-UPS&PU parallel manipulator

由如图4可见，该可达空间沿z轴前后两端为不规则形体，中间部分为一等截面柱体，且其截面上α、 β的最大值相等，该柱体即为工作空间．工作空间的高度h0即可达空间柱体部分的z向长度．由于工作空间横截面的形状、大小均不随结构参数的变化而改变，故h0可表征工作空间的体积大小．

4.4 机构尺度参数对工作空间的影响

本节通过改变3-UP S&PU并联动力头的参数，观察工作空间随参数的变化规律．

表2所示为给定b/a的范围1.00～2.75，且z= 200～2,000,mm时，工作空间的高度h0随b/a的变化情况．结果表明随着b/a的增大，h0先增加后减小.

表2 b/a=1.00～2.75时的工作空间高度Tab.2 Height of the workspace when b/a=1.00～2.75

表3所示为给定d/a的范围0～0.5，且当z= 200～2,000,mm时，h0随d/a的变化情况．结果表明，随着d/a的增大，h0逐渐降低．特别是当d/a≥0.2后，工作空间的高度开始锐减．

表3 d/a=0～0.5时的工作空间高度Tab.3 Height of the workspace when d/a=0～0.5

5 尺度综合

5.1 设计变量

给定3-UPS&PU并联动力头的任务空间Wt为：z∈[HH+h]，α、β∈[-40°40°]．其中，H为静平台中心O到Wt的最短距离，h为Wt的z向高度．为减少设计变量，实现系列化设计，将机构几何参数b、d、H均用动平台的半径a归一化，即令λ1=b/a、λ2=d/a、λ3=H/a．

5.2 性能评价指标

本文利用量纲统一的雅可比矩阵Jq的条件数的全域均值η和标准差σ构造出兼顾3-UPS&PU并联动力头在整个工作空间内运动性能平均水平和波动量的运动学性能指标f，将其作为优化设计的目标函数，即

式中wη为波动量σ相对于均值η的权重，使得两者在同一数量级上．因此，3-UP S&PU并联动力头的尺度综合问题可以归结为：给定相应的约束条件，确定无量纲的参数λ1、λ2和λ3，使得其性能指标f在给定的任务工作空间Wt中最小．

5.3 约束条件

参考第4.4节工作空间分析的结论，且考虑虎克铰链在静平台的安装尺寸，设定如下约束条件

为保证3条UPS主动支链具有足够的侧向刚度和精度，对其最大/最小杆长比施加如下约束条件：

式中：qimax和qimin分别为UPS支链的最大、最小杆长；μ0为μ的最大许用值．借鉴Tricept机械手的工程设计经验[13]，给出取值范围μ0=1.7～1.8，折中取μ0=1.75．从动支链PU同样存在杆长比问题，因此

考虑到PU支链为恰约束支链，需要承受的力(力矩)较大，侧向刚度要求比较高，这里取μ0=1.7．另外，λ4=h/H 为反映工作空间/机构体积比的因子，不宜太小．给定如下约束条件

若已给定/ha的值，3λ的上下限就可以确定了.此外，为避免动力头支链间发生干涉，各支链虎克铰与球铰的转角范围的约束条件为

虎克铰

球铰：

式中：θuimax、φuimax分别为第i条UPS支链虎克铰内、外圈绕其支承轴线转角的全域最大值；θu0和φu0分别为上述虎克铰内、外圈绕其支承轴线转角的最大许用值；θbimax为第i个球铰链的转角全域最大值；θb0为球铰链转角最大许用值．

5.4 优化设计

根据设计要求，给定θb0=θu0=φu0=45°、h/a= 3.33，而设计变量的取值范围可求解为：λ1=2～5，λ2=0～0.2，λ3=4.8～8.3．因此，3-UP S&PU并联动力头的尺度综合可以归结为求解如下有约束非线性规划问题，即

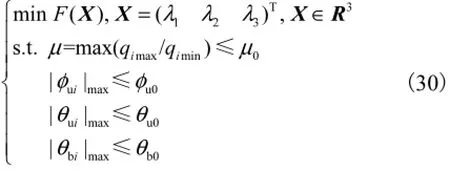
图5所示为μ、f、φu1max、|θu1|max随λ1、λ2、λ3变化的曲线．为将η和σ在同一数量级下衡量，经计算本文取wη=3．由于3-UPS&PU动力头拓扑结构以及任务工作空间都是关于z轴对称的，故φu1max的变化曲线与φu2max、φu3max相同，因而图5中只绘出了φu1max的变化曲线．而图5中只含有|θu1|max的变化曲线也是基于同样原因．由于球铰链的安装角θ0与工作空间的位置有关，故θbimax将在尺度综合后单独检验，这里不再绘出．由图中不难发现，μ、f、φu1max、|θu1|max均随λ3的增大而单调递减．此外，φu1max、θu1max在搜索可行域里均小于φu0，因此，上述参数不会在参数优化时起作用．图5(b)中，在设计变量x的可行域内，当λ1=2、λ2=0、λ3=8.3时，目标函数f取最小值，此时μ＜μ0．采用MATLAB遗传算法工具箱对该有约束非线性规划问题进行计算，所得结果与灵敏度分析的结果一致(见图6，a= 300,mm，b=600～1,500,mm，d=0～60,mm，H= 1,450～2,490,mm，即λ1=2～5，λ2=0～0.2，λ3= 4.8～8.3)，从而验证了该最优解的正确性．

同时，由图5(a)可知，给定λ1=2、λ2=0，满足主动支链的最大杆长比μ＜μ0约束的λ3的可行域为6.63～8.30．注意到当λ3≥6.63后，f随λ3的增大而下降的幅度不超过0.05．而H的增大会使机构的刚度以及工作空间与机构的体积比λ4降低．考虑机构的刚度和尺寸的合理性，本机构的设计采用以下方案，在不过多损失运动学性能的前提下，λ3可通过首先起作用的杆长约束，即

求解，得λ3=6.63，这样便可得到该问题的最优解．得到最优解之后，验证球铰的转角范围θb．在确定使θbimax最小的球铰链安装角θ0=9.1367°后，搜索得到3条主动支链球铰转角θbi在整个任务工作空间中的最大值约为42.850°，小于θb0．之后，可根据计算出的φu1max、θu1max进一步指导虎克铰的机械结构设计．计算表明|Jq|在任务工作空间均大于0，即无奇异点存在．

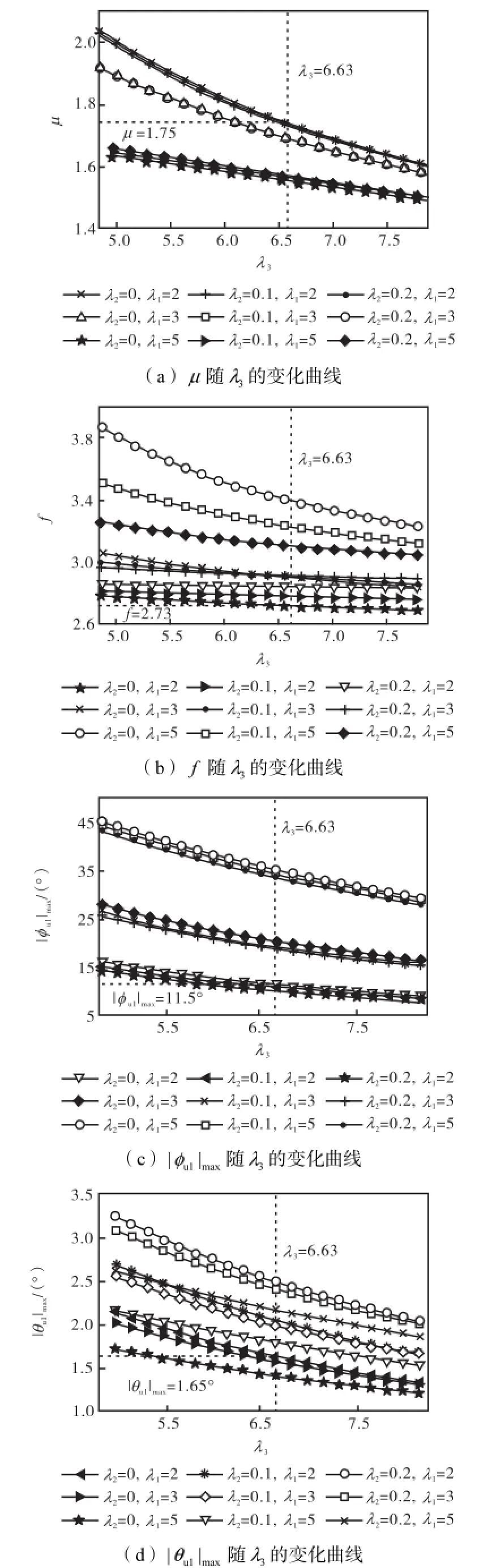
图5 μ、f、|φu1|max、|θu1|max随λ1、λ2、λ3的变化Fig.5 Variation ofμ，f，|φu1|max，|θu1|maxwith λ1，λ2，λ3

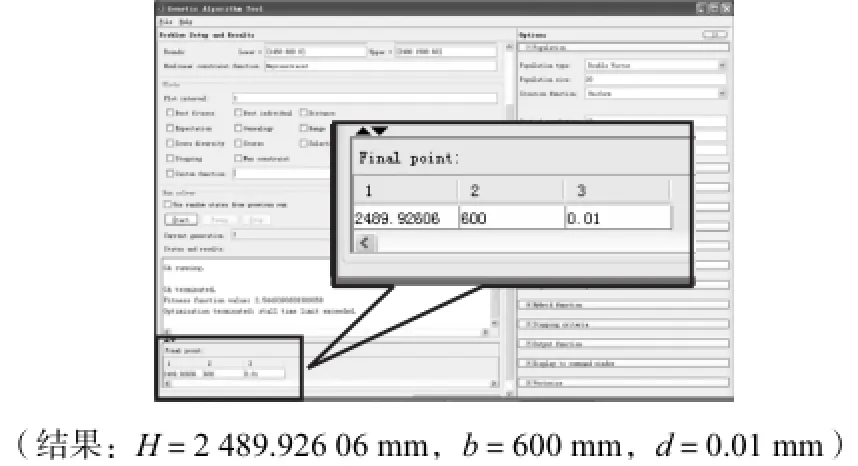
图6 利用MATLAB遗传算法工具箱的优化结果Fig.6 Optimal solution by MATLAB genetic algorithm toolbox

6 结 论

本文对一种含无约束支链和恰约束支链的1T2R并联动力头的运动学分析和设计开展了研究，得到如下结论：

(1) 利用闭环矢量法构造了3-UP S&PU并联动力头的位置逆解模型并得到量纲统一的雅可比矩阵，以其条件数构造出可同时兼顾全域内运动性能平均水平和波动量的评价指标．

(2) 借助数值搜索法得到了3-UP S&PU并联动力头的可达空间，并分析了设计参数对工作空间的影响规律，为尺度综合中约束条件的制定提供依据．

(3) 借助对一类有约束非线性规划问题的求解，完成了3-UP S&PU并联动力头的尺度综合．研究表明，λ2和λ1减小以及λ3增大时有利于提高3-UP S&PU并联动力头的运动学性能．但随着λ3的增大，动力头的工作空间与机构体积比及机构刚度会变差，因此，要求设计者根据具体使用情况权衡．

［1］ Neumann K E. Robot：US，4732525[P]. 1988-03-22.［2］ Wahl J. Articulated Tool Head：US，6431802[P]. 2002-08-13.

［3］ Li Q C，Hervé J M. 1T2R parallel mechanism without parasitic motion [J]. IEEE Transactions on Robotics，2010，26(3)：401-410.

［4］ Chi Z Z，Zhang D. Stiffness optimization of a novel reconfigurable parallel kinematic manipulator[J]. Robotica，2012，30(3)：433-447.

［5］ Zhang D，Gosselin C M. Kinetostatic modeling of n-DOF parallel mechanisms with a passive constraining leg and prismatic actuators[J]. ASME Transactions，Journal of Mechanical Design，2000，123(3)：375-381.

［6］ Tsai L W. Robot Analysis：The Mechanics of Serial and Parallel Manipulators[M]. New York：John Wiley & Sons Inc，1999.

［7］ Liu Haitao，Huang Tian，Mei Jiangping，et al. Kinematic design of a 5-DOF hybrid robot with large workspace/limb-stroke ratio[J] ASME Transactions，Journal of Mechanical Design，2007，129(5)：530-537.

［8］ Huang Tian，Li Meng，Li Zhanxian，et al. Optimal kinematic design of 2-DOF parallel manipulators with well-shaped workspace bounded by a specified conditioning index[J]. IEEE Transactions on Robotics and Automation，2004，20(3)：538-542.

［9］ Sun Tao，Song Yimin，Li Yonggang，et al. Dimensional synthesis of a 3-DOF parallel manipulator based on dimensionally homogeneous Jacobian matrix[J]. Science China Technological Sciences，2010，53(1)：168-174.

［10］ Huang T，Whitehouse D J，Wang J S. Local dexterity，optimum architecture and design criteria of parallel machine tools[J]. Annals of the CIRP，1998，47(1)：347-351.

［11］ 刘琳珊. 3-PRS并联机构设计方法研究[D]. 天津：天津大学机械工程学院，2007.

Liu Linshan. Research on Design Method of 3-PRS Parallel Mechanism [D]. Tianjin：School of Mechanical Engineering，Tianjin University，2007(in Chinese).

［12］ 黄 真，赵永生，赵铁石. 高等空间机构学[M]. 北京：高等教育出版社，2006.

Huang Zhen，Zhao Yongsheng，Zhao Tieshi. Advanced Spatial Mechanism[M]. Beijing：Higher Education Press，2006(in Chinese).

［13］ 李 曚. 可重构混联机械手TriVariant的设计理论与方法[D]. 天津：天津大学机械工程学院，2005.

Li Meng. Design Theory and Methodology of the Tri-Variant—A 5-DOF Reconfigurable PKM Module [D]. Tianjin：School of Mechanical Engineering，Tianjin University，2005(in Chinese).

(责任编辑：樊素英)

Kinematic Analysis and Optimal Design of a 1T2R Parallel Manipulator

Song Yimin，Zhang Jiateng，Sun Tao
(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China)

This paper presents the kinematic analysis and optimal design of a parallel manipulator with three degrees of freedom associated with one translation and two rotations(1T2R)，which may be applied to the high-efficient manufacturing of large aircraft structures. Firstly，the closed-loop vector method was used to establish the inverse position model，and then the homogeneous dimensional Jacobian matrix of the 1T2R parallel manipulator was obtained. The reachable workspace was acquired by the numerical search method，and the effect of key dimensional parameters on the workspace was demonstrated. Furthermore，the design parameters were normalized with respect to the radius of the moving platform of the 1T2R parallel manipulator. By using the condition number of the homogeneous dimensional Jacobian matrix，a global performance index was formulated taking into account the average and the standard deviation of kinematic performance in the prescribed workspace，whose combination can be chosen as the target function of dimensional synthesis. Finally，based on the engineering requirements and the workspace analysis results，the optimized design parameters were obtained through the sensitivity analysis after determining the constraint equations，which were verified by the genetic algorithm toolbox of MATLAB software. The researches of this paper can lay a solid foundation for more specific design of the 1T2R parallel manipulator.

parallel manipulator；kinematics；homogeneous dimensional Jacobian matrix；dimensional synthesis

TH122

A

0493-2137(2014)10-0863-08

10.11784/tdxbz201306004

2013-06-03；

2013-07-07.

国家自然科学基金资助项目(51075295，51205278，51135008)；高等学校博士学科点专项科研基金资助项目(2012003211003，2012003212003)；天津市应用基础与前沿技术研究计划资助项目(11JCZDJC22700，13JCQNJC04600).

宋轶民（1971— ），男，博士，教授，ymsong@tju.edu.cn.

孙 涛，stao@tju.edu.cn.

时间：2013-11-08.

http：//www.cnki.net/kcms/detail/12.1127.N.20131108.1059.003.html．