层叠绕组式磁悬浮永磁直流平面电机PID控制系统研究
张 钊,郭 亮
(浙江理工大学纳米测量技术实验室,杭州310018)
层叠绕组式磁悬浮永磁直流平面电机PID控制系统研究
张 钊,郭 亮
(浙江理工大学纳米测量技术实验室,杭州310018)
提出了一种层叠绕组式五自由度磁悬浮永磁直流平面电机的构想,针对该磁悬浮平面电机中的磁悬浮系统进行了控制系统设计。在对悬浮系统三维有限元分析的基础上利用参数辨识法构建了磁悬浮系统非线性模型;并利用微分几何方法,对磁悬浮模型进行完全精确反馈线性化,设计了PID控制器,并进行了样机控制实验。磁悬浮永磁直流平面电机悬浮高度的控制仿真和实验结果吻合度良好,系统稳态误差在1μm以内并具有优良的跟踪性能。
磁悬浮平面电机;微分几何法;反馈线性化;PID
0 引 言
在现代制造领域,超精密加工技术已经成为重要发展方向之一[1]。随着加工精度的不断提高,对精密加工定位平台定位精度、行程、运动自由度和工作环境等性能的要求也越来越严苛[2],传统二维定位平台以及接触式、气浮式平面电机驱动的定位平台越来越难以满足精密加工的要求。磁悬浮平面电机以其优越的运动定位性能,受到了越来越高的关注,将成为下一代超精密加工仪器的核心驱动部件。
磁悬浮平面电机是一个多输入多输出、非线性、耦合、参数摄动、抗干扰能力差的复杂系统,其高精密定位和多自由度运动的实现,在极大程度上取决于平面电机的结构与控制系统的设计,磁悬浮平面电机的发展也始终伴随着电机结构的创新和控制技术的进步。文献[3]中采用平衡点线性化和鲁棒控制控制相结合的磁悬浮控制系统设计方法,实现了磁悬浮系统平衡点附近的精确鲁棒控制;文献[4]中对于磁悬浮系统采用了平衡点线性化与非线性PID相结合的设计方法,扩大了磁悬浮系统精确控制的范围,但定位精度均随着与平衡点偏差的增大而降低,且鲁棒控制系统阶次高、增益大,数字控制器难以实现。
本文提出了一种结构简单、响应速度快、表面利用率高的层叠绕组式磁悬浮永磁直流平面电机结构,并对该平面电机的磁悬浮控制系统进行了设计与研究。在非线性系统控制系统设计过程中,采用完全反馈线性化方法[5],将非线性系统转化为线性系统,并在线性化后的系统模型基础上利用经典PID方法进行控制系统设计。
1 平面电机结构与工作原理
层叠绕组式磁悬浮永磁直流平面电机结构如图1所示,由空心绕组、定子永磁阵列和背铁组成。
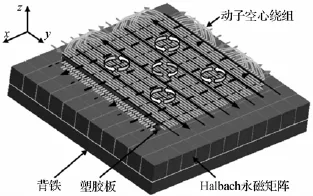
图1 磁悬浮平面电机模型
定子部分永磁体采用二维Halbach[6-8]永磁矩阵结构,由钕铁硼材料构成的永磁体模块和铁块组成,并通过背铁固定在磁悬浮隔震平台上。永磁矩阵具体组合形式如图2所示,本永磁体阵列除垂直充磁的磁极外,其余永磁体块均沿对角线方向充磁,充磁方向彼此连接以形成三维Halbach式结构,在背铁部分自成回路,以增强气隙部分的磁密。图2中通过形状相同的99块钕铁硼和12块铁块形成了彼此交错的4个N极、9个S极励磁磁场。平面电机动子部分采用层叠式空心绕组结构,由两层沿X方向铺设的绕组和两层沿Y方向铺设的绕组正交叠加构成。绕组连接方式如图1所示,每层绕组均由单匝导体铺设而成,每对极下的导体彼此串联,但相邻极间彼此并不相连,从而组成了多相的直流电机结构,以方便进行磁场的微调节,并进行多个自由度的调整[9]。

图2 定子永磁体充磁3D示意
当动子中绕组电流如图1中箭头所示时,即可构成所示的环流,形成与永磁体磁极分布结构相同的垂直磁极;各磁极磁通密度由所在区域等效电流中的直流分量决定,磁极位置由等效环流的位置决定,并随等效电流交流分量的变化而移动。统一调节空心绕组中的直流分量,调节动子磁极磁通密度,实现动子部分悬浮气隙微调,分别调节同方向排列的两侧多相绕组中的直流分量,破坏磁极磁通密度的对称性,实现动子部分绕x轴、y轴的旋转;统一调节相同排列方向绕组中的交流分量,调节等效环流的水平位置,实现动子沿x、y方向的水平运动。因此,该磁悬浮平面电机能够实现动子悬浮、二维平动以及绕x、y轴旋转,共5个自由度的运动。
2 平面电机磁悬浮系统模型
利用3D有限元分析方法对平面电机定子永磁矩阵上方的磁通密度进行分析,得到气隙高度为1 mm时水平和垂直气隙磁通密度分布曲线,分别如图3-图5所示,可以看到励磁磁场中z方向的各个垂直磁极以及x、y方向的水平分量均具有良好的对称性,若忽略绕组端部影响,当绕组电流分布均匀且关于永磁体中心线反向对称时,根据洛伦兹力定律可推知,导线的水平推力为0,垂直方向的悬浮力达到最大。

图3 x方向磁通密度3D曲线

图4 y方向磁通密度3D曲线

图5 z方向磁通密度3D曲线
取动子位移、速度和绕组电流为系统状态变量,根据洛伦兹力公式、运动学原理及电路原理,磁悬浮系统运动模型如下式所示,

其中:
m:动子部分质量,313.16 g;
l:磁场中每根直导线长度,每根直导线长度相同;
fd:系统干扰;
N表示在每根导线中心线上的磁通密度取点个数,Bjki表示第k层,第j根直导线中心线上所取第i个点的磁通密度。
利用有限元分析结果,计算在不同气隙高度下,单层直导线的值,得到随气隙高度变化表,如表1所示。
表1-气隙变化

表1-气隙变化
气隙高度/mm 磁密强度/T 0.5 12.285 7 1.0 10.944 7 1.5 10.232 6 2.0 9.429 1 2.5 8.729 4 3.0 8.155 9 3.5 7.505 3 4.0 6.985 6 4.5 6.493 8

其中:M、γ为待辨识参数;利用最小二乘法进行参数辨识,得M=1.402,γ=0.1503。
在控制器与磁悬浮平面电机空心绕组间加入电压控制电流源(VCCS)驱动器,使空心绕组中的电流按照比例关系随控制电压信号变化,则磁悬浮系统模型转变为如下形式:

令:f(x)=[x20]T,g(x)=[0 B/m]T;将重力加速度看作常值扰动,暂时不予考虑,则磁浮系统电流控制模型可以简化为式(4)的形式,是一个典型的单输入单输出二阶仿射非线性系统。

3 磁悬浮系统模型线性化
为实现磁悬浮系统的大范围精确控制,在磁悬浮系统模型线性化过程中采用基于微分几何理论的完全精确反馈线性化方法,将磁悬浮仿射非线性模型完全转化为串联积分形式的线性化系统模型。
对磁悬浮平面电机磁浮模型选取如下坐标变换:

则原系统模型可以转化为:

其中:
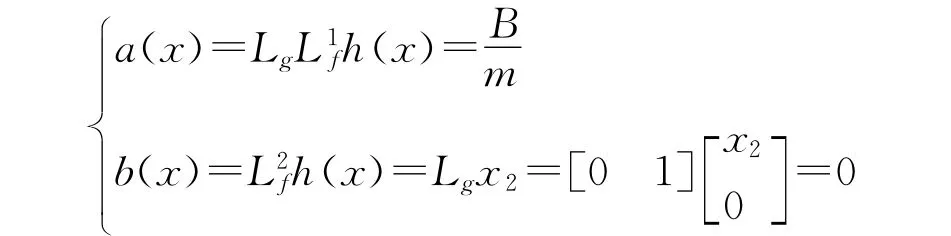
平面电机磁悬浮系统完全精确线性化模型如图6所示。

图6 磁悬浮系统完全精确线性化模型
4 PID控制系统设计与仿真
以基于微分几何理论的非线性反馈作为控制系统内环,将磁悬浮系统完全转化为线性系统,那么可以采用线性系统控制器设计方法设计磁悬浮控制系统。由于PID控制技术具有结构简单、参数调整方便、工作可靠、稳定性好、环境适应性强等优点[10],因此采用该技术构建不完全微分PID控制器,如图7所示。
其中:Kp,Ki,Kd分别为比例、积分、微分参数;T为惯性环节时间常量,取为0.000 5。
利用MATLAB/SIMULINK软件搭建平面电机磁悬浮PID控制系统仿真模型,如图8所示,其中零阶保持器sampletime为0.001s,两个单位延时代表实际数字控制器引入的系统延时。

图7 不完全微分PID控制器

图8 磁悬浮控制系统仿真模型
利用MATLAB/NCD参数寻优工具箱,结合控制系统模型进行PID离散控制系统仿真,得到PID参数如下:Kp=6.310 5、Ki=0.004 7、Kd= 0.028 1。其1 mm阶跃响应如图9所示,上升时间为0.015 s,超调为40%,稳定时间为0.1 s,静差为0,能够实现1 k Hz频率下的快速、无静差控制。
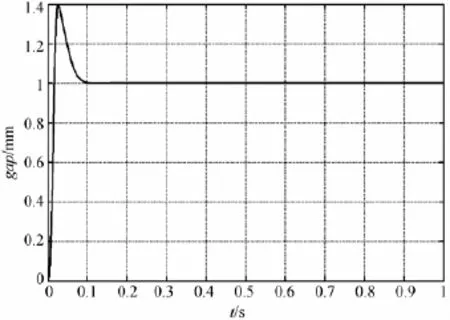
图9 PID控制系统阶跃响应曲线
5 实验与结果分析
为了验证理论分析结果并证实电磁悬浮的可行性,制造了样机并搭建磁悬浮系统控制实验平台。样机中动子表面积略大于永磁体,边长约为120 mm,四个角上利用滚珠式直线轴承与竖直导轨相连,导轨上安装涡流传感器实现悬浮高度的实时测量。利用MATLAB/RTW快速原型化xPC目标作为数字控制器,16位NI-6221为数据采集卡,KAMAN KD 2306为电涡流位移传感器,VCCS为磁悬浮系统驱动器,RC二阶低通滤波电路为反馈回路滤波器,搭建磁悬浮系统控制实验平台,如图10所示,其中xPC目标控制系统稳定实时运行频率为1 k Hz(本硬件条件下),VCCS驱动器电压-电流比例系数为0.489倍,零漂为0.002 7 A,RC二阶低通滤波电路截止频率为437 Hz。

图10 磁悬浮PID控制系统
利用MATLAB/SIMULINK搭建RTW控制框图,如图11所示,包括传感器信号处理、PID控制器、动子重力补偿、非线性系统反馈线性化、驱动器补偿等多个模块。

图11 磁悬浮PID控制器RTW模型
磁悬浮系统的1 mm阶跃响应如图12所示,可以看到在实际1 k Hz实时控制频率下,磁悬浮PID控制系统阶跃响应超调为24%,上升时间为0.018 s,稳定时间为0.12 s。
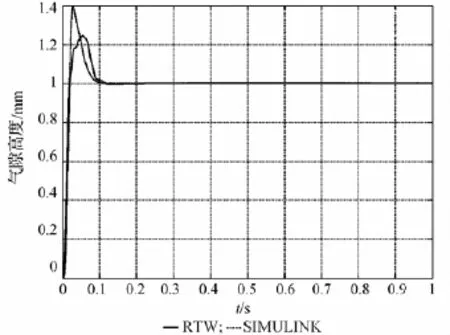
图12 控制系统1 mm阶跃响应仿真与实验对比
验证所设计的磁悬浮PID控制系统的控制精度,在1 mm气隙高度进行1μm的连续阶跃响应实验,如图13所示。
验证所设计控制系统的大范围控制精度,即验证磁悬浮系统完全精确线性化模型的线性化程度,在1.7 mm周围进行1μm的阶跃响应实验,如图14所示。
验证PID控制系统的大范围快速跟踪能力,在气隙1.3 mm下进行了峰-峰值为1 mm、频率为10 rad/s的正弦跟踪实验,如图15所示。
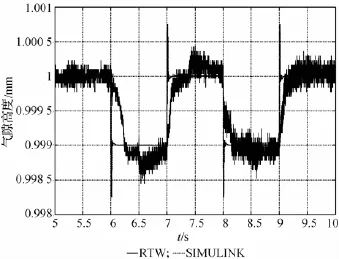
图13 控制系统1 mm周围1μm阶跃

图14 控制系统1.7 mm周围1μm阶跃

图15 控制系统1 mm正弦跟踪
对样机悬浮PID控制系统仿真与实验的数据进行对比。首先,在1 mm阶跃响应中系统上升过程和稳态过程两者结果几乎完全相同,但由于样机中直线轴承引入的摩擦力带来的阻尼效果,系统动态过程中超调量减小、稳定时间增加;其次,在系统连续1μm阶跃响应中,由于控制系统硬件条件限制和外部干扰,使得系统出现抖动,但不影响系统的稳态运行,且稳态精度小于1μm;再次,通过1 mm和1.7 mm两个气隙高度的1μm阶跃,可以看到完全线性化模型基础上设计的控制系统在实际运行中能够实现大范围的精确控制,验证了线性化模型的正确性。最后,控制系统1 mm峰-峰值的正弦跟踪实验中,可以看到系统仿真和实验结果曲线几乎完全重合,对比实验数据得到系统跟踪延迟小于0.015 s,跟踪小于40μm,具有较好的跟踪性能。
6 结 论
本文采用参数辨识方法建立了层叠绕组式永磁直流平面电机悬浮非线性系统模型,通过非线性反馈线性化和PID控制器相结合设计了控制系统。仿真和实验验证了所提出磁悬浮平面电机精密微运动的可行性,结果表明,建立的控制系统能够实现悬浮控制精度为1μm的大范围精确控制,并且具有优良的跟踪性能。
[1]袁巨龙,王志伟,文东辉,等.超精密加工现状综述[J].机械工程学报,2007,43(1):35-48.
[2]彭祎帆,袁 波,曹向群.光刻机技术现状及发展趋势[J].光学仪器,2010,32(4):80-84.
[3]Sinha P K,Pechev A N.Nonlinear H∞controllers for electromagnetic suspension systems[J].IEEE Trans. Automat Contr,2004,49(4):563-568.
[4]刘恒坤,郝阿明,常文森.磁悬浮系统的非线性PID控制[J].控制工程,2007,14(6):653-656.
[5]Hung J Y.Nonlinear control of a magnetic levitation system[C]//Industrial Electronics,Control and Instrumentation,1991:Proceedings IECON’91,1991 International Conference on.IEEE,1991:268-273.
[6]Jiang H,Zhou G,Huang X L,et al.Analytical force calculations for high precision planar actuator with halbach magnet array[J].IEEE Trans Magn,2009,45(10):4543-4546.
[7]Han Q,Ham C,Phillips R.Four-and eight-piece Halbach array analysis and geometry optimisation for Maglev[C]//Electric Power Applications,IEE Proceedings.IET,2005,152(3):535-542.
[8]Trumper D L,Kim W J,Williams M E.Design and analysis framework for linear permanent magnet machines[J].IEEE Trans Ind Appl,1996,32(2):371-379.
[9]Guo L,Chen B.Study on performances of novel electromagnetic drive micromanipulator[C]//Electrical Machines and Systems,2008:ICEMS 2008 International Conference on.IEEE,2008:3750-3753.
[10]毛 勇,控制电机转速的PID算法综述[J].机电信息,2011(6):43-44.
Study on PID ControI System of OverIapped Winding PMDC MagIev PIanar Motor
ZHANGZhao,GUO Liang
(Nanometer Measurement Lab,Zhejiang Sci-Tech University,Hangzhou 310018,China)
This paper proposes overlapped winding five-freedom-degree permanent magnet Direct-Current(PMDC)maglev planar motor and designs the control system in allusion to the maglev system in the planar motor.Based on 3D finite element analysis of the maglev system,this paper utilizes parameter identification method to construct nonlinear model of the maglev system.Besides,differential geometry method is used for complete accurate feedback linearization of the maglev model.PID controller is designed. Prototype control experiment is conducted.Simulation and experiment results of suspension height of PMDC maglev planar motor coincide well.The steady-state error of the system is less than 1μm and the tracking performance is excellent.
maglev planar motor;differential geometry;feedback linearization;PID
TP23,TP273.5
A
(责任编辑:康 锋)
1673-3851(2014)05-0525-07
2014-01-13
国家自然科学基金(51005213);浙江省自然科学基金资助(LY14E070008)
张 钊(1988-),男,山东枣庄人,硕士研究生,研究方向为纳米测量技术与仪器。
郭 亮,E-mail:lguo@zstu.edu.cn

