45钢薄壁圆柱管的冲击膨胀断裂机理研究＊

叶想平，李英雷，张祖根

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳621999）

金属壳体在冲击载荷作用下的断裂时间、断裂过程以及断裂结果预测是工程实践和武器研究中非常关注的问题。很多工程问题，例如：导弹、炮弹、壳体战斗部外壳的膨胀断裂，输油、输气管道和压力容器的爆裂；核电站防护层和管道材料的辐射脆化、热冲击安全、建筑物和结构中壳体部件抗冲击能力评估等，都涉及到结构的动态断裂性能评估和灾后对策问题，因此，金属壳体的动态断裂行为研究，一直受到人们的高度重视［1－8］。

目前，薄壁金属圆柱管膨胀断裂机理主要是依赖对最终断裂碎片的分析获得［2，4，6，8］。在低应变率下，G.I.Taylor［2］提出的径向拉伸断裂模式认为拉伸裂纹首先萌生于外壁面，而后始终沿径向向内壁面扩展，断裂模式为拉伸断裂模式；在高应变率下，C.R.Hoggatt等［7］提出的绝热剪切断裂模式认为，内壁面首先发生绝热剪切失稳，形成绝热剪切带向外扩展。当外壁面处于拉伸应力状态时，裂纹将沿剪切带向内扩展并最终断裂。随着应变率的降低，剪切方向的断裂带将不能贯穿整个壁厚，而是由拉伸裂纹首先沿径向向内壁面扩展一段距离遇到绝热剪切带后，才沿着绝热剪切带向内壁面扩展，形成拉剪混合断口［4，6］。另外，汤铁钢等［4］和胡八一等［8］的实验结果显示，减少壁厚或提高加载应变率，会出现拉－绝热剪切混合断裂向纯绝热剪切断裂的过渡。

针对现有高应变率加载的膨胀柱管实验难以冻结回收不同膨胀断裂阶段的金属柱管，对金属柱管动态膨胀断裂过程缺乏直观认识的问题［4－6，8－9］，本文中采用新发展得改进型霍普金森压杆冻结回收实验技术［10］，在中应变率（103s－1）下对45钢薄壁圆柱管进行膨胀断裂冻结回收实验研究。通过对不同膨胀断裂阶段的冻结回收样品的金相和扫描电镜显微分析，直接观察薄壁圆柱管在膨胀断裂过程中的裂纹萌生位置、萌生裂纹类型、裂纹后续扩展情况、最终断裂模式等演化特征，并考察加载应变率对其断裂机理的影响，为薄壁圆柱管冲击膨胀断裂机理研究提供直接的实验证据和分析补充。

1 实验描述

实验装置示意图如图1所示，在入射杆入射端添加一挡板，挡板后方为圆筒形制动块，圆柱管内填充石蜡。通过霍普金森压杆加载石蜡，对圆柱管进行径向膨胀加载。图1右边为实验部分放大示意图。调节入射杆端部挡板与制动块之间的距离，可实现对样品的单次可控脉宽加载，实现对样品的冻结回收［10］。通过调节加载弹速，可实现对样品加载的应变率控制。实验用圆柱管内径7 mm、外径8 mm、长10 mm，填充石蜡长6 mm，置于圆柱管中心位置。

通过冻结回收实验，可以一一得到圆柱管膨胀断裂过程中从发生塑性变形到裂纹在壁厚内演化、再到圆柱管发生完全断裂的整个过程，如图2所示。由于裂纹刚刚萌生时刻的回收样品很难在宏观照片中分辨出萌生状态，故未列出裂纹萌生时候冻结回收试样图片。

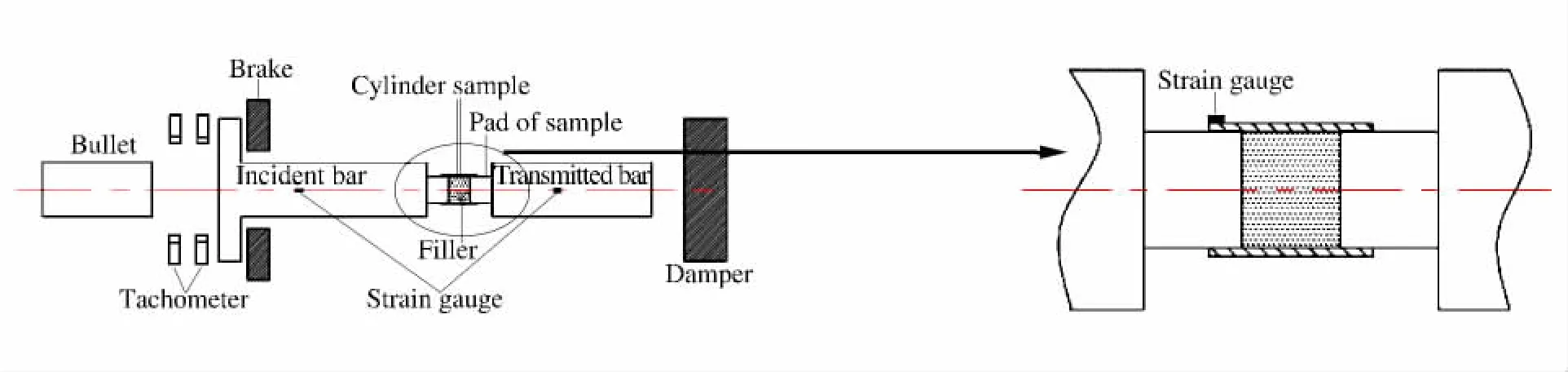
图1 实验装置示意图Fig.1 Schematic of experimental device

图2 冻结回收样品Fig.2 Pictures of freezing recovery sample

图3为圆柱管发生断裂时记录的原始波形图。如图3所示，在350μs处，二次加载波被制动块有效吸收，故未对样品进行二次加载，单次加载效果良好。圆柱管外壁端部环向粘贴的应变片用来监测圆柱管的加载时间t（圆柱管发生断裂时，即为其断裂时刻）［10］，如图3所示。通过直接测量冻结回收样品凸起最严重位置处的径向变形量（当圆柱管发生断裂后，测量轴向长度变形量，可换算得到径向变形量）可得到圆柱管凸起最严重位置处的径向应变（本文中应变和应变率均为圆柱管凸起变形最严重位置处的应变和应变率，后文中不再强调），结合加载时间，可得圆柱管径向加载应变率，由透射杆测量信号可得到圆柱管内压载荷，具体数据处理可参考文献［10］。

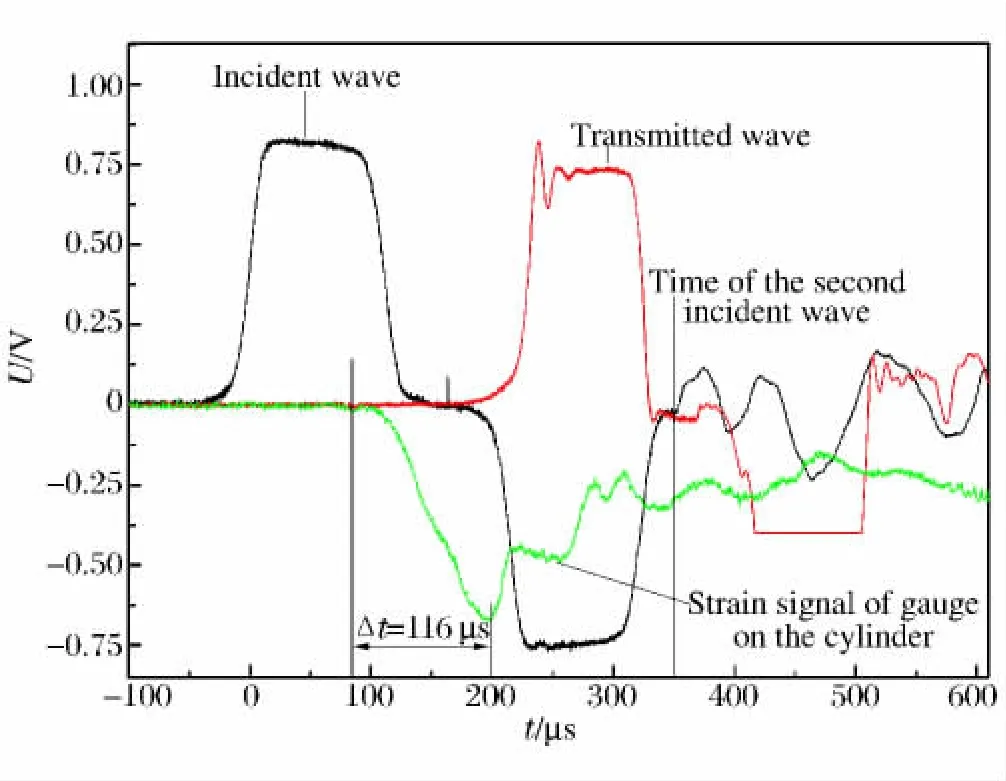
图3 某发实验原始电压波形图［10］Fig.3 Original voltage waveform of one experiment

2 实验结果

不同加载应变率下45钢圆柱管的膨胀断裂实验结果如表1所示。表中D为圆柱管实测初始外径，v为加载弹速，σn为石蜡内部压应力峰值，也是圆柱管内壁承受的载荷强度峰值，εr为圆柱管径向断裂应变，t为断裂时间，为圆柱管径向应变率。表1中实验结果表明，在实验应变率范围内，提高加载应变率（内压载荷峰值从134 MPa提高到145 MPa），圆柱管内部损伤演化程度加剧，损伤演化速率更快，表现为宏观径向断裂应变增加、断裂时间缩短，断裂模式由拉剪混合向纯剪切过度。实验结果与化爆圆柱管实验结果一致［4］。

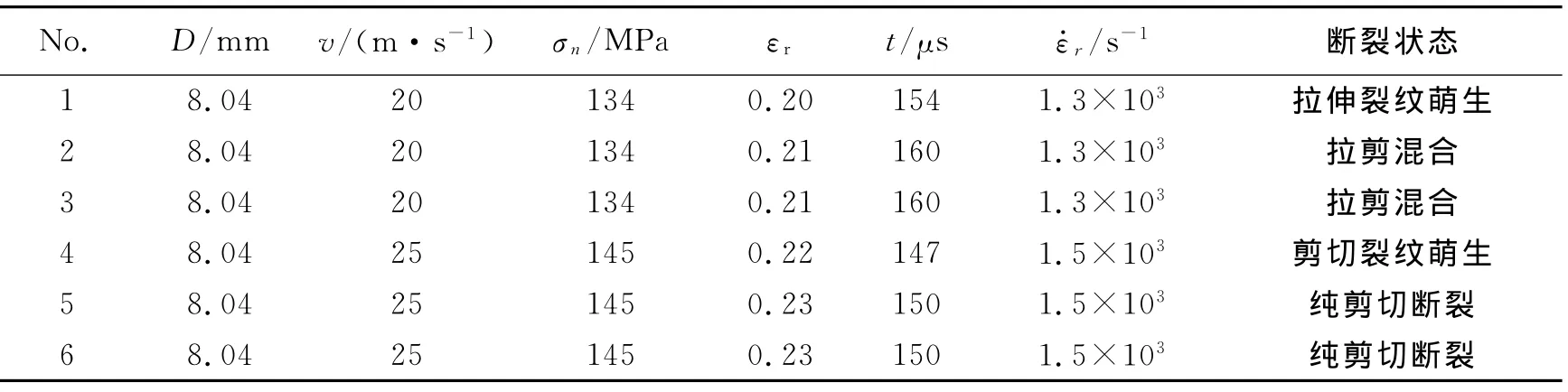
表1 圆柱管在不同加载应变率下的实验结果Table 1 Experimental results of cylinder shells under different strain－rate

3 机理分析

圆柱管膨胀断裂机理研究主要借助于金相显微技术手段，观察不同断裂演化阶段的冻结回收圆柱管的断裂特征。为了便于观察，每幅有裂纹的金相图片边角上都配有裂纹（或断口）位置示意图，如图4所示。对圆柱管膨胀断裂全过程的观察结果和分析如下。

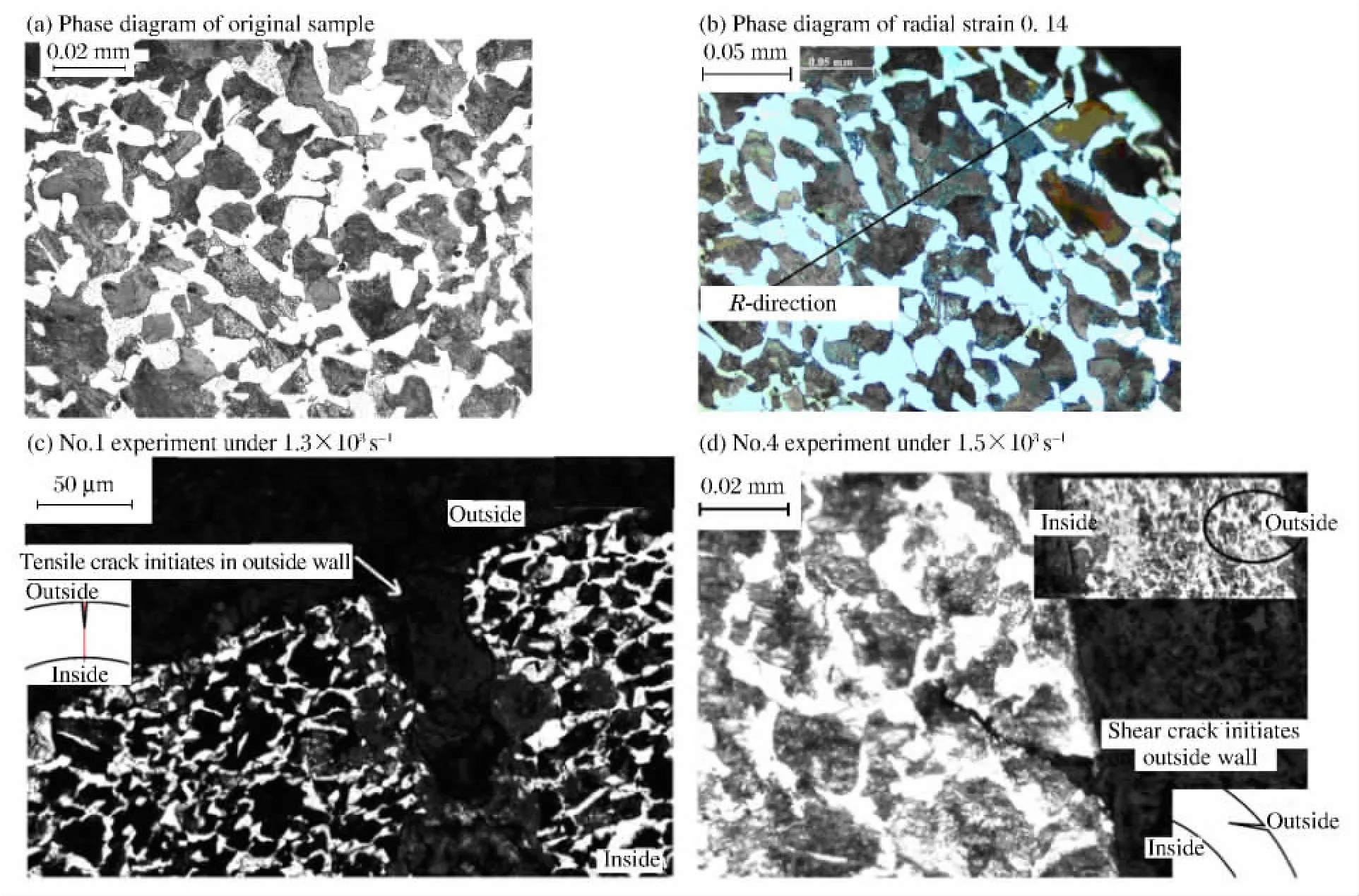
图4 圆柱管裂纹起始位置与扩展形式Fig.4 The propagation route and starting position of crack on cylinder shells

3.1 裂纹萌生位置与形式

在初始时刻，45钢圆柱管样品中的珠光体和铁素体基本处于均匀分布状态，如图4（a）所示；圆柱管受内部压力载荷作用后，内部晶粒首先被环向拉伸，如图4（b）所示。在加载持续作用下，拉伸裂纹将萌生于外壁面，如图4（c）所示。加载圆柱管内部压力峰值载荷从134 MPa增加到145 MPa、加载应变率随之增高后，圆柱管膨胀断裂萌生前，仍旧是内部晶粒首先被环向拉伸，与图4（b）所示类似，因此没有重复展示图片；延长加载时间后，裂纹将以剪切形式萌生于外壁面，但剪切裂纹前端并没有绝热剪切带，如图4（d）所示。裂纹萌生形式由拉伸向剪切过渡的临界加载应变率为1.5×103s－1。在实验加载应变率条件下，圆柱管在膨胀断裂过程中，裂纹萌生于外壁面，并随加载应变率的提高，裂纹萌生形式由拉伸向剪切过渡，但剪切裂纹前端未观察到绝热剪切带，表明绝热剪切带并非纯剪切断裂的必要条件。C.R.Hoggatt等［7］提出的绝热剪切断裂模式并不能解释所有纯剪切断裂。裂纹萌生形式随加载应变率的增加由拉伸向剪切裂纹过渡的具体机理还有待进一步研究。

3.2 裂纹扩展与断裂模式

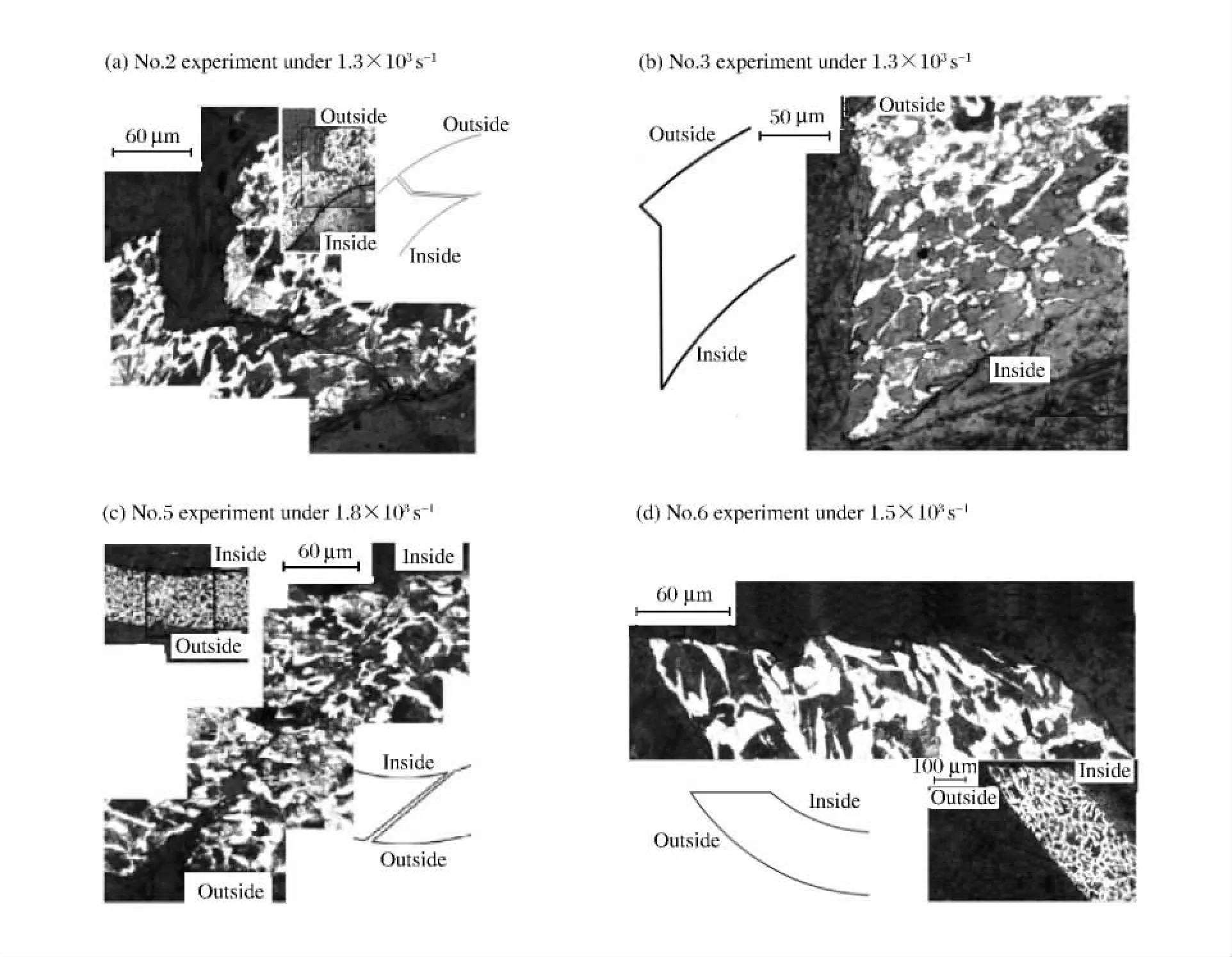
图5 圆柱管在不同加载应变率下裂纹扩展形式与断口形貌Fig.5 The route of crack propagation and fracture surface morphology of cylinder shells at different strain rates

实验加载应变率范围内，当加载应变率较低（1.3×103s－1，内压载荷峰值134 MPa）时，萌生的拉伸裂纹先沿径向扩展一段距离后，转而沿剪切方向向内壁面扩展，如图5（a）所示。裂纹张开宽度在外壁面比内壁面大，这也再次表明，圆柱管在膨胀断裂过程中，裂纹起始于外壁面。当裂纹贯穿整个壁厚，圆柱管完全断裂后，断口呈拉剪混合型，如图5（b）所示，断裂时间t＝160μs，对应断裂应变为0.21。图5（a）～（b）中剪切断口部分均没有观察到晶粒严重滑移带，进一步表明拉剪混合断裂过程中，并没有绝热剪切带的存在。由于载荷能量限制，断口处产生的卸载波迅速对整个圆柱体进行卸载，其余部位来不及积累更多的损伤产生裂纹，从而抑制了多裂纹的产生。提高加载应变率到某临界值附近（1.5×103s－1，内压载荷峰值145 MPa），萌生的剪切裂纹将一直沿剪切方向向内壁面扩展，直至贯穿壁厚，如图5（c）所示。同样，裂纹张开宽度在外壁面比内壁面大。当裂纹贯穿整个壁厚，圆柱管发生断裂后，断口呈纯剪切型断口，如图5（d）所示。断裂时间t＝150μs，断裂应变为0.23。图5（c）～（d）的纯剪切断口剖面中均未观察到晶粒严重滑移带，进一步表明纯剪切断裂过程中，并没有绝热剪切带的存在。断裂模式从拉剪混合向纯剪切过渡的临界加载应变率在1.5×103s－1左右，说明薄壁金属圆柱管在冲击膨胀断裂过程中，断裂模式随加载应变率的提高存在从拉剪混合断裂模式向纯剪切断裂模式的转变，但此处的剪切断裂并不是绝热剪切断裂。而这种断裂演化模式随加载应变率的提高发生转变的具体机理原因还有待进一步研究。

4 结 论

通过基于SHPB装置的冻结回收实验技术，研究了45钢圆柱管在内部动载下的膨胀断裂特性。在中应变率范围内，得出以下结论：

（1）通过冻结回收实验技术，观察到了包含裂纹萌生、扩展直至断裂的圆柱管冲击膨胀全过程。

（2）圆柱管在膨胀断裂过程中，裂纹萌生于外壁面。随着加载应变率的提高，裂纹萌生形式由拉伸裂纹逐渐向剪切裂纹转变；在较低应变率下，拉伸裂纹萌生于外壁面后，先沿径向扩展，而后转而沿剪切方向扩展，最终断裂模式为拉剪混合断裂；在较高应变率下，剪切裂纹在外壁面萌生后，会一直沿剪切方向向内壁面扩展，最终断裂模式为纯剪切断裂模式。圆柱管断裂模式由拉剪混合向纯剪切转变的临界加载应变率在1.5×103s－1左右。

（3）圆柱管膨胀变形及断裂过程中未见绝热剪切带的孕育，与高应变率下圆柱管的膨胀断裂机制存在显著差异。

［1］Mott N F.A theory of fragmentation of shells and bombs［M］∥Fragmentation of Ring and Shells.Springer Berlin Heidelberg，2006：243－294.

［2］Taylor G I.The fragmentation of tubular bombs［C］∥Batchelor G K.The Scientific Papers of Sir Geoffrey Ingram Taylor：Vol.3.Cambridge：Cambridge University Press，1963：387－390.

［3］马晓青.冲击动力学［M］.北京：北京理工大学出版社，1992：282－294.

［4］汤铁钢，李庆忠，孙学林，等.45钢柱壳膨胀断裂的应变率效应［J］.爆炸与冲击，2006，26（2）：35－39.Tang Tie－gang，Li Qing－zhong，Sun Xue－lin，et al.Strain－rate effects of expanding fracture of 45 steel cylinder shells driven by detonation［J］.Explosion and Shock Waves，2006，26（2）：35－39.

［5］汤铁钢，李庆忠，陈永涛，等.实现材料高应变率拉伸加载的爆炸膨胀环技术［J］.爆炸与冲击，2009，29（1）：45－46.Tang Tie－gang，Li Qing－zhong，Chen Yong－tao，et al.An improved technique for dynamic tension of metal ring by explosive loading［J］.Explosion and Shock Waves，2009，29（1）：45－46.

［6］汤铁钢，谷岩，李庆忠，等.爆轰加载下金属柱管膨胀破裂过程研究［J］.爆炸与冲击，2003，23（6）：529－533.Tang Tie－gang，Gu Yan，Li Qing－zhong，et al.Expanding fracture of steel cylinder shell by detonation driving［J］.Explosion and Shock Waves，2003，23（6）：529－533.

［7］Hoggatt C R，Recht R F.Fracture behavior of tubular bombs［J］.Journal of Applied Physics，1968，39（3）：1856－1862.

［8］胡八一，董庆东，韩长生，等.内部爆轰加载下的钢管膨胀断裂研究［J］.爆炸与冲击，1993，13（1）：49－54.Hu Ba－yi，Dong Qing－dong，Han Chang－sheng，et al.Studies of expansion and fracture of explosive－filled steel cylinders［J］.Explosion and Shock Waves，1993，13（1）：49－54.

［9］Grady D E，Benson D A.Fragmentation of metal rings by electromagnetic loading［J］.Experimental Mechanics，1983，23（4）：393－400.

［10］叶想平，李英雷，李英华.基于SHPB装置的膨胀圆柱管实验技术［J］.爆炸与冲击，2012，32（5）：528－534.Ye Xiang－ping，Li Ying－lei，Li Ying－hua.An experimental technique for expanding of metal cylinder based on the SHPB［J］.Explosion and Shock Waves，2012，32（5）：528－534.