微结构对多孔材料应变率效应影响的机理研究＊

王鹏飞，徐松林，李志斌，胡时胜

（中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽 合肥230027）

多孔金属是具有一定孔隙度的结构型材料，在实验探讨多孔金属的应变率效应时，则需将轴向惯性效应与应变率效应解耦，使两端的应力几乎相等，即满足应力应变均匀的基本假定［1］。

多年来，关于多孔金属的应变率效应研究的文献众多，多数学者［2－4］指出多孔金属材料具有明显的应变率效应，可将引起应变率效应的原因归结为以下因素：基体材料的应变率效应、微结构的惯性、孔内气体等。其中胞孔结构变形引起的微惯性影响是主要的一个因素，并对此进行了较系统的讨论。如C.R.Calladine等［5］和L.L.Tam等［6］利用2种典型的结构解释了这种由微结构惯性引起的强度增强现象，如图1所示，TypeⅠ（圆环）和TypeⅡ（折板）。如图1（b），TypeⅠ圆环结构在准静态压缩下力－位移曲线具有一个“平台”，动态压缩时微惯性的影响较小，此类结构呈现出率不敏感现象；TypeⅡ折板结构存在一个显著的力下降现象（即结构失稳），在高速撞击时强度增加，率敏感性较强，且随着折板角度（即缺陷大小）的增加，微惯性的影响降低。

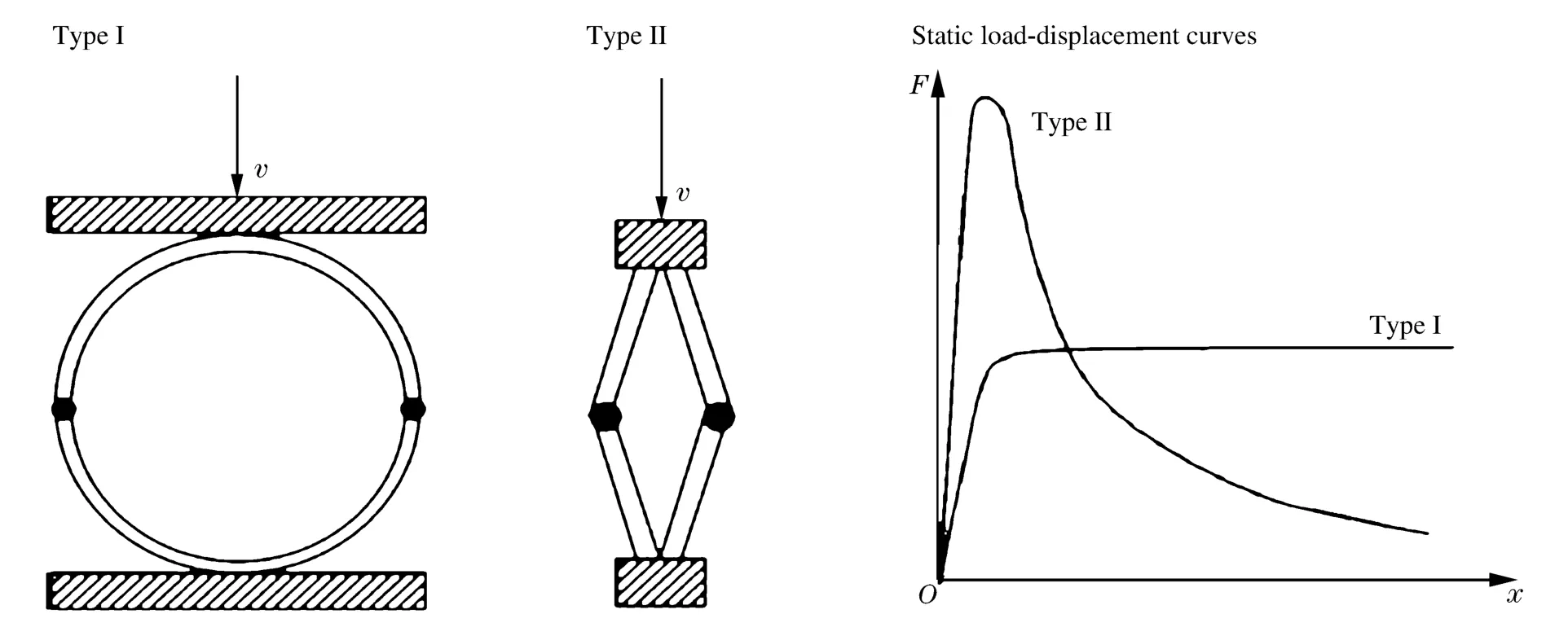
图1 2种类型的率敏感结构［5］Fig.1 Two types of velocity sensitive structures［5］

H.Zhao等［7］指出蜂窝铝在面外方向（垂直于六边形孔面的方向）压缩时的力学行为与TypeⅡ折板结构类似，采用单臂塑性铰简化模型从横向惯性保护的角度对结构动态应力增强现象给予简单的物理解释，对于此TypeⅡ折板结构的率敏感性问题已经得到众多学者的认可与理解。同时，H.Zhao［7］等也指出铝蜂窝在面内方向（平行于六边形孔面的方向）冲击加载下没有显著的增强效应，呈现率不敏感的现象，类似于TypeⅠ圆环结构。C.Chen等［8］和J.L.Grenestedt［9］认为商业泡沫铝包含众多缺陷并且由胞壁的弯曲变形占主导地位，因此泡沫金属中微结构的惯性效应所起的作用并不大。V.S.Deshpande等［10］和K.Y.G.Mccullough等［11］均认为商用泡沫金属材料类似于TypeⅠ圆环结构的特性，应力应变曲线伴有“平台”，且应变率不敏感。之前，X.L.Dong等［12］通过三维薄壁球壳实验指出其在静态压缩下呈现五边形状凹陷，动态压缩下呈现四边形状的凹陷，可见球壳结构在动静态下的变形模式是不同的。

本文中主要在前人的基础上利用数值模拟重点对TypeⅠ圆环结构的应变率不敏感二维模型进行一些补充理解，更直观地指出无论对于TypeⅠ（圆环）结构还是TypeⅡ（折板）结构，只要存在结构的屈曲失稳，就一定具有应变率效应。并通过三维蜂窝结构的模型更清楚地揭示微结构对多孔材料变形过程的影响。

1 TypeⅠ圆环结构的率效应

1.1 模型的建立

在前人讨论的基础上，通过Abaqus/Explicit有限元方法建立简单的二维圆环压缩模型，对其应变率效应机理做进一步的验证与分析。

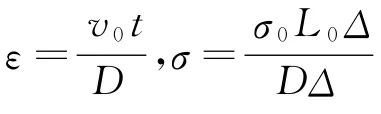
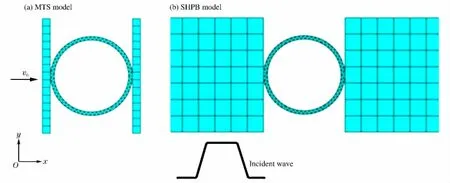
图2 准静态和动态加载模型Fig.2 Load models under quasi－static and dynamic

采用三角形网格单元，单元尺寸0.5 mm，圆环的材料采用的是应变率无关的弹塑性模型（2024铝合金）：

式中：A＝265 MPa，B＝426 MPa，n＝0.34。

1.2 圆环结构的应变率效应

根据上述模型模拟得到的名义应力应变曲线如图3所示。可以看出，在“Ⅰ－1”区圆环压缩的过程中应变率效应不明显，如同图1（b）中TypeⅠ的力－位移曲线，光滑而呈平台特性，此时结构引起的应变率效应并不明显。但是当应变大于0.45时，应力则随着应变率的升高而增加，如图3中“Ⅰ－2”区。由此可知，此圆环结构在初始压缩时无应变率效应，但是在变形的后期呈现一定的应变率效应。

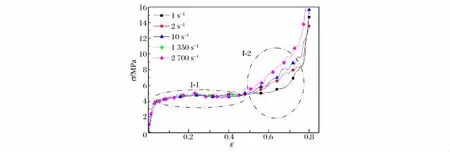
图3 圆环结构的名义应力应变曲线Fig.3 Normal stress－strain curves of ring structure

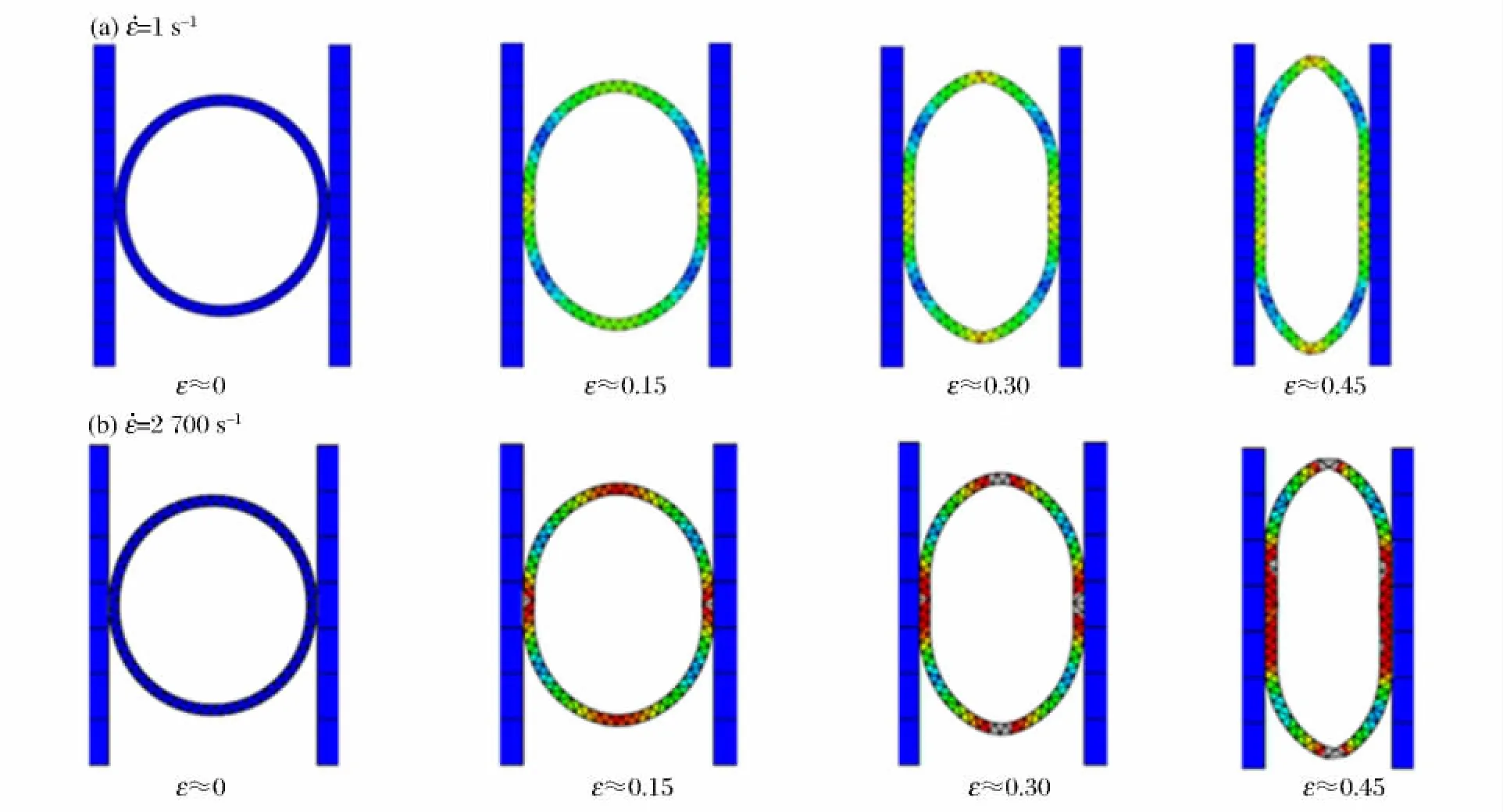
图4 圆环结构的变形过程图（ε≤0.45）Fig.4 Deformation process of ring structure（ε≤0.45）

但是当应变大于0.45时，圆环在压缩过程中不再是轮廓的塑性弯曲，而是伴着后续阶段的屈曲失稳。随着应变率的增加，失稳屈曲的模式也有所变化，如图5所示，圆环在压缩过程的后续阶段，从低应变率下的非对称变形逐渐变成高应变率下的对称变形，屈曲模式的不同导致其在不同的应变率下力学响应的不同。即使屈曲均为对称变形（如图5中和，也会存在屈曲开始时间的差异，导致在高应变率下具有更高的强度。

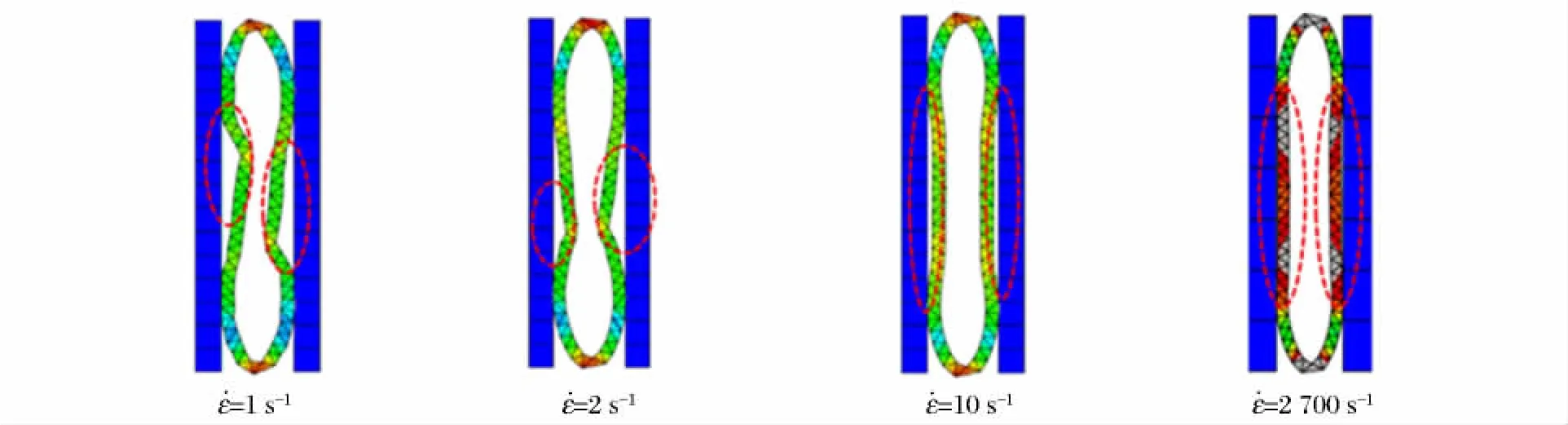
图5 不同应变率下的屈曲失稳模式（ε≈0.72）Fig.5 Buckling models under different strain－rate（ε≈0.72）

由于惯性倾向于抑制更柔顺的屈曲模式［12］，在低应变率压缩时，结构在变形过程中有足够的时间运动，惯性效应不明显，结构整体的“柔度”较高。但在高应变率压缩时，需满足运动协调条件，惯性效应显著，因此在高应变率下相当于降低了结构的“柔度”，高应变率下结构“柔度”的降低导致其屈曲模式也会有所差异，而“柔度”较低下的屈曲模式对应着更高的力学响应，这就是圆环结构在后屈曲阶段应变率敏感的原因。

在数值模拟圆环的压缩变形过程的同时，还讨论了网格尺寸对模拟结果的影响。降低网格的尺寸（0.05、0.025、0.01 mm），均存在屈曲模式随应变率增加而变化的现象，如图6所示，当网格细化到0.05 mm时，低应变率下（见图6（a））结构“柔度”相对较高，容易失稳，而高应变率下（见图6（b））结构“柔度”较低，不易失稳。表明不同的网格大小对结果规律的影响不大。

图6 圆环结构的变形过程图（H＝0.5 mm，D＝10 mm，网格尺寸0.05 mm）Fig.6 Deformation process of ring structure（H＝0.5 mm，D＝10 mm，grid size 0.05 mm）

在单个圆环的压缩过程中，薄壁（H＝0.5 mm）圆环易屈曲失稳（见图6（a））。随着壁厚H 增加到1、2 mm（图7（a）、（b）），环壁在压缩的过程中失稳的现象越来越不显著，此时结构屈曲导致的应变率效应也逐渐不明显。从图7（c）中可以看出，此时环壁较厚（H＝3 mm），并没有明显的屈曲现象。

对微观机理的研究可以探知其宏观力学响应，折板结构的失稳现象较为显著，而圆环结构的屈曲失稳往往发生在压缩过程的后期，单个圆环的后屈曲阶段几乎伴随着多孔材料的整个压缩过程，这种后屈曲阶段的率敏感性必然对多孔材料的率效应产生影响，但对于不同孔径、不同密度的多孔材料，微结构对其应变率效应的影响程度是不同的。

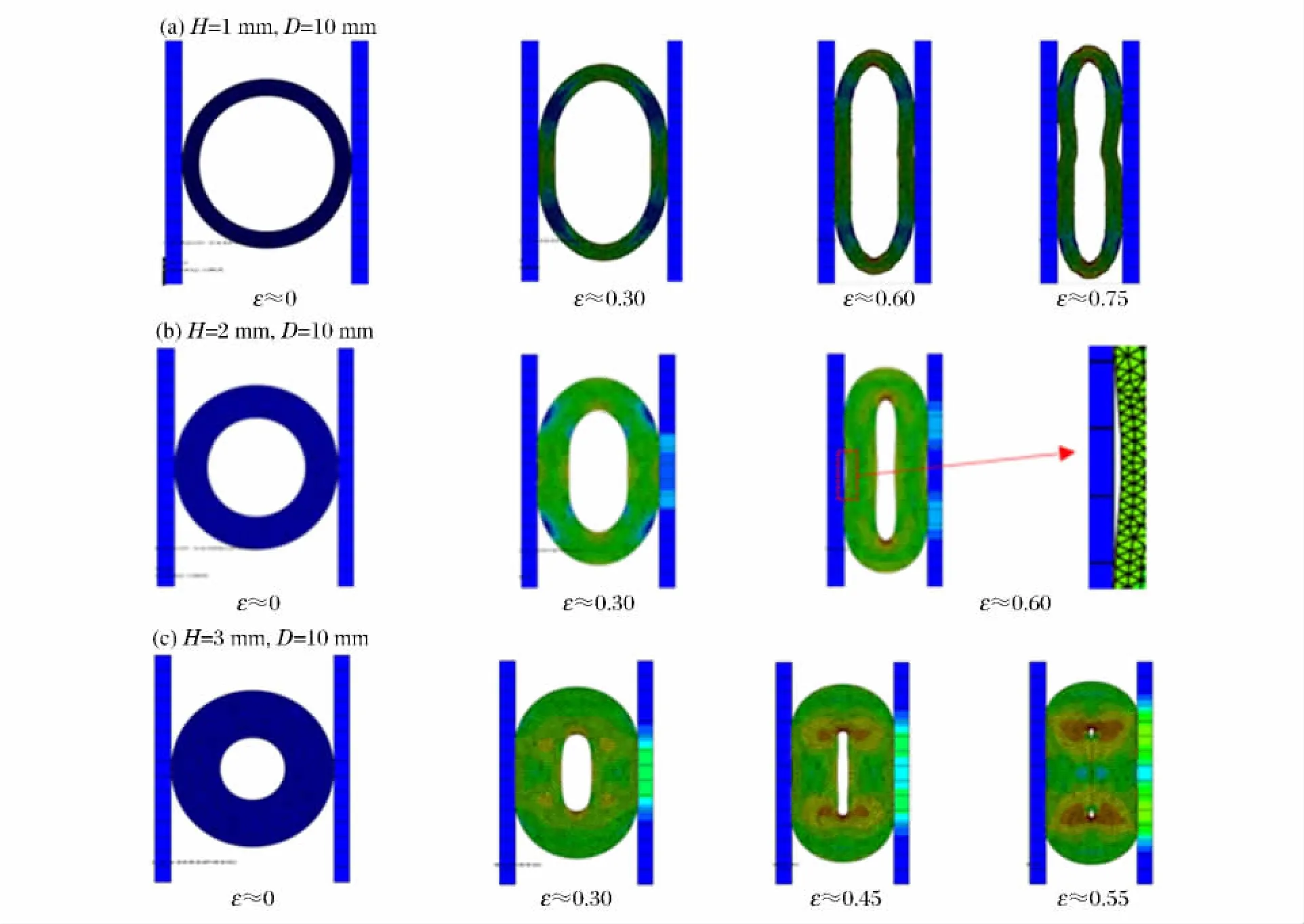
图7 不同壁厚的圆环变形过程图（＝10 s－1）Fig.7 Deformation process with different wall thickness（＝10 s－1）

2 蜂窝结构的应变率效应

前面讨论了单个圆环结构的屈曲失稳引起的应变率效应，接下来建立圆环蜂窝状结构模型进一步讨论多孔结构的应变率效应，试图更清楚地揭示微结构引起的应变率效应。

利用Abaqus建立的蜂窝结构如图8所示，圆环直径2.8 mm，最小棱壁厚0.2 mm，面内拉伸20 mm生成蜂窝结构，建立1/4体模型。采用六面体形状网格，网格尺寸0.2 mm。同样采用式（1）给出的应变率无关的弹塑性模型，利用无震荡的梯形波脉冲从入射杆端部加载。

图8 圆形蜂窝结构的SHPB模型Fig.8 SHPB model of circular honeycomb

如图9（a）所示，从名义应力应变曲线上可以看出，在压缩的初始阶段，应变率效应不明显，但是在虚线区域内，随着应变率的提高，第1个峰谷处对应的应变增加、应力也提高，在此段呈现一定的应变率效应。

图9（b）是在4 500 s－1加载下SHPB透射杆中的应力－时间曲线。在80μs时，如图9（d）中虚线，紧靠前端面的孔壁圆环向内屈曲，此时应力也下降（对应图9（b）中透射波信号），可见应力下降由此孔壁屈曲所导致。在稍低应变率（如800 s－1）加载下，紧靠左端面的圆环在压缩时先发生屈曲失稳，屈曲层有足够的时间继续运动，因此应力下降的值相对较大。但是在更高应变率（4 500 s－1）下，同样是紧靠左端面的圆环层屈曲，屈曲层需要满足运动协调条件，于是在应力应变曲线（图9（a））上表现出比800 s－1更高的强度，即应力下降的值相对较小。

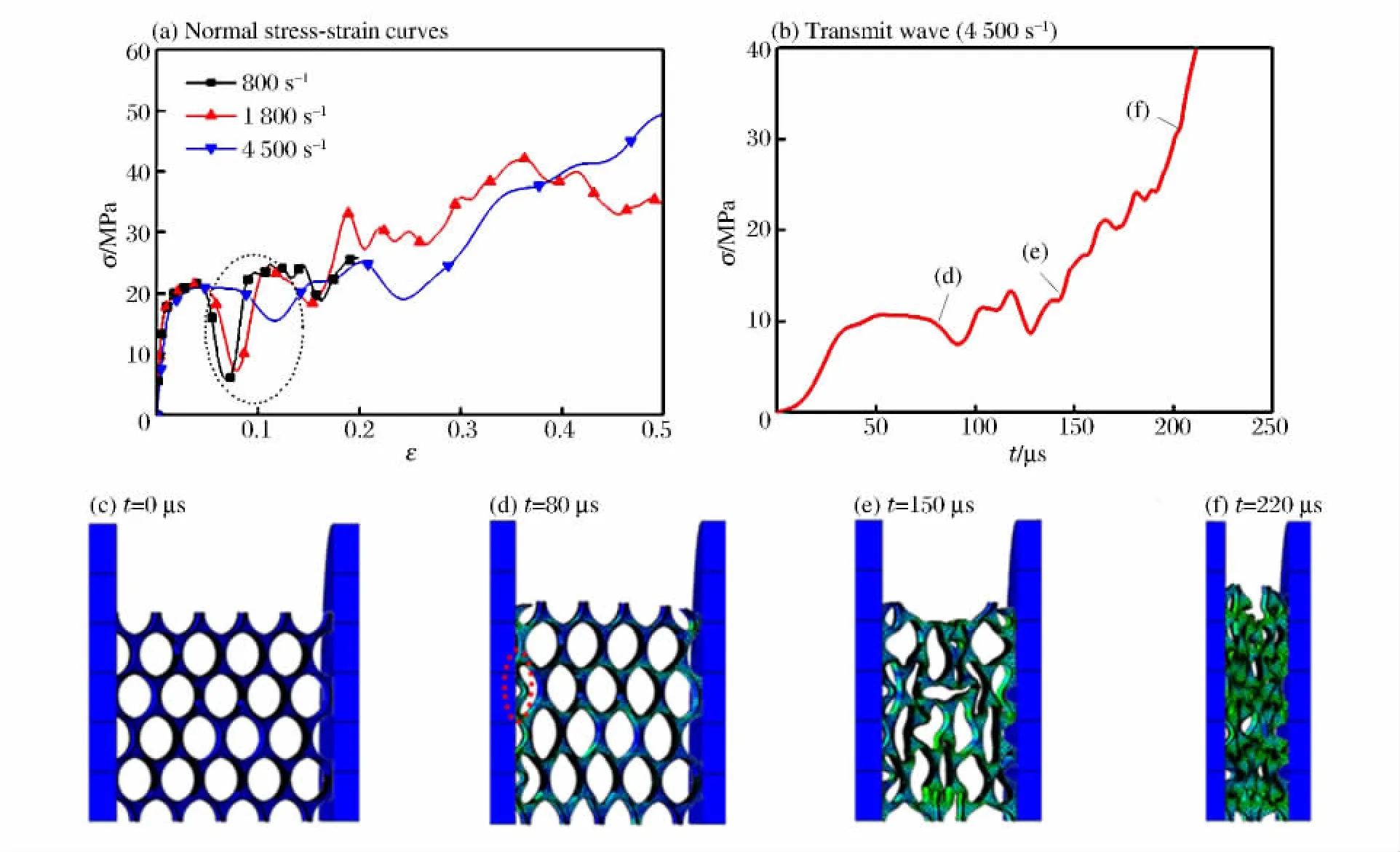
图9 圆环蜂窝的应变率效应Fig.9 Strain－rate effect of circular honeycomb

3 结 论

主要通过数值手段讨论了单个圆环结构对多孔金属应变率效应的影响。从2种典型的基本结构出发，指出无论是对于TypeⅠ（圆环）结构还是TypeⅡ（折板）结构，只要存在结构的屈曲失稳，就一定具有应变率效应，薄壁圆环（球壳）在后屈曲段也具有明显的应变率效应。随着圆环壁厚的增加，在加载过程中越不易坍塌失稳，此时微结构所引起的应变率效应也就越不明显。二维蜂窝结构的模拟结果也指出微结构的失稳是影响应变率效应的一个重要因素。

［1］Yang L M，Shim V.An analysis of stress uniformity in split Hopkinson bar test specimens［J］.International Journal of Impact Engineering，2005，31（2）：129－150.

［2］胡时胜，王悟，潘艺，等.泡沫材料的应变率效应［J］.爆炸与冲击，2003，23（1）：13－18.Hu Shi－sheng，Wang Wu，Pan Yi，et al.Strain rate effect on the properties foam materials［J］.Explosion and Shock Waves，2003，23（1）：13－18.

［3］王永胜，左孝青，尹志其，等.应变率对泡沫铝压缩性能的影响［J］.材料导报，2009，23（2）：47－52.Wang Yong－sheng，Zuo Xiao－qing，Yin Zhi－qi，et al.Effect of strain rate on compressive property of aluminum foam［J］.Materials Review，2009，23（2）：47－52.

［4］Lankford J，Dannemann K A.Strain rate effects in porous materials［C］∥Symposium Proceeding 521，Porous and Cellular Materials for Structure Applications.Warrendale：Materials Research Society，1998：103－108.

［5］Calladine C R，English R W.Strain－rate and inertia effects in the collapse of two types of energy－absorbingstructure［J］.International Journal of Mechanical Sciences，1984，26（11/12）：689－701.

［6］Tam L L，Calladine C R.Inertia and strain－rate effects in a simple plate－structure under impact loading［J］.International Journal of Impact Engineering，1991，11（3）：349－377.

［7］Zhao H，Abdennadher S.On the strength enhancement under impact loading of square tubes made from rate insensitive metal［J］.International Journal of Solids and Structures，2004，41（24/25）：6677－6697.

［8］Chen C，Lu T J，Fleck N A.Effect of imperfections on the yielding of two dimensional foams［J］.Journal of the Mechanics and Physics of Solids，1999，47（11）：2235－2272.

［9］Grenestedt J L.On interactions between imperfections in cellular solids［J］.Journal of Materials Science，2005，40（22）：5853－5857.

［10］Deshpande V S，Fleck N A.High strain rate compressive behaviour of aluminium alloy foams［J］.International Journal of Impact Engineering，2000，24（3）：277－298.

［11］McCullough K Y G，Fleck N A，Ashby M F.Uniaxial stress－strain behaviour of aluminium alloy foams［J］.Acta Materialia，1999，47（8）：2323－2330.

［12］Dong X L，Gao Z Y，Yu T X.Dynamic crushing of thin－walled spheres：An experimental study［J］.International Journal of Impact Engineering，2008，35（8）：717－726.

［13］Gibson L J，Ashby M F.Cellular solids：Structure and properties［M］.Cambridge：Cambridge University Press，1997：309－343.