泡沫金属在冲击载荷下的动态压缩行为＊

张 健，赵桂平，卢天健

（西安交通大学机械结构强度与振动国家重点实验室，陕西 西安710049）

泡沫金属在压缩荷载作用下，既能承受很大的变形又能保持相对恒定的应力水平，是理想的轻质吸能防护材料。实际应用中，这种防护材料覆盖在被保护结构的外表面，在受到冲击荷载时只能传递允许的脉冲强度到被保护结构上，同时在承受冲击荷载的时间内不会达到密实状态，保证被保护结构的安全服役。目前泡沫金属已经应用于航天着陆器、汽车防撞结构、军用汽车的防爆底板（防止地雷袭击），处置疑似爆炸物的防爆罐等领域。

然而，很多学者发现多孔材料在高速冲击下会表现出不同于静态时的力学性能，如S.L.Lopatnikov等［1］发现Fraunhofer泡沫铝以26 m/s的速度冲击刚性墙时几乎没有发生变形，而在76 m/s时出现了明显的波阵面。P.Tan等［2－3］发现对于大孔径和小孔径两种Hydro泡沫铝，冲击速度分别在42和108 m/s以下时，应力增强现象不是很明显，但是超过了这个临界速度，变形就会表现出明显的冲击特征。I.Elnasri等［4］发现在冲击速度55 m/s时，Alporas泡沫铝和镍空心球团在波阵面前后应力的跳跃与初始应力平台之比达60%，而Cymat泡沫铝和5056铝蜂窝没有明显的应力提升。R.P.Merrett等［5］报道了Alporas泡沫铝在承受冲击和爆炸载荷时的实验结果，其冲击速度超过60 m/s会观察到明显的波阵面，而塑胶炸药起爆所产生的脉冲没有使泡沫铝产生冲击变形模式。有些学者对多孔金属的动态压缩行为进行了数值模拟，如文献［1，6－7］使用了连续性模型，通过设定材料本构参数来考虑可压缩性。为了模拟多孔金属材料的非均匀分布，Y.D.Liu等［8］和G.W.Ma等［9］使用了2D Voronoi细观有限元模型，但由于模型和实际泡沫材料的孔型和分布的差异，很难得出定量的结论。在理论方面，研究者大多基于一维冲击波在泡沫材料中传播的理论为框架，如R.S.Reidg等［10］假定材料一维本构关系为完全刚塑性锁死模型（rigid－perfectly plastic－locking，RPPL），忽略了泡沫材料在冲击过程中的弹性变形阶段。S.L.Lopatnikov等［1，11－12］考虑了泡沫材料中弹性阶段的变形，发展了理想弹塑性锁死模型（elastic－perfectly plastic－rigid，EPPR）。J.J.Harrigan等［13］针对木材给出了一维弹性软化强化模型（elastic－softening－hardening，ESH）。

由于实验结果有很大的离散性，实验中也无法清楚观测到试件高速变形的过程，2D Voronoi模型又不能完全表现泡沫金属实际的孔型和分布，本文中基于微CT扫描影像信息，建立泡沫金属材料二维细观有限元模型，考虑不规则胞孔的不均匀分布，拟合孔壁材料的弹塑性本构参数。通过数值计算方法研究泡沫金属作为防护吸能材料的吸能机理，定量分析泡沫金属材料在动态压缩过程中弹塑性波的传播、惯性效应和从冲击端到静止端的应力传递变化特征。

1 泡沫金属的有限元模型

如图1所示，根据闭孔泡沫铝（图1（a））一个截面实际胞孔的形状和分布，基于微CT扫描图像，建立了泡沫金属材料二维细观有限元模型试件（图1（c））［14］，模型的相对密度ρ－分布如图1（b）所示，平均相对密度为0.3，最大值为0.34，分布在沿高度h＝8～10 mm处，最小值为0.25，分布在沿高度2～4 mm处。模型的平面尺寸为10 mm×10 mm，厚度0.02 mm（沿厚度方向一个单元），约束平面外自由度。模型采用8节点六面体单元，单元尺寸0.04 mm，总单元数量接近20 000。利用有限元软件ANSYS/LS－DYNA对泡沫金属的受压性能进行数值模拟，计算时模型夹在2个刚性平面之间，上刚性面静止，下刚性面以恒定速率对模型进行压缩加载，设定最大压缩量为8 mm时终止计算，用刚性面的法向反力计算模型的名义应力应变曲线。采用单面接触算法，考虑了孔壁间所有可能发生的接触。有限元模型与刚性面间的摩擦因数象征性取为0.01，模拟实验中充分润滑的状态。为了精确地考虑模型的实际质量和惯性效应的影响，在计算中均没有使用质量缩放。

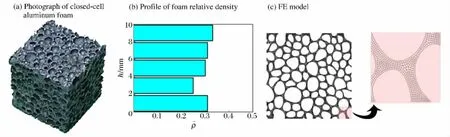
图1 泡沫金属材料二维细观有限元模型Fig.1 Two－dimensional mesoscale finite element models of metallic cellular materials

假定泡沫金属的基体材料为铝合金，密度2.7 g/cm3，本构模型选为程序内置的弹塑性模型［15］（＊MAT_PLASTIC_KINEMATIC），取弹性模量70 GPa，泊松比0.3，为了获取泡沫金属基体材料的本构参数，对泡沫铝试件（见图1（a））进行了准静态压缩实验，通过将二维细观有限元模型的准静态单轴压缩计算结果与实验结果的对比分析，可得基体材料本构参数中的屈服应力和强化模量分别为132.0和0.0 MPa，由此本构参数计算得到的泡沫金属名义应力应变曲线如图2所示。计算中未考虑材料的应变率效应。

此外，针对孔内气体的影响，作者采用流固耦合方法计算了孔内含气体的泡沫金属的动态压缩行为，结果表明，由于孔内气体和孔壁材料（金属）的刚度差别悬殊（相差4个数量级），孔内气体无法对孔壁的变形起到约束作用，也不能对泡沫金属的宏观力学性能产生可察觉到的影响，因此本文中忽略孔内气体的影响。

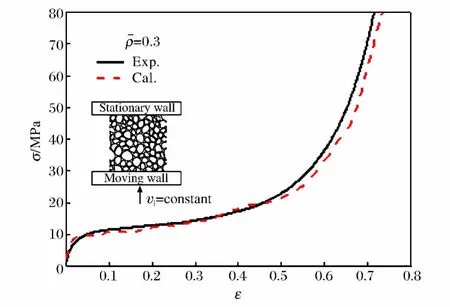
图2 泡沫金属单轴压缩的名义应力应变曲线Fig.2 Numerically predicted and experimentally measured uniaxial compressive stress versus strain curves for closed－cell aluminum foams

2 数值计算结果分析

通过计算，得到相对密度0.3的泡沫金属在不同速度下的压缩变形过程，如图3所示。从中可以看到2种截然不同的变形模式，准静态模式（图3（a））和动态模式（图3（b）～（c））。

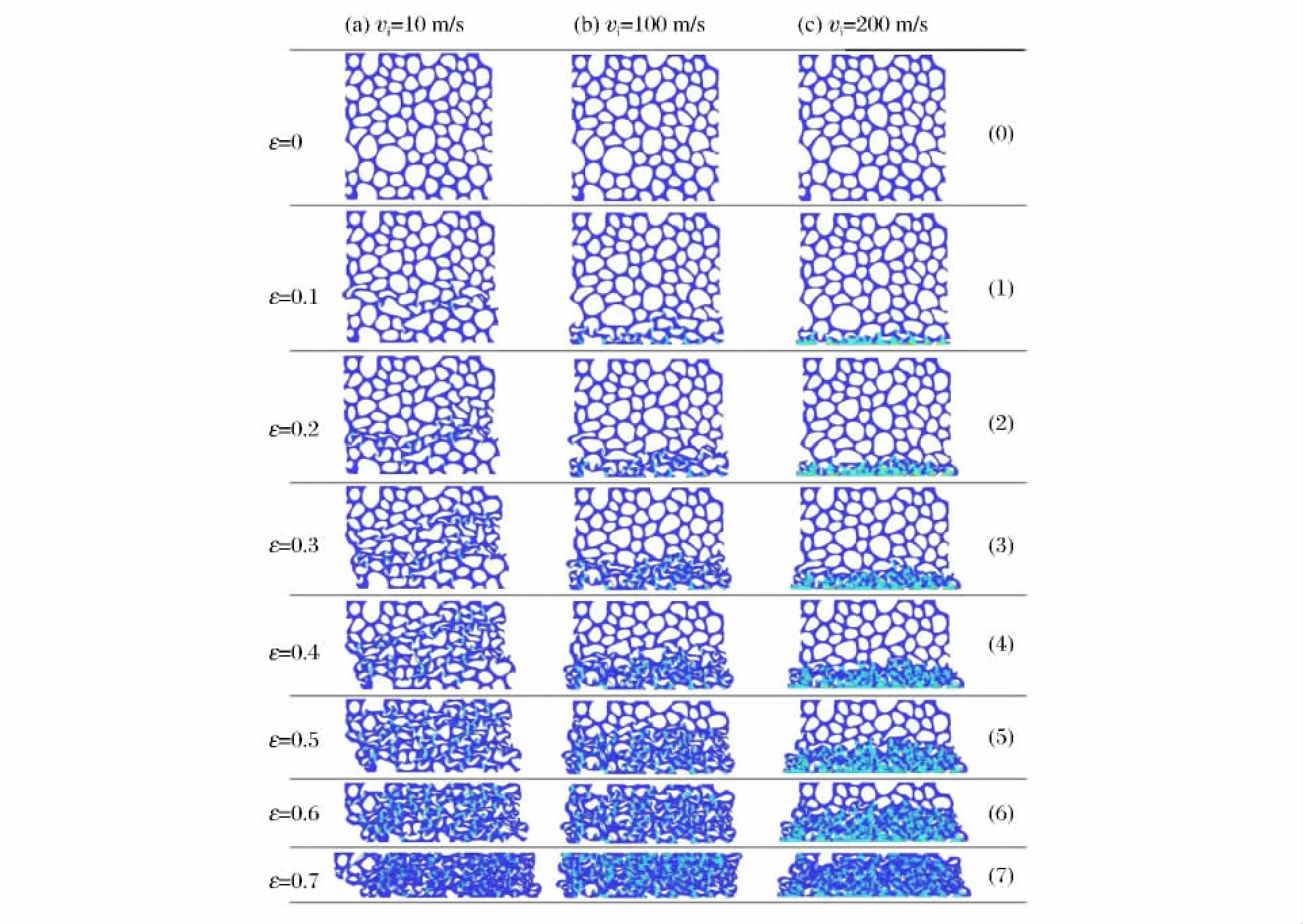
图3 泡沫金属在不同速度压缩下的变形图Fig.3 Simulated deformation modes of aluminum foam （relative density of 0.3）under different impact velocities

当加载速度为10 m/s时，泡沫金属的变形模式与准静态压缩相同，其塑性屈曲首先集中出现在大胞孔的孔壁中段，在图3（a）（1）中表现为可以继续承受荷载的塑性铰，这是由于泡沫金属的胞孔分布很不均匀，大胞孔孔壁的长细比最大，而孔壁中段部分截面又属于薄弱截面。图3（a）（1）中产生塑性铰的区域为一个不规则的变形带，宏观上主要集中在相对密度分布最小的区域，沿高度2～4 mm处（见图1（a））。随着压缩量的增大，变形带中胞孔孔壁间会发生接触，接触点相当于给薄弱孔壁提供了支撑，减少了薄弱孔壁的计算长度，其承载力便得到提高，这时又会有相对薄弱的孔壁出现塑性变形，形成另一个变形带。在此过程中，泡沫金属的应力应变曲线会形成一个近似恒定的应力平台，直到几乎所有的孔壁都发生接触（见图3（a）（6）），坍塌过程结束，试件变形整体上进入密实化阶段，这一阶段，孔壁间的接触面进一步增大，承载力进一步提高，试件发生明显的侧向变形，类似于不可压缩材料的塑性流动。

当加载速度为200 m/s时，泡沫金属的变形模式与准静态压缩时完全不同，试件在动态加载面附近首先出现孔壁坍塌（见图3（c）（1）），并且发生局部密实化现象，试件变形很不均匀，存在一个明显的波阵面把试件分为2个区域，即塑性变形区和弹性变形区。随着压缩量的增大，塑性变形区域向静止面扩展（见图3（c）（1）～（6）），这个过程就是塑性波在泡沫金属中传播的过程，直到压缩应变达到0.7左右，塑性波阵面到达静止面，弹性变形区才完全消失，但此时试件已基本上处于密实状态（见图3（c）（7））。

加载速度为100 m/s时泡沫金属也发生动态变形模式（见图3（b）），对比图3（c），我们发现，其波阵面界限不是特别清楚，塑性变形区的密实化程度较低，在应变0.6时达到密实化（见图3（b）（6）），密实化应变有所提前，此时的变形模式处于准静态向动态转换的过渡阶段。

泡沫金属用作防护结构时，人们主要关心传递到被保护结构上的荷载值，为了研究冲击载荷下泡沫金属的吸能削波作用，计算分析了不同加载速度时泡沫金属中静止面的应力－时间历程。图4给出了根据泡沫金属静止面反力得到的名义应力应变曲线。

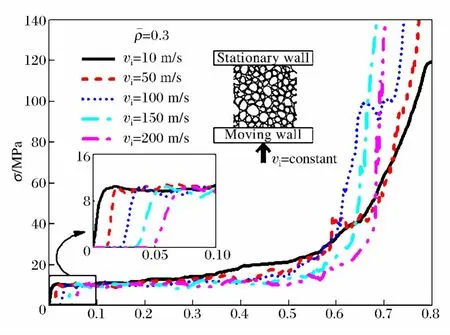
图4 泡沫金属动态压缩的名义应力应变曲线Fig.4 Numerically predicted uniaxial compressive stress versus strain curves for aluminum foams

可以看到，不同冲击速度下，应力应变曲线的起始点都存在一定的延时，冲击速度越大，起始点越推后，起始应变可以由下式计算：

式中：vi为刚性面的加载速度，ve为泡沫金属的弹性波速。

当加载速度为200 m/s时，直到名义应变达到0.04，静止面才开始出现应力，表明弹性波传到静止面，由公式（1）可以粗略地求出泡沫金属的弹性波速为5 km/s。取孔壁材料的密度为2.7 g/cm3，弹性模量为70 GPa，则根据公式求得孔壁材料的弹性波速为5.092 km/s，也就是说泡沫金属的弹性波与孔壁材料的弹性波速相当。其后是持续很短时间的一个振荡区，主要是冲击初始阶段泡沫金属中应力波的传播和在界面之间的来回反射形成的。接下来是一个很长的应力平台，直到名义应变达到0.6时，塑性波还没有传到静止面，应力平台是弹性变形的结果。名义应变0.6以后，塑性波逐渐到达静止面，应力平台开始上升，在名义应变0.7左右，塑性波阵面到达静止面，由于材料已接近密实，加上塑性变形区高速撞击静止面的惯性效应，使得应力应变曲线陡然上升。

当加载速度为10 m/s时，其名义应力应变曲线和准静态加载的应力应变曲线相同，总体可以分为3部分：弹性段，平台（坍塌）段和密实段。

有趣的是，当加载速度为100 m/s时，其名义应力应变曲线会产生第2个应力平台。下面结合其变形图3（b）分析原因，从图4看出，静止面应力起始于名义应变0.02时，正好等于加载速度200 m/s时的一半，这时弹性波到达静止端面；当名义应变0.1时，试件产生的塑性铰明显多于加载速度10 m/s的情况（见图3（b）（1）），而且主要集中在动态加载端，并非是在试件材料分布相对薄弱的2～4 mm段；名义应变0.5时，塑性波逐渐到达静止面，应力开始提高，名义应变0.6时，塑性波阵面到达静止面（见图3（b）（6）），加上塑性变形区撞击静止面的惯性效应，应力出现了强化。事实上，这时试件并未完全密实，在动态面继续压缩的过程中，没有完全密实的泡沫金属（图3（b）（6））又会重复图3（b）（1）～（6）的变形过程，试件进一步密实，静止面的应力又会表现出一个近似的平台和随后的强化。

从图4中可以发现，由于速度较低，加载速度为50 m/s时泡沫金属出现第2个应力平台比较低，但同样是通过二次压缩的过程才达到密实状态。而对于加载速度为150和200 m/s的泡沫金属，在第1次压缩后已经相当密实了，二次压缩现象不是很明显。

3 理论分析

为了分析在冲击载荷作用下泡沫金属中应力波的传播规律，下面引入经典的一维应力波理论［16］。

泡沫金属在高速加载时的冲击波传播过程如图5（a）所示，介质中描述波阵面前后的密度、应力和质点速度分别为：

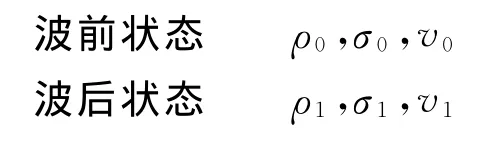
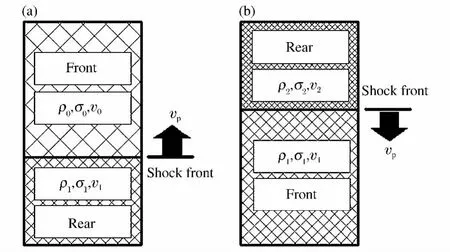
图5 冲击波传播示意图Fig.5 Schematic diagram of shock wave propagation in metallic cellular materials

假设闭孔泡沫金属在变形过程中质点的位移是连续的，根据质点运动的连续性条件，塑性波波阵面前后状态应满足：

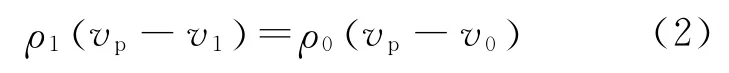
根据塑性波波阵面前后动量守恒条件可得到：

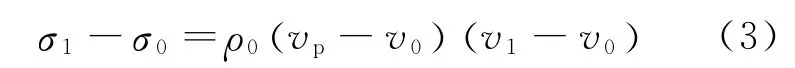
泡沫金属在动态压缩时波前与波后的物理状态参量可表示为：

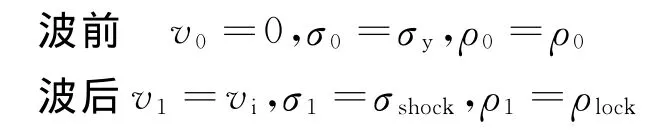
由公式（2）可以得到锁死密度

其中，定义动态锁死应变

通过数值模拟分析，发现泡沫金属的动态锁死应变εlock是变化的，与准静态加载下的密实应变εD有着本质的不同。直观上，从图3（b）～（c）可以看到，冲击速度越大，泡沫金属所能达到的动态锁死应变越大，塑性区越密实，材料的锁死密度ρlock也越大。动态锁死应变与冲击速度、塑性波速相关，问题的复杂性在于泡沫金属并不是理想的弹塑性材料，其塑性波速不是恒定的。动态锁死应变εlock在图4中表现为应力增强时的名义应变值，在加载速度为100、150和200 m/s时的动态锁死应变εlock分别为0.6、0.64和0.68，此处根据公式（5）可以反算出泡沫金属材料的塑性波速。表1中为泡沫金属高速冲击加载时数值计算结果，可见，随着加载速度的增大，泡沫金属的塑性波速会提高，锁死应变和锁死密度也会增大。

表1 泡沫金属高速冲击加载计算结果Table 1 Summary of FE predictions for aluminum foam （relative density of 0.3）under impact loading

由公式（3）可得到冲击应力

可以看到，泡沫金属在动态压缩时，加载面的应力由静态应力项和动态冲击项2部分构成，其中静态应力项为泡沫金属屈服应力，动态冲击项由材料密度、动态锁死应变及冲击加载速度决定，称为材料受到动态载荷作用时的惯性效应。泡沫金属在承受高速冲击时，由于惯性效应导致加载面产生应力的提升可以提高泡沫金属的吸能，在防护应用中起到有益作用。

注意到冲击应力σshock为动态加载面产生的应力，并非图4在加载速度为100 m/s时静止面表现出的达到动态锁死应变后的平台应力。 由上节的分析可知，该平台应力是由于泡沫金属的二次压缩产生的。

如图5（b）所示，塑性波传播到静止面发生反射，反射后泡沫金属发生二次压缩过程，这时，波前与波后的物理状态参量可表示为：

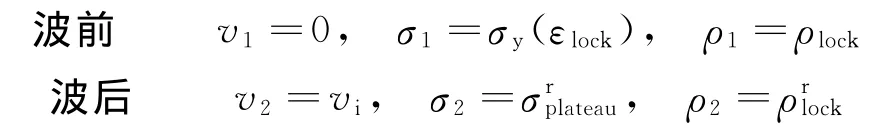
同样，根据波阵面前后动量守恒条件可得到

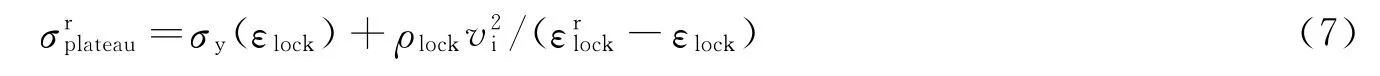
式中：σy（εlock）、ρlock和εlock分别为第1次压缩的屈服应力、锁死密度和锁死应变，εrlock为二次压缩的锁死应变。可以发现，和公式（6）类似，二次压缩时静止面的应力同样由静态应力项和动态冲击项2部分构成。受惯性作用的影响，二次压缩的应力平台也随着加载速度的增大而提高。

加载速度为100 m/s时，泡沫金属的二次压缩锁死应变根据图4取为0.725，第1次压缩的屈服应力、锁死密度和锁死应变从表1取值，代入公式（7）可以得到静止面的第2个平台应力为99.3 MPa，与图4中数值模拟计算结果基本相符。泡沫金属用作防护结构时，人们主要关心传递到被保护结构上的荷载值，即文中静止面上的应力大小。本文结果表明，当加载速度较大时，在静止端会产生二次应力，且二次应力远大于泡沫金属的屈服应力，从而有可能对静止面（被保护结构）造成伤害。在后续研究中，作者将结合被保护结构，系统研究在静止端产生的二次应力的影响。

4 结 论

通过数值模拟和理论分析，研究了泡沫金属在不同加载速度时的压缩变形机理，重点分析了弹塑性波的传播、惯性效应和从冲击加载端传递到静止端的应力变化特征。根据数值模拟结果，对于相对密度为0.3的泡沫铝，弹性波速约为5 km/s，与孔壁材料的弹性波速相当，塑性波速在83～294 m/s间变化，表现为随着加载速度的增大而增大。在加载速度为50～100 m/s间变形模式从准静态模式转变为动态模式，未发现明显的临界速度。泡沫金属在高速压缩时，静止端主要承受屈服应力（近似为平台应力），动态锁死应变随着加载速度的增大而增大。由于塑性波发生反射，试件会发生二次压缩过程，相应地，静止端产生的二次应力平台。受惯性作用的影响，二次压缩应力平台也随着加载速度的增大而提高。采用泡沫金属作为防护材料时，除了考虑利用第1次压缩过程吸收能量，还须防止在静止端产生的二次应力对被保护结构造成伤害。

［1］Lopatnikov S L，Gama B A，Haque M J，et al.Dynamics of metal foam deformation during Taylor cylinder－Hopkinson bar impact experiment［J］.Composite Structures，2003，61（1/2）：61－71.

［2］Tan P，Harrigan J，Reid S.Inertia effects in uniaxial dynamic compression of a closed cell aluminium alloy foam［J］.Materials Science and Technology，2002，8：480－488.

［3］Tan P J，Reid S R，Harrigan J J，et al.Dynamic compressive strength properties of aluminium foams.Part I－Experimental data and observations［J］.Journal of the Mechanics and Physics of Solids，2005，53（10）：2174－2205.

［4］Elnasri I，Pattofatto S，Zhao H，et al.Shock enhancement of cellular structures under impact loading：PartⅠ－Experiments［J］.Journal of the Mechanics and Physics of Solids，2007，55（12）：2652－2671.

［5］Merrett R P，Langdon G S，Theobald M D.The blast and impact loading of aluminium foam［J］.Materials ＆Design，2013，44：311－319.

［6］Pattofatto S，Elnasri I，Zhao H，et al.Shock enhancement of cellular structures under impact loading：PartⅡ－Analysis［J］.Journal of the Mechanics and Physics of Solids，2007，55（12）：2672－2686.

［7］Karagiozova D，Langdon G S，Nurick G N.Propagation of compaction waves in metal foams exhibiting strain hardening［J］.International Journal of Solids and Structures，2012，49（19/20）：2763－2777.

［8］Liu Y D，Yu J L，Zheng Z J，et al.A numerical study on the rate sensitivity of cellular metals［J］.International Journal of Solids and Structures，2009，46：3988－3998.

［9］Ma G W，Ye Z Q，Shao Z S.Modeling loading rate effect on crushing stress of metallic cellular materials［J］.International Journal of Impact Engineering，2009，36：775－782.

［10］Reid S R，Peng C.Dynamic uniaxial crushing of wood［J］.International Journal of Impact Engineering，1997，19（5/6）：531－570.

［11］Lopatnikov S L，Gama B A，Gillespie J W.Modeling the progressive collapse behavior of metal foams［J］.International Journal of Impact Engineering，2007，34（3）：587－595.

［12］Lopatnikov S L，Gama B A，Haque M J，et al.High－velocity plate impact of metal foams［J］.International Journal of Impact Engineering，2004，30（4）：421－445.

［13］Harrigan J J，Reid S R，Tan P J，et al.High rate crushing of wood along the grain［J］.International Journal of Mechanical Sciences，2005，47（4/5）：521－544.

［14］张健，赵桂平，卢天健.闭孔泡沫铝应变率效应的试验和有限元分析［J］.西安交通大学学报，2010，44（5）：97－101.Zhang Jian，Zhao Gui－ping，Lu Tian－jian.Experimental and numerical study on strain rate effects of close－celled aluminum foams［J］.Journal of Xi’an Jiaotong University，2010，44（5）：97－101.

［15］Hallquist J O.LSTC LS－DYNA user’s manual［Z］.Livermore，CA，US：Livermore Software Technology Corporation，2007.

［16］Wang Li－li.Foundation of stress waves［M］.Beijing：National Defense Industry Press，2005.