混凝土材料动态本构参数的分阶段计算反求技术＊

陈 睿，刘 杰，韩 旭，毕仁贵

（1.湖南大学汽车车身先进设计制造国家重点实验室，湖南 长沙410082；2.湖南大学机械与运载工程学院，湖南 长沙410082）

混凝土材料广泛应用于防撞击和防爆结构、机场跑道和核电站等民用和军用设施，因此研究混凝土材料的动态力学性能具有十分重要的理论意义和现实指导作用。混凝土是一种复合材料，主要由水泥砂浆、骨料及黏结层组成。由于水泥砂浆和骨料的物理、力学性能差异明显，骨料的形状不规则和分布的不确定，以及含有大量不规则的初始裂纹和气泡等因素，导致了混凝土材料的动态力学性能十分复杂。近几十年来，学者们对混凝土材料的动态力学性能进行了广泛的研究［1－3］，构建了许多关于混凝土材料的动态本构模型，常用的有 HJC模型［4］、RHT 模型［5］及 TCK 模型［6］等。

材料本构模型都含有很多参数，这些参数中大多数可以通过物理和力学实验进行确定，但有些参数不能通过实验直接获取，常常需要大量不同的实验数据，通过拟合来确定。然而对混凝土材料而言，由于混凝土试样制备的困难和实验设备的限制，要获得大量有效的实验数据是相当耗时费力的。因此，寻求其他快捷途径来确定这些难以确定的参数是十分必要的。近些年来，基于材料的动态响应来反求材料特性取得了一定的进展［7－11］。这类参数反求方法中，材料的动力响应与材料参数之间的复杂关系一般由正问题的计算模型来表示。材料参数的反求是通过反复调整正问题计算模型中的材料参数，使得计算模拟响应与测量响应之间的误差最小，最终获得与测量响应吻合最好的材料参数。

通常，这类参数反求方法都是基于所有实验测量响应数据反求出所有与测量响应具有一定敏感性的参数。这样虽然能够确定这些参数的取值，但由于未知参数对不同类型实验测量响应的敏感性差异以及不同类型实验测量响应的量级不同，会导致在一定程度上缺乏对实验测量响应数据的综合利用，并影响参数反求的精度。为了充分利用实验测量响应信息，本文中提出了一种分阶段参数计算反求技术以获取混凝土HJC本构模型中的关键参数。结合不同应变率下的混凝土SHPB实验，基于参数敏感性分析及分类，将透射波和反射波响应作为输入信息，分阶段反求出混凝土HJC本构参数，并将确定参数后的计算结果与实验结果进行对比分析。

1 HJC动态本构模型及其参数

混凝土HJC本构模型［4］是一种综合考虑大应变、高应变率及高压效应的混凝土计算本构模型。该模型考虑了材料损伤、应变率效应以及静水压力对屈服应力的影响，主要包括3方面：等效强度模型、损伤模型和状态方程。其中等效强度模型为：

式中：σ＊＝σ/fc，P＊＝P/fc和分别表示归一化的等效强度、归一化压力和量纲一应变率。其中σ、P和分别为实际的等效强度，压力和应变率，fc为准静态单轴抗压强度，为参考应变率。A、B、N、C是材料的强度模型参数，分别表示材料内聚强度、压力硬化系数、压力硬化指数、应变率硬化系数。D 为损伤因子（0≤D≤1.0），并引入一个最大量纲一强度Smax，σ＊≤Smax。

混凝土HJC动态本构模型［4］共含有20个参数，可以通过不同的途径来确定。其中，可以直接通过简单的物理或力学实验获取4个参数，即初始密度ρ0、弹性模量E、拉伸强度T和fc；可以间接通过实验或经典的计算公式［4］确定6个参数，即2个损伤参数（D2，εf，min）和4个压力参数（弹性体积模量K、弹性极限静水压力Pcrush及对应的体应变μcrush、压实体应变μlock）；而其他10个参数（5个强度参数A、B、N、C、Smax，1个损伤参数D1和4个压力参数（压实静水压力Plock、K1、K2、K3））需要通过大量有效的实验数据进行拟合来确定。然而要获取大量有效的实验数据成本较高，且费时耗力，想要快速获取这些参数是较为困难的。因此本文中将采用分阶段计算反求技术来快速获取这些较难确定的参数。

2 混凝土本构参数反求

2.1 分阶段计算反求技术

在利用计算反求技术进行参数确定过程中，通常都是基于所有实验测量响应数据来同时反求所有的未知参数。这往往会由于未知参数对实验测量响应的敏感程度不同，测量响应数据与未知参数类型不匹配，不同类型实验测量响应数据量级水平不同等问题，使得在一定程度上缺乏对测量响应数据的综合利用，并导致反求结果不够理想。为此，本文中提出了一种分阶段参数反求技术，该方法基于多种不同的实验，将参数反求问题进行细化，对未知参数进行敏感性分析及分类，并在此基础上分阶段反求出各类参数，且每一次参数反求均利用前一次反求结果作为基础，该参数反求方法的流程如图1所示。

图1 分阶段参数反求流程图Fig.1 Flow chart of the multi－stage inverse technique for parameters identification

分阶段参数反求方法中最明显的特点在于基于不同实验建立的正问题，对所有未知参数进行敏感性分析，根据各参数的敏感性高低程度，将这些未知参数划分为几类（每类对应1组实验）。在进行分阶段参数反求时，首先对敏感性程度最高的一类参数，结合相应的实验，利用反求方法确定这类参数。确定之后采用同样的方法进行其他类参数反求，在每一次参数反求时都将上一次反求的结果作为当前参数反求的已知条件。这样分阶段地对各类参数进行反求，最后获得所有参数的取值。在本文中每阶段参数反求过程中，采用遗传算法［12］作为反问题的求解器，该算法的最大优势在于其具有较强的全局最优搜索能力和较快的全局收敛速度，能够克服局部最优，并在全局范围内寻找到最优解。

本文中将利用该分阶段参数反求方法，结合不同应变率下的混凝土SHPB实验，对混凝土HJC本构中关键参数进行反求。该SHPB实验数据来源于文献［3］对混凝土试样进行3种不同应变率（case 1：17 s－1；case 2：25 s－1；case 3：200 s－1）加载的实验。文献［3］给出了较为详细的SHPB实验装置的几何尺寸和混凝土试件的基本材料参数，以及测试得到的响应曲线。

2.2 正问题的建立

基于文献［3］中SHPB实验装置，建立相对应的有限元模型。由于撞击杆、输入杆、输出杆和试件的几何尺寸都是轴对称的，同时为了提高计算效率，采用PLANE162平面轴对称单元建立二维轴对称有限元模型，如图2所示。撞击杆、压杆和试件在径向分别划分15、15、30个单元，轴向分别划分740、2 300、60个单元。在数值计算中，采用LS－DYNA软件作为正问题的求解器，且两两接触采用单面自动接触算法。

图2 SHPB的二维轴对称有限元模型Fig.2 2D axisymmetric finite element model for the SHPB experiment

撞击杆、输入杆和输出杆均为相同的弹性材料，因此都采用线弹性材料模型，材料参数为：密度7.83 g/cm3、弹性模量200 GPa、泊松比0.3。混凝土试件采用 HJC动态本构模型，其中ρ0、E、T 和fc等基本参数源自文献［3］，材料的压实密度ρgrain和Plock源自文献［13］。鉴于第1节中所述，结合文献［4］中的计算公式可获取K、Pcrush、μcrush、μplock和μlock。由于在SHPB实验的应变率范围内混凝土的压力仅能达到过渡段，使得状态方程中压实段的参数对数值计算结果影响较小［14］，因此该段方程的参数K1、K2和K3取原始文献［4］的数值。另外，数值研究发现最大量纲一强度参数和损伤参数的变化对该问题的计算结果影响较小，因此本文中Smax、D1和D2也取原始文献［4］中的数值。因此，除了强度参数A、B、C、N 外，混凝土HJC模型的其他参数如表1所示。

表1 混凝土HJC本构模型的基本参数Table 1 The material parameters for HJC concrete constitutive model

2.3 参数敏感性分析及分类

利用计算反求技术进行参数反求时，要求反求的参数必须对输出的响应具有较强的敏感性。分别基于低应变率和高应变率的SHPB实验，对强度参数A、B、C、N进行敏感性分析。基于低应变率工况（case 1）对这4个参数进行敏感性分析，结果如图3所示。从图3中可以发现，参数A、B、N 取不同值时，计算响应结果（反射波和透射波）变化很大，而参数C取值的变化对计算响应结果几乎没有影响。这说明在低应变率工况下，参数A、B、N 具有较高的敏感性，而参数C的敏感性较低。同样基于高应变率工况（case 3）下对4个参数进行敏感性分析，发现计算响应结果随着这4个参数取值的变化而变化，其中参数C的敏感性分析结果如图4所示。这说明在高应变率工况下，4个参数都具有较高的敏感性，尤其参数C的敏感性很高。参数C表示应变率参数，且从公式（1）中可以看出应变率对强度的影响表现为应变率的对数，这就可以发现当处于低应变率时，（1＋C lnε′＊）的值几乎在1.0左右；而当在高应变率ε·≥102s－1时，由于量级的影响，使得参数C的变化对（1＋C lnε′＊）的影响很大，这进一步说明在高应变率下，参数C具有较强的敏感性。

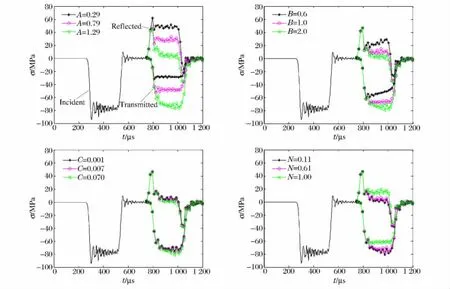
图3 基于工况1对参数A、B、C、N 敏感性分析Fig.3 Sensitivity analysis for parameters A，B，C，N based on case 1

图4 基于工况3对参数C敏感性分析Fig.4 Sensitivity analysis for parameter C based on case 3

基于上述敏感性分析及各参数的敏感性程度，将4个强度参数分为2类，即第1类包含3个参数A、B、N，这一类参数将基于低应变率工况的实验进行参数反求。第2类为参数C，这类参数将基于高应变率工况实验进行参数确定，在反求过程中，将第1类参数反求的结果作为已知条件。

2.4 结果及验证

结合实验测量的响应及参数敏感性分析，可以初步确定参数的取值范围，即A∈［0.2，1.0］，B∈［0.4，1.5］，N∈［0.5，1.2］，C∈［0.05，0.2］，且在反求时这4个参数的初始值都设为取值范围的平均值。在敏感变化的透射波和反射波响应790～1 100μs区域中采样24个时刻的离散点以构造优化目标函数：

基于低应变率case 1实验，利用上述的反求方法确定第1类参数A、B和N，计算反求结果如表2所示。

表2 分阶段参数反求的结果Table 2 The inversed results by multi－stage inverse technique

为了验证反求参数的适用性，分别将反求得到的参数代入正问题，在2种低应变率工况（case 1和case 2）下进行数值计算，并将计算结果与实验数据进行对比。其中case 2实验没有参与参数反求，而作为反求参数适用性的验证。图5～6分别给出了2种低应变率下的计算结果，从图中可以看出，2种应变率下的计算结果与实验曲线较为吻合。

基于上述第1类参数反求的结果，结合较高应变率下的实验数据，再利用反求技术确定第2类参数C的值，反求结果如表3所示。将得到的参数C值代入正问题计算，其结果如图7所示。从图中可以看出，数值计算的结果与实验测量数据较为吻合。这说明基于本文分阶段计算反求技术进行参数确定是可行的，所得到的结果较为准确。

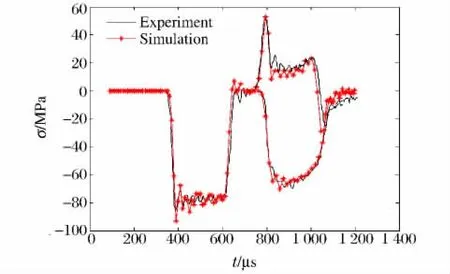
图5 工况1的计算结果与实验结果比较Fig.5 The computational results for case 1 compared with experimental data

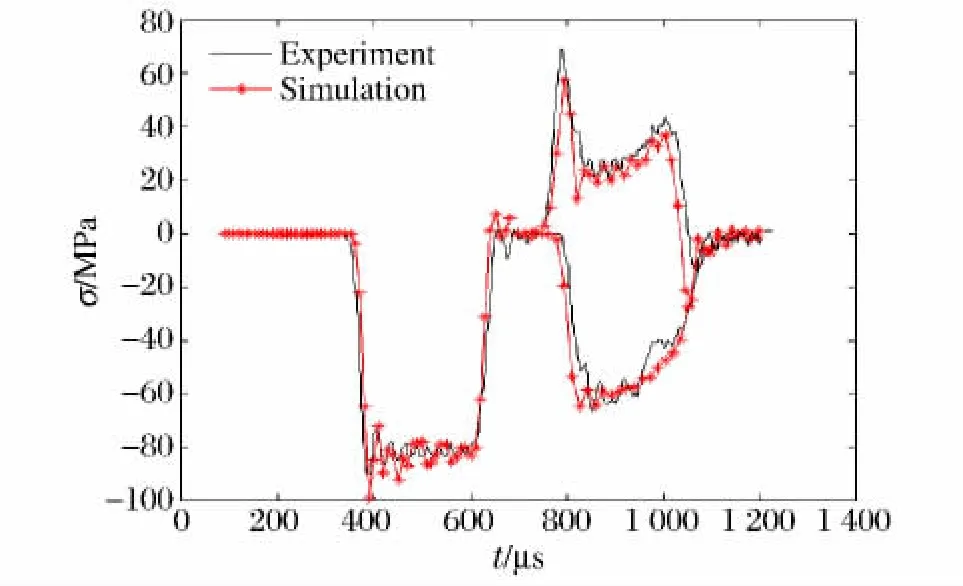
图6 工况2的计算结果与实验结果比较Fig.6 The computational results for case 2 compared with experimental data

图7 工况3的计算结果与实验结果比较Fig.7 The computational results for case 3 compared with experimental data

3 结 论

提出了一种分阶段的计算反求技术以确定混凝土本构模型中的关键参数。在该方法中，基于2种不同应变率下的SHPB实验，对未知参数进行敏感性分析及分类，在此基础上分阶段反求各类参数，且每次参数反求时均利用上一次反求结果作为基础，从而分阶段确定了混凝土本构参数。本文中每阶段的参数反求都是根据透射波和反射波响应反求材料本构参数，这样避免了应力波效应和应变率效应解耦问题，不必分离结构响应和材料响应。参数反求结果表明，该分阶段计算反求方法充分利用不同的实验响应，能较为快速、稳定地确定一些传统方法较难以确定的参数。该计算反求方法充分结合实验与数值计算，通过实验响应确定参数，减少实验次数，提高效率，在工程实际中具有重要意义。

［1］Ross C A，Thompson P Y，Tedesco J W.Split－Hopkinson pressure－bar tests on concrete and mortar in tension and compression［J］.ACI Materials Journal，1989，86（5）：475－481.

［2］Bischoff P H，Perry S H.Compressive behaviour of concrete at high strain rates［J］.Materials and Structures，1991，24（6）：425－450.

［3］Tedesco J W，Hughes M L，Ross C A.Numerical simulation of high strain rate concrete compression tests［J］.Computers ＆ Structures，1994，51（1）：65－77.

［4］Holmquist T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjected to large strains，high strain rates，and high pressures［C］∥Jackson N.Proceedings of the 14th International Symposium on Ballistics.USA：American Defense Preparedness Association，1993：591－600.

［5］Riedel W，Thoma K，Hiermaier S，et al.Penetration of reinforced concrete by BETA－B－500 numerical analysis using a new macroscopic concrete model for hydrocodes［C］∥Proceedings of the 9th International Symposium on Interaction of the Effects of Munitions with Structures.Berlin，Germany，1999：315－322.

［6］Taylor L M，Chen E P，Kuszmaul J S.Microcrack－induced damage accumulation in brittle rock under dynamic loading［J］.Computer Methods in Applied Mechanics and Engineering，1986，55（3）：301－320.

［7］Han X，Liu G R.Computational inverse technique for material characterization of functionally graded materials［J］.American Institute of Aeronautics and Astronautics，2003，41（2）：288－295.

［8］Cooreman S，Lecompte D，Sol H，et al.Elasto－plastic material parameter identification by inverse methods：Calculation of the sensitivity matrix［J］.International Journal of Solids and Structures，2007，44（13）：4329－4341.

［9］Sedighi M，Khandaei M，Shokrollahi K H.An approach in parametric identification of high strain rate constitutive model using Hopkinson pressure bar test results［J］.Materials Science and Engineering：A，2010，527（15）：3521－3528.

［10］伍乾坤，韩旭，胡德安.一种陶瓷脆性材料动态本构参数的计算反求方法［J］.固体力学学报，2009，30（3）：280－285.Wu Qian－kun，Han Xu，Hu De－an.An inverse technique for identification of dynamic constitutive parameters of ceramic brittle material［J］.Acta Mechanica Solida Sinica，2009，30（3）：280－285.

［11］Chen R，Han X，Liu J，et al.A computational inverse technique to determine the dynamic constitutive model parameters of concrete［J］.Computers Materials ＆ Continua，2011，25（2）：135－157.

［12］Liu G R，Han X.Computational inverse techniques in nondestructive evaluation［M］.Boca Raton：CRC Press，2003.

［13］Hao Y F，Hao H，Li Z X.Numerical analysis of lateral inertial confinement effects on impact test of concrete compressive material properties［J］.International Journal of Protective Structures，2010，1（1）：145－167.

［14］巫绪涛，李耀，李和平.混凝土 HJC本构模型参数的研究［J］.应用力学学报，2010，27（2）：340－344.Wu Xu－tao，Li Yao，Li He－ping.Research on the material constants of the HJC dynamic constitutive model for concrete［J］.Chinese Journal of Applied Mechanics，2010，27（2）：340－344.