隧道爆破近区振动的预测方法＊

张在晨，林从谋，黄志波，葛冰洋，徐 亮

（华侨大学岩土工程研究所，福建 厦门361021）

近年来，随着经济建设的发展，越来越多的现有公路隧道已不能满足日益增长的交通需求。在高速公路扩建工程中，考虑到路线走廊带是不可再生的资源，且由于特殊的地质和地形条件、桥隧衔接方式、总体线路线型和工程造价等因素的限制，扩建隧道与既有隧道的净间距已不能满足设计规范中对分离式隧道间距的要求，从而衍生出小净距隧道这一结构形式。因小净距隧道空间结构较为特殊，钻爆施工易在围岩中产生较大的冲击荷载，对围岩造成损伤［1］。因此，控制爆破振动对保证围岩稳定性显得尤为重要。目前主要以爆破远区的振动规律［2－3］来评估爆破施工对近区围岩稳定性的影响。然而，利用爆破远区振动规律预测爆破近区振动，其偏差值较大［4－5］。由于爆破近区的复杂性，应力应变场在短时间内发生了剧烈变化，导致其难以测量［6］等困难，至今仍未对隧道爆破近区振动进行深入研究。

为了研究隧道爆破近区的振动规律，应先对其进行合理的分区。逄焕东等［7］借助解析和数值计算相结合的方法，研究弹性介质中爆破地震波传播的分区变化规律及不同区域的频率特点；陈士海等［8］在某小区地基爆破开挖工程中，采用比例距离对爆破振动的近、中、远区进行划分，并研究爆破地震波沿各分区信号的频谱及能量分布特征。然而，目前尚未提出较为合理的隧道爆破振动分区方法。

为解决上述问题，本文中将比例距离的概念应用于隧道爆破振动的分区之中，提出较为合理的量化分区方法。在此基础上，首次提出采用BP小波神经网络模型预测隧道爆破近区振速的新方法，将BP小波神经网络应用于新建分离式隧道和复杂环境下的小净距隧道钻爆施工控制中，并与经验公式所得的预测值进行对比，验证预测模型的可行性。

1 隧道爆破振动分区

在半无限介质内的球形装药引爆后，其质点位移解一般可表示为：

式中：A、B为权重参数，取决于岩体、地质条件及波的传播时间；R为爆源距。由式（1）可知，在R较小时，质点位移主要由第1项决定；在R较大时，质点位移主要由第2项决定。因A、B权重值一般难以获取，且为便于与不同规模的爆破进行比较，将实际距离转化为比例距离进行处理［7］。将萨道夫斯基经验公式所描述的介质质点振速、药量和爆源距三者的关系变形如下：

式中：v为介质质点振动速度幅值，cm/s；R为爆源距，m；Q为产生爆破振动的相应炸药量，kg；K、α是与爆破点至介质质点间的地质条件有关的系数和衰减指数；为比例距离，。

对式（2）两边求导，则可得：

根据装药量和爆源距确定测点离震源的比例距离，绘制其速度衰减曲线以确定其属于爆破近区、中区或远区。综合不同情况爆破分区［7－8］的依据，本文中提出以速度衰减曲线的斜率k′的大小作为判别隧道爆破近、中、远区的标准，即：

（1）当k′＜－5时，爆破振动速度衰减速度快，对应于爆破振动近区；

（2）当－5≤k′≤－1时，爆破振动速度衰减速度逐渐变慢，对应于爆破振动中区；

（3）当k′＞－1时，爆破振动速度衰减速度缓慢，对应于爆破振动远区。

在无实测值时，K、α可参考爆破安全规程［9］选取。则依据速度衰减曲线斜率k′大小，隧道爆破振动分区可大致划分为：为近区；为中区；为远区。若有实测值，则应绘出速度衰减曲线后，以速度衰减曲线的斜率k′的大小划分隧道爆破近、中、远区。

2 隧道爆破近区预测方法

由于爆破近区的复杂性，应力应变场在短时间内发生了剧烈的变化而难以获取，且对于隧道爆破而言，爆破近区的监测环境极为恶劣，因此研究仍未深入。本文中结合棋盘山隧道（双洞分离式隧道）的监测数据，采用BP小波神经网络方法预测爆破近区振速，并对方法的可行性进行验证。

2.1 BP小波神经网络理论

小波神经网络（WNN）是以小波元代替神经元，通过作为一致逼近的小波分解建立的小波变换与神经网络结合。在输入信号序列为xi（i＝1，2，…，k）时，隐含层输出计算公式为：

式中：h（j）为隐含层第j个节点的输出值，hj为小波基函数；wij为输出层和隐含层的连接权值；bj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子。

在爆破振动速度衰减规律的研究中，隐含层的激励函数采用Morlet小波基函数，其计算公式为：

输出层选用Sigmoid函数，其计算公式为：

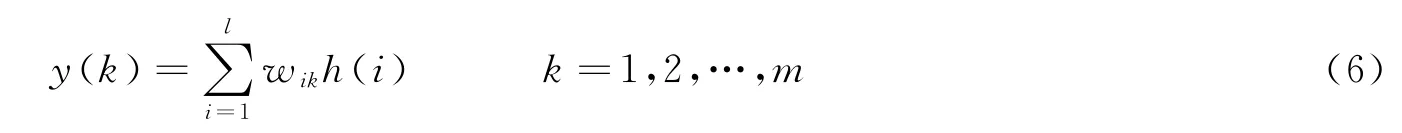
2.2 隧道爆破近区预测模型及步骤

基于MATLAB2009a建立隧道爆破近区预测模型，其主要训练步骤如下：

步骤1：网络参数初始化。确定输入节点个数M＝2，输出节点个数N＝1，神经元个数n＝6，训练误差egoal＝0.001，动量因子μ＝0，学习率lr1＝lr2＝0.01。将小波的伸缩因子aj、平移因子bj以及网络权值wij、wjk随机赋予初始值。

步骤2：预测输入。将训练样本输入网络，计算网络预测输入并计算网络输出和期望输出的误差E。如果误差函数E 变大，则ηi＝lηi－1（取l＝0.2），否则ηi＝gηi－1（取g＝1.15）。

步骤3：权值修正。根据误差E修正网络权值和小波函数的相关参数，使网络预测值逼近期望值，重复直至算法结束。

2.3 模型可行性验证

为验证隧道爆破近区预测模型的适用性，将其应用于棋盘山隧道中导洞掌子面围岩爆破振动预测中。依据第1节提出的隧道爆破振动分区方法，可将棋盘山隧道中导洞掌子面围岩爆破振动划分为：比例距离在0～5.05范围内为近区；比例距离在5.05～8.64范围内为中区；比例距离大于8.64为远区。以文献［10］中爆破远区的监测数据作为学习样本进行训练，对中导洞掌子面围岩爆破近区振速［4］进行预测，其预测结果如表1所示。

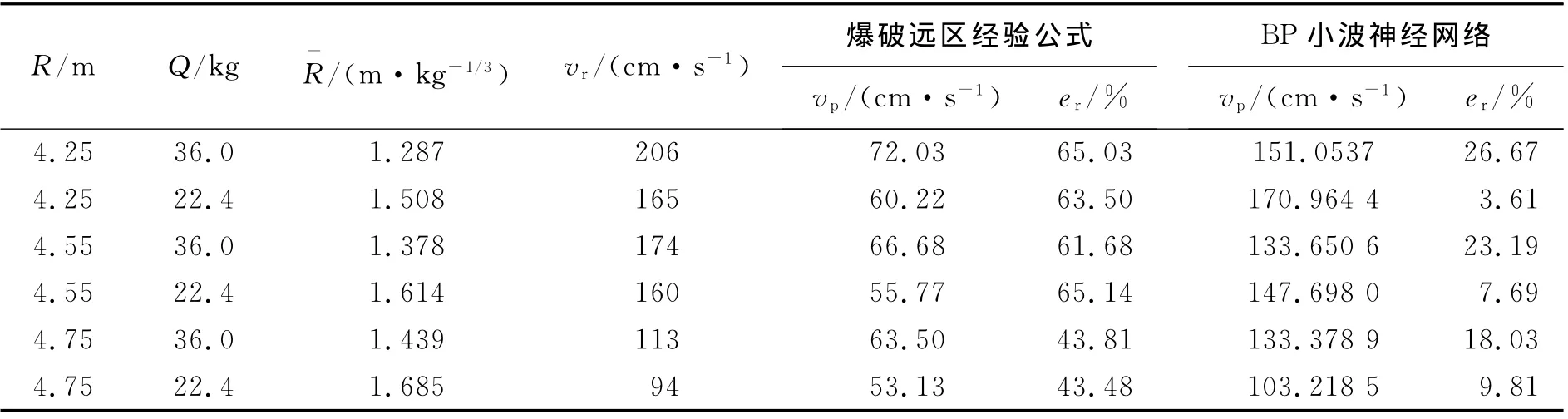
表1 中导洞掌子面围岩实测振速与预测振速对比Table 1 Comparison of blasting vibration velocities between site monitor and prediction of surrounding rock of tunnel face

由表1可知，采用爆破远区经验公式预测近区掌子面振速，其误差波动范围为43.48%～65.14%，平均相对误差为57.11%；采用BP小波神经网络模型预测，误差波动范围为3.61%～26.67%，平均相对误差为14.83%。可见，采用BP小波神经网络模型，以爆破远区数据作为训练样本，对近区爆破振速进行预测，能获得精度较经验公式高的预测值。限于监测数据有限，模型仅以药量和爆源距作为输入参数，导致部分数值预测误差偏大。

3 应用实例

大坪山新建隧道为泉厦高速公路的扩建隧道，原隧道为左右洞分离式隧道。新建左线位于原既有两隧道中间，全长1 088.3 m，距原洞净距分别为11.28、11.08 m；新建右线位于原既有隧道右洞外侧，全长1 082.5 m，距原洞净距5.28 m。新建隧道与原隧道构成四洞小净距隧道群（见图1）。主要穿越岩层燕山早期侵入花岗岩及其风化层，构造条件相对稳定，山顶地形波状起伏。隧道局部与3座城市隧道斜交，垂直最小净距仅5.1 m，形成7座小净距隧道群，且隧道山顶正上方及附近（最小仅44 m）有大量民房分布，施工力学形态极为复杂。为确保既有高速公路安全通行，对该工程爆破振动进行了全程监测。测点主要布置在先行洞中间岩柱迎爆侧边墙及拱肩处。表2～3列出了与本文有关的监测结果，其中Q1为单段最大药量。

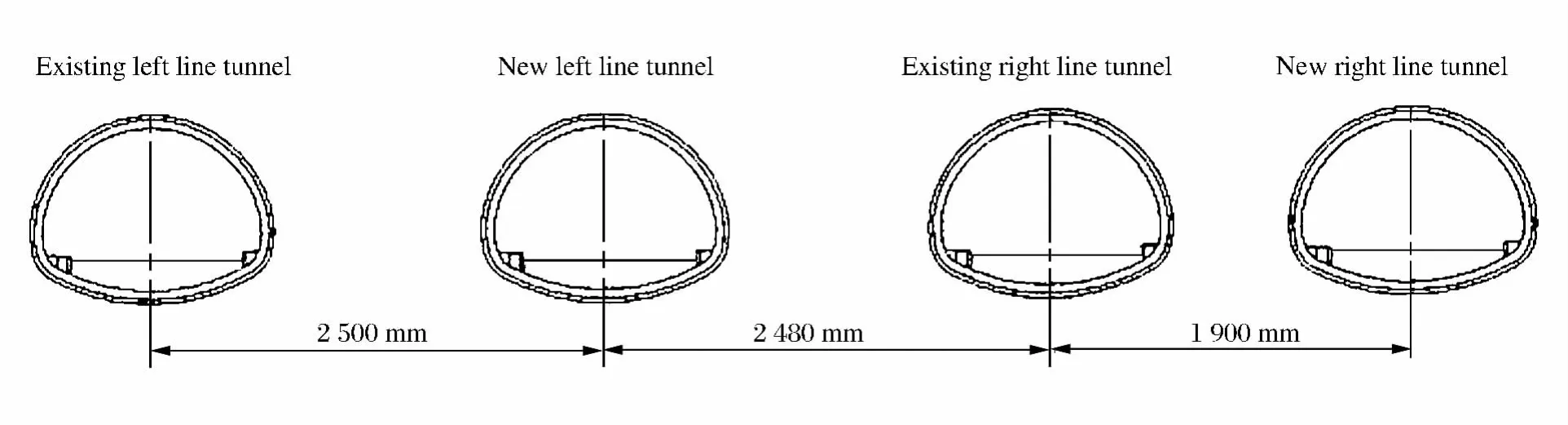
图1 大坪山各隧道关系图Fig.1 Relationships of Dapingshan tunnels

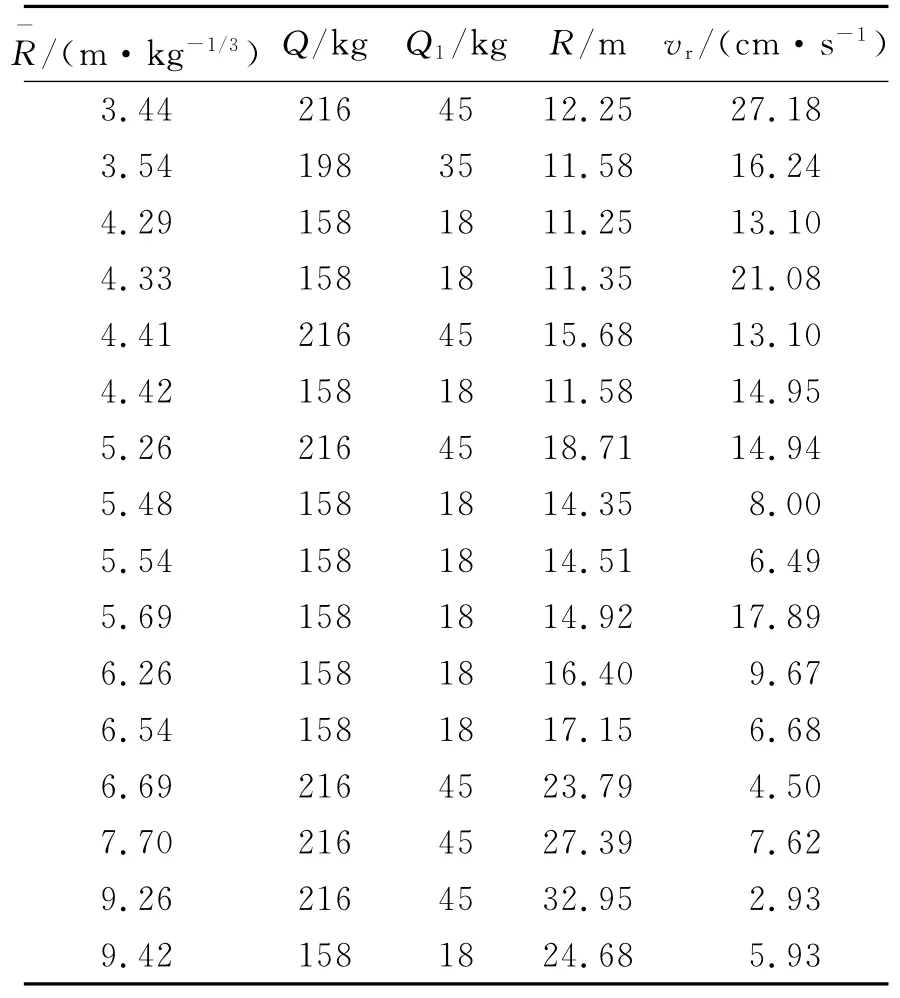
表2 新建左线隧道爆破、原右线隧道左侧壁质点峰值振速Table 2 The vibration peck velocity of the existing right line tunnel’s left wall by the new left line tunnel blasting

利用式（2）对表2～3中的质点振动速度监测数据进行回归，并作不同隧道爆破振速与比例距离的关系曲线，如图2～3所示。

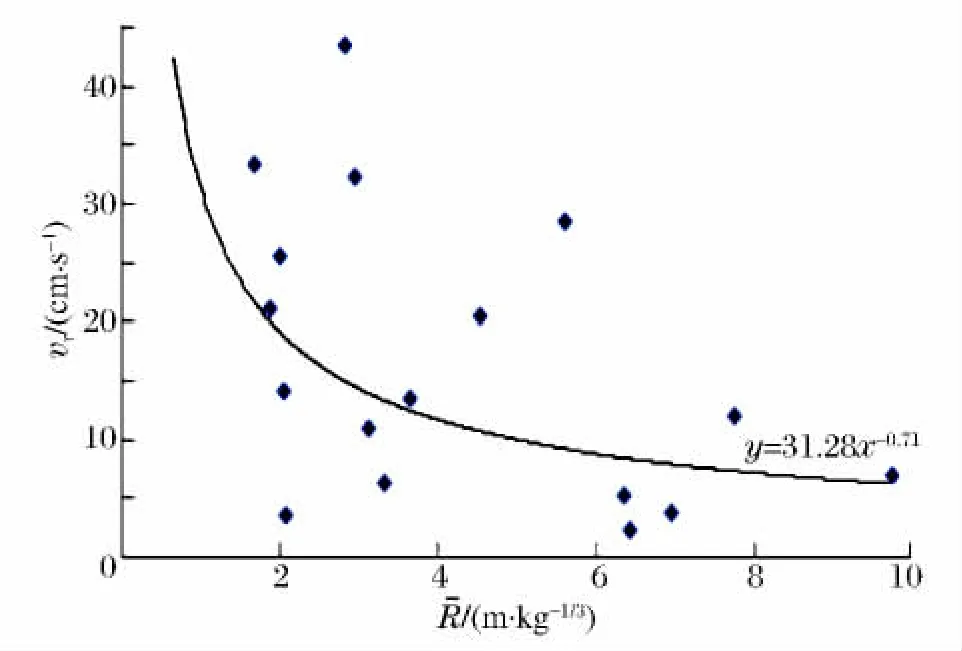
图3 新建右线爆破、既有右线右侧壁振速与比例距离的关系Fig.3 Relationships between vibration velocity and scaled distance of the existing right tunnel’s right side wall by the new right line tunnel blasting

依据第1节爆破分区划分的标准，对大坪山小净距隧道爆破分区进行细化。

由图2，新建左线隧道爆破分区为：比例距离在0～4.59范围内为近区；比例距离在4.59～8.38范围内为中区；比例距离大于8.38为远区。

由图3，新建右线隧道爆破分区为：比例距离在0～2.39范围内为近区；比例距离在2.39～6.13范围内为中区；比例距离大于6.13为远区。

以表3中17组数据为学习样本进行训练，预测表2中爆破近区参数（6组）下的振速。同时，利用拟合得到的萨道夫斯基经验公式（见图3）做相同的预测，预测结果如表4所示。

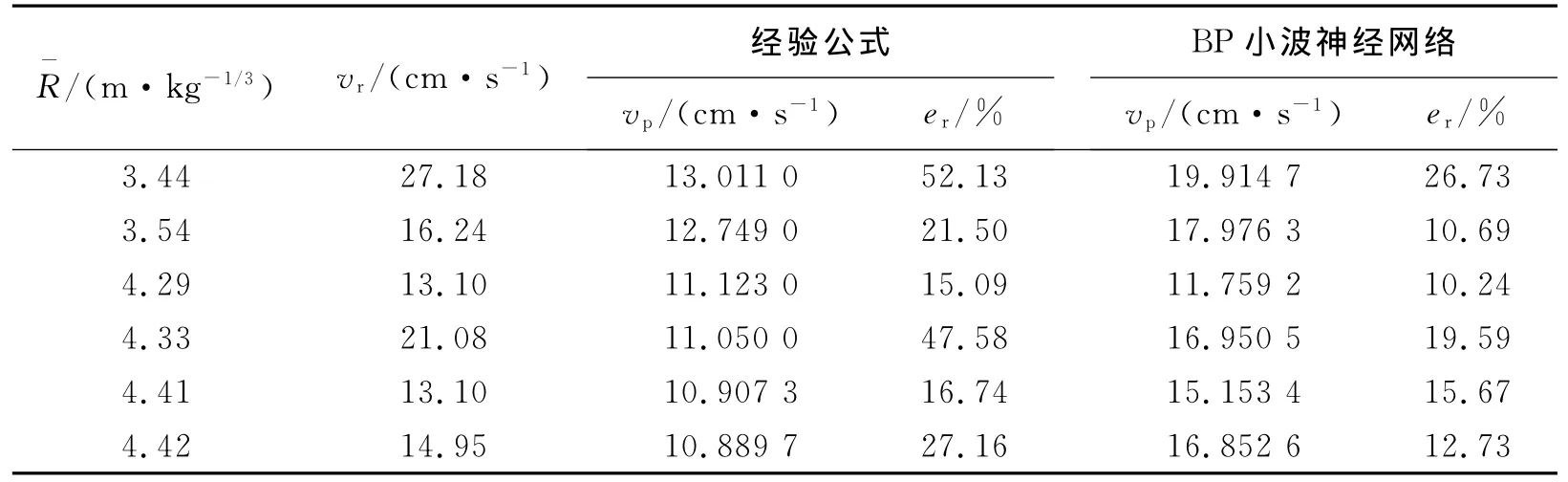
表4 大坪山隧道爆破近区实测振速与预测振速对比Table 4 Comparison of blasting vibration velocities near tunnel blasting source between site monitor and prediction in Dapingshan tunnel

由表4可知，经验公式预测误差的波动范围为15.09%～52.13%，平均相对误差为30.03%；BP小波神经网络预测误差的波动范围为10.24%～26.73%，平均相对误差为15.94%。

由图2～3及表4分析可知，BP小波神经网络预测相对误差与经验公式有较高的一致性，即经验公式预测误差大的数据，BP小波预测误差也较大。表4中第1组数据误差较大的原因是：第1组比例距离对应的实测振速偏离拟合曲线。因此，在使用BP小波神经网络模型时，应结合经验公式，剔除离散较大的数据。综上所述，萨道夫斯基经验公式无法合理预测临近既有隧道爆破近区振速，而BP小波神经网络可采用隧道右洞爆破数据对左洞爆破时的爆破近区振速进行较好的预测。

4 结 论

通过隧道爆破振动分区及隧道爆破近区的预测方法研究，可得出以下结论：

（1）根据装药量和爆源距确定测点离震源的比例距离绘制爆破振动速度衰减曲线，在无实测数据时，可将隧道爆破近、中、远区大致划分为：比例距离在0～5.0范围内为近区；比例距离在5.0～9.0范围内为中区；比例距离大于9.0为远区，再针对具体情况对隧道爆破分区进行修正。若有实测值，则应绘出速度衰减曲线后，以速度衰减曲线的斜率k′的大小划分隧道爆破近、中、远区。

（2）采用萨道夫斯基经验公式的方法分析爆破远、近区，爆破振动远区数据得出的规律不适用于爆破近区，而对本文中提出的BP小波神经网络预测方法则可不受此限制。BP小波神经网络爆破近区预测模型不仅适用于新建分离式隧道，也适用于临近既有隧道的新建小净距隧道。因此，在复杂环境下的隧道钻爆施工时，可依据BP小波神经网络对已测爆破数据进行分析，优化爆破施工方案，依据预测结果控制爆破振动大小，以保证隧道围岩的稳定性。但要发挥BP小波神经网络预测模型的优势，则需要大量前期近似环境条件下的监测数据，以反映爆破振动参数特征。

影响爆破振动的因素复杂多变，但限于监测数据有限，本文中仅以药量和爆源距作为输入参数，而未考虑岩土体性质变化等因素，一定程度影响了模型的预测性能，因此本文中建立的模型适用于爆破开挖区域的岩性、岩体结构和地质条件变化较小的预测。在今后的工程实践中，应依据实际情况量化地质地形条件，全面考虑影响爆破振动的主要因素，建立预测模型，进一步提高预测精度。

［1］谭忠盛，杨小林，王梦恕.复线隧道施工爆破对既有隧道的影响分析［J］.岩石力学与工程学报，2003，22（2）：281－285.Tan Zhong－sheng，Yang Xiao－lin，Wang Meng－shu.Effect of blast in double line tunnel on existing tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（2）：281－285.

［2］陈庆，王宏图，胡国忠，等.隧道开挖施工的爆破振动监测与控制技术［J］.岩土力学，2005，26（6）：964－967.Chen Qing，Wang Hong－tu，Hu Guo－zhong，et al.Monitoring and controlling technology for blasting vibration induced by tunnel excavation［J］.Rock and Soil Mechanics，2005，26（6）：964－967.

［3］刘玉山，陈建平.大轩岭小净距隧道爆破振动监测与分析［J］.爆破，2008，25（2）：92－94.Liu Yu－shan，Chen Jian－ping.Monitoring and analysis of blasting vibration in Daxuanling tunnel with small clear space［J］.Blasting，2008，25（2）：92－94.

［4］傅洪贤，赵勇，谢晋水，等.隧道爆破近区爆破振动测试研究［J］.岩石力学与工程学报，2011，30（2）：335－340.Fu Hong－xian，Zhao Yong，Xie Jin－shui，et al.Study of blasting vibration test of area near tunnel blasting source［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30（2）：335－340.

［5］Yang G L，Rocque P，Bawden W F，et al.Measurement and analysis of near－field blast vibration and damage［J］.Geotechnical and Geological Engineering，1994，12（2）：169－182.

［6］钟光复.岩石、混凝土介质中爆破近区破坏规律的研究［D］.合肥：中国科学技术大学，2006.

［7］逄焕东，陈士海.弹性介质中爆破地震波传播的分区变化规律研究［J］.振动与冲击，2009，28（3）：105－107.Pang Huan－dong，Chen Shi－hai.Study on the variation law of blasting seismic wave’s propagation in elastic media［J］.Journal of Vibration and Shock，2009，28（3）：105－107.

［8］陈士海，魏海霞，杜荣强.爆破震动信号的多分辨小波分析［J］.岩土力学，2009，30（增刊）：135－139，143.Chen Shi－hai，Wei Hai－xia，Du Rong－qiang.Multi－resolution wavelet analysis of blasting vibration signals［J］.Rock and Soil Mechanics，2009，30（suppl）：135－139，143.

［9］GB6722－2003，爆破安全规程［S］.

［10］饶增.隧道钻爆施工对初期支护的影响及控制标准的研究［D］.北京：北京交通大学，2010.