Grain型级联反馈移存器的非奇异性判定

王秋艳，金晨辉



Grain型级联反馈移存器的非奇异性判定

王秋艳，金晨辉

(解放军信息工程大学三院，郑州 450004)

Grain算法是欧洲序列密码工程eSTREAM最终入选的面向硬件实现的3个序列密码算法之一，它由2个反馈移存器和前馈函数组成，能有效抵御基于线性反馈移存器的序列密码攻击。针对以Grain算法为特例的Grain型级联反馈移存器的非奇异性判定问题，给出Grain型级联反馈移存器在初始化过程和密钥流生成过程中，状态刷新变换均构成双射的充分条件，并通过反例说明对于有限域上的Grain型级联反馈移存器，即使所使用的2个移存器都是非奇异的，并且前馈函数满足相应性质，其状态刷新变换仍可能不构成双射。利用Grain v1算法验证了该非奇异性判定结果的正确性。

序列密码；Grain算法；非线性反馈移存器；非奇异性；状态刷新变换；双射性

1 概述

线性反馈移存器的输出序列具有良好的密码学性质，目前很多序列密码算法都由线性反馈移存器和非线性前馈函数(或非线性有记忆变换)构成。然而，由于线性反馈移存器的输出信号之间存在线性制约性，从而产生很多针对基于线性反馈移存器设计的序列密码的攻击方法，如代数攻击[1]、快速相关攻击[2]等，促使人们寻找新的序列密码结构。在eSTREAM工程中，最终胜出的3个面向硬件实现的序列密码算法Grain算法[3]、Trivium算法[4]和Mickey算法[5]都是基于非线性反馈移存器设计。目前，基于非线性反馈移存器的设计已逐渐发展为序列密码设计的重要方式。

Grain算法[6-7]是一个典型的基于非线性反馈移存器设计的序列密码算法，为保证Grain序列密码算法的输出序列具有良好的密码学性质，Grain算法通过利用一个周期达到最大的线性反馈移存器控制一个非线性反馈移存器的方法设计其乱源结构。这种将线性反馈移存器和非线性反馈移存器有机结合的方式，为序列密码的设计提供了一个典型的模型。文献[8]对该模型的安全性进行了分析，对这种模型给出了一种区分攻击。文献[9]对该模型进行了代数攻击和相关攻击。文献[10]研究了其输出序列的周期性质。

反馈移存器的非奇异性[11]，也就是反馈移存器的状态刷新变换构成双射，是序列密码设计中对反馈移存器的基本要求。如果反馈移存器是奇异的，则其状态图将出现分叉现象，从而存在2个能产生相同的后续状态的移存器状态，此时基于该移存器设计的序列密码可能存在等效密钥，甚至可能遭遇基于相关(密钥-IV)对的差分攻击[12]。因此，在设计序列密码时，应该确保反馈移存器的非奇异性，以避免可能存在的安全隐患。

本文研究以Grain算法为特例的一类反馈移存器模型(称为Grain型级联反馈移存器)的非奇异性判定问题。给出能使其在初始化过程和密钥流生成过程中的状态刷新变换都构成双射的充分条件，并通过反例证明在一定条件下Grain型级联反馈移存器的状态刷新函数不能构成双射。

2 Grain型级联反馈移存器简介

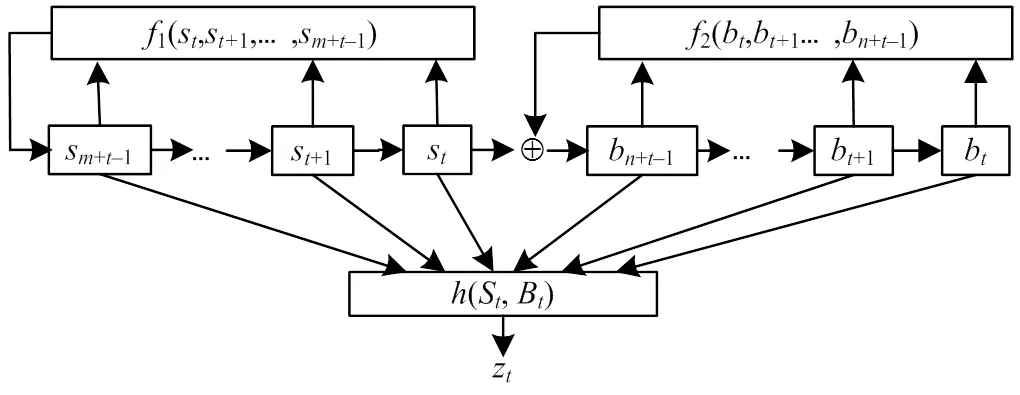
图1 Grain型级联反馈移存器的结构框图

在初始化过程和密钥流生成过程2种情形下，Grain型级联反馈移存器采取2种不同的状态刷新方式：

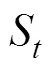
3 Grain型级联反馈移存器的非奇异性研究

首先给出Grain型级联反馈移存器在密钥流生成过程中状态刷新变换构成双射的充分条件。

定理1 设在Grain型级联反馈移存器中FSR1是非奇异的，则以下结论等价：

(2)Grain型级联反馈移存器中FSR2是非奇异的；

证明：由引理可知，结论(2)和结论(3)等价。下文证明结论(1)与结论(3)等价。

设结论(3)成立。由于Grain型级联反馈移存器的状态刷新变换为：

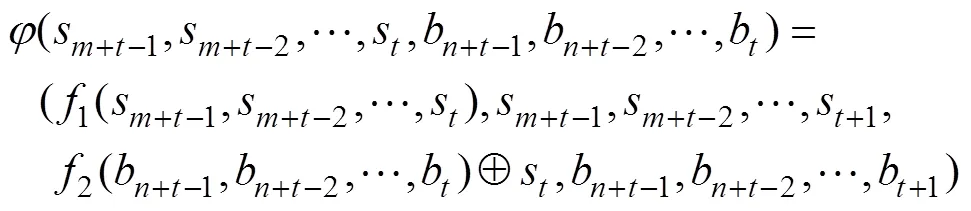
当以下等式成立时：

由Grain型级联反馈移存器的状态刷新变换定义可知：

且有：

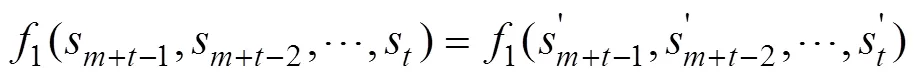
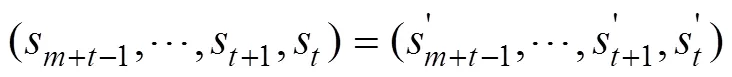
由此即知结论(1)与结论(3)等价。

然后给出Grain型级联反馈移存器在初始化过程中状态刷新变换构成双射的充分条件。

定理2 设在Grain型级联反馈移存器中FSR1和FSR2都是非奇异的，如果函数：

证明：Grain型级联反馈移存器在初始化过程的状态刷新变换为：

其中：

假设：

由Grain型级联反馈移存器的状态刷新变换定义可知：

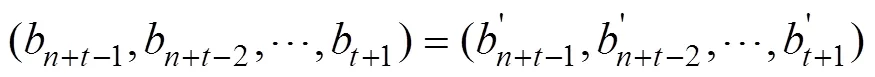
且有：

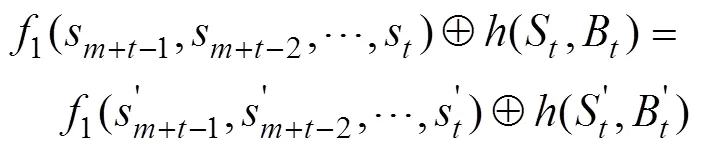
由定理1和定理2可知，为保证Grain型级联反馈移存器的状态刷新函数构成双射，只需将Grain型级联反馈移存器中的2个FSR都设计成非奇异反馈移存器，且前馈函数的输入变量都不抽自2个FSR的最低级即可。

定理3表明，即使前馈函数的输入变量从FSR2的最低级抽取，在一定条件下仍可保证Grain型级联反馈移存器的状态刷新函数构成双射。

定理3 设在Grain型级联反馈移存器中FSR1和FSR2是非奇异的，如果函数：

证明：Grain型级联反馈移存器在初始化过程的状态刷新变换为：

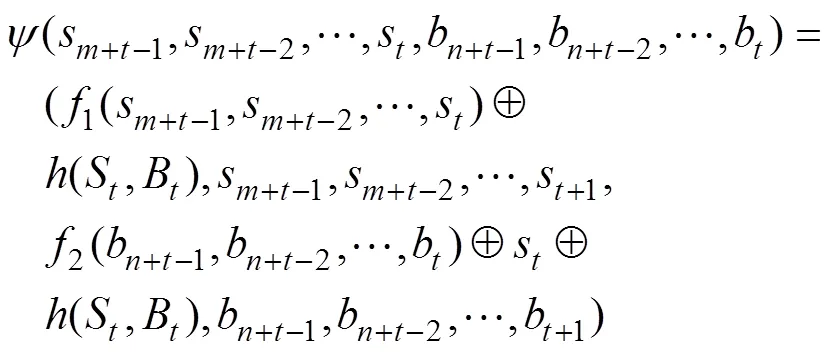
其中：

假设：

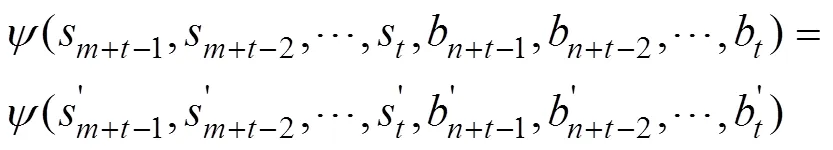
由Grain型级联反馈移存器的状态刷新变换定义可知：

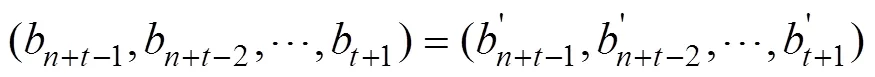
且有：

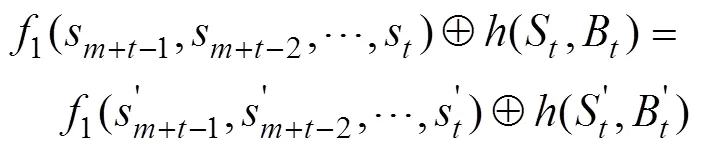
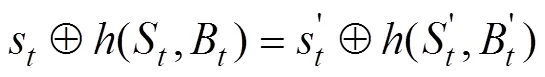
下面给出定理3的一个反例，当前馈函数满足定理3的条件，输入变量不从FSR2的最低级抽取，如果FSR1的反馈函数不满足定理3的条件，则Grain型级联反馈移存器的状态刷新函数就有可能构不成双射。

定理4 设Grain型级联反馈移存器中FSR1和FSR2的反馈函数满足：

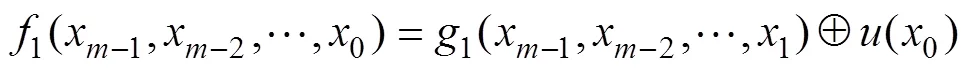
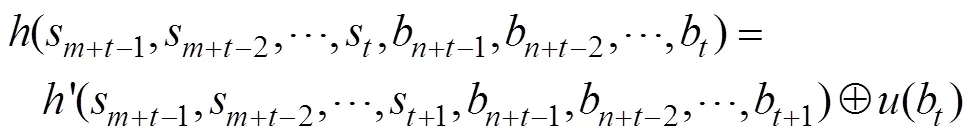
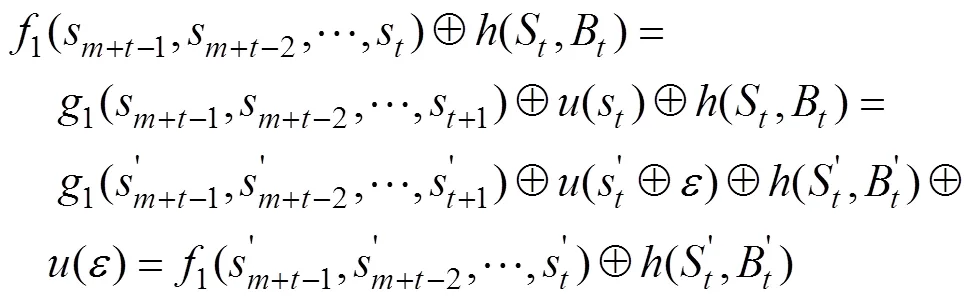
说明：

最后证明Grain v1算法在初始化过程和密钥流生成过程的状态刷新函数都是双射的。

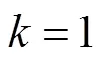
定理5 Grain v1算法在初始化过程和密钥流生成过程的状态刷新变换都是双射的。

4 结束语

本文研究了Grain型级联反馈移存器的非奇异性问题，给出了其在初始化过程和密钥流生成过程中状态刷新变换构成双射的2个充分条件，并举例说明了在一定条件下其状态刷新变换可能不构成双射，这些结果对于基于Grain型级联反馈移存器的序列密码的设计和分析具有实际的应用价值。通过本文分析可知，Grain型级联反馈移存器存在潜在弱点，必须谨慎选择其反馈函数和滤波函数以保证其安全性。在下一步的工作中，将进一步对Grain型级联反馈移存器的密码学性质进行分析，并研究该类移存器的构造问题。

[1] Courtois N T, Meier W. Algebraic Attacks on Stream Ciphers with Linear Feedback[C]//Proc. of EUROCRYPT’03. Warsaw, Poland: Springer-Verlag, 2003: 345-359.

[2] Meier W, Staffelbach O. Fast Correlation Attacks on Stream Ciphers[J]. Journal of Cryptology, 1989, l(3): 159-176.

[3] Hell M, Johansson T, Meier W. Grain——A Stream Cipher for Constrained Environments[EB/OL]. (2005-06-22). http://www. ecrypt.eu.org/stream/ciphers/grain/grain.pdf.

[4] de Cannière C. Trivium: A Stream Cipher Construction Inspired by Block Cipher Design Principles[C]//Proc. of ISC’06. [S. l.]: Springer-Verlag, 2006: 171-186.

[5] Babbage S. The Stream Cipher MICKEY-128 2.0[EB/OL]. (2006-08-18). http://www.ecrypt.eu.org/stream/p2ciphers/mickey128/ mickey128_p2.pdf.

[6] Maximov A. Cryptanalysis of the “Grain” Family of Stream Cipher[C]//Proc. of ASIACCS’06. New York, USA: ACM Press, 2006: 283-288.

[7] 宋海欣, 范修斌, 武传坤, 等. 流密码算法Grain的立方攻击[J]. 软件学报, 2012, 23(1): 171-176.

[8] 黄小莉, 武传坤. 对一种新的序列密码结构的密码分析[J]. 软件学报, 2008, 19(5): 1256-1264.

[9] Berbain C, Gilbert H. Algebraic and Correlation Attacks Against Linearly Filtered Non Linear Feedback Shift Registers[C]//Proc. of SAC’09. [S. l.]: Springer-Verlag, 2009: 184-198.

[10] Hu Honggang. Periods on Two Kinds of Nonlinear Feedback Shift Registers with Time Varying Feedback Functions[J]. International Journal of Foundations of Computer Science, 2011, 22(6): 1317-1329.

[11] Lai Xuejia. Condition for the Nonsingularity of a Feedback Shift Register over a General Finite Field[J]. IEEE Transac- tions on Information Theory, 1987, 33(5): 747-749.

[12] Wu Hongjun, Huang Tao, Nguyen P H. Differential Attacks Against Stream Cipher ZUC[C]//Proc. of ASIACRYPT’12. Beijing, China: [s. n.], 2012: 262-277.

编辑 陆燕菲

Criteria forNonsingularityof Grain-like Cascade Feedback Shift Register

WANG Qiu-yan, JIN Chen-hui

(The Third Institute, PLA Information Engineering University, Zhengzhou 450004, China)

Grain cipher is one of the 3 final hardware-oriented stream ciphers of the eSTREAM project, it is based on two feedback shift registers and a filtering function, and it can effectively resist stream cipher attacks based on linear feedback shift register. In this paper, the nonsingularity of the Grain-like cascade feedback shift registers is investigated, the sufficient conditions of state refresh transformations in initialization phase and key stream generation phase being bijective is given. As a counterexample, for the word-oriented Grain-like cascade feedback shift registers, even if the two feedback shift registers are both nonsingular, and the filtering function satisfies proper conditions, the state update transformation can also be nonbijective. It proves the result of criteria for nonsingularity by using Grain v1 algorithm.

stream cipher; Grain algorithm; nonlinear feedback shift register; nonsingularity; state refresh transformation; bijectivity

1000-428(2014)03-0167-04

A

TN918.1

国家自然科学基金资助项目(61272488, 61272041)。

王秋艳(1985－)，女，博士研究生，主研方向：密码学；金晨辉，教授、博士生导师。

2013-03-01

2013-04-02 E-mail：wangqiuyan06@gmail.com

10.3969/j.issn.1000-3428.2014.03.034