脑图像数据中的独立分量分析方法

马 斌，陈俊杰



脑图像数据中的独立分量分析方法

马 斌1，陈俊杰2

(1. 山西中医学院医药管理学院，太原 030024；2. 太原理工大学计算机与软件学院，太原 030024)

针对脑功能磁共振成像在处理数据时空间维数较大的问题，提出一种空间独立分量分析(ICA)方法。研究空间ICA方法的基本模型结构和空间ICA的3种常见算法，即Infomax算法、Fixed-Point算法和Orth-Infomax算法。设计中文词义辨别实验，并使用线性相关方法进行算法比较。实验结果表明，与Infomax算法、Fixed-Point算法相比，Orth-Infomax算法任务相关分量的时间序列与参考函数的平均相关系数最大，具有较高的求解质量和求解效率，能够有效处理脑功能磁共振成像系统中存在的大量数据。

脑功能磁共振成像；独立分量分析；一致任务相关成分；正交信息极大化算法；源信号；线性相关

1 概述

脑功能磁共振成像(functional Magnetic Resonance Im- aging, fMRI)是一种新型的高效无辐射非介入性损伤成像技术，已经成为广泛使用的脑功能研究手段[1]。基于血氧水平依赖的认知功能成像技术(BOLD)是fMRI方法应用的基础。当人的大脑开始执行相应任务时，大脑组织中的敏感区域会持续接收相应刺激，血红蛋白和脱氧血红蛋白两者之间的血氧水平比例会发生变化并造成该区域磁共振信号的改变，fMRI可以间接测量这种信号的改变，并通过产生的大量数据来研究人脑的基本活动规律。

针对人脑结构信息处理的特殊性和复杂性，从认知过程基于的生理假设机制上分析，fMRI数据处理方法主要分为2类，即基于神经功能模型的假设驱动方法和基于信号源本身结构的数据驱动方法[2]。本文提出的独立分量分析(Independent Component Analysis, ICA)方法是一种探测性的并基于数据分析的信息处理方法[3]。ICA方法在实际操作过程中不需要预先假设相关模型，而是直接抽取对应数据中所包含的特定信息，按照统计独立的原则，在原始信号采集基础上将收集到的多进程数据通过优化算法分解为若干相互独立的要素。

2 ICA数学模型分析

独立分量分析(ICA)是从多维统计数据中寻找潜在因子或成分的一种方法[4]。ICA应用于fMRI数据集合时，模型的建立是通过优化算法将所观察到的多进程实验信号分解为若干线性空间相互独立的成分。

假设()=[1(),2(),…,U()]T是个实验测量信号，它是由个独立的源信号()=[1(),2(),…,S()]T线性组合表示而成，对每一个时间点都有：

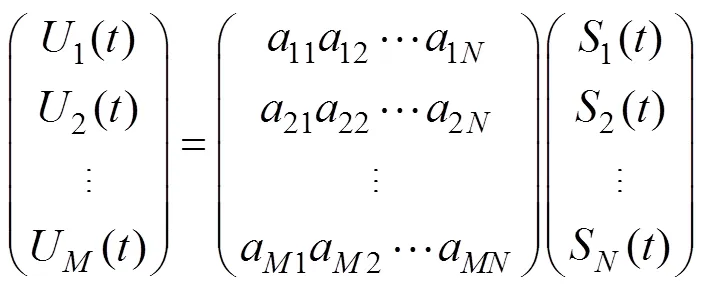
其向量矩阵的数学表达式为[5-6]：

()=()

其中，被估计的源信号()的各成分是统计独立的[7]；假设=且是×维混合矩阵；源信号是非高斯信号分布或最多只有一个是高斯信号分布[8]。

ICA算法目的是要根据实验测量数据得到分离矩阵，使得输出信号为()=()。其中，输出信号()是源信号()的一个估计且相互独立。其原理结构如图1所示。

图1 ICA算法原理结构

3 ICA的基本应用

文献[9]将ICA方法应用到fMRI数据处理过程。使用ICA中的Infomax算法分离观测到的fMRI信号，并成功获得持续任务相关分量(CTR)和瞬时任务相关分量(TTR)等数据参数。ICA方法尝试将多维数据变量分解成一个或若干个与实验任务相关的统计独立的分量。其基本思路是从分离出的独立分量中找到对应时间序列与实验的激励函数相关性最大的持续任务相关分量。对fMRI数据的处理可以使用空间独立分量分析(SICA)方法或时间独立分量分析(TICA)方法[10]，鉴于fMRI本身数据像素点的数量远大于其采样点的数量，在实际操作过程中，通常使用SICA方法研究和分析fMRI数据[11]。

4 ICA的空间独立分量分析

SICA所基于的假设是与认知过程脑激励区间相独立进行的，其方法是扫描每个时间点对应的图像数据，分析处理后得到相对独立的时间序列，表示激活区脑的神经元强度随时间的变化过程。

4.1 空间独立分量算法分析

近年来，用于处理fMRI数据的SICA算法主要有信息极大化算法(Infomax算法)[12]、快速不动点算法(Fixed-Point算法)[13]和正交信息极大化算法(Orth-Infomax算法)。Infomax算法主要用来得到fMRI数据的原始特征以便深入研究；同时它利用数据中有效的移出来研究各激活区域之间的功能联系[14]；文献[15]通过Infomax算法得到fMRI数据在独立刺激条件下血流动力学的变化趋势。Fixed-Point算法用来衡量脑信号的统计独立性并对非结构化的信号数据进行分离以便深入研究[16]；文献[17]比较了Infomax算法和Fixed-Point算法的差异，对模型的总体估计和滤波能力上有优势的是Infomax算法，而Fixed-Point算法的空间准确性和时间准确性要略优于Infomax算法。在研究fMRI数据处理问题时，提出了一种改进的梯度学习算法，即正交信息极大化算法(Orth-Infomax)。这个算法综合了Infomax算法和Fixed-Point算法的优点，具有较快的收敛速度和更准确的分离精度。对于大量的实际fMRI数据来说，Orth- Infomax算法具有最佳的估计脑内激活时间动力学准确性。

4.2 实验设计

对上述3个算法分别测试，进行fMRI数据的空间独立分量研究，并采用线性相关方法分析实验结果。

实验对象是5名健康的大学生，视力正常，右利手，无色盲，无精神病史。实验任务为中文词义辨别，要求被试对象判断所呈现的中文词语对是否为反义词，内容包含中文词对96组，其中一半为反义词词对(如大-小，多-少、前-后)，另一半则是随意搭配词对(如计算机-国家、中医-建筑学)。如果是反义词对，测试者就按下蜂鸣器按钮，主试可以同步记录被试的反应情况。实验采用组块设计，组块刺激呈现分为12组，每组8对刺激(包含中文反义词对和随意搭配词对)，每对刺激交替出现，且出现时间设定为1 s。当第2个刺激表现完成后，间隔1 s的时间段，开始操作下一组刺激信息。

功能像扫描参数设置为：TR=4 000 ms; TE=50 ms; FOV (Field of View)=375×240 mm; Flip=60;像素矩阵=126×36; slice thickness=6 mm;无间隔。三维解剖像参数设置为：TR= 20 ms; TE=6 ms; FOV(Field of View)=240×240 mm; Flip=60;像素矩阵=240×240; slice thickness=2 mm;无间隔。

4.3 实验结果

设计一个与实验任务的BOLD脉冲反应函数相匹配的参考函数，成分图的时间序列用的列来表示，计算的值与参考函数间相关系数的大小即可表示实验操作任务与时间序列的相关性。实验过程中把最大的相关系数时间序列对应的成分图定义为一致任务相关成分(CTR)[18]。相关系数的平均值越大，说明算法估计激活时间动力学准确性越高。本文实验求得3个算法的CTR成分与参考函数的相关系数如表1所示。

表1 基于3种算法所得CTR成分与参考函数的相关系数

相关系数的平均值分别为：Orth-Infomax算法(0.797)；Fixed-Point算法(0.781)；Infomax算法(0.772)；依据图2所示分析，显然，Orth-Infomax算法得到的一致任务相关成分的时间序列与参考函数的平均相关系数最大。因此，Orth- Infomax算法的估计激活时间动力学准确性最高，能够高效地研究fMRI数据。

图2 3种算法的任务相关分量比较

将3种算法分析求得的CRT成分进行标准化操作，使用脑功能成像系统软件SPM以相同的阈值处理后，得到其激活状态表示如图3所示。

图3 3种算法得到的一致任务相关成分激活比较

5 结束语

本文研究了ICA的基本模型结构，论述了ICA应用于fMRI数据处理的基本情况，分析讨论了ICA空间独立分量的应用问题，着重介绍了Orth-Infomax算法、Fixed-Point算法和Infomax算法各自的特点，并基于实验所得的时间序列与参考函数的相关系数的大小，比较得出Orth-Infomax算法具有一定的优势。

不过，当前ICA方法在fMRI的具体应用中仍然存在许多问题，需要不断对其进行改进和完善。下一步的工作主要包括：

(1)本文实验是在单任务条件下得到的结果。在多任务的情况下，对复杂大脑高级活动的探测过程中，不能假定不同任务所激活的脑空间是独立的，因此，要结合具体的认知任务，进一步探讨利用ICA处理更有价值信息的问题。

(2)算法的改进和应用。现实世界需要构造更符合实际的模型，面对不同性质的数据时，要提出更有针对性的新算法来解决问题。ICA算法已经应用到语音信号处理、生物医学信号处理等领域。因此，算法的改进应用将是未来研究的重点。

[1] Norman K A, Polyn A M, Detre G J, et al. Beyond Mind- reading: Multi-voxel Pattern, Analysis of fMRI Data[J]. Trends in Cognitive Science, 2006, 10(9): 424-430.

[2] 张志强, 王世杰, 卢光明. 功能磁共振数据处理分析的原理及应用[J]. 中国医学影像技术, 2004, 20(10): 1632-1635.

[3] 唐焕文, 唐一源, 郭崇慧, 等. 神经信息学及其应用[M]. 北京: 科学出版社, 2007.

[4] Svensen M, Kruggel F, Benali H. ICA of fMRI Group Study Data[J]. Neuro Image, 2002, 16(3): 551-563.

[5] Cichocki A, Amari S I. Adaptive Blind Signal and Image Processing Learning Algorithms and Applications[M]. [S. l.]: Wiley, 2002.

[6] Girolami M. Self-organising Neural Networks-independent Component Analysis and Blind Source Separation[M]. [S. l.]: Springer-Verlag, 1999.

[7] Friston K J. Modalities, Modes, and Models in Functional Neuroimaging[J]. Science, 2009, 326(5951): 399-403.

[8] Hyvarinen A, Karhunen J, Oja E. Independent Component Analysis[M]. New York, USA: John Wiley, 2001.

[9] 李 可, 闫 镔, 单保慈. 功能磁共振图像处理的ICA方法综述[J]. 中国图象图形学报, 2005, 10(5): 561-566.

[10] 唐焕文, 张伟伟, 史振威, 等. 新的ICA算法实现成组fMRI信号盲分离[J]. 大连理工大学学报, 2007, 47(5): 773-776.

[11] 龙志颖, 姚 力, 赵小杰, 等. 空间ICA在fMRI数据上的应用与分析[J]. 中国医学物理学杂志, 2003, 20(4): 219-221.

[12] Bell A, Sejnowski T. An Information-maximization Approach to Blind Separation and Blind Deconvolution[J]. Neural Computation, 1995, 7(6): 1129-1159.

[13] Hyvarinen A. Fast and Robust Fixed-point Algorithm for Independent Component Analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634.

[14] Arfanakis K, Cordes D, Haughton V M, et al. Combining Independent Component Analysis and Correlation Analysis to Probe Interregional Connectivity in fMRI Task Activation Datasets[J]. Magn Reson Imaging, 2000, 18(8): 921-930.

[15] Duann J R, Jung T P, Kuo W J, et al. Single-trial Variability in Event-related BOLD Signals[J]. Neuro Image, 2002, 15(4): 823-835.

[16] Kiviniemi V, Kantola J H, Jauhialnen J, et al. Independent Component Analysis of Nondeterministic FMRI Signal Sources[J]. Neuro Image, 2003, 19(2): 253-260.

[17] van Eijsden P, Hyder F, Rothman D L, et al. Neurophysiology of Functional Imaging[J]. Neuro Image, 2009, 45(4): 1047- 1054.

[18] Bassett D S, Bullmore E. Small-world Brain Network[J]. Neuro Scientist, 2006, 12(6): 512-523.

编辑 顾逸斐

Independent Component Analysis Method in Brain Image Data

MA Bin1, CHEN Jun-jie2

(1. School of Medical Management, Shanxi College of Traditional Chinese Medicine, Taiyuan 030024, China; 2. College of Computer and Software, Taiyuan University of Technology, Taiyuan 030024, China)

Independent Component Analysis(ICA) is an effective method of data processing of the brain functional Magnetic Resonance Imaging(fMRI). Aiming at the feature that the spatial dimension of fMRI data is large, spatial ICA is selected to be discussed. The basic model structure of ICA and the three common algorithms of spatial ICA are deeply researched, including Infomax algorithm, Fixed-Point algorithm and Orth-Infomax algorithm. Chinese word meaning differentiation experiment is designed and analyzed with the linear correlation method. Experimental results show that, the time series of CTR in the Orth-Infomax algorithm has the maximum average correlation coefficient with the reference function, compared with Infomax algorithm and Fixed-Point algorithm, which has the high quality of the solution and the solving efficiency and can efficiently process the fMRI system data.

brain functional Magnetic Resonance Imaging(fMRI); Independent Component Analysis(ICA); consistently task-related component; Orth-Infomax algorithm; source signal; linear correlation

1000-3428(2014)03-0205-03

A

TP393.41

国家自然科学基金资助项目“基于fMRI的个性化图像情感标注及其本体库研究”(60970059)。

马 斌(1979－)，男，讲师、硕士、CCF会员，主研方向：人工智能，数据挖掘；陈俊杰，教授、博士生导师。

2012-12-27

2013-03-31 E-mail：mbsxtcm@163.com

10.3969/j.issn.1000-3428.2014.03.043