一种基于模糊Petri网的双向并行推理算法

王慧英，乐晓波，周恺卿



一种基于模糊Petri网的双向并行推理算法

王慧英1，乐晓波1，周恺卿2

(1. 长沙理工大学计算机与通信工程学院，长沙 410114；2. 马来西亚理工大学计算学院，马来西亚 士古来 80310)

基于模糊Petri网的并行推理算法的矩阵维数越大，其算法的时间复杂度也就越高。针对反向搜索压缩模糊Petri网模型的相关理论和并行推理算法的特点，结合矩阵命令提出一种实现双向推理的矩阵运算机制，以及其对应的基于模糊Petri网的双向并行推理算法。在使用一般模糊推理算法的过程中，推理矩阵为(11´8)维的模糊Petri网模型，而使用改进算法进行双向推理时所涉及的推理矩阵阶数仅为(7´6)。实验结果表明，与一般的模糊推理算法和反向搜索算法相比，该算法能够提高整个推理过程的并行度，降低算法的时间复杂度，从而提高推理效率。

模糊Petri网；矩阵运算；并行推理；反向搜索；双向推理

1 概述

Petri网是一种可以用网状图形表示的系统模型[1]，由Carl Adam Petri博士在其论文《用自动机通信》中首次提出相关的概念。由于Petri网中库所的输入、输出都只有“有”或者“无”这2种状态，利用传统Petri网模型难以有效描述现实世界中大量复杂的、不精确的、具有模糊行为的系统。学者们把Petri网模型与模糊数学联系在一起，提出了模糊Petri网(Fuzzy Petri Nets, FPN)模型[2]。FPN增强了Petri网表示和处理模糊知识的能力。将FPN应用于模糊知识的表达与模糊推理(Fuzzy Reasoning, FR)，是构造专家系统的一种良好建模工具[3]。文献[4]提出的基于Petri网可达图的FR算法，是在图形结构的基础上沿用分布加判断的方法进行搜索，此算法充分利用了Petri网的图形描述能力，而且思路比较清晰。近年来一些学者对基于FPN的推理算法做了一些研究[5-7]。文献[5]利用查询技术实现模糊推理，适合于大规模的FPN系统模型。文献[6]采用反向搜索(Reverse Search, RS)方法把与问题有关的一部分规则从知识库的系统中分离出来进行推理计算，满足了实时性的要求。文献[7]利用矩阵运算实现FPN推理算法的并行性。基于FPN并行推理算法的提出，充分利用了FPN的并行处理能力，具有推理效率高、便于操作处理的特点。本文在已有正反推理算法的基础上提出一种改进的基于FPN的双向并行推理(Bi-directionalParallel Reasoning, BDPR)算法，使用矩阵命令作为正反推理的切入点，以压缩矩阵的维数，并用实际推理算例验证了其正确性与可行性。

2 模糊Petri网及其相关定义

根据实际应用背景的不同，专家给出的FPN形式化定义不尽相同。本文采取一种基于模糊推理的FPN形式化定义，包括库所、变迁、确信度、阈值、权值5个部分[8]，具体形式由定义1给出。

定义1 FPN=(,,,,,,,0)

其中：

(1)={1,2,…,p}表示库所的有限集合，表示规则中库所的个数；

(2)={1,2,…,t}表示变迁的有限集合，表示规则中变迁的个数；

(3)()为输入(输出)函数，即库所与变迁之间的映射关系；

(7)0：→(0,1]表示初始标识，即推理开始时库所中的托肯数为命题的初始置信度。

在基于FPN的模糊推理系统中，库所表示推理的命题。变迁表示模糊推理的规则，即2个命题之间的因果关系。库所中的托肯数表示命题的真实度。变迁的置信度表示推理规则的可信度。

3 FPN模型的产生式规则

3.1 模糊变迁的使能规则

对于规则系统中的任意变迁，如果它所有输入库所上的标记值与相应输入弧上权值之积的和大于等于变迁的阈值，则变迁是使能的。

3.2 模糊产生式规则的基本形式

FPN可以用来描述模糊生成规则，利用FPN表达一些专家系统中不确定的逻辑推理关系。如果给出FR的初始条件，就可以利用推理算法计算出推理结果的可信度。定义3给出了一个FPN的模糊产生式规则的表示形式。

定义3=(1,2,…,R)，R(=1,2,…,)表示系统中的基本规则。其中，模糊产生式的2个基本规则所对应的FPN模型的表示形式如下所示：

图1 “与”规则的FPN表示形式

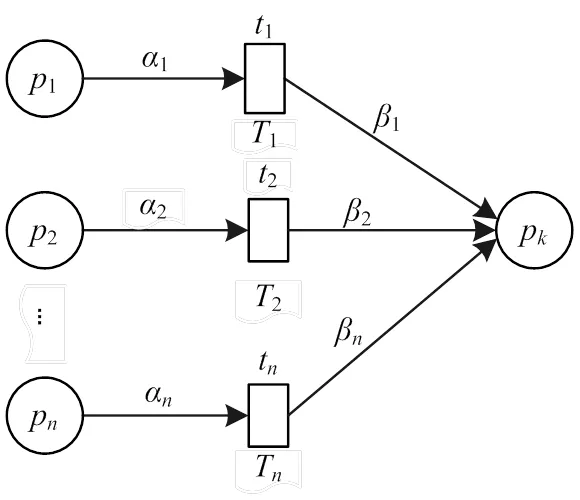
图2 “或”规则的FPN表示形式

4 BDPR算法

假设在某个推理过程中有个命题，个推理规则，则对应于FPN模型中，用个库所表示个命题，用个变迁表示个推理规则。

4.1 基本定义

4.1.1 矩阵命令符

在矩阵运算中，为删除某行或者某列，定义矩阵命令符如下：

定义4将所有要删除的行标顺序排列成向量，然后用命令“矩阵变量名”(,:)=[];%可删除与“矩阵变量名”对应矩阵中的指定行(通过指定)，并改变原矩阵的行维数。将所有要删除的列标顺序排列成向量，然后用命令“矩阵变量名”(:,)=[];%可删除与“矩阵变量名”对应矩阵中的指定列(通过指定)，并改变原矩阵的列维数。

4.1.2 极大代数算子

根据MYCIN[9]系统的思想定义以下极大代数算子。

4.1.3 关联矩阵和向量的定义

根据第2节模糊Petri网模型的定义以及双向并行推理算法的过程列出如下所需的关联矩阵和向量。

(1)定义关联矩阵={h}(=1,2,…,;=1,2,…,)：

(2)库所向量=(1,2,…,x)T，||=||；如果p是要求的结果库所或者相关的输入库所，则x=1，否则x=0。

(3)变迁向量=(1,2,…,y)T，||=||；如果t是与结果命题相关的变迁，则y=1，否则y=0。

(7)定义库所置信度向量=(1,2,…,m)T，mÎ[0,1] (=1,2,…,)。

4.2 算法设计

(1)求解初始库所向量和变迁向量以及关联矩阵。令=1，初始库所向量0=(1,2,…,x)T，若p是结果命题，则x=1；否则x=0。初始变迁向量0=(01,02,…,0)T。

(3)定义向量=(“向量中元素0所在的位置数”)，定义=(“向量中元素0所在的位置数”)。(,:)=[ ]；(:,)=[ ]，最终得到的是维数减少的输入输出矩阵、；(,:)=[ ]，得到新的阈值向量。(,:)=[ ]，得到新的置信度向量。

(4)此时推理对应的是个库所个变迁的模糊产生式规则的知识系统。初始化=0，向量max=0。计算变迁的输入强度值，1=T×，其中，=[1,2,…,i]T。

(6)计算输入强度1=，并将输入强度与变迁阈值进行比较，如果+1大于阈值，则变迁触发。

(8)计算1=1得到所有库所新的置信度。将该置信度向量与上一次循环所得置信度向量进行比较，若置信度向量有变化，则令1，返回步骤(4)继续计算；若置信度向量无变化，则推理结束。

4.3 算法分析

4.3.1 算法的可行性分析

项目管理系统：根据科研项目的特点，对项目申报、立项、实施、验收过程中所需财务信息的归集、整理、提取和分析进行科学全面的设计。采用传统的办法，难以及时有效地掌握最新的科研情况，而且每次查询统计工作量浩大，通过本系统对科研项目实现项目分级、分类管理，使各级领导不但可以对所承接的各类项目及取得的成果一目了然，也能对未来的发展具有一定的预测。

BDPR算法的流程如图3所示。

图3 双向并行推理算法流程

鉴于正向矩阵算法的并行性及反向搜索算法的实时性，采用矩阵命令“矩阵变量名”(,:)=[]和命令“矩阵变量名”(:,)=[]把正反推理结合在一起进行矩阵运算，提出一种基于矩阵运算的FPN的BDPR算法。利用反向矩阵推理求解与结果命题相关的前提命题和规则；根据矩阵命令删除不需要的库所和变迁，即把与问题无关的一部分规则先从知识库的系统中删除，得到维数减少的矩阵形式；通过矩阵正向推理得到需要的结果值。整个推理算法都是通过矩阵运算实施的，所以具有很好的并行性及高效性。

4.3.2 算法的复杂性分析

5 算法实例分析

设知识库系统有如下推理规则(表示输出强度)：

规则1 if1(0.6) and2(0.4)then4(=0.8)；

规则2 if2(1) then5(=0.9)；

规则3 if2(0.3) and3(0.7) then9(=0.8)；

规则4 if4(0.9) then6(=0.7)；

规则5 if5(0.5) then6(=0.8)；

规则6 if5(0.5) then8(=0.9)；

规则7 if6(0.8) then7(=0.9)；

规则8 if9(0.9) then10(=0.6) and11(=0.9)。

知识库系统对应的FPN模型如图4所示。

图4 知识库系统的FPN模型

已知系统的初始置信度向量0=(0.8,0.9,0.8,0.8,0.9,0,0, 0,0.9,0.8,0.9)T，阈值向量=(0.2,0.3,0.5,0.4,0.5,0.4,0.2,0.5)T，需要求解的是知识库系统中目标库所7、8的置信度。首先依据一般的FR算法和RS算法求解目标库所的置信度值，然后利用BDPR算法的推理过程求解目标库所的置信度值。由3种算法的推理结果对比验证本文算法的高效性。

(1)一般的FR算法

根据一般的FR算法的步骤可知输入矩阵和输出矩阵如下：

由FR推理可知：

1=(0.8,0.9,0.8,0.8,0.9,0.504,0,0.405,0.9,0.8,0.9)T

2=(0.8,0.9,0.8,0.8,0.9,0.504,0.363,0.405,0.9,0.8,0.9)T

3=(0.8,0.9,0.8,0.8,0.9,0.504,0.363,0.405,0.9,0.8,0.9)T

由于3=2，因此此时推理结束，得目标库所7、8

的最终置信度值分别为0.363、0.405。

(2)RS算法

对于FPN模型，首先采用逆向搜索策略对初始的FPN进行约简，根据所求的目标库所，针对每一个库所建立可达性集合、立即可达性集合以及相邻库所集合[13]。通过RS算法求得运算中所需的库所和变迁。不需要参加运算的库所和变迁值则设置为0。RS算法后输入矩阵和输出矩阵值如下：

由RS算法推理过程可知：

1=(0.8,0.9,0.8,0.9,0.504,0,0.405)T

2=(0.8,0.9,0.8,0.9,0.504,0.363,0.405)T

3=(0.8,0.9,0.8,0.9,0.504,0.363,0.405)T

由于3=2，因此此时推理结束，得目标库所7、8的最终置信度值分别为0.363、0.405。

(3)BDPR算法

根据BDPR算法的推理过程，由步骤(2)反向搜索运算可得=(1,1,0,1,1,1,1,1,0,0,0)T，=(1,1,0,1,1,1,1,0)T。然后根据步骤(3)可得矩阵、如下：

阈值向量=(0.2,0.3,0.4,0.5,0.4,0.2)T，置信度向量0= (0.8,0.9,0.8,0.9,0,0,0)T。由BDPR算法的推理过程可知：

1=(0.8,0.9,0.8,0.9,0.504,0,0.405)T

2=(0.8,0.9,0.8,0.9,0.504,0.363,0.405)T

3=(0.8,0.9,0.8,0.9,0.504,0.363,0.405)T

由于3=2，因此此时推理结束，得目标库所7、8的最终置信度分别为0.363、0.405。

3种推理算法的对比如表1所示。通过上述结果分析，将本文所提出的BDPR算法应用到实际推理过程中，可得到与FR算法、RS算法同样正确的推理结果。然而对于´阶矩阵来说，BDPR算法与FR和RS算法的时间复杂度都是(´)，矩阵维数越大，时间复杂度也越大。在FR算法中，推理过程所涉及的运算矩阵是(11´8)维的，而在BDPR算法中，推理过程所涉及的运算矩阵是(7´6)维的，由此可见，BDPR算法有较好的时间复杂度。由BDPR算法和RS算法的推理过程对比可知，BDPR算法具有较好的双向并行性的特点。从表1中3个推理过程的对比分析不难看出，BDPR算法不仅充分利用了FPN的并行推理能力，同时有效压缩了运算矩阵的维数，大大降低了算法的时间复杂度，从而有效提高了推理效率。

表1 BDPR算法和FR、RS算法的结果对比

6 结束语

本文在正向推理和反向搜索的基础上提出了一种基于FPN的BDPR算法。此算法充分利用FPN的并行处理能力，把正向推理与反向搜索结合在一起，不仅可以压缩推理运算中矩阵的维数，而且可以有效提高推理过程的并行度，进而降低推理过程的时间复杂度。通过实例验证了算法的正确性与可行性。将本文所提出的基于FPN的BDPR算法应用于实际的推理过程，可有效提高推理效率，具有一定的实际意义和应用价值。下一步将在Matlab平台上编程实现该双向并行推理算法。

[1] 袁崇义. Petri网原理与应用[M]. 北京: 电子工业出版社, 2005.

[2] 蒋昌俊. Petri网的行为理论及其应用[M]. 北京: 高等教育出版社, 2003.

[3] Zhang Baiyi, Cui Shangsen. A Parallel Backward Reasoning Study Using Fuzzy Petri Net[C]//Proc. of International Conference on Computer Science and Software Engineering. Wuhan, China: [s. n.], 2008: 315-319.

[4] Chen Shyiming, Chang Jinfu. Knowledge Representation Using Fuzzy Petri Nets[J]. IEEE Transactions on Knowldege and Data Engineering, 1990, 2(3): 311-319.

[5] 鲍培明. 基于查询方式的模糊Petri网的推理算法[J]. 计算机工程, 2004, 30(4): 70-72.

[6] 杨劲松, 凌培亮. 一种FPN的逆向知识推理方法设计实 现[J]. 计算机学报, 2009, 36(12): 158-160.

[7] 高梅梅, 吴智铭. 模糊推理Petri网及其在故障诊断中的应用[J]. 自动化学报, 2000, 26(5): 677-680.

[8] 傅卓君, 黄 璜, 李 洋. 一种新的模糊Petri网推理机制[J]. 计算机工程, 2011, 37(14): 202-204.

[9] 黄可鸣. 专家系统导论[M]. 南京: 东南大学出版社, 1988.

[10] 杨智应. 若干算法的复杂性分析问题研究[D]. 复旦大学, 2004.

[11] 杨晓波. 算法时间复杂性分析综述[J]. 西藏大学学报, 2011, 26(1): 87-90.

[12] 徐 欢, 李孝忠. 一种基于模Petri网的并行推理算法[J]. 系统仿真学报, 2007, 19(1): 108-113.

[13] 谭 旭, 陈英武. 一种新的Petri网推理算法在贫血诊断中的应用[J]. 计算机工程与应用, 2006, 42(11): 222-224.

编辑 任吉慧

A Bi-directional Parallel Reasoning Algorithm Based on Fuzzy Petri Nets

WANG Hui-ying1, YUE Xiao-bo1, ZHOU Kai-qing2

(1. School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha 410114, China; 2. Faculty of Computing, Universiti Teknologi Malaysia, Skudai 80310, Malaysia)

Time complexity of the parallel reasoning algorithm based on Fuzzy Petri Nets(FPN) is related to the dimension of matrix, and it will increase when the scale of the FPN becomes larger. By analyzing the characteristics of the parallel reasoning algorithm and the relevant theories of the Reverse Search(RS), this paper proposes a novel Bi-directional Parallel Reasoning(BDPR) algorithm based on FPN. As for the model of FPN with the dimension of 11 rows and 8 columns, if using the BDPR algorithm, the reasoning matrix order is 7 rows and 6 columns. Experimental analysis shows that the BDPR algorithm can effectively improve the parallelism of the whole process of reasoning, reduce the time complexity of algorithm, and improve the efficiency of reasoning, compared with a general Fuzzy Reasoning(FR) algorithm and an RS algorithm.

Fuzzy Petri Nets(FPN); matrix operation; parallel reasoning; Reverse Search(RS);bi-directional reasoning

1000-3428(2014)03-0208-05

A

TP301

国家自然科学基金资助项目(61170199)；湖南省自然科学基金资助项目(08JJ3124)。

王慧英(1989－)，女，硕士研究生，主研方向：Petri网行为理论及应用，人工智能；乐晓波，教授；周恺卿，博士研究生。

2012-12-24

2013-04-02 E-mail：523953309@qq.com

10.3969/j.issn.1000-3428.2014.03.044