一种递归π演算向Petri网的转换方法

康 辉，张双双，2，梅 芳

（1.吉林大学，计算机科学与技术学院，长春130012；2.吉林信息安全测评中心，长春130062）

随着面向服务的计算（Service-oriented computing SOC／Service-oriented architecture，SOA）技术［1］和业务流程管理（Business process management，BPM）技术［2］的广泛应用以及对软件可信性要求越来越高，很多学者用π演算和Petri网作为服务组合和业务流程技术的理论基础。π演算用来描述拓扑结构动态变化的并发系统，通过相应的数学分析方法，对系统的属性和行为进行分析。但是π演算［3－7］的进程表达式比较繁琐，不能形象地反应系统物理结构信息，不能刻画系统的真并发行为，而且从系统验证角度来看，其支持工具少，仅有MVB和HAL等几种自动验证工具，这样给后续的形式化验证带来了困难。Petri网［8－9］是一种形式化图形验证工具，它侧重于系统的结构描述和性质分析，并且能有效地刻画系统真正的并发语义。它是一种可用网状图形表示的系统模型［10－11］，适合描述异步、并发、分布式的系统，既可用于静态的结构分析，又可用于动态的行为分析。

由于π演算存在固有缺陷，很多学者已经在将π演算向Petri网转换这方面做了很多研究［12－13］，例如Raymond Devillers［12］等人已经提出了其转换的一般方法。但是对于π演算中递归结构的转换，目前仍然空白。在π演算中，对递归的表达是其基本的语义，较为简单；而在一般Petri网中，对递归的描述非常困难。实际应用π演算时递归结构经常出现，因此，本文给出了一种π演算中递归结构转换为Petri网的方法。

1 基本概念及转换规则

1.1 基本概念

关于π演算的基本概念，在文献［3］中已有详细介绍在此不再赘述。在给出π演算中递归表达式基本形式之前，先看一个例子：

式（1）中每个通道a、b、c、…中都保存着一个数值h′（这个数值可以不一样），从已知通道a开始，读取通道内当前值h′加到现有的值上，直到得到的h值大于10时可以选择执行输出该值。这样，从a开始到输出h时所有计算过的通道即是该get函数的路径。

在式（1）中，既有自调用的算子，又有非自调用的算子，并且有选择运算符“＋”将两个进程相连。在不满足递归出口条件时，多次执行前缀算子ab获取下一个通道，并执行计算h值操作。当满足递归出口条件时，可以选择继续自调用，也可以终止调用过程。

本文给出了一种一般π演算的递归表达式的基本形式：

当然，在一些表达式中也会出现有多个自调用表达式的形式，比如：

在式（3）至式（5）中，均有两次自调用，虽然在转换时与式（2）有点不同，但基本转换思路大致相同。为了方便描述转换过程，在本文中，以式（2）这种递归形式为例。

为了更好地记录递归运算的层次，本文引入轨迹的概念。通常，轨迹一般用来指进程P所依次执行的一系列活动，一般用〈action1，action2…〉表示。

定义1 轨迹：π演算递归结构执行时，为了记录递归运算的层次，我们将递归调用的顺序称为轨迹，用字母trail表示。调用一次用σ1表示，调用第二次用σ2表示，以此类推，调用第n次用σn表示，则进程中递归结构执行的轨迹trail＝〈σ1，σ2，…，σn〉。

定义2 逆轨迹：与轨迹相应地，在递归返回时其轨迹称为逆轨迹，记为trail－1，上述递归返回的逆轨迹即为trail－1＝〈σn，σn－1，…，σ1〉。

在本文中，π演算进程P转换而成的Petri网记为NP，NP是一个有向连通图，其节点分别称为库所和变迁。这些节点通过有向弧相连。相同类型的两个节点之间是不允许相连的。

1.2 转换规则

递归π演算向Petri网转换要遵循一些转换规则，在本文中将这些规则概括为两类：基本进程的转换规则以及组合规则。

1.2.1 基本进程转换规则

对于向子网K（ρ）的转换，是根据表达式ρ的语法树，其组成为给定基本子项（进程项0，进程调用，内部动作以及输入输出前缀）的图转换。

由于不涉及任何的名字操作，因此进步进程项0和内部动作前缀τ十分简单。进程调用X（α1，…，αnX）也类似，但是结果将产生一个层次变迁，它将通过标识等价规则进行激发变换［10］。

具体的转换规则如图1所示。

图1 空进程、哑动作τ、进程调用、动作前缀向Petri网转换规则Fig.1 Translation rules from o，τ，the process call and the prefix to Petri nets

1.2.2 组合规则

本节中的组合规则用于合并Petri网的算子，包括前缀组合规则、选择组合规则、并行组合规则以及范围处理规则，其中前3个规则给出了合并标签库所、相应的持有者的方法［12］。

假设有网Ni＝（∪，Ti，ιi）（i＝1，2）是两个不相干的未标记的Petri网，并且有∀s1，s1∈，∀s2，s2∈，如果ι1（s1）＝（λ，D1），ι2（s2）＝（λ，D2），那么D1＝D2，即被相同符号标识的持有者库所也有同样的值类型集合。下面将给出四种组合规则的形式化处理方法，如图2所示。前缀组合规则：N1.N2。假设N1有唯一的入口控制库所和唯一的出口控制库所（出口控制库所记作s1），通过如下步骤获得组合结果：

（1）网N1和网N2并排放置。

（2）对应每个s2∈°N2，创建一个新的库所s′2，用符号i标识，同时将网N1和网N2中在si和t∈Ti（i∈｛1，2｝）的弧Ψ在新的库所s′2和t上标记，并使用同样的注释符号和同样的弧类型（无向或是有向的）标记，而后网N1的唯一出口控制库所和网N2的出口控制库所将被删除。

（3）对于有相同标识符号和类型的持有者库所将被合并为一个持有者库所，并且如前一样，具有相同的标识符号和类型，在原来的网N1和网N2中连接合并的持有者库所与变迁之间的弧及注释标识在合并后的持有者库所中保持不变。

1）选择组合规则：N1＋N2，可通过如下过程获得图转换结果：

①网N1和网N2并排放置。

对于每个s1∈°N1和s2∈°N2，创建一个新的库所s，用符号e标识，并且使得每个在si和t∈Ti，i∈｛1，2｝的弧Ψ在新的库所s和变迁t上作同样标识，即使用相同的注释符号和相同的弧类型（无向或是有向的）；类似地，对于每个s1∈和s2∈，创建一个新的库所s，用符号x标识，其连接性与上面规则定义一致。最后，将原来在网N1和网N2中标识的入口控制库所（被符号e标识）和出口控制库所（被符号x标识）删除。

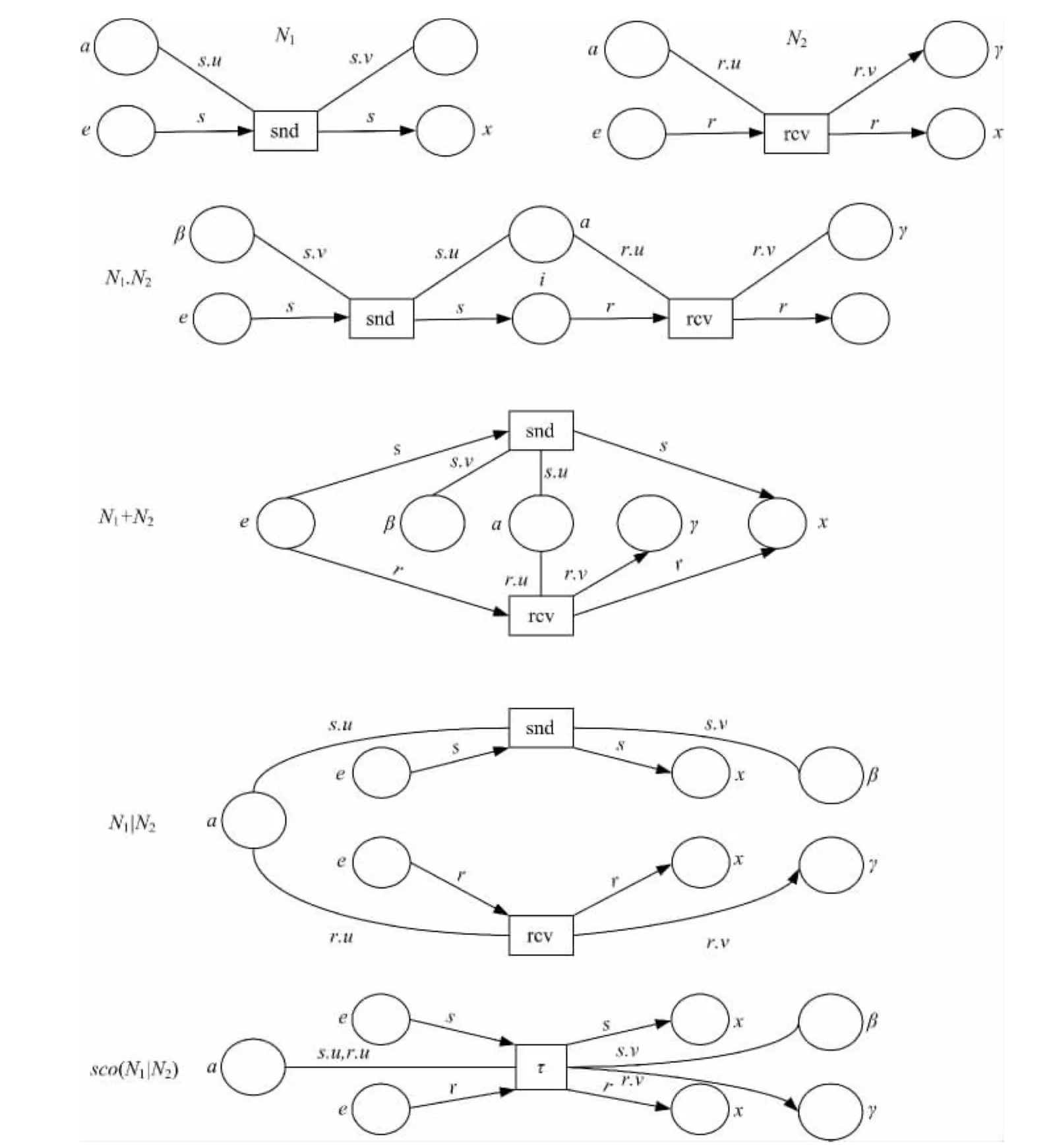
图2 组合规则Fig.2 Composition rules

②具有相同名字的持有者库所的合并可参见前缀组合规则。

2）并行组合规则：N1｜N2，可通过如下过程获得图转换结果：

①网N1和网N2并排放置；

②具有相同名字的持有者库所的合并可参见前缀组合规则。

3）范围处理规则：N＝sco（N1），可通过如下过程获得图转换结果：

①对于每对变迁t1，t2∈T1，其中t1和t2分别被snd或rcv所标识，创建一个新的变迁t，用符号τ标识，而在变迁t与库所s上的弧注释符号是在变迁t1与库所s以及变迁t2与库所s的弧注释符号的简单合并。在这里注意在snd所标识的变迁周围的弧与rcv所标识的变迁周围的弧是互不相干的，所以不需要进行反复的合并操作。

②最后删除被snd和rcv所标识的变迁以及与其相连接的弧。

2 递归π演算向Petri网的转换及等价性证明

2.1 准备与讨论

类似于式（1）中的例子，当数据h满足h＞10时才可以选择执行h.0，因此在执行递归时要判断是否满足递归出口的条件。因此在递归调用和递归返回间加入一个判定库所，用来存储判定是否满足递归出口条件的判定托肯。判定托肯的形式为F.D或者T.D，其中F.D表示不满足递归出口条件，D表示这个托肯的类型是判定托肯（decision token）；T.D表示满足递归出口条件。

对于如何记录当前数据属于哪次递归操作，本文采用trail.data.place的形式，即当前轨迹.数据值.所在库所的形式存储在栈库所中。

对于轨迹，在执行递归调用时，调用一次用σ1标记，调用第二次用σ2标记，…，调用第n次用σn表示，进程中递归结构执行的轨迹trail＝〈σ1，σ2，…，σn〉。例如递归主体X（a1，…，an）将用轨迹标记为σ1，σ2，…，σn.X（a1，…，an）。对于递归主体后面的Q（a″1，…，a″n），在递归返回之前是不执行的，在执行Q（a″1，…，a″n）时是按照轨迹〈σ1，σ2，…，σn〉的逆轨迹〈σn，σn－1，…，σ1〉执行的。

2.2 递归π演算向Petri网的转换

对于π演算递归结构向Petri网的转换，本文采用层次化方法，即将表达式中的每一个子表达式（包括递归主体）都先转换成对应的子网，然后组合起来；如果自调用表达式没有满足递归出口条件，那么对自调用表达式的网结构进行进一步细化，将下一次调用的网结构展开代替上一层中自调用表达式对应的网结构。

下面给出关于式（2）的递归结构全景图第一层，如图3所示。

说明：

（1）最开始的库所e与最后的库所x是此π演算表达式对应网结构的控制库所，这是假设该表达式是一个主式；如果此递归π演算表达式是其他π演算表达式的子式，这两个库所应换成与外界相连、用于传递控制信号的内部库所i。

图3 典型π演算递归结构转换结果全景图第一层Fig.3 First layer of franslation panoramic view from typical recursionπcalculus to Petri net

（2）图中的库所d是本文新加库所——判定库所，存储了判定是否满足递归出口条件的判定托肯F.D和T.D。

（3）在自调用表达式对应的网结构与判定库所d之间有一条弧相连，表示在执行自调用表达式时，其中的条件发生了变化，这个变化的条件要及时传给判定库所，使判定库所做出合理的判断。

（4）在P（a1，…，an）、Q（a″1，…，a″n）等表达式前进行了轨迹的标记；而表达式R（b1，…，bn）却没有轨迹标记，因为在递归调用时此表达式只执行一次。

（5）判定库所对应一个判断逻辑，严格来讲，如果系统中有多个递归表达式，则每一个表达式单独对应一个判定库所。

（6）出于版面考虑，这里没有画出栈库所、名字持有者库所、标签库所以及相关弧。

式（2）递归结构全景的第二层如图4所示。

图4 典型π演算递归结构转换结果全景图第二层Fig.4 Second layer of translation panoramic view from typical recursionπcalculus to Petri net

类似地，调用多次的π演算表达式对应的网结构也能够给出。

对于形如式（2）的π演算表达式，采用层次化方法，将π演算递归结构转换成Petri网的步骤为：

（1）按照1.2节中的基本进程转换规则及组合规则将P（a1，…，an）、R（b1，…，bn）以及Q（a″1，…，a″n）分别转换成对应的子网NP1、NP2、NP3。

（2）将自调用表达式X（a′1，…，a′n）先看做一个整体表示，对应的网结构先用NP0表示。各个组成部分用构造sco（NP1｜NP2｜NP3｜NP0）网连接起来，这将多种标签库所和可能来自不同部分的有uv和v标记的变迁对合并起来。这个构造并不合并其他的持有者库所。移除所有标记为uv和u－v的变迁。

（3）判断X（a′1，…，a′n）是否满足递归出口条件，若不满足，将X（a′1，…，a′n）视为X（a1，…，an），转步骤（1）。用不同的标记来记录不同的调用；若满足，转（4）。

（4）将图3中的变迁P（a1，…，an）用子网NP1替换，如果NP1只有一个输入库所e，那么将此库所与开始的库所e合并，仍旧记为e；否则创建一个辅助变迁t1，使开始库所e指向辅助变迁t1，然后由变迁t1指向NP1所有的输入库所e，再将NP1所有的输入库所e改为内部库所i。

同样地，如果NP1只有一个输出库所x，将此库所与最后库所x合并，记为x；否则创建一个辅助变迁t2，使NP1所有的输出库所x指向辅助变迁t2，然后由变迁t2指向最后的库所x，再将NP1所有的输出库所x改为内部库所i。

在用NP2、NP3替换R（b1，…，bn）、Q（a″1，…，a″n）时也做同样的处理。

（5）将相同的名字持有者库所合并，与原库所相连的弧以原方式练到合并后的库所上。将需要保存数据的变迁用弧与栈库所相连。

（6）为了得到完整的变迁网NP，向输入库所中插入一个小黑点作为托肯，并把下面的通道插入到持有者库所中去：

①把ζ（α）插入到每个α标记的持有者库所中，其中α∈domain（ζ）；

②把a.a.K插入到标签库所中，其中对于每一个a∈konwn（ζ）；

③把n.N插入到标签库所中，其中n∈C＼konwn（ζ）；

④把Δ.R插入到标签库所中，其中Δ∈rstr（ζ）。

2.3 互模拟等价

本文定义了从递归π演算到Petri网的语义转换，从而产生了有限结构转换网——NP，它是具有有限库所、变迁和弧的网结构，该递归结构的标号迁移系统ItsP与转换后的Petri网所对应的标号迁移系统ItsNp是强互模拟。

定理1 NP是具有有限库所、变迁和弧的Petri网图，并且使得ItsP和ItsNp是互为强互模拟的标号迁移系统。

证明 基本π演算部分的Petri网语义等价证明在文献［12］中详细介绍了转换的思想、方法以及相关的语义等价证明，在此不再赘述。

关于递归结构的Petri网语义等价的证明采用数学归纳法。具体如下：

设K为递归结构执行次数，即递归层数。

（1）当K＝1时，按照文中所述递归π演算向Petri网的转换方法，其直接转换为不带递归结构的基本π演算，其互模拟等价性是已知的。

（2）假设当K＝n时，从递归π演算向Petri网的转换具有互模拟等价性，那么证明当K＝n＋1时互模拟等价仍成立。由于当K＝n时，前n层的递归调用已经实现，即可以将前n层递归调用得到的π演算表达式看做一个复杂无递归的基本π演算表达式，这样再加上第n＋1层的递归调用转化为（1）中的形式，此时K′＝1，符合（1）中所证互模拟等价。因此当K＝n＋1时递归π演算向Petri网转化的互模拟等价性成立。证毕。

对不同密度、不同施肥处理的相对增加量进行双因素方差分析，结果表明(表5)：3种不同施肥处理并未对毛竹相对增产量产生显著差异(P=0.138>0.05)；在试验所设2种密度中，低密度毛竹林相对增加产量显著高于高密度毛竹林(P=0.023<0.05)。

3 更简洁的Petri网表示

Petri网是一个很好的描述与分析并行系统的模型。但是当递归结构递归的次数较多时，会产生巨大的Petri网。尤其是在实际应用中，如果系统过大或较复杂时，会遇到结点数过多的情况。系统的组合状态数又随结点数成指数函数增长，这就是所谓的组合爆炸问题。解决结点数过多引起的组合爆炸问题的办法是尽量减少模型的结点个数。为了使转换后的Petri网较为简洁，本文给出了压缩的Petri网图，它保留了系统的语义，并编码完全相同的轨迹集合。

3.1 一种更简洁的Petri网表示

分析如式（2）形式的π演算的递归结构，如果该π演算表达式不满足递归出口条件，那么会循环执行自调用表达式之前的子表达式P（a1，…，an），执行过程大致如图5所示。

如果π演算表达式的递归结构执行多次，那么会产生巨大的Petri网，因此本文考虑将其进行简化，得到一种更简洁的Petri网表示。受图3启发，本文将典型π演算递归结构转换结果用全景图表示，如图6所示。

这里需要考虑以下几个问题：

图5 π演算表达式递归结构执行图Fig.5 Execution ofπcalculus expression recursive structure

图6 一种更简洁的Petri网表示Fig.6 A more compact representation of Petri net

对于递归出口之前每次执行的表达式P（a1，…，an），其每次具体执行是不一样的，我们在其前面用轨迹标记，表示按照轨迹σ1，σ2，…，σn执行，这里的轨迹是根据判定库所的变化一步一步生成的。然后在执行递归返回时，Q（a″1，…，a″n）按照轨迹σ1，σ2，…，σn的逆轨迹σn，σn－1，…，σ1执行。

3.2 等价性证明

本文给出了Np的一种更简洁Petri网表示，记为Nc，它是具有有限库所、变迁和弧的网结构，保留了系统的语义，编码完全相同的轨迹集合。

定理2 Nc是具有有限库所、变迁和弧的Petri网图，并且使得Np和Nc编码完全相同的轨迹集合（激发顺序）。

证明 针对递归结构，分别从递归调用、递归出口及递归返回三部分考虑其执行的轨迹集合。

（1）对每次递归调用执行的表达式P（a1，…，an），Np和Nc的执行轨迹均为｛σ1，σ2，…，σn｝。

（2）对递归出口执行的表达式R（b1，…，bn），由于只执行一次，因此其轨迹集合可以忽略。

（3）对递归返回表达式Q（a″1，…，a″n），Np和Nc的轨迹集合均为｛σn，σn－1，…，σ1｝。证毕。

4 结束语

通过对π演算递归结构和Petri网的经典理论进行研究分析，本文首先给出了递归π演算的基本形式，然后将递归π演算向Petri网进行转换，并证明这种转换的互模拟等价性；随后针对多次递归的情况对由π演算递归结构转换得到的Petri网进行简化，得到了一种保持系统语义的、编码完全相同的轨迹集合的更简洁的Petri网，与原Petri网相比能够提高对于模型验证的效率，比如对移动系统的验证等。

［1］Thomas E.Service-Oriented Architecture（SOA）：Concepts，Technology，and Design［M］.New Jersey：Prentice Hall，2005.

［2］Leymann F，Roller D，Schmidt M T.Web services and business process management［J］.IBM Systems Journal，2002，41（2）：198-211.

［3］Milner R，Parrow J，Walker D.A calculus of mobile processes part I／II［J］.Journal of Information and Computation，1992，100（1）：1-77.

［4］Milner R.Communication and Concurrent［M］. New Jersey：Pretice Hall，1989.

［5］Roland Meyer.A theory of structural stationarity in theπ-Calculus［J］.Acta Informatica，2009，46：87-137.

［6］Michele B，Davide S.A fully abstract semantics for causality in the Pi calculus［C］∥Proceedings of STACS＇95，LNCS，Springer，1995，900：243-254.

［7］Baeten J C M，Bergstra J A，Klop J W.An operational semantics for process algebra［J］.Mathematical Problems in Computation Theory，1988，21：47-81.

［8］Eile B，Raymond D，Maciei K.Petri Net Algebra［M］.Bolin：Springer，2001.

［9］Ulrich B，Daniel M.Object-oriented concepts for coloured Petri nets［C］∥IEEE International Conference on Systems，Man and Cybernetics，1993，3：279-286.

［10］Peschanski F，Klaudel H，Devillers R.A Petri Net Interpretation of Open Reconfigurable Systems［C］∥PETRI NETS 2011，LNCS 6709，2011：208-227.

［11］Christensen S，Hansen N D.Coloured Petri nets extended with place capacities，test arcs and inhibitor arcs［J］.Application and Theory of Petri Nets，1993，691：186-205.

［12］Raymond D，Hanna K，Maciej K.A compositional Petri net translation of general Pi calculus terms［J］. Formal Aspects of Computing，2008，20：429-450.

［13］Peschanski F，Klaudel H，Devillers R.A decidable characterization of a graphical pi-calculus with iterators［C］∥In：Infinity.EPTCS，2010，39：47-61.